基于潜标的入水冲击仿真研究
杨飞
(中国船舶集团第七一五研究所,浙江杭州 310000)
入水冲击问题是一种强非线性的物理问题。其涉及固体、液体、气体三者相互耦合作用,非常复杂,广泛地存在于工程应用之中,如鱼雷入水、救生艇抛落、飞机迫降等问题[1-5]。运用理论方法对入水冲击问题进行求解时,往往进行了简化处理,结果误差较大。而采用模型来进行缩比试验时,成本巨大,不便于进行广泛的推广研究。现如今,随着时代的日新月异的发展,计算机技术的更新迭代,使得采用计算机,运用有限元方法来求解结构入水问题成为可能。现阶段,采用有限元等方法来探究结构入水时的响应及运动规律已经得到了广泛的应用。国内外众多学者已经对入水冲击问题开展了数值研究分析[6-10]。
潜标在入水过程中,当其底部受到较大的冲击载荷时,会出现结构损坏,内部元器件失灵等诸多问题。本文采用STAR-CCM+ ,基于重叠网格,对潜标抛放时的入水冲击问题进行研究。
1 基本控制方程
本文采用的控制方程主要为连续性方程以及N-S方程。
1.1 连续性方程
连续性方程(质量守恒方程),可以通过质量守恒定律推出:

其中,ρ 为流体密度;t 为时间;u 为速度矢量。
1.2 N-S 方程
Navier-Stokes 方程,简称N-S 方程。具体描述为:外界对控制力以及控制面上所做上的力的总和,同该控制体内流体动量关于时间的变化率,以及单位时间内控制面的动量净流出量相等。由此可以推出N-S 方程:
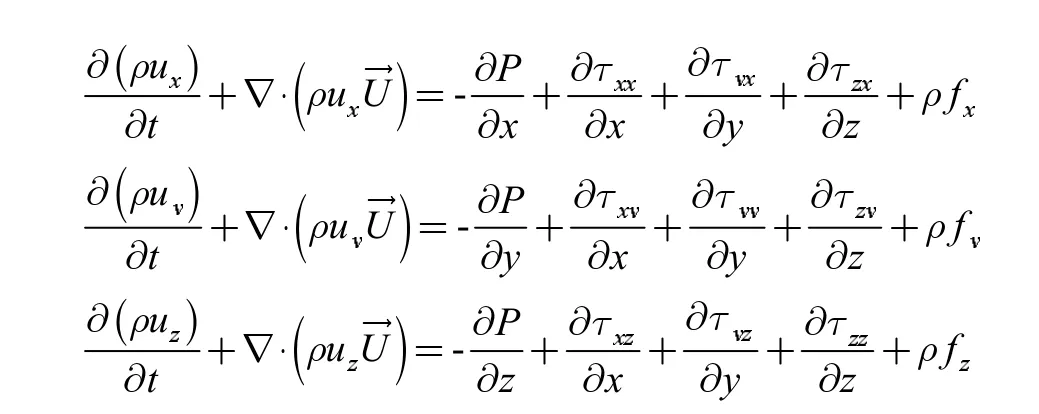
上面式子中,P 为作用于控制体上的压力,τxx、τxy、τxz分别为作用于控制体表面的粘性应力分量。fx、fy、fz则分别为单位质量力在x、y、z 方向上的分量。
2 有限元数值模拟
2.1 有限元模型建立
本次研究对象为某潜标,由于潜标与水面接触时,受到冲击载荷的作用发生在极短的时间内,因此可不考虑风浪流的影响,将海面近似等效为平面。由于着重研究潜标入水时外表面所受到的冲击载荷,为了节省计算量,提高计算效率,对潜标进行了相应的简化。图1 结构物以20°入水时的有限元模型。

图1 潜标20°入水时的有限元模型
2.2 网格划分
基于star-ccm,采用重叠网格对潜标进行了网格划分工作,由于需要重点观察潜标自由面的液面状态,故对自由面的附近进行了网格加密处理。同时为了进一步优化计算,因此需要简化网格,减少网格数量,对潜标入水过程的垂向网格也进行加密处理。网格数目约为250万左右。
2.3 边界条件
边界条件的设置如下:
对于结构件,默认为刚性体,故其边界条件选择固壁面边界条件。在六自由度运动条件中设置潜标的运动,给出重量、重心、转动惯量、初始速度等一系列条件。背景域的入口选择速度进口,上下表面同样选择速度进口,出口选择压力出口,为了减弱边界效应,背景域两侧选择对称平面。
2.4 其他设置
物理模型:为了便于观察自由液面,故选取多相流模型,选取空气及水作为多相流的介质,并在VOF 波中建立波浪模型并设置静水面的参数。为了精确地模拟潜标在多相流中的运动,选择不定常k-ε 湍流模型来进行计算。
3 仿真结果分析
根据实际测量,分析了潜标入水角度为0 度到20 度(以海平面为基准,同海平面平行为90 度),入水速度为5m/s、10m/s、15m/s。
3.1 不同速度下的潜标入水冲击载荷特性
分析了潜标基于相同角度下,以不同的速度冲击水面时,速度对其冲击水面时入水载荷的影响,本文研究了入水冲击速度分别为5m/s、10m/s、15m/s 时潜标的底部所受的冲击载荷,得到的底部压力曲线图如图2 至图4 所示。从图中可以看出,各种入水角度下,潜标在不同速度下冲击水面的底部压力曲线大体相似。当潜标撞击水面时,即潜标同水面接触的初期,潜标的底部所受到的冲击载荷压力在较短时间内急速增大至峰值,该峰值仅仅出现于潜标冲击水面的瞬间, 而后随着潜标入水深度的增加,该峰值迅速减小,而后潜标所受冲击压力值慢慢减小至较小值,且在较小值的附近来回不断震荡。从对比图中可以看出,潜标入水的速度同其到达压力峰值所需的时间成反比,同震荡稳定所需要的的压力值成正比,即入水的速度越大,到达峰值所需的时间越短,震荡稳定时所需要的载荷也就越大。不同的地方是,当潜标以较大速度冲击水面,其底部压力峰值随着速度的增大而增加,且压力峰值随着速度的改变而变化,当入水角从0°缓慢增加到10°时,峰值变化较少,但潜标入水的角度从10°增加到20°时,压力峰值迅速减小。
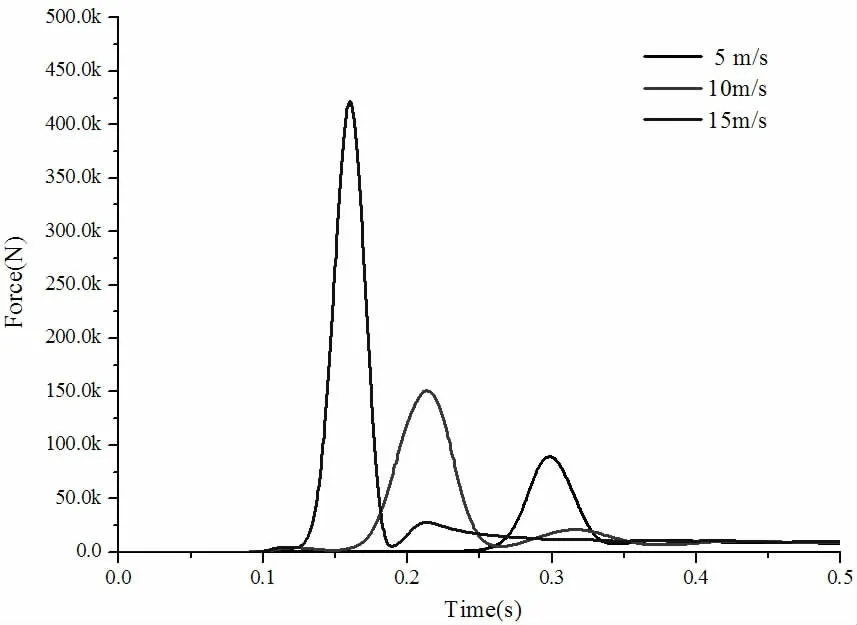
图2 入水角为0°时不同速度下潜标底部压力对比曲线

图3 入水角为10°时不同速度下潜标底部压力对比曲线
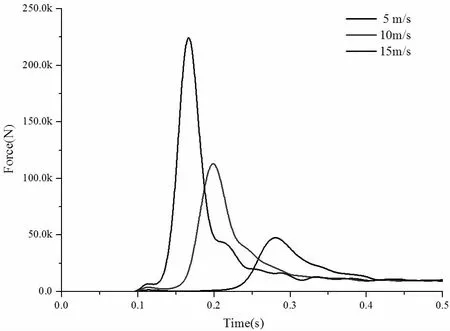
图4 入水角为20°时不同速度下潜标底部压力对比曲线
3.2 不同角度下的潜标的入水冲击载荷特性
为了分析不同入水角对潜标的影响,分别研究了相同速度下,不同角度对潜标入水砰击的影响,得出的冲击压力曲线如图5-7 所示。

图5 速度为5m/s 时不同角度下潜标底部压力曲线图

图6 速度为10m/s 时不同角度下潜标底部压力曲线图
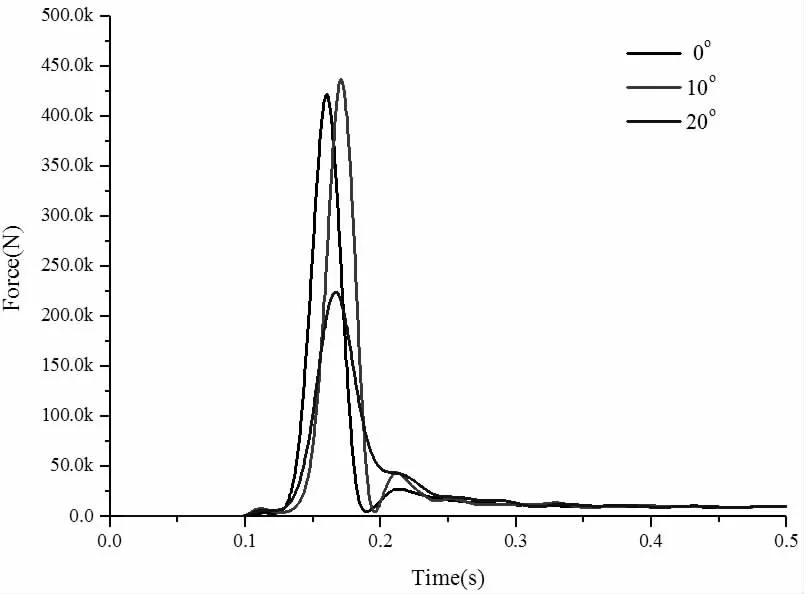
图7 速度为15m/s 时不同角度下潜标底部压力曲线图
分析了潜标以相同的速度入水时,入水时的角度对其冲击水面时所受的入水载荷的影响。分别研究了潜标的入水角度在0°、10°、20°时,潜标底部所受的冲击载荷。得到的底部压力时历曲线图如图5 至图7 所示。从图中可以看出,三张图规律大体相似,潜标冲击水面时,峰值压力变化规律相似,先迅速增加至最大值,而后迅速衰减,在一个较小值附近不断震荡。当潜标入水的速度增大时,其底部所受到的冲击压力峰值也进一步增大。但其到达峰值所需要的时间随着速度的增大而减小。当入水角度从0°逐渐增大的过程中,从时历曲线图中可以发现,底部冲击压力的峰值随着入水角的增大先增大后减小,其在20°入水时的峰值约为10°入水时峰值的一半。
因此,综合来看,在设计抛放角度及速度时,应尽量选择较小速度,倾斜角度在20°左右时入水,能够极大地减少潜标入水时所受到的冲击载荷。
4 结论
本文采用STAR-CCM+软件分析了潜标以不同角度、不同速度入水冲击的过程,得到了潜标的底部冲击压力变化时历曲线图。对仿真的结果进行了总结分析归纳,得到了以下规律:
4.1 潜标在入水时,其底部所受冲击压力迅速增大至峰值,而后峰值迅速衰减,保持在一个较低的水平,且在较小值附近不断震荡。
4.2 在入水的角度相同的情况下,潜标到达峰值所需要的时间同其入水时的速度呈反比,即当潜标入水时的速度越大,其所受载荷到达峰值所需要的时间也就越短,震荡稳定所需要的载荷也就越大。
4.3 在入水角度相同的情况下,潜标在入水冲击时所受压力的峰值同入水速度呈正比,压力峰值随着入水速度的增加而增大。
4.4 在入水速度相同的情况下,潜标入水所受的峰值压力随着入水角度的增加先增大后减小。
4.5 在选择设计潜标入水速度及入水角度时,应尽可能选择较低的速度,使倾斜角度在20°左右时抛放,能够有效得减少潜标入水时所受到的冲击载荷。

