线性时变作战系统运用效能评估方法*

毛腾蛟，张东戈，牛彦杰，禹明刚，何 明

（1.陆军工程大学指挥控制工程学院，南京 210007；2.军事科学院，北京 100091）

0 引言

战场上作战系统的运用效能，不仅与人员操作有关，还与作战系统内部所含装备的性能状态有关。随着作战进程在时间上的推进，人员操作的有效性、装备性能状态都会发生改变。为了研究人员操作和装备性能状态变化对作战系统运用效能的影响，需要构造一个时变影响关系模型。

目前，作战系统效能研究的主要方法有美国工业武器系统效能咨询委员会提出的系统效能模型（availability dependability and capability，ADC）、杜佩（Dupuy）的理论杀伤力指数及层次分析法（analytic hierarchy process，AHP）、模糊综合评判法（fuzzy comprehensive evaluation，FCE）和专家评判法（expert evaluation method）等。除了一般方法之外，TANG H等着重分析了人员操作对作战系统效能的影响；ZHANG S T 等研究了战场环境对作战系统效能的影响；GU L 用价值函数评估武器系统效能。

随着战场上武器装备的多样化、信息化、智能化发展，研究人员就具体装备和特定情形下的系统效能评估进行了研究。面对单一方法评估模型的局限性，AGUS S W 等提出多模型综合评估作战系统效能。随着人工智能领域的发展，有学者基于大数据、神经网络等研究了系统效能评估问题。

综合来看，目前作战运用效能评估分析方法中，使用宏观统计分析的方法较多，采用要素分解法进行解析分析研究较少。毛腾蛟等研究发现，将时域特性转换为频域特性，是一种有效的方法，它可以分要素地考察人员操作和战场因素对作战效能的影响，这对于信息化战场中的系统要素影响力分析，有方法学意义。

1 模型构建

作战系统是指人员与武器装备结合并能够独立完成一定任务的综合性整体。极端精简的情形是一名士兵配备单兵作战武器构成的作战系统。更复杂的作战系统，可以是包含所有操作人员和武器系统的一辆运行中的坦克。凡是依靠人员操作和武器装备系统结合来形成和输出效能的系统，都在本文的研究范围之内。一群持有同样武器装备的松耦合单兵，不是本文研究的对象。

作战系统的运用效能，既与作战人员的操作有关，也和武器装备的性能状态有关。为研究它们之间的影响关系，将人员对武器装备的操作作为模型的输入，装备的性能状态作为模型的系统响应函数，作战系统的运用效能作为模型的输出。其逻辑关系框架如图1 所示。根据作战系统的特性，可以提出如下模型假设。假设1 模型的因果性假设：只有在作战人员对系统进行操作后，作战系统才会输出产生运用效能。某时刻的操作，会对未来一段时间的输出产生影响。

图1 作战系统运用效能关系

假设2 模型的齐次性假设：为了简化分析，对于同一类型的操作，当操作的人数提升一定倍数时，输出的运用效能也提升相应的倍数。即若用x 表示系统的输入，y（x）表示输出，假设2 可以描述为y（ax）=ay（x）。

若一名作战人员操作装备A 会使系统输出换算为a 的运用效能，则n 名作战人员同时操作装备A 会使系统输出换算为n·a 的运用效能。比如，两个装填手，是一个装填手效能的两倍。

假设3 模型的叠加性假设：对于不同类型的操作，作战人员同时进行操作时的总体输出运用效能与分别操作输出的运用效能的叠加等效。即，若用x、x表示系统不同类型的输入，y（x）表示输出。假设3 可以表示为y（x+x）=y（x）+y（x）。

若一名作战人员操作装备A 会使系统输出换算为a 的运用效能，另一名作战人员操作装备B 会使系统输出换算为b 的运用效能，则如果两人同时对装备A、B 进行同样的操作，系统换算输出运用效能为a+b。这种假设没有考虑影响权重，是出于简化模型分析的考虑，考虑影响权重，虽然更贴近实际，但是会复杂化问题的模型化分析，损害方法学研究清晰化的要求。

还需要说的是，本文所提出的齐次性和叠加性假设针对的是不同操作组合对作战系统运用效能的解析化影响，不同于战斗力与兵力数量宏观统计层面的关系研究。本文所研究的作战系统模型，符合线性系统特性。

由于作战系统中装备性能状态会随着作战的延续而改变，即使在不同的时间阶段进行相同的操作，由于装备性能状态的不同，作战系统会发挥出不同的运用效能。作战系统满足时变系统特性，可以用线性时变系统对其进行刻画。

1.1 人员操作的解析化描述

作战人员对系统的操作，是模型的输入，不同的操作输入将会产生不同的运用效能输出。人员操作的规范性和正确性，影响系统的效能发挥。

为便于理解，以极端简化的枪械操作为例进行说明。首先，操作人员不进行任何操作，枪械就没有任何操作效能输出。当操作人员对枪械进行“抡、劈”等操作，步枪发挥的效能与木棒发挥的效能相似。只有操作人员正确地装弹、据枪、瞄准、射击，才能使枪械发挥出其运用效能。

对于更复杂的作战系统，操作涵盖了多类操作人员，每类操作人员又担负着多种类型的操作。为方便研究，对作战系统的复杂操作进行分解，分解为由单一人员控制的基础简单操作。本文通过归纳战场上人员基础简单操作的特性，加入以下假设来进行近似简化。

假设4 基础简单操作的周期性假设：每项基础简单操作都具有固定的操作周期频率，不同的基础简单操作具有不同的操作周期频率。

将人员操作看成是周期性活动，或者是用周期性活动来进行刻画，是以人类行为为基础的作战问题分析的一种一般化方法。

基础简单操作的固定周期频率与作战系统中装备的设计参数有关。例如，根据作战系统装备的设计参数，炮手操作监视设备扫视一遍战场需要1 min，而装填一发弹药需要30 s。那么扫视战场的基础简单操作频率为1 次/min，装填弹药的基础简单操作频率为2 次/min。因此，可以用频率w代表标号为n 的基础简单操作。对于某一项基础简单操作，在不同的时间，人员的操作状态不同。本文用函数cos（wt）来刻画基础简单操作w在时刻t 的操作状态。当w=0 时，cos（wt）不随时间变化。可以用“w=0”表示始终保持一个固定状态的基础简单操作。例如，战场静默，即可用这一状态来表示。

假设5 基础简单操作的独立性假设：对于每一种基础简单操作，都有其独立的操作有效性。

例如，当炮手A 按照标准的操作规程扫视一遍战场可以发现10 个敌方目标，而炮手B 未按照标准操作规程，用同样的设备扫视同样的战场，只能发现3 个敌方目标，就称炮手A 比炮手B 的操作更有效。为衡量操作的有效性，定义参数c（t）为标号n 的基础简单操作在t 时刻的有效性指标。

有效性指标c（t）为一个相对的参数，设定c（t）∈［0，1］，操作越有效，c（t）的值就越大。当c（t）=1 时，代表了标号n 的基础简单操作始终按照标准操作规程，操作最为有效；当c（t）=0 时，代表这一基础简单操作最无效，完全不能发挥出作用。

战场上，人员疲惫会影响操作的有效性。因此，通常作战人员不能始终保持相同程度的准确和规范的操作。通常情况下，随着作战进程的持续延长，作战人员操作的有效性也会随之降低。由此可以设定c（t）是一个单调递减的函数，此时c（t）的时间导数c'（t）＜0。

据此，标号为n 的基础简单操作随时间的变化情况可以刻画为解析式c（t）cos（wt）。

根据假设2 和假设3，由不同类别基础简单操作的叠加合成，可以描述更为复杂的操作。例如，按照作战人员职责分工不同，作战人员对坦克进行的复杂操作由驾驶员的驾驶操作、车长的指挥和通联操作、炮手的火控操作等叠加合成。不同作战人员的操作还可以由更加基础简单的操作叠加合成，而这些基础简单操作，均具有假设4 的固定操作周期和假设5 的操作独立性等特性。

若复杂的操作包含N 种基础简单操作，那么复杂的操作可以刻画为：

将式（1）作为模型的输入操作信号。

1.2 装备性能状态的解析化描述

即使人员的操作相同，装备性能状态的差异也会影响作战系统的效能发挥。在这里，武器装备的性能指在制造完成后所具有的理论指标参数。

例如一辆坦克在制造完成后其设计的理论行驶速度、射速、射程、装甲防护厚度等参数都能反映其性能。武器装备在战场上长时间的操作或者对抗，都会造成性能的改变，武器装备通常不能始终维持于理论设计的指标参数，需要用实际的指标参数描述武器装备的状态。例如，坦克在战场上的时速、射程才真正反映了坦克的状态。通常随着战斗时间的延长，作战系统中武器装备的性能状态都会逐渐降低。

作战系统内能够体现装备性能状态的指标参数有很多，互相之间的影响关系比较复杂。对作战系统进行理想化操作，作战系统发挥出的效能就可以在一定程度上衡量装备的性能状态好坏。

如果将一辆自行车比为一个作战系统，对其操作为脚踩踏板一周，其输出的效能为向前滑行。若其性能状态良好，自行车可以滑行20 m；若其性能状态不佳，相同条件下只能滑行10 m。那么就可以用滑行距离衡量自行车性能状态的相对好坏。

评估作战系统装备性能状态，对其进行的理想化操作需要满足以下条件：1）为了全面评估系统，操作需要涉及作战系统中所有的装备。2）所有操作均按照标准规范进行。理想化操作就是对作战系统全员全装在最高标准下进行标准化操作。

根据假设1～假设5，可以使用不同的频率，来刻画这些不同的基础简单操作。理想化的操作用数学语言来描述，就是时域里一个包含全部频率分量的单位冲击函数。

单位冲击函数δ（t）的特性为当t=0 时，δ（t）=∞；当t≠0 时，δ（t）=0。经由傅里叶变换分解，单位冲激函数的频域特征为：

其图像表示如图2 所示。

图2 单位冲激函数的频域特征图

图2 中，单位冲击函数δ（t）包含了全部频率的分量，且各频率的幅值均为1，因此，它可以反映所有要素分量均进行理想化操作的情况，即全员全装的满负荷理想化操作。

假设某作战系统，输入一个单位冲击函数δ（t）后，其系统输出的效能如图3 所示。

图3 单位冲激函数的输出效能图

图中的输出运用效能曲线，可以用系统响应函数h（t）表示，作为装备性能状态的衡量指标。

假设6 当作战系统中装备有性能衰减时，随着时间推移运用效能输出会有成比例的下降，此时的装备性能状态，将会变化为σ·h（t）。其中，σ定义为衰减因子，表示在第m 个时段内装备性能的衰减程度。σ∈［0，1］，装备的性能衰减程度越大，σ的值越小。同时，操作使用时间越长，装备的衰减越大，也即m 越大，σ越小。如图4 中红色曲线所示。

图4 有衰减的系统响应函数图

由此，用σ·h（t）描述考虑现实影响后，在特定时段内装备性能的状态，并将其作为模型的系统响应函数。

2 运用效能的解析化分析

在战场上，装备性能状态的改变通常比较缓慢，由此可以认为，在较长的一段时间内衰减因子σ不会发生明显变化。根据这个特性，本文采用冻结系数法，分时间段地把作战系统看成为线性时不变系统进行研究。

作战人员对系统进行的复杂操作刻画为f（t），假设在时间（0，t）内操作时，系统响应函数σh（t）保持不变。若人员每隔Δ 时间进行一次操作，第n 次的输入操作可以描述为：

示意关系如图5 所示。

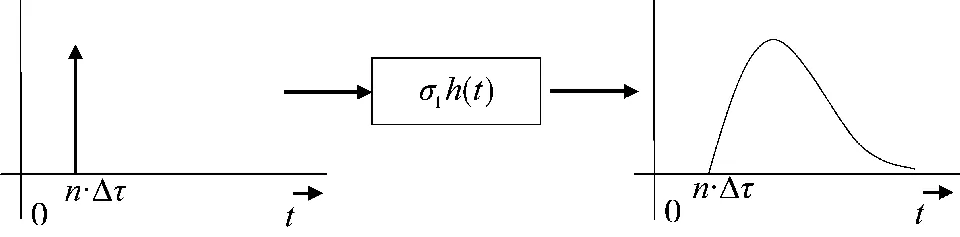
图5 第n 次操作的输出效能

在时间（0，t）内，作战人员的所有N 个输入操作可以表示为：

其关系效果如图6 所示。

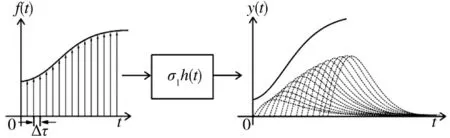
图6 时间区间（0，t1）全部操作输出效能

假设在（t，t）时间区间内，作战系统装备性能状态按照衰减因子影响下降。根据假设6，响应函数成比例下降至σh（t），（σ＜σ）。当输入为理想操作δ（t-t）时，其输出效能为σh（t-t）。第m 次操作发生在这段时间内，操作输出的效能为：

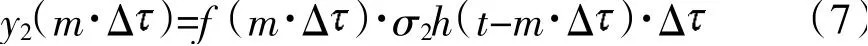
示意关系效果如图7 所示。

图7 第m 次操作的输出效能

在（t，t）时间区间内作战人员的所有M 个操作输入可以表示为：

示意关系效果如图8 所示。图中红色曲线表示装备性能状态改变后的输出。如果用来观察战场的时间切片足够大，观察时间足够长，相比起长时间的战场观察周期，人员操作的间隔时间就显得非常短，甚至可以忽略不计，因此，可以将人员的操作看成是连续的，此时操作间隔时间Δ 趋近于0。作为战场宏观规律探究，这一假设是合理的。由此，式（11）变为：

图8 全部操作的输出效能

式（12）为分时段卷积的函数关系式。在模型假设的基础上，可以扩展为普遍情况，按照装备性能状态的不同划分不同的时段，运用效能与人员操作和装备性能状态符合分时段卷积关系。

至此，作战系统的运用效能就可以用解析式y（t）量化描述。y（t）值的大小反映了作战系统运用效能的相对优劣。

转化为实际应用的时候，可以根据实际任务需求情况设计合适的效能阈值D。当y（t）＞D 时，表示作战系统的运用效能满足作战需求；当y（t）＜D 时，表示作战系统的运用效能不满足作战需求，以此来解析化评估作战系统的运用效能。

3 示例仿真计算检验

将某型坦克作为一个作战系统进行分析。设定其基础简单操作为防护、机动、搜索、装弹、瞄准和射击。根据这些操作的特性，可以分别用频率w=0、w=2、w=3、w=4、w=5、w=6 表示。当坦克的武器装备均无衰减时，根据坦克的理论指标参数，刻画其性能状态h（t），如图9 所示。

图9 无衰减的系统响应函数h（t）

由图可见，对坦克进行一次理想化操作，坦克的运用效能在未来一段时间内先上升，然后逐渐衰减。这和人们根据历史所总结出的实际作战经验相符。由假设6，根据坦克武器装备性能衰减的情况设置衰减因子σ。

3.1 操作有效性衰减对运用效能的影响分析

当在低强度的对抗中，若坦克内各作战人员操作有效性的变化程度相同，可设定各操作的有效性指标c（t）=c（t）=c（t）=c（t）= c（t）=c（t）=e，那么该坦克系统的输入操作信号为：

如图10 所示。

图10 f1（t）的输入操作信号

当在操作时间内装备性能状态没有发生变化，根据式（12）坦克输出的运用效能y（t），如下页图11所示。

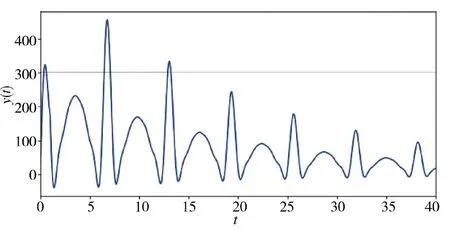
图11 作战系统输出运用效能y1（t）

设置效能阈值D=300。根据计算结果，当时间t＞13 时，坦克的输出效能将不能满足作战需求。

在高强度对抗中，坦克的输出效能y（t）如图12红色曲线所示。

图12 坦克输出运用效能y2（t）

根据计算，当时间t＞7 时，坦克的输出效能不能满足作战需求。对比低强度和高强度对抗中坦克内作战人员的有效性指标e和e，并计算作战系统的效能满足作战需求的时间。可以得出结论：当作战人员操作有效性发生下降时，作战系统输出运用效能也会逐渐降低，由于对抗强度的不同，作战人员操作有效性下降的快慢就不同。操作有效性下降得越慢，作战的运用效能满足作战需求的时间越长。

这一结论符合战场上的一般经验认识。当输出运用效能不满足效能阈值时，就需要对人员的操作进行强化、调整，以提高作战系统的运用效能。

本方法不仅能够量化衡量人员操作有效性变化对输出效能的影响，还可以改变各基础操作的有效性指标，具体探究不同基础操作对运用效能的影响，进而发现关键操作。针对性地强化相关作战人员的关键操作训练，能够提升人员对关键操作的有效性，以最小的操作训练成本实现系统整体运用效能的最大提升。

3.2 装备性能状态衰减对运用效能的影响分析

在低强度对抗中，设定各操作的有效性指标

如图13 所示。

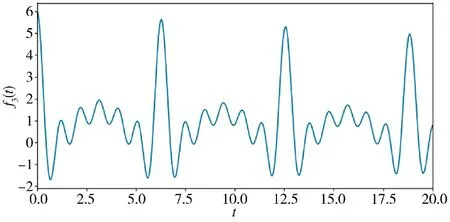
图13 f3（t）的输入操作信号

假设在时间区间（0，20），坦克的装备性能完好，当t=20 时，坦克由于受到打击，装备性能衰减。根据坦克受到打击的程度，设定以下几种情形。情形1：当坦克基本没有损伤时，装备性能状态衰减因子设定为0.9 时，操作输出的运用效能为y（t）；情形2：当坦克损伤较小时，装备性能状态衰减因子设定为0.8 时，操作输出的运用效能为y（t）；情形3：当坦克损伤较大时，装备性能状态衰减因子设定为0.7 时，操作输出的运用效能为y（t）；情形4：当坦克损伤特别大时，装备性能状态衰减因子设定为0.6 时，操作输出的运用效能为y（t）。装备性能状态对比情况如图14 所示。

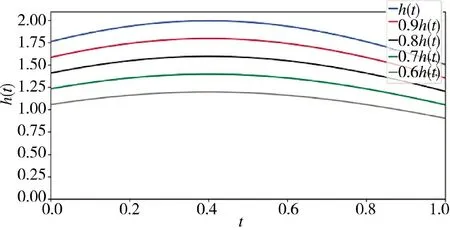
图14 不同衰减下的坦克装备性能状态

根据式（12），计算出的作战系统输出运用效能如下页图15 所示。

图15 中，y（t）为装备无性能衰减的输出运用效能。对比可以看出，在t=20 时在各情形中运用效能均有明显下降。衰减因子的值越小，输出的运用效能下降幅度越大。若仍然设置效能阈值D=300。当t＞20，情形4 的输出运用效能低于效能阈值D。由此可知：当坦克受到打击损伤特别大，装备性能状态衰减至原始装备性能状态的60 %时，坦克的输出效能将不能满足任务需求，需要对坦克的装备进行调整。

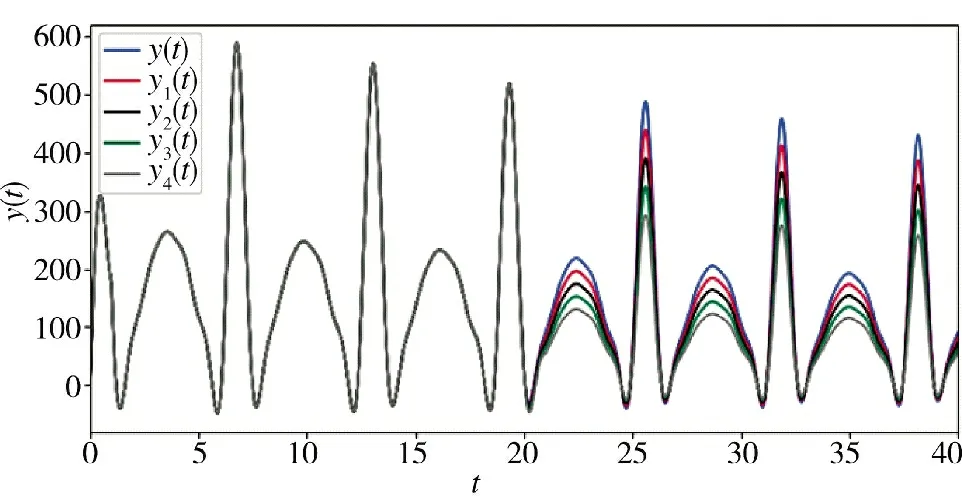
图15 不同衰减下作战系统输出运用效能

4 结论

通过归纳作战系统中人员操作和装备性能状态的特征，提出具有现实依据的假设条件，将实际的复杂系统进行简化，构建了线性时变作战系统运用效能的评估方法。推导出在线性时变作战系统中，运用效能与人员操作和装备性能状态，存在分时段卷积的关系。通过一个示例，计算出人员操作有效性的衰减和装备性能状态的改变对运用效能的影响，检验了方法的有效性。本文从理论上探索了一种新的系统效能分析方法，进一步能够为后续非线性复杂系统的分析研究提供思路。

为了保证方法的普适性，归纳了作战系统的一般特性，并未针对具体装备和特定作战场景进行研究。结合具体装备属性和作战环境，对模型的参数进行具体测定，对模型的相关细节进行补充。