基于贝叶斯优化LSTM 的发动机剩余寿命预测

张其霄，董 鹏，王科文，卢 苇

（海军工程大学管理工程与装备经济系，武汉 430033）

0 引言

航空发动机作为重要的航空装备，是一个十分复杂的系统，且航空发动机一般在高温、高压、高转速、高负荷等复杂条件下长时间运行，因此，保证航空发动机安全性和可靠性十分必要。其中，发动机的预测与健康管理（prognostics and health management，PHM）是一个有效的解决方案。剩余使用寿命（remaining useful life，RUL）预测是PHM 研究领域中的关键任务，目标是根据设备健康状态的数据，预测设备的剩余使用时间。航空发动机的剩余寿命预测主要方法可分为3 类：基于物理模型的预测方法、基于数据驱动的预测方法和混合预测方法。由于发动机结构复杂，难以建立精确的物理模型来进行描述，因此，基于发动机监控数据的数据驱动模型是有效的研究方法，成为众多学者们的研究热点。

基于数据驱动的RUL 预测方法不依赖于物理失效模型，而是基于数据分析和挖掘，提取反映系统健康状态的特征，继而借助于人工智能等算法实现剩余寿命预测。常见的数据驱动方法可分为两类：基于数理统计和基于机器学习的方法。典型的数理统计模型如马尔科夫、自回归移动平滑（AMRA）、维纳过程等。相较于统计模型，近年来，基于机器学习方法的研究与应用更为广泛，典型算法有人工神经网络、支持向量机、深度学习等。KHELIF等人基于支持向量回归（support vectorregerssion，SVR）对涡轮发动机进行了剩余寿命预测；也有学者利用多层感知机（multi-layerperceptron，MLP）进行剩余寿命预测的研究。现有的机器学习方法在一定程度上严重地依赖于专家经验，依靠人工来提取特征，在面对海量数据时性能一般。

深度学习是机器学习的一个组成部分，随着计算机性能的提升、数据积累和深度神经网络理论完善与发展，训练深层网络成为了一个重要发展方向。依赖深层网络提取特征和处理非线性表达，深度学习在许多传统机器学习难题领域取得了重大突破，但深度学习在健康评估和剩余寿命预测的应用仍在探索阶段。BABU G S 首先利用卷积神经网络（convolutional neural network，CNN）进行了剩余寿命预测。在LSTM 的应用中，ZHENG S 在2017 年首先利用LSTM 网络对涡轮发动机进行了剩余寿命预测；LI X 则利用LSTM 的变体BiLSTM 研究剩余寿命预测问题；李京峰运用深度置信网络对LSTM 进行优化，对涡轮发动机进行了剩余寿命预测；HE K则将（bidirectional handshaking LSTM，BHSLSTM）应用于剩余寿命预测研究。

虽然以上的几种深度学习方法在PHM 领域中已经有了一定的应用，但是在运用深度学习进行剩余寿命预测时，对超参数的确定主要根据经验或者手工优化，参数优化效率较低，在预测准确率上仍然有提升的空间。

因此，依据深度学习算法和优化算法，提出一种基于贝叶斯优化LSTM 模型的发动机剩余寿命预测方法。利用贝叶斯优化算法优化LSTM 网络，选择隐藏层数和初始学习率作为优化的超参数，将使用该组超参数在验证集上的RSME 作为目标函数。基于目标函数的过去评估结果建立替代函数找到最小化目标函数的值，并作为超参数。利用贝叶斯优化的LSTM 函数对发动机剩余寿命进行预测，利用NASA 数据集对方法进行验证。

1 基本算法

1.1 LSTM 算法

长短期记忆网络（long short term memory，LSTM）是循环神经网络（RNN）的变体之一，是针对RNN自身所存在的长期依赖问题和模型训练中存在梯度消失、爆炸等问题所专门设计出来的一种时间循环神经网络结构。LSTM 的核心思想就是在一般RNN 单元结构设的基础上增加3 种类型的“门”，通过门限机制来控制传输状态，保留长期记忆和忘掉无用记忆，以保留最重要信息。这3 种门分别为：遗忘门、输入门和输出门，示意图如图1 所示。

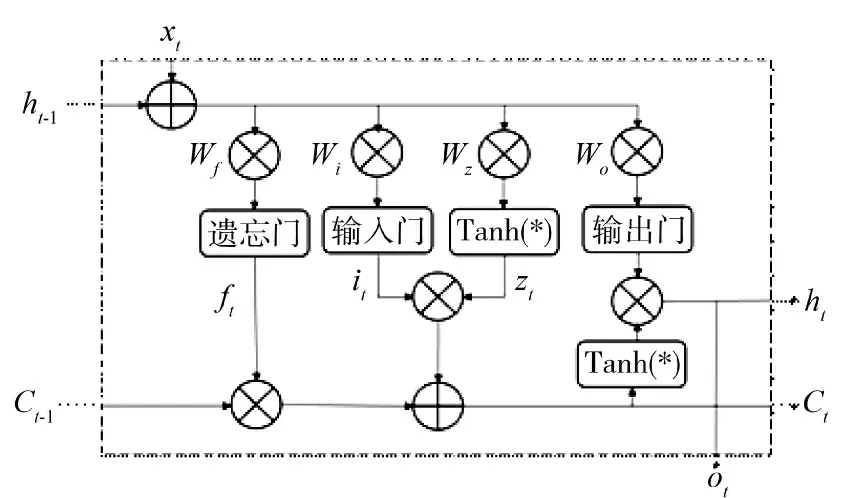
图1 LSTM 示意图

LSTM 网络模型搭构完毕后，可以运用时间反向传播（BPTT）算法来对LSTM 网络进行训练，来得到LSTM 的相关参数。

1.2 贝叶斯优化算法

贝叶斯优化算法使用概率模型代理拟合原始代价的目标函数，根据后验概率分布构造采集函数，选择下一个最优评估点。文中概率模型选择运用高斯过程回归，采集函数选择运用提升概率函数。

贝叶斯优化过程如图2 所示。

图2 贝叶斯优化过程图

1.2.1 高斯过程回归

高斯过程是贝叶斯优化的运用中应用最为普遍的概率模型。作为多元高斯概率分布的一般范化，高斯过程主要是由均值函数与半正定的协方差函数组成，即：

其中，f（x）为目标函数值，φ（*）为分布函数，μ（x）、σ（x）分别为高斯过程回归概率模型的均值和方差，α 为超参数，以探索最大值空间。α=0 使得值收敛于f（x），避免出现局部最优。

利用贝叶斯优化LSTM 进行预测的一般步骤为：

1）设定待优化参数范围，优化目标为RMSE；

2）利用贝叶斯对LSTM 的隐藏层和初始学习率进行优化；

3）返回优化的RMSE 最小值及对应LSTM 模型的超参数；

4）将贝叶斯优化LSTM 模型的超参数作为最终LSTM 模型的参数。

2 基于贝叶斯优化LSTM 的剩余寿命预测方法

基于贝叶斯优化LSTM 网络构建发动机剩余寿命预测模型，该模型在LSTM 网络的基础上，使用贝叶斯优化算法对LSTM 网络的超参数进行优化，提高预测的准确度。主要对初始学习率和隐藏层数两个超参数进行贝叶斯优化，优化超参数的约束条件如表1 所示。

表1 超参数约束条件

运用贝叶斯优化LSTM 网络超参数，进而应用LSTM 网络对航空发动机进行剩余寿命预测，其具体实现流程如图3 所示。

图3 具体实现流程图

3 实例分析

3.1 数据集介绍

验证实验数据集来自于NASA 的涡扇发动机退化数据集（C-MAPSS），该数据集记录了每台发动机在采样时间产生的数据样本，记录了从健康到故障的性能退化过程。数据集包含1 个时间数据，3 个操作模式和21 个传感器数据。具体传感器名称如表2 所示。数据集包括训练集、测试集和测试集标签。以该数据集为例，测算贝叶斯优化LSTM 算法的性能，并与其他算法进行对比分析。

表2 传感器信息表

3.2 数据预处理

3.2.1 删除常量参数

虽然训练集与测试集一共记录涡扇发动机的21种传感器数据，但其中有一部分传感器是常数量，不随样本或时间变化。换言之，这些常量参数对于航空发动机剩余寿命预测不起作用，对于模型训练也没有帮助。同时，参考其他研究中的做法，方便进行对比分析，对常量参数进行了删除操作，只选取变量传感器数据作为输入来对模型进行训练和验证。

3.2.2 数据标准化

然后，对传感器数据进行了数据标准化，方便不同量纲的数据进行分析。数据标准化的一般处理方法主要有Min-max 和Z-score 两种方法。主要采取Z-score 方法对传感器数据进行数据归一化。Z-score 表达式如下：

3.2.3 设置训练集标签

下面先各按各个样本的大小顺序进行排列。如图4 所示，可以发现大部分样本在125 以上。因为在系统前期，发动机状态比较稳定，退化较慢。为更快训练算法，按照一般做法对系统前期的数据进行裁剪，选取选取快要发生故障的样本数据，以125 对样本进行裁剪。

图4 样本数据排序图

3.3 设置网络结构

构建基于贝叶斯优化的LSTM 网络，LSTM 网络包含1 个LSTM 层、1 个池化层和两个全连接层。其中，LSTM 网络结构超参数中初始学习率和隐藏层数由贝叶斯优化迭代选优，其他参数如表3 所示。贝叶斯优化针对初始学习率和隐藏层数进行迭代寻优，迭代次数设置为10。

表3 LSTM 网络参数表

3.4 评价指标

模型评价的常用性能评价指标主要有均方根误差（root mean squared error，RMSE）和评分函数（Score）两种方法。主要采用均方根误差（RMSE）来对航空发动机剩余寿命预测模型的性能进行评价。RMSE 的表达式如下所示：

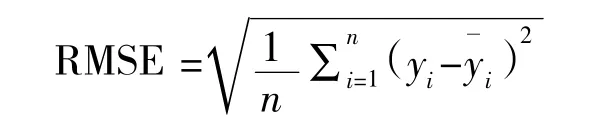
3.5 实验结果

首先利用贝叶斯优化算法对LSTM 算法的超参数进行了优化，经过迭代择优，找到了LSTM 超参数最优解，当初始学习率为0.010 177，隐藏层数为756 时，RMSE 最小，为15.188。具体贝叶斯优化过程如图5 所示。

图5 贝叶斯优化过程图

然后随机选取6 个发动机，对其剩余寿命预测情况进行观察，如下页图6 所示，贝叶斯优化LSTM算法对于航空发动机剩余寿命预测效果较好。

图6 发动机剩余寿命预测情况

3.6 对比分析

为了进一步说明预测方法的可行性和有效性，选取其他6 种预测方法，与同样数据集的研究结果进行对比分析，以充分评估贝叶斯优化LSTM 算法的效果。6 种方法同样使用RMSE 作为评价指标，具体对比结果如下页表4 所示。

由表4 可见，与MLP 和SVM 等机器学习算法相比，贝叶斯优化LSTM 结果更好，CNN 等常规深度学习模型也取得了更好的结果。和Bi-LSTM 、BHSLSTM 和LSTM 等优化算法相比，RMSE 评价结果分别提升了9.595%、19.128%和5.898%。这是因为利用贝叶斯优化算法对超参数进行了迭代择优，克服了手工调整的弊端，能更好地利用深度学习网络进行预测。因此，在航空发动机剩余寿命预测上取得更好的结果。

表4 RMSE 对比分析表

4 结论

航空发动机作为最重要的航空器部件，实时监控健康状态、准确预测剩余寿命，能有效提高航空器的可靠性和安全性，并为制定维修策略提供参考依据。根据深度学习和优化算法，提出了贝叶斯优化LSTM 算法的航空发动机剩余寿命预测方法。方法利用贝叶斯优化算法优化LSTM 网络的隐藏层数和初始学习率，将使用该组超参数在验证集上的RSME 作为目标函数；基于目标函数过去的评估结果建立替代函数找到最小化目标函数的值，并作为超参数；利用贝叶斯优化的LSTM 函数对发动机剩余寿命进行预测，然后通过NASA 公开数据集对该方法进行了验证。通过与其他6 种算法的比较可以得出，贝叶斯优化LSTM 算法能更好地进行参数优化，具有更高的预测精度，在航空发动机进行剩余寿命预测方面应用效果较好。