空中目标威胁的ABC-RVM 评估方法

牛军锋，甘旭升，刘 影，韦 刚，刘 飞

（1.西京学院管理技术系，西安 710123；2.空军工程大学空管领航学院，西安 710051；3.空军工程大学防空反导学院，西安 710051）

0 引言

随着空中进攻武器的不断发展，水面舰艇，尤其是类似航空母舰、两栖攻击舰等这样的大中型舰艇，面临的空中威胁越来越严峻，特别是面对多平台联合突防、多批次协同饱和攻击时，水面舰艇承受的空中压力会更大。因此，在既有防空信息基础上，借助科学手段，实时准确地对空中来袭目标的攻击意图、威胁程度进行评估判断，是提高水面舰艇生存率的关键。

在防空作战中，由于空中态势的复杂性和多变性，通常无法确切描述各影响因素与空中目标威胁之间的解析关系，这给空中目标威胁评估工作造成了非常大的困难。为此，学者经过不断地研究和探索，总结并提出了诸多目标威胁评估方法，其中比较典型的，诸如贝叶斯网络、直觉模糊集、神经网络和支持向量机（support vector machine，SVM）等。然而，这些方法在参数设置、计算复杂性、实现难度、满足精度要求等方面都或多或少存在着不足。本文则主要围绕相关向量机（relevance vector machine，RVM）在舰艇空中目标威胁评估中应用展开研究。与SVM 相比，RVM 的核函数不需要符合Mercer 条件，并极大地减少了计算量。然而，在工程实践中，由于核函数选取与参数优化等问题的限制，仅仅通过单一RVM，往往难以达到理想效果，需要探索借助其他方法解决RVM 应用中存在的问题。

基于此，在构建RVM 模型过程中，构造了混合核函数，并引入人工蜂群（artificial bee colony，ABC）算法［8］优化所涉及的参数，以实现对空中目标威胁的准确科学评估并给出了验证。

1 确定空中目标威胁指标

通过对大量文献资料的阅读和准备，结合海上空中防御作战的特点，广泛征求有关专家、舰艇作战人员与指挥人员的意见和建议，为评估空中目标威胁设计了包含18 个影响因素条目的问卷调查量表，并采用相关统计分析工具判断它们的一致性（即设计的影响因素能否反映空中目标威胁的真实情况）。影响空中目标威胁的因素及其相关系数与Alpha 系数如表1 所示。

表中Alpha 系数与相关系数用于检验一致性。

1.1 Alpha 系数

Alpha 系数本文指克伦巴赫Alpha 系数，它是信度（问卷的可信程度）的量度，用于测验一致性、稳定性和可靠性，其计算公式

根据统计标准，Alpha 系数值大于0.7，可认为条目之间的内在一致性较好，通过计算，表中18 个条目的Alpha 系数值为0.791，说明这18 个条目的内在一致性较高。而表中的Alpha 系数值是指：每当去掉一个条目后余下条目的Alpha 系数值。如删除“目标进攻样式”条目后，余下17 个条目的Alpha 系数值为0.814，也就是剔除该条目后，Alpha 系数值从原来的0.791 增加至0.814。而表1 中的18 个条目的Alpha 系数值都大于0.7，说明所设计的18 个因素能够反映目标威胁的实际。

表1 影响因素及其相关系数与Alpha 系数

1.2 相关系数

相关系数用以刻画两个变量线性相关程度的统计量。常用的Pearson 相关系数公式可表示为

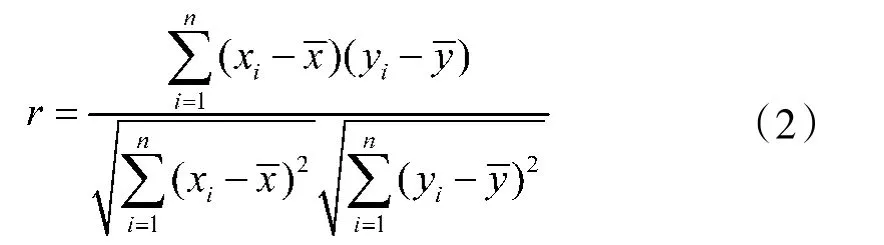
相关系数值主要用于判断所要去掉的冗余条目，通常来说，如果r＜0.4（可视情况而定），就可认为该条目与其他条目的相关性不强，可以去除。据此可删除初始问卷中r＜0.4 的影响因素，并对处理后的因素作新一轮问卷和统计分析，最终得到去除后的因素及其相关系数与Alpha 系数，如表2 和表3 所示。

表2 去除后的因素及其相关系数与Alpha 系数

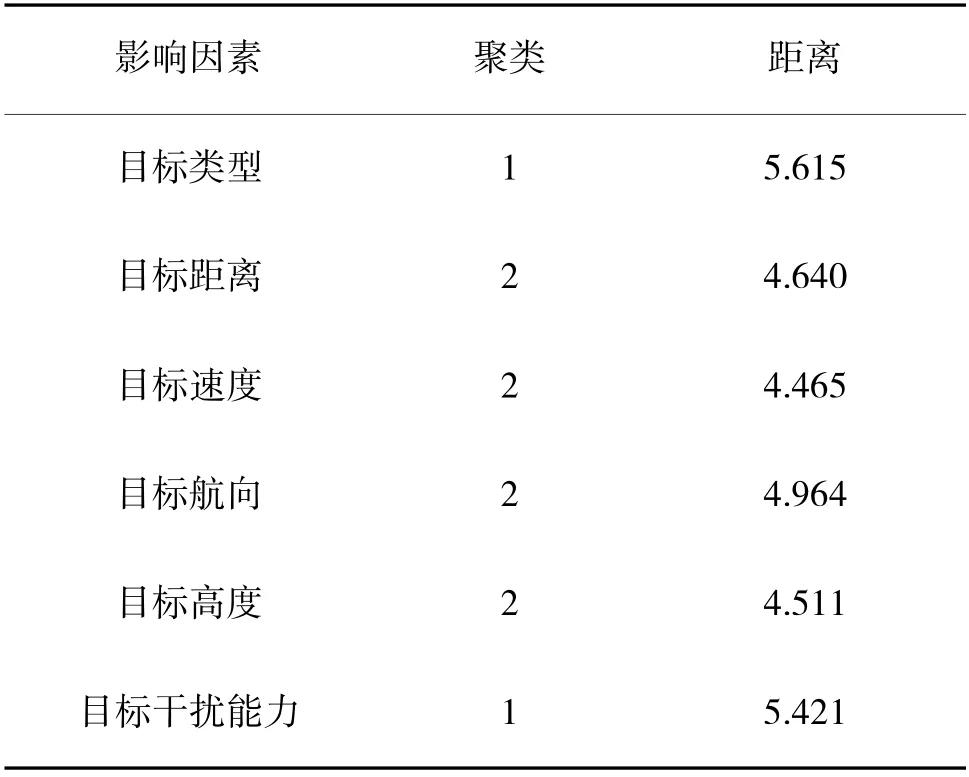
表3 去除后的因素聚类结果

去除表1 中相关系数较小因素后，表2 中共有6 个影响因素，它们Alpha 系数值都大于0.8，没有发现过低的系数，基于此，可建构如图1 所示的空中目标威胁指标体系。需要说明的是，通过前述过程选定6 个因素作为目标威胁指标，并不意味着与表1 中其余因素没有关系，而是这6 个因素更具代表性。例如：目标航路捷径就是空中目标威胁的一个重要参数，它是指防空火力发射点至空中目标的航向在水平面上投影的垂直距离。可以看出，该参数与目标航向和目标距离密切相关，因此，既然指标体系中包含目标航向和目标距离，就无需选取目标航路捷径作为威胁指标。

图1 空中目标威胁指标体系

2 基于ABC 算法的RVM

2.1 人工蜂群算法

ABC 算法是模仿蜜蜂的采蜜过程而发展起来的一种的新型群体优化算法。它通过蜂群中侦察蜂跟随蜂和引领蜂之间的互相配合、协调合作，完成对最优解或次优解的搜索。从生物学特性，引领蜂在寻优空间搜索到蜜源后遂行采蜜，并把该蜜源信息传送给跟随蜂，所以，算法设计时，引领蜂需占整个蜂群的一半，余下都为跟随蜂，侦察蜂主要通过角色转变来解决。在算法寻优过程中，引领蜂主要用于搜索蜜源周边的邻域，同时给出候选蜜源区，跟随蜂的角色是根据贪婪机制找到相对优质蜜源进行采蜜；侦察蜂的角色是寻找新蜜源进行采蜜。

在给定的解空间内，每个蜜源都可视为一个可行解，不难理解，在待优化问题中，适应度值对应于各蜜源的蜜汁丰富程度；求解速度对应于搜索蜜源的速度；全局优化解对应于蜜汁最丰富的蜜源。

1）初始化种群，可根据式

4）跟随蜂按照轮盘赌策略选择蜜源。选择蜜源后，跟随蜂就转化为引领蜂，重新回到式（4）搜索蜜源

式中，P是蜜源x被选择的概率。如果某蜜源大于预定阈值未更新，说明已放弃该蜜源，则跟随蜂变成侦查蜂，根据式（3）作新的全局搜索。

2.2 相关向量机回归

RVM 通过贝叶斯推断获得权重概率分布中参数的优化值，它能在概率意义下进行合理划分，使得预测函数针对训练集似然函数值最大。

2.3 基于ABC 算法的多核RVM 参数优化

对于RVM，其核函数的选取及其构成方式对预测精度有很大的关联性。通常情况下，单一核函数是RVM 应用中的标准设计，这可能会使模型达不到理想的预测精度，且限制了建模的灵活性。Gauss核函数映射出的特征空间中，所有数据都被约束在一个无形的球里，体现了局部核函数的特性。而Sigmoid 作为核函数，往往体现出良好的全局性质。基于此，将两者有机结合，构造一种混合核函数，不仅能集中两种核函数的特点，还可兼具局部和全局特性，进而改善模型的预测性能。

本文在构造混合核函数时，主要通过以下方式

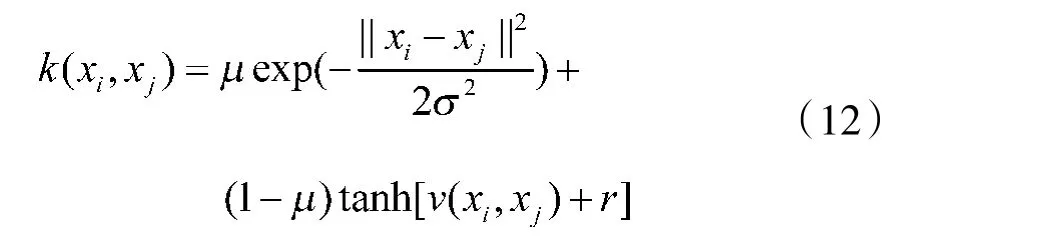
其中，μ 为调节系数，且0 ＜μ＜1，r 为常值。不难看出，RVM 建模过程需要优化确定的参数为μ，σ，r。也就是说，要提高RVM 模型的预测精度，必须通过某种算法对参数μ，σ，r 执行最优化过程，找出最优解或次优解。本文主要采用ABC 算法优化多核RVM 的参数组合μ，σ，r，其具体实现步骤如下。

3 基于ABC-RVM 的空中目标威胁评估

3.1 空中目标威胁指标量化

1）目标类型：依据威胁程度，将直升机、小型目标（如隐身飞机、巡航导弹）、大型目标（如歼击轰炸机）的威胁值依次量化为8，5，3。

2）目标干扰能力：按照无、弱、中、强4 个等级，将目标干扰能力依次量化为8，6，4，2。

3）目标距离：在0 km～450 km 区间内，每50 km为一个等级，将目标距离量化为9～1。

4）目标速度：在0 m/s～1 800 m/s 区间内，200 m/s为一个等级，将目标速度量化为9～1。

5）目标航向：在0°～36°区间内，每4 °为一个等级，将目标航向量化为9～1。

6）目标高度：按照高、中、低、超低4 个等级，将目标高度依次量化为8，6，4，2。

3.2 空中目标威胁度计算

3.3 ABC-RVM 空中目标威胁评估模型

要进行空中目标威胁评估，其基本思路：采用ABC 算法优化RVM 的参数；将获取的最优参数μ，σ，r 用于构建RVM 评估模型；通过该模型进行威胁评估。为适应该建模过程，原始样本数据需要预先进行必要的量化和标准化处理。图2 给出了空中目标威胁ABC-RVM 建模评估流程，其中，Num 为终止迭代次数，Lim 为蜜源的最大搜索次数。从图中可看出，建模过程着重需解决以下几个问题：1）样本数据构造。将评估指标的目标类型、干扰能力、距离、速度、航向和高度作为输入变量；将空中目标威胁计算值作为输出变量。为确保模型性能，随机选取一部分样本数据作为训练集，余下用于模型测试。2）样本数据预处理。主要包括数据量化和归一化。将定性指标数据量化，并减少量纲差异带来的不利影响。3）ABC 算法优化参数。通过ABC 算法的优化过程获取多核RVM 的最优参数μ，σ，r。4）训练RVM 模型。在优化参数μ，σ，r 基础上构造RVM，即可输入训练集数据，选取适当算法训练RVM，直到满足精度需求，训练停止。5）空中目标威胁测试。训练完成后，便可利用测试样本进行模型验证。

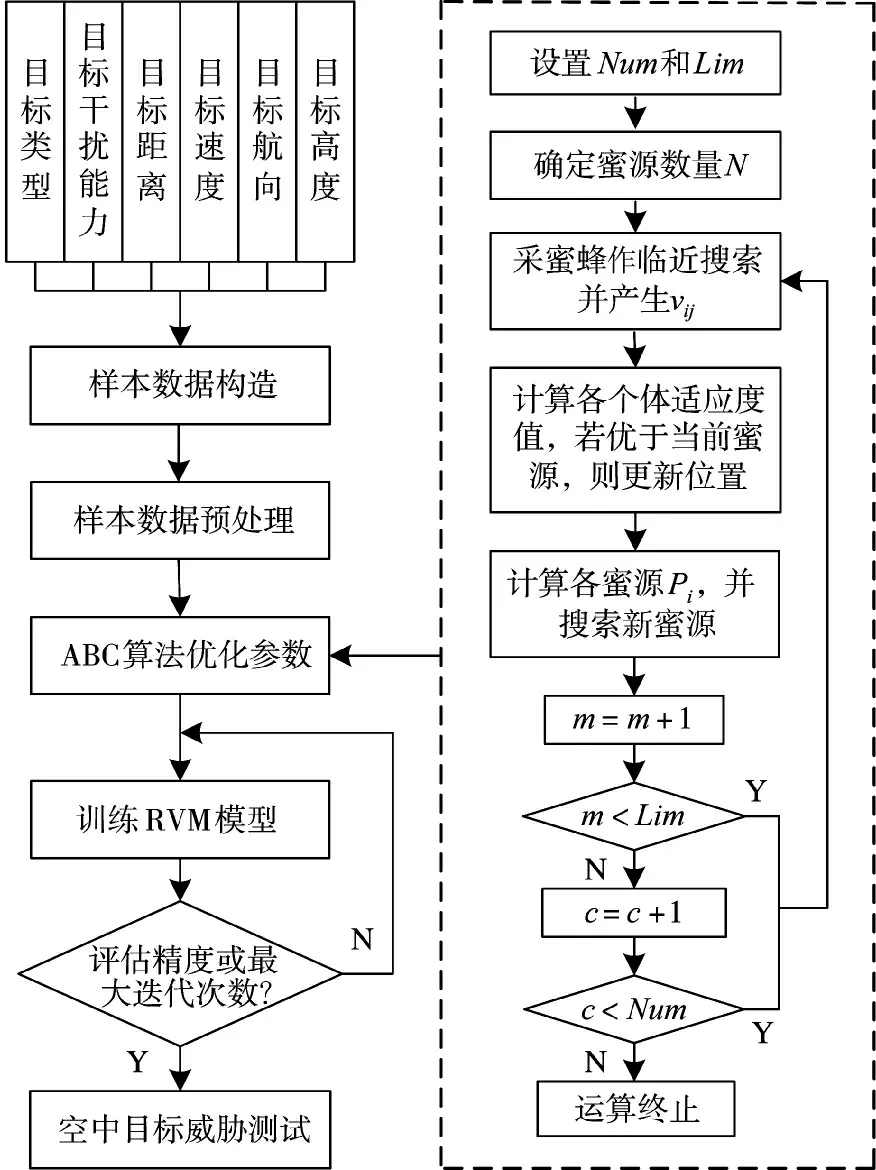
图2 空中目标威胁ABC-RVM 建模评估流程

4 仿真验证

4.1 样本数据预处理

根据前述的威胁指标和建模流程，即可对空中目标威胁进行建模和评估。实验数据来源于文献［4］。训练集选取60 组数据，包含直升机、小型目标和大型目标各20 组，15 组用于测试，直升机、小型目标和大型目标各5 组。部分原始及其量化后的样本数据如表4 和表5 所示。此外，在建模前，还需将表2 中的样本数据进行归一化，即将威胁指标变换为无量纲形式。

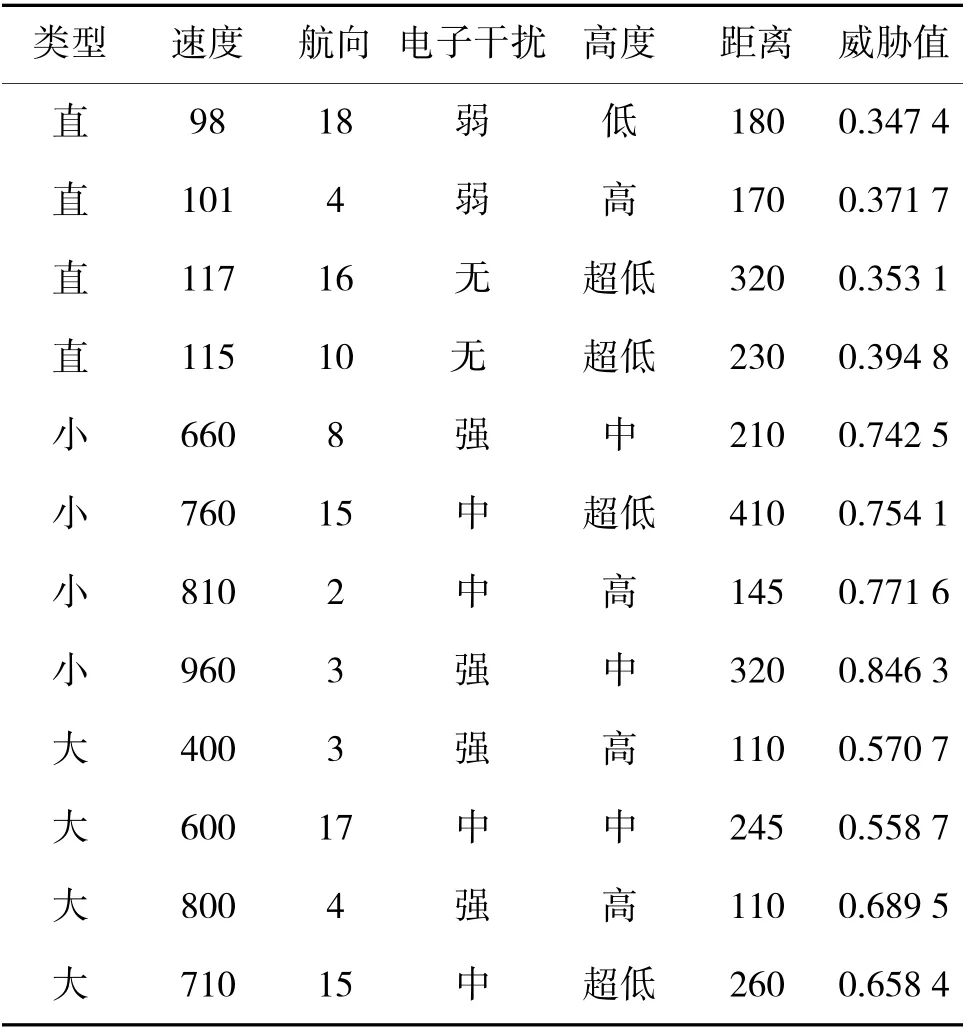
表4 部分原始样本数据

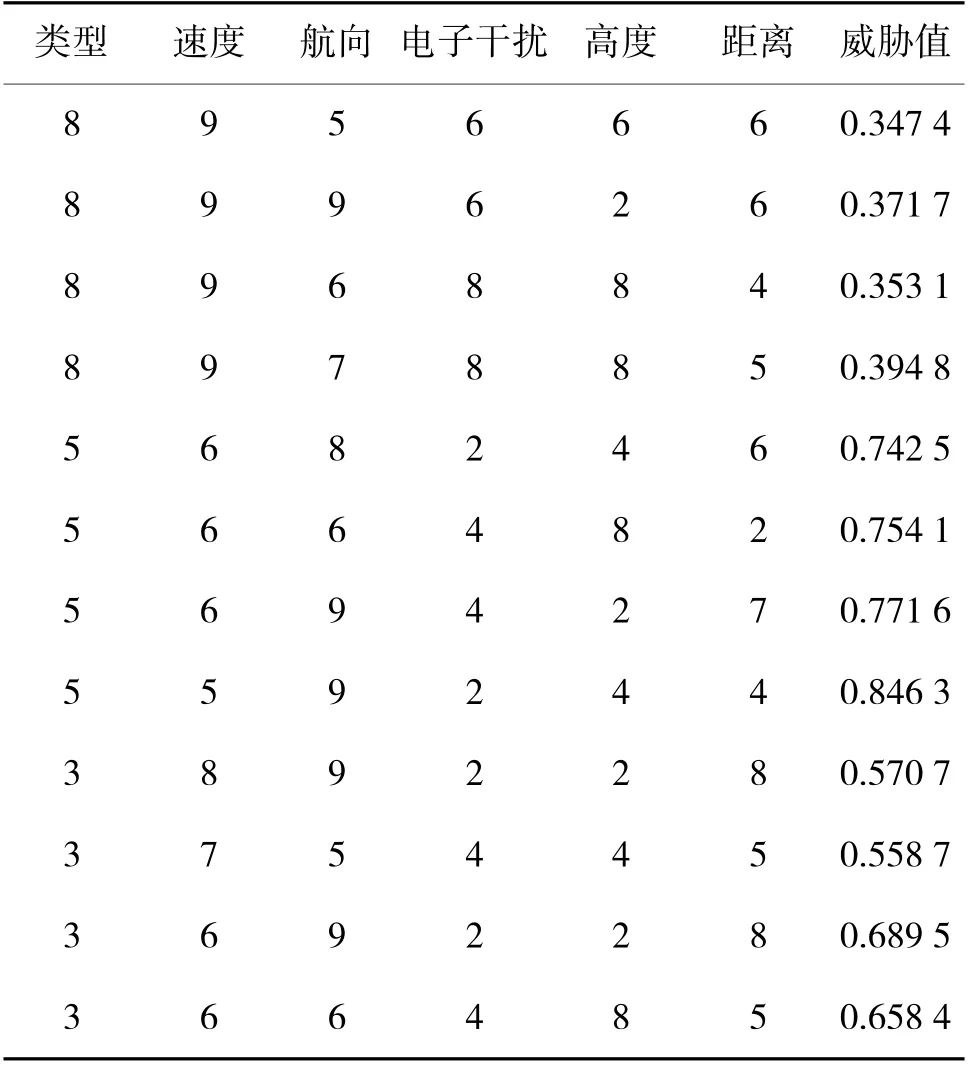
表5 部分量化后的样本数据

4.2 仿真结果分析

对样本数据预处理后，即可根据图2 流程构建空中目标威胁ABC-RVM 模型。在采用ABC 算法优化RVM 核函数参数组合［μ，σ，r］时，适应度函数设为训练数据预测的均方根误差。ABC 算法优化过程中最优个体适应度值变化如图3 所示。可以看出，ABC 算法在蜂群规模为30 情况下，经过69 次迭代计算即收敛于最优适应度值0.006 2，算法达到收敛，获得最优参数［μ，σ，r］=［0.632，1.585，4.241］。这说明ABC 算法仅需要较小代价，就能搜索到最优的参数组合。

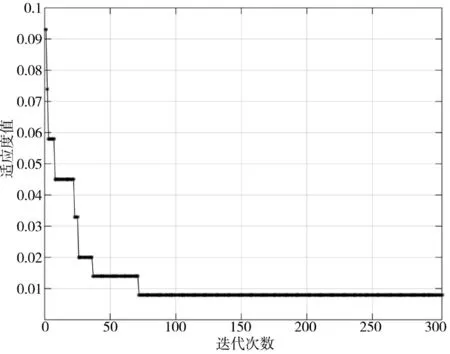
图3 ABC 算法进化过程

为验证ABC-RVM 应用中的优势，可基于相同仿真背景，分别计算Gauss 核的RVM（Gauss-RVM）和Sigmoid 核RVM（Sigmoid-RVM）的评估结果并作对比分析，模型评价指标采用平均绝对误差（MAE）、平均相对误差 （MRE）和均方根误差（RMSE）。测试样本实际值与评估值如表6 所示。图4 给出了评估误差的绝对值对比。

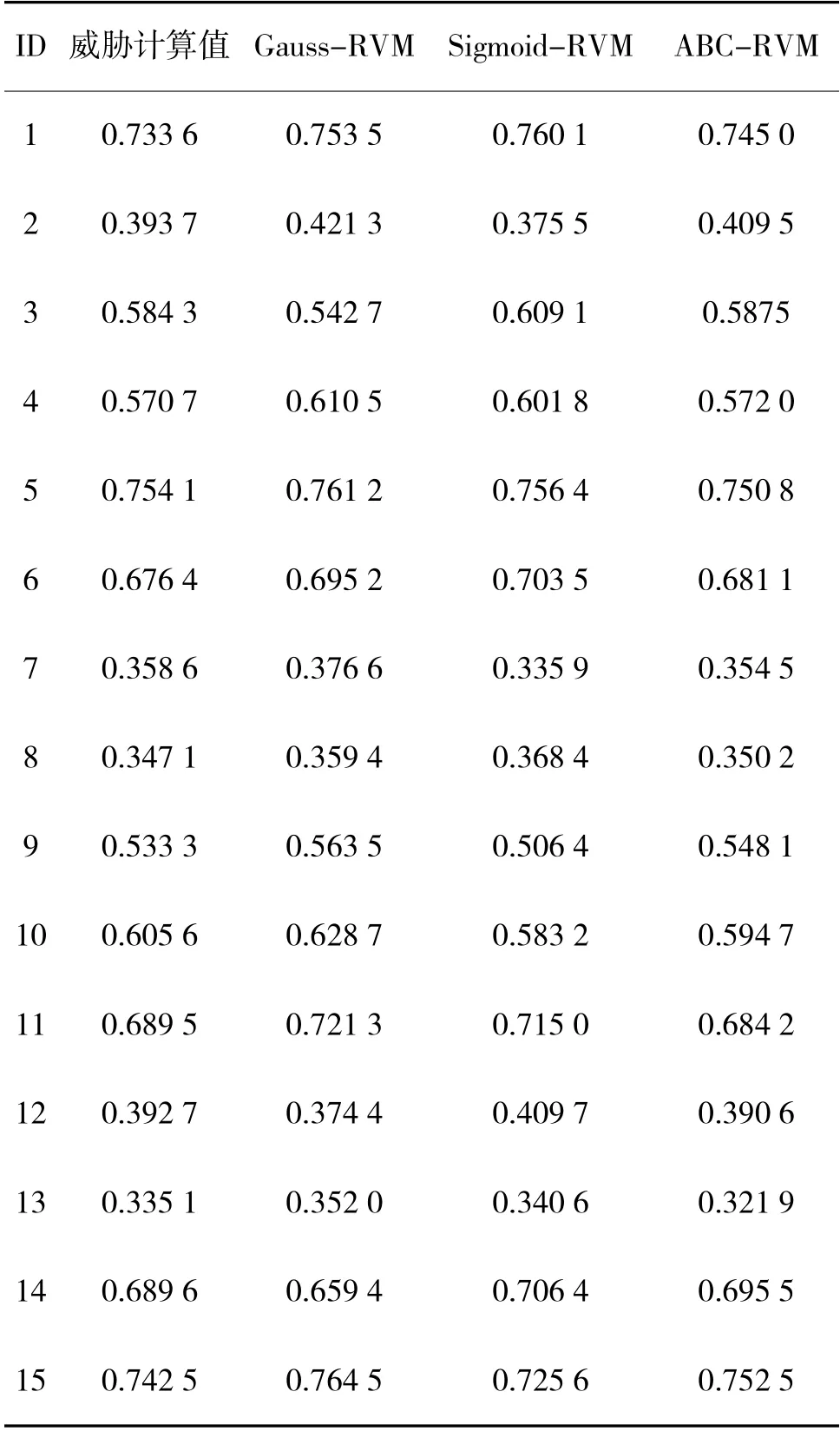
表6 测试样本的计算值与评估值

由表2 和图4 可知，对于ABC-RVM，除第5 和12 号样本的评估精度略低于Sigmoid-RVM 外，其他样本均优于Gauss-RVM 与Sigmoid-RVM，并且ABC-RVM 评估的误差绝对值总体都低于0.015。加之表7 在各项评价指标上的对比，不难得出：Gauss-RVM 与Sigmoid-RVM 对空中目标威胁评估都存在明显偏差，即基于单一核的RVM 在处理复杂非线性问题时仍显不足。而ABC-RVM 通过利用Gauss核与Sigmoid 核的各自优点并进行合理加权组合，对处理类似于空中目标威胁评估的复杂非线性问题时，能够取得较为满意的评估效果。

表7 3 种方法评估精度对比

图4 评估误差绝对值对比

5 结论

将Sigmoid 核函数的全局优化特性与Gauss 核函数的局部优化特性加权结合，采用ABC 算法优化多核参数，建立基于ABC 算法优化多核RVM 空中目标威胁评估模型。通过仿真结果比较分析，证实该方法在处理类似于空中目标威胁评估的复杂非线性问题具有较大优势，该方法评估结果的各项精度指标值均优于单一核的Gauss-RVM 与Sigmoid-RVM 的评估结果，证实该方法具有较高的评估精度。本文方法采用ABC 算法获取RVM 最优参数，无需人工设置参数。与SVM 相比，RVM 不仅在理论上可极大减少核函数的计算量，而且RVM 使用专有的MATLAB 工具箱，更便于算法实现。