异构无人平台不规则区域协同侦察部署方法*

刘子宸，曲俊海，马跃东

（北方自动控制技术研究所，太原 030006）

0 引言

在未来高动态、强对抗和不确定任务的无人化陆战场，以异构无人作战平台结合有人装备的有人/无人混合编队，将成为执行区域作战任务的主要力量。有人/无人混合编队处于作战的最前沿地带，对接敌区域的侦察和封控尤为重要。如何将编队中各异构有人/无人平台携带的可见光、红外、雷达等多型侦察装备进行最优化的协同侦察部署，使得各平台在最短时间内，经过最短的移动距离，同时规避陷阱和悬崖等不可到达区域，实现复杂目标区域的全域侦察监视或多频谱覆盖，从而有效提升目标发现概率，发挥侦察装备的最大效能，成为一个亟待解决的问题。

针对多传感器的区域部署任务规划问题，当前的技术途径主要包括基于数学规划的多约束问题、专家系统、基于智能算法的启发式搜索等方法。近年来，启发式搜索算法发展迅速，原理简单且在收敛速度上优势明显，其中，对PSO 算法的改进研究最为广泛。文献［9］提出一种改进的PSOSA算法，对初始随机分布的移动传感器进行重新部署，以获得最优的覆盖效果。文献［10］引入模拟退火方法改进粒子群算法，通过限制原始粒子和新粒子在迭代过程中的位置变化，可有效改善算法的收敛速度。文献［11］在标准粒子群算法的基础上引入模糊数学的思想，能够在传感器部分加入和全部加入两种情况下均取得较好的覆盖效果。文献［12］提出一种基于多目标局部变异- 自适应量子粒子群优化（LM-AQPSO）算法，对复杂地形环境下的多传感器部署问题进行研究，构建了多传感器多目标优化部署模型。

当前的研究主要针对同种类型的多个传感器，部署区域为规则的正方形区域，未考虑异构传感器在任意不规则的凸/凹多边形区域的最优化部署问题，因此，在实际应用中受到了一定限制。

针对未来无人化陆战场有人/无人混合编队中异构平台携带的多型侦察装备的协同侦察部署问题，本文提出了自适应粒子群- 区域最优匹配（PSO-ROM）算法。采用参数自适应和局部变异方法对粒子群优化算法进行改进，对异构平台中探测性能最优的多个同类型传感器进行优化部署；依次针对异构平台中的多个其他类型传感器，采用区域最优匹配算法对尚未覆盖的空白区域进行优化部署，直至达到侦察部署目标。基于PSO-ROM 算法不仅可用于异构无人平台不规则区域协同侦察部署问题，还可实现重点区域的多频谱覆盖，提升侦察探测效能。

1 问题描述

1.1 地形模型

在实际作战任务中，待侦察区域多为不规则的多边形起伏区域。与理想的平坦区域相比，起伏区域表面由于存在电磁波的反射和吸收等现象，平台所携带传感器的侦察探测范围将受到不同程度的影响。根据表1 所示的地形起伏度标准，结合平台传感器在开展侦察时升高幅度等因素，本文研究的侦察部署算法适用场景为：海拔高度低于400 m，局部地势（16 km内高差）低于75 m 的低平起伏与和缓起伏的平原、丘陵和高原等地形。

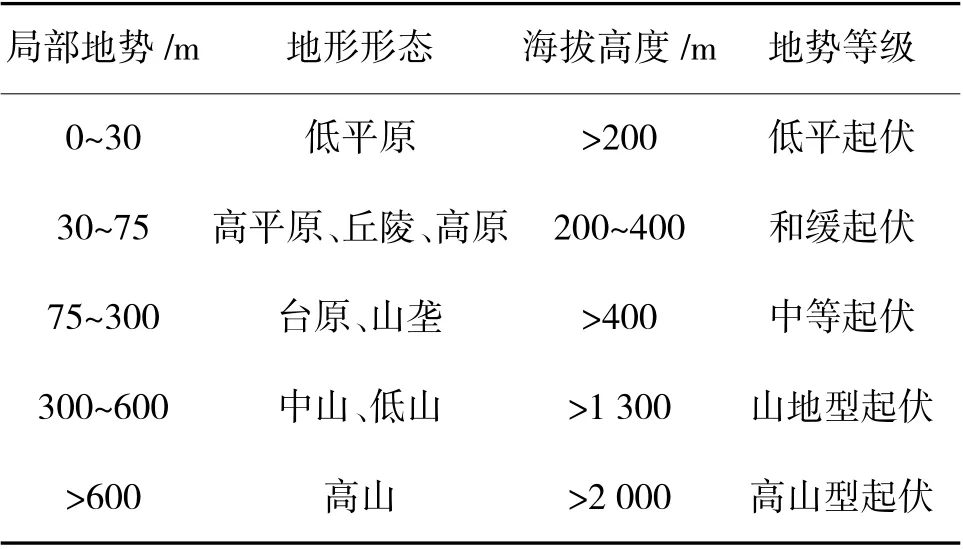
表1 地形起伏度标准

为简化地形模型，将协同侦察目标区域建模为任意多边形区域，可分为凸多边形和凹多边形区域两种情况，典型的凹/凸多边形任务区域示例如下页图1 所示。有人/无人混合编队集结区域（图中绿色圆形区域）的圆心位于坐标原点，多边形区域内的“*”代表陷阱、障碍等不可到达/部署位置。

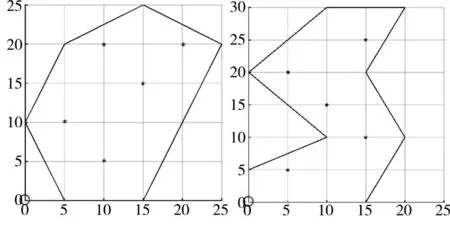
图1 边界复杂的典型多边形搜索任务区域示例

1.2 传感器探测模型

针对不同的探测需求，有人/无人混合编队各平台携带了多种传感器，主要分为可见光、红外、雷达等类型。各传感器的探测半径会因气候条件和能见度的差异而有所不同。假定在理想的能见度条件下，异构传感器的探测能力如表2 所示。

表2 传感器参数模型

为了简化，本文中的传感器覆盖感知模型采用二元感知模型，即以传感器位置p 为圆心，探测半径为r 的圆。r 的大小根据传感器的性能而定，在圆内所有位置的探测概率是一致的，传感器在p 点对目标点q 的探测概率g（p，q）可表示为：

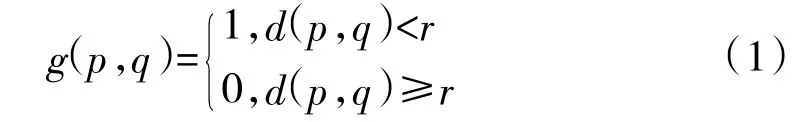
其中，d（p，q）为p 点和q 点之间的直线距离。

1.3 目标函数

异构多传感器的协同侦察部署属于典型的多目标优化问题，包含以下优化目标：1）搜索覆盖率R：即多传感器部署完成后，对任务区域的覆盖率，覆盖率越高越好。在重点区域多频谱覆盖中，多频谱传感器的覆盖率同样越高越好。2）传感器数量N：由于传感器数量有限，因此，在达到区域侦察覆盖目标的前提下，使用的传感器数量越少越好。3）平均移动距离L：由于无人车存在续航问题，车辆从集结地到达部署目标位置的平均移动距离越短越好。本文不考虑基于路网信息的有人车/无人车路径规划问题，因此，平均移动距离L 取集结地到最终部署位置的直线距离。

综上所述，目标函数为：

式中，α 和β 为权重因子，可根据实际作战任务需求及各有人/无人平台油/电剩余量及续航状态进行设置。

2 自适应粒子群- 区域最优匹配（PSO-ROM）算法

本文用覆盖比F 来表征待部署传感器资源相

采用PSO-ROM 算法的异构多传感器部署流程如图2 所示，R为任务要求达到的最低覆盖率；Z为待部署传感器的类型数量；k 为当前正在部署的传感器类型（k=1，2，…，Z）。在读取任务信息、地图信息和传感器资源信息后，首先判断覆盖比F 是否高于任务要求达到的最低覆盖率R，如果是，则进行下一步；否则，表明传感器资源无论在何种条件下都不足以满足任务要求，因此，跳出流程。然后，基于任务需求与无人平台资源状态设置目标函数的权重因子。对异构平台携带的探测性能最优的多个k 型传感器（k=1），使用改进的PSO 算法进行优化部署，部署完成后，判断是否实现部署目标。如果实现部署目标，则结束程序；否则，依次对异构平台中剩余的多个k 型传感器（k=2，3...，Z），采用区域最优匹配算法在尚未覆盖的空白区域内进行优化部署，直至实现部署目标或Z 型传感器已全部部署完为止。

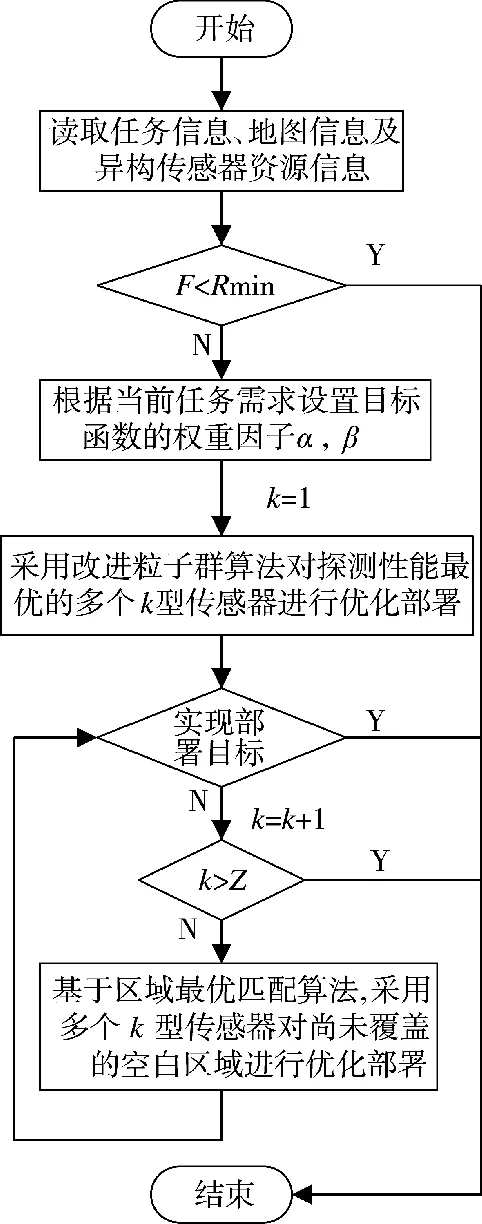
图2 采用PSO-ROM 算法的异构多传感器部署流程图

2.1 局部变异自适应粒子群算法

2.1.1 自适应粒子群算法

粒子群寻优算法的基本原理如式（4）所示：

2.1.2 规避不可到达区域的粒子群局部变异

由于存在一些不可部署区域，在算法寻优的过程中，粒子会不可避免地到达这些位置。此时，需要对进入不可部署区域的粒子进行局部变异，使粒子返回可部署区域。

假设粒子当前位置为（X，Y），运动调整后，移动至不可部署区域的位置为（X'，Y'），采用式（6）对该粒子进行局部变异调整：

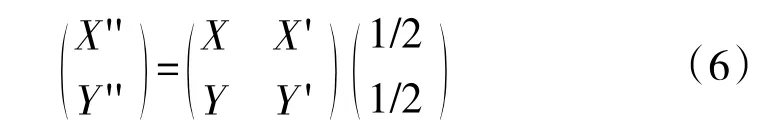
根据当前位置和目标位置的坐标连续使用式（6）进行迭代调整，直至粒子脱离不可部署区域。变异过程如图3 所示。

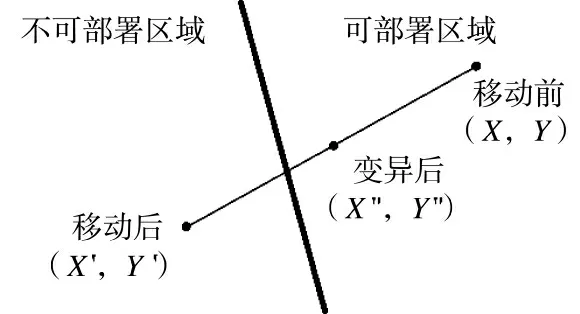
图3 局部变异过程示意图

2.2 区域最优匹配算法

对剩余的传感器资源按照探测能力进行降序排序，生成传感器队列Q。以队首传感器Q探测半径的1/4 为步长，从距离集结地最近的任务区域开始向远离集结地方向，呈射线状扫描任务区域内的未部署区域，对发现的可部署位置P与Q进行匹配，匹配阈值K 定义为：

式中，S为Q的理论最大可探测面积；S为Q部署在P后新增的任务区域覆盖面积。阈值K 的取值范围一般为（0.5，1］，可根据实际情况调整。当传感器Q满足阈值约束时，将Q出队并部署在P处；否则，继续扫描并寻找新的P'，直至部署目标实现或队列Q 为空。具体流程如图4 所示。

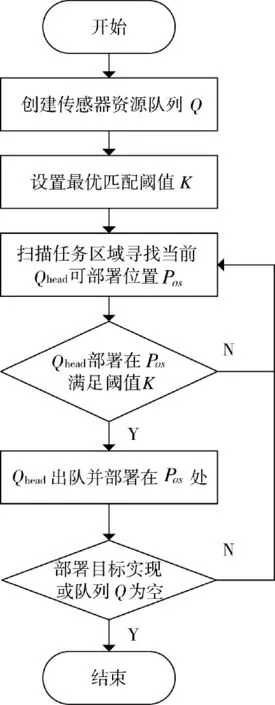
图4 区域最优匹配算法流程图

2.3 传感器与不规则多边形相对位置的判断

传感器在优化部署的过程中，每次寻优部署都需要判断传感器是否移动到任务区域外部。一般采用射线法判定传感器与不规则多边形的相对位置。在射线法中，如果射线与多边形的交点总数为奇数时，判定当前点在多边形内部；如果交点总数为0 或偶数，则判定当前点在多边形外部。由于射线法在奇异情况下容易造成误判，无法正确识别当前点是否真正在多边形区域内，本文通过对奇异情况进行分类，选取随机射线对射线法进行改进。

假设当前传感器位置为P（x，y），在多边形区域D 内随机部署。首先判断点P 是否与区域D 的顶点及各边重合。在排除点在多边形的某条边或顶点上的奇异情况后，假设区域D 的边界范围最大值为X和Y，取当前点P 远处随机点P'（x'，y'）：

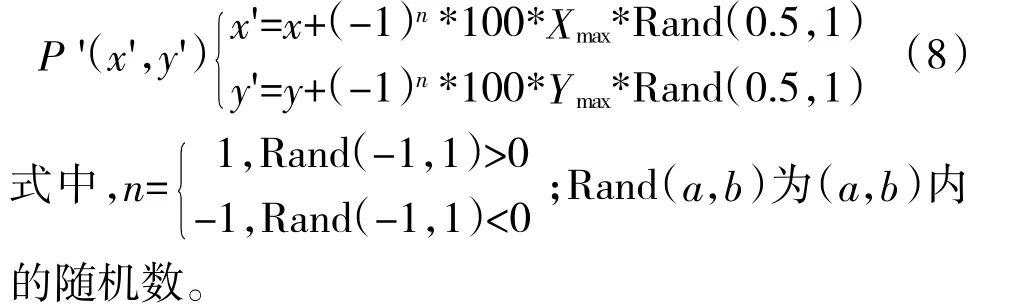
由P 点做经P'点的射线L，通过连续取多条随机射线的方式来消除L 经过多边形顶点这一奇异情况的影响。随机取所有随机射线中的两条进行判断，当两次判断结果一致时，即可确定当前点是否在多边形内部。

3 实验结果

采用Qt5.12 编译平台，C 语言编程对PSO-ROM算法的效果进行验证，并与传统粒子群算法进行对比。

3.1 异构多传感器不规则区域部署结果

如图5、图6 所示，在面积均为484 km的凸多边形任务区域1 和凹多边形任务区域2 中，采用PSO-ROM 算法和传统的PSO 算法，对传感器资源（覆盖比F=1.2）进行优化部署如表3 所示，各传感器的初始集结位置设为坐标原点。在优化部署中，区域1 和区域2 的网格数量为20×20，目标函数的权重因子α=0.5，β=10。传感器的部署效果如图5 和图6 所示，图中红色、粉色和蓝色圆分别代表A、B、C型传感器的部署位置。采用PSO-ROM 算法和传统PSO 算法的部署结果对比如表4 所示。

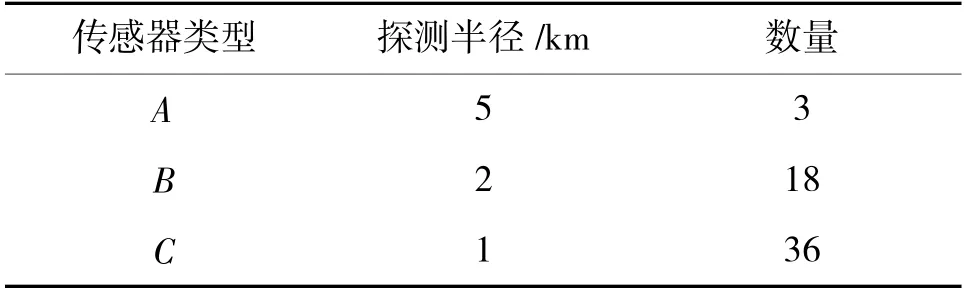
表3 待部署传感器资源列表

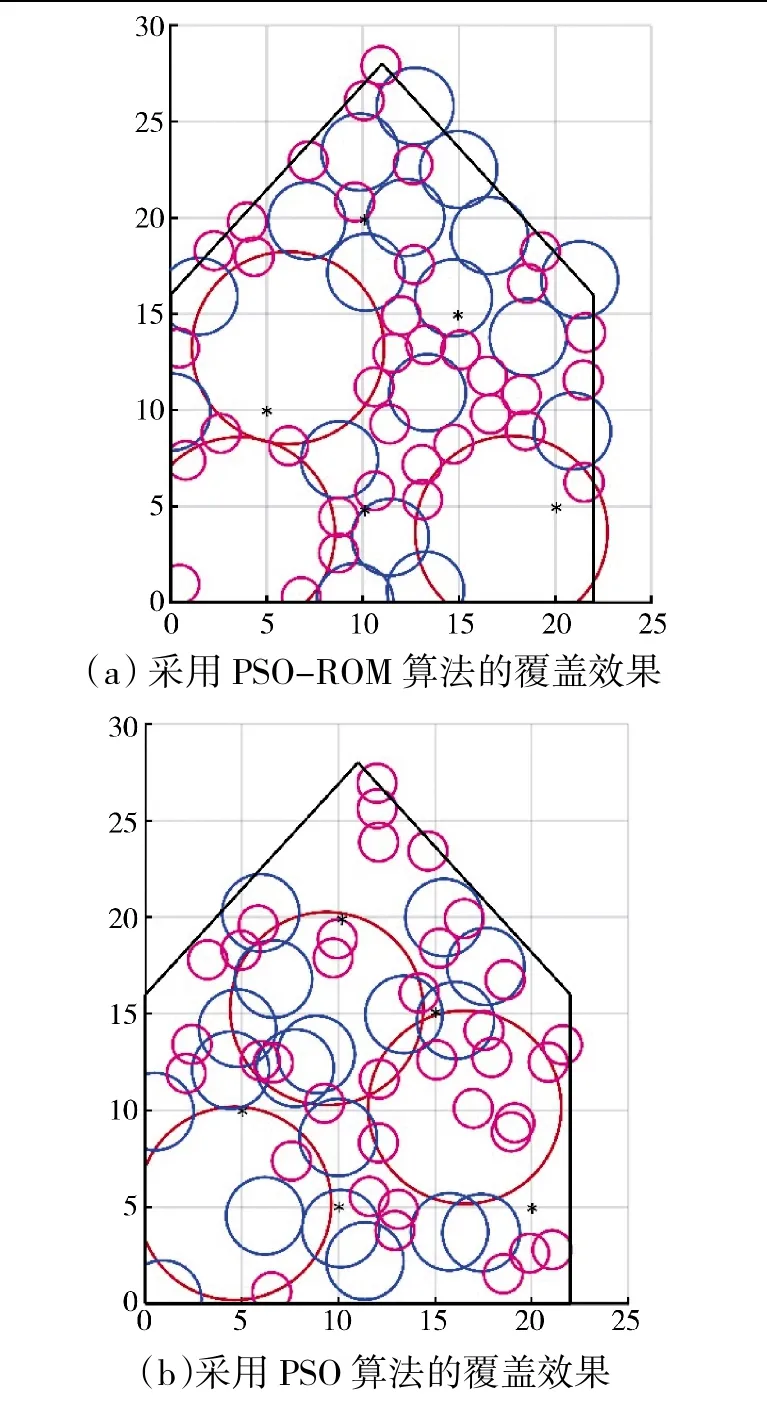
图5 采用PSO-ROM 算法和PSO 算法的凸多边形任务区域1 的覆盖效果

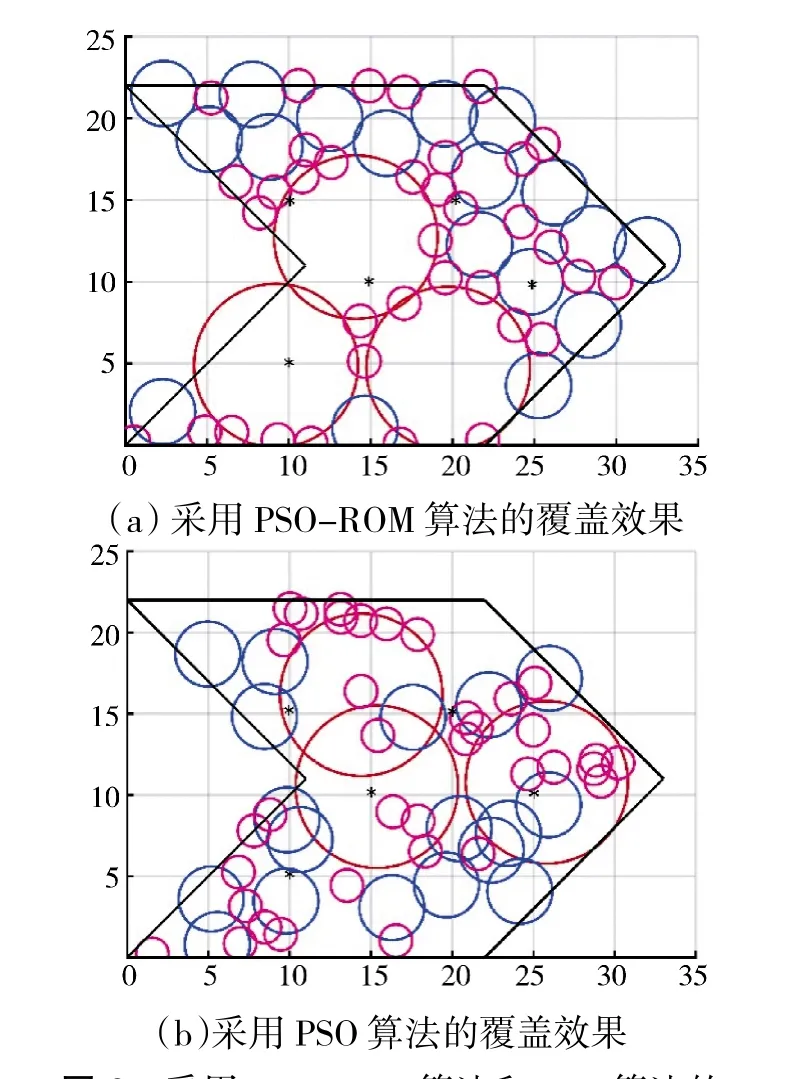
图6 采用PSO-ROM 算法和PSO 算法的凹多边形任务区域2 的覆盖效果

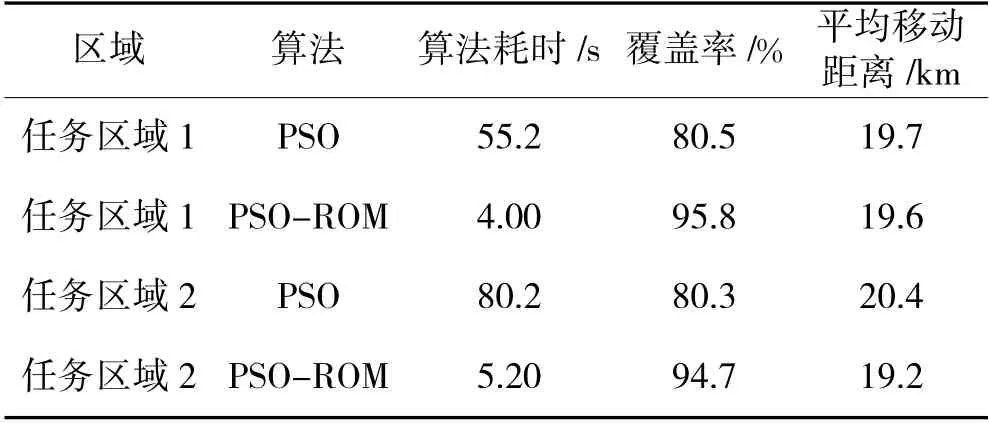
表4 PSO-ROM 算法和传统PSO 算法的部署结果对比

如表4 所示，相比于传统的PSO 算法，采用PSO-ROM 算法覆盖率平均提升14.9%，耗时平均缩短91%，移动距离平均缩短0.65 km。算法时间消耗的降低，部分原因是采用PSO-ROM 算法，将整个区域的部署问题转化为采用不同类型传感器进行多阶段部署，降低了每次寻优问题的传感器规模。如图7 所示，在任务区域之中，采用传统的PSO 算法，在耗时30 s 后取得了77.5%的覆盖率，与PSO-ROM算法耗时5.2 s 收敛得出的部署结果相比，覆盖率相差17.2%，平均移动距离相差1.2 km。在任务区域1中作相应的对比，也有相似的结果。

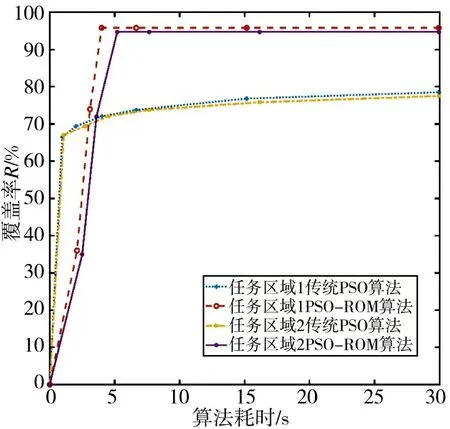
图7 传统PSO 算法与PSO-ROM 算法耗时与覆盖率的关系

3.2 重点区域多频谱覆盖

如图8、图9 所示，在面积均为550 km的凸多边形任务区域3 和凹多边形任务区域4 中，分3 次采用PSO-ROM 算法对如表5 所示的多型可见光、红外、雷达传感器资源（覆盖比F=1.2，注意设定的各传感器探测半径非真实值）进行重点区域多重覆盖部署。各传感器的初始集结位置设为坐标原点。在优化部署中，区域3 和区域4 的网格数量为20×20。传感器的部署效果如图8 和图9 所示，图中红色、粉色和蓝色圆分别代表探测半径从大到小变化的3 型雷达/可见光/红外传感器的部署位置。如表6 所示，采用PSO-ROM 算法开展重要区域的多频谱覆盖时，雷达波段、可见光波段和红外波段的平均覆盖率分别为91.0%、94.3%和96.1%。在相同任务区域内，在传感器资源覆盖比F 相同的情况下，传感器探测半径越小，传感器数量越多，取得的覆盖率越高。

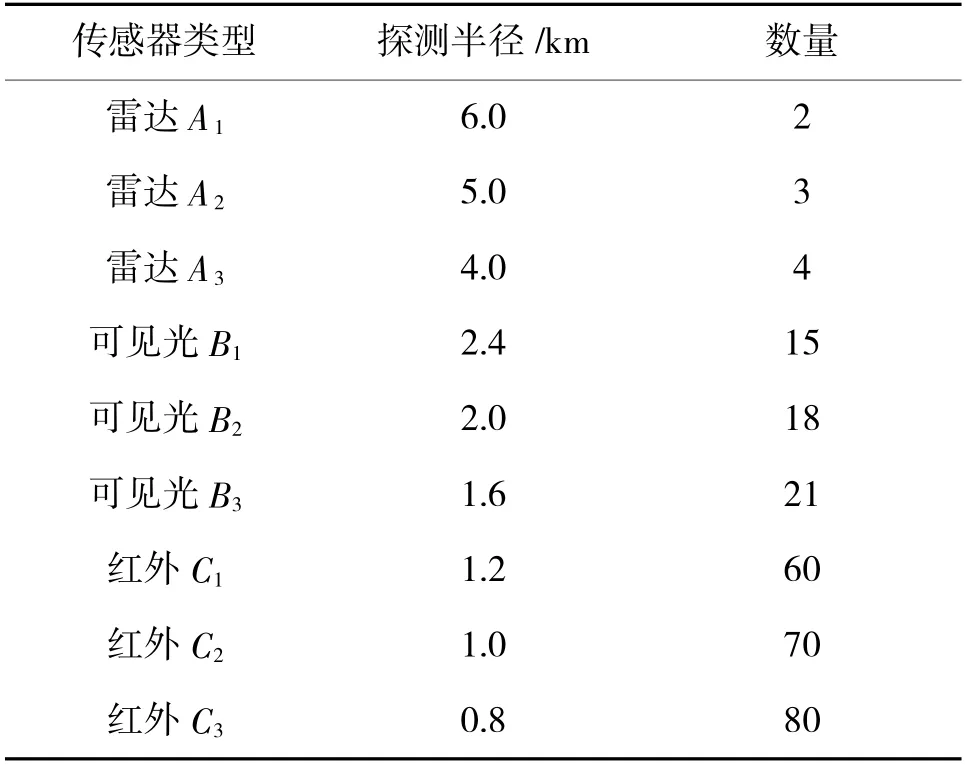
表5 多频谱覆盖中的异构传感器资源列表

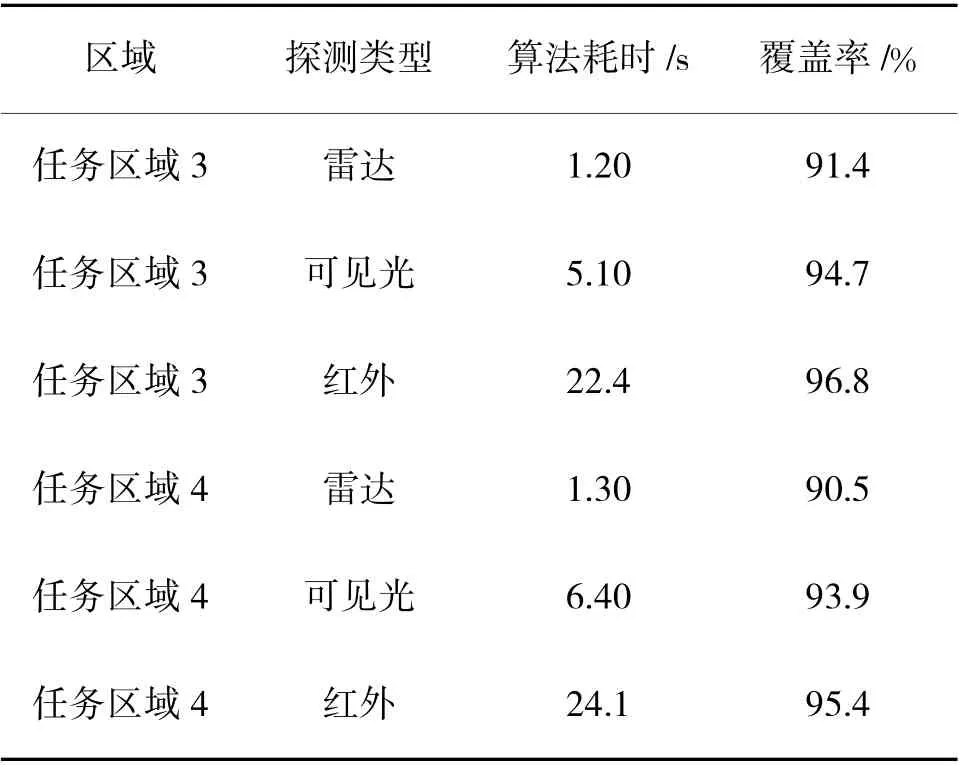
表6 基于PSO-ROM 算法的多频谱覆盖效果

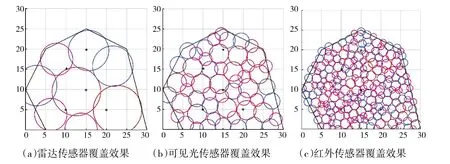
图8 采用PSO-ROM 算法的凸多边形任务区域3 的多频谱覆盖效果

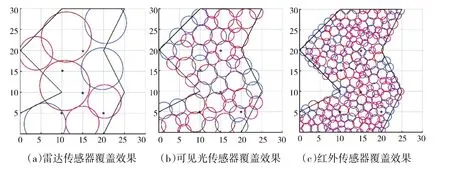
图9 采用PSO-ROM 算法的凹多边形任务区域4 的多频谱覆盖效果

3.3 覆盖比F 对部署效果的影响

为了研究采用PSO-ROM 算法的寻优结果与传感器资源的覆盖比F 之间的关系，如下页图10 和图11 所示，在面积均为550 km的凸多边形任务区域5和凹多边形任务区域6 中，采用PSO-ROM 算法分别对如表7 所示的多型传感器资源（覆盖比F=0.6～1.5）进行覆盖部署。在优化部署中，区域5 和区域6 的网格数量为20×20。传感器的部署效果如图10 和图11 所示，图中红色、粉色和蓝色圆分别代表A、B、C 型传感器的部署位置。不同覆盖比时采用PSO-ROM 算法的覆盖率如图12 所示。

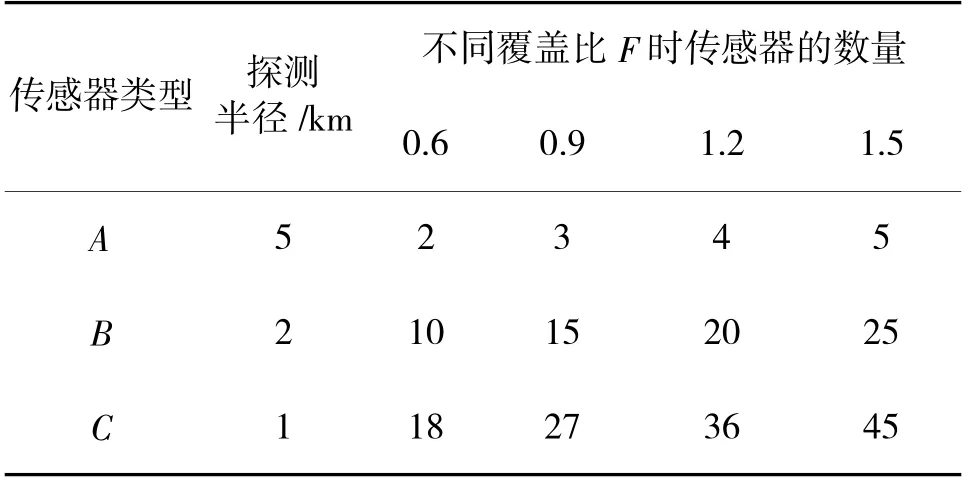
表7 传感器资源不同覆盖比信息表

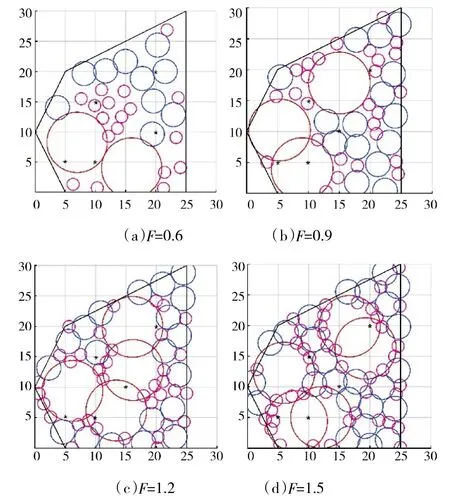
图10 覆盖比F 取0.6～1.5 时，采用PSO-ROM算法对凸多边形任务区域5 覆盖效果

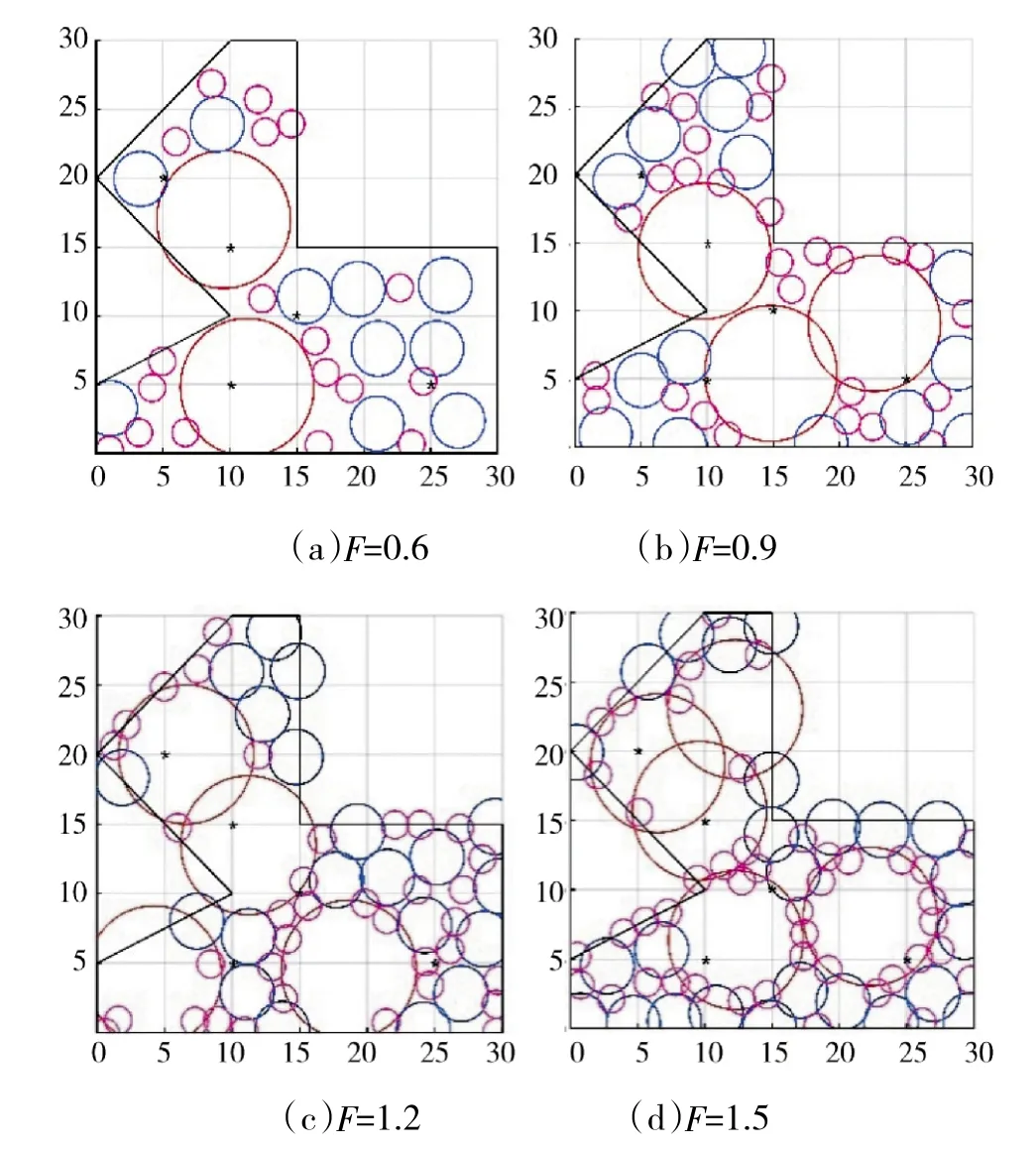
图11 覆盖比F 取0.6～1.5 时，采用PSO-ROM算法对凹多边形任务区域6 覆盖效果

由图12 可知，在覆盖比F 从0.6 增加到1.5 的过程中，传感器的覆盖率从58%逐渐增大到98.5%，且增长趋势逐渐变缓。这是因为覆盖比F 达到1.2时，对任务区域进行部署的传感器资源的利用率已接近饱和，再增加更多的传感器资源将不会对覆盖效果产生明显的影响。因此，在本文对PSO-ROM 算法进行验证的过程中，将覆盖比F 设置为1.2。

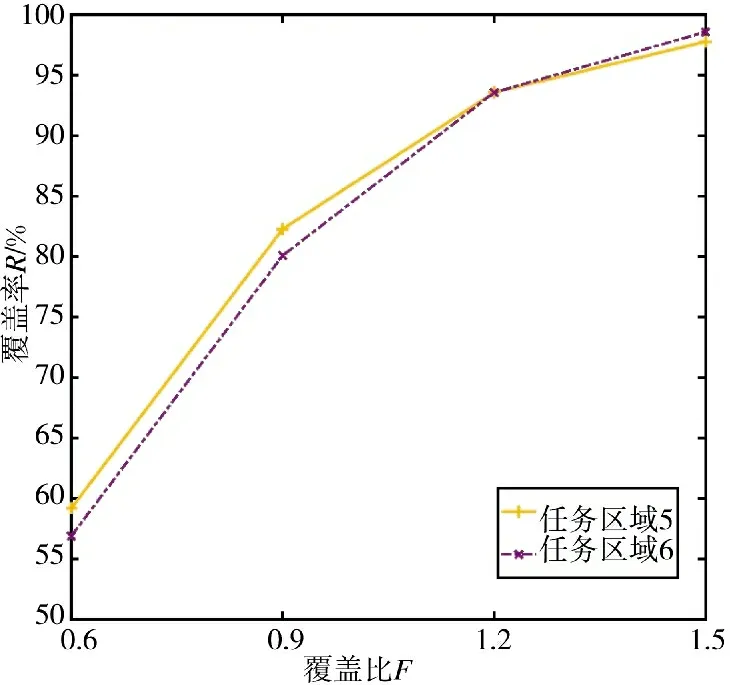
图12 不同覆盖比时采用PSO-ROM 算法的覆盖率

3.4 区域划分网格数量对部署效果的影响

为了研究在寻优过程中，采用PSO-ROM 算法的寻优结果与任务区域划分网格数量之间的关系，在如图10 和图11 所示的凸多边形任务区域5 和凹多边形任务区域6 中，采用PSO-ROM 算法分别对如表8 所示的多型传感器资源（覆盖比F=1.2）进行覆盖部署。在区域5 和区域6 的网格数量由10×10 依次变为100×100 的过程中，传感器的覆盖效果如下页图13 所示，算法的时间消耗如图14 所示。在网格数量由10×10 依次变为100×100 的过程中，传感器的覆盖效果无明显变化，算法的时间消耗按指数增大。这是因为在网格数量增大的过程中，对当前覆盖率的计算更为精确，但是计算的复杂度大幅增加。

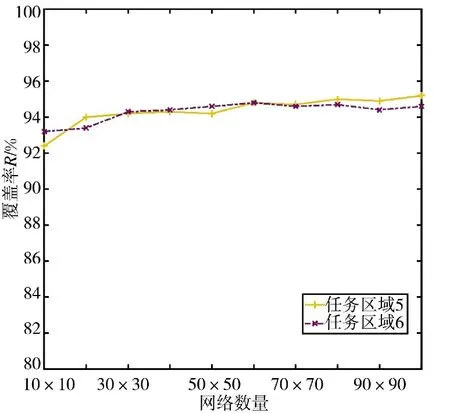
图13 区域划分网格数量对部署效果的影响

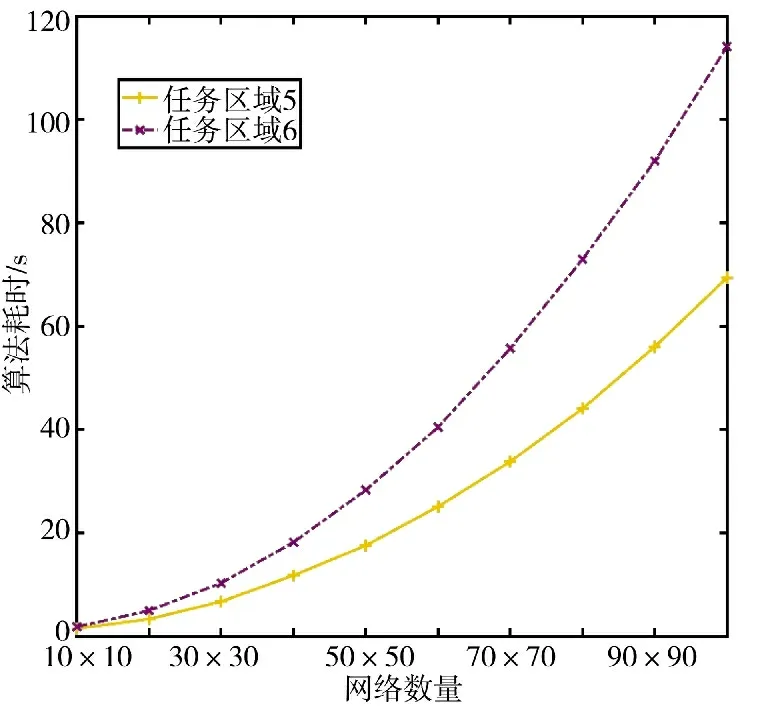
图14 区域划分网格数量对算法耗时的影响

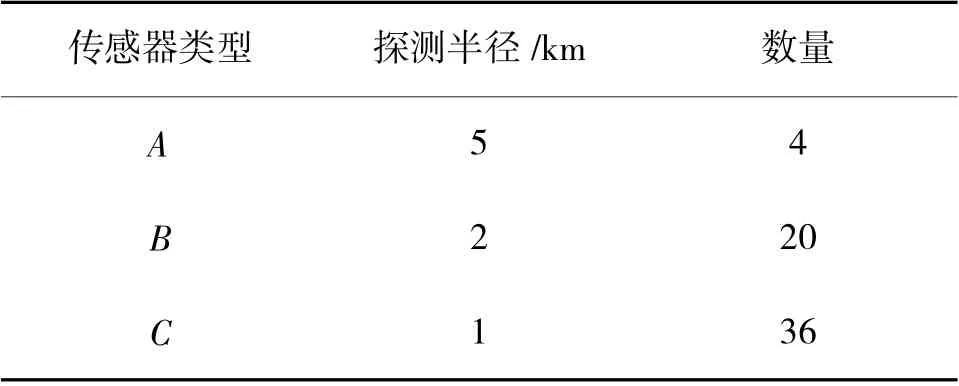
表8 传感器资源信息

4 结论

针对异构多传感器的协同侦察部署问题，本文提出了PSO-ROM 算法。在任意多边形低平起伏与和缓起伏的任务区域内，与传统PSO 算法相比，采用PSO-ROM 算法在显著提高覆盖率的同时，有效降低了算法耗时与节点平均移动距离。采用PSO-ROM 算法开展重要区域的多频谱覆盖时，可见光、红外、雷达等多频段的覆盖率平均达到93.8%。当覆盖比F 为1.2 时，待部署传感器资源的利用率已接近饱和，再增加更多的传感器资源将不会对覆盖率产生明显的改善效果。在任务区域划分网格数量由10×10 依次变为100×100 的过程中，传感器的覆盖效果无明显变化，算法的时间消耗按指数增大。实验结果表明，采用PSO-ROM 算法处理异构多传感器的协同侦察部署问题和重点区域多频谱覆盖问题时具有较好效果。