一种基于线损迭代的超差智能电能表筛查方法

曹 舒，张 颖，魏晓莹，韦先灿

（1. 国网福建省电力有限公司 营销服务中心，福州 350001；2. 福州大学 电气工程与自动化学院，福州 350108）

0 引言

21世纪以来，智能电能表在用电信息采集领域大规模应用，电力行业进入大数据时代。智能电能表计量的准确性关系用户和公共事业服务商的利益，所以在运电能表的误差检测问题备受关注。而传统的人工检测方法已经无法满足大规模的电能表误差检测需求。为此，一些专家学者提出利用电能表历史运行数据，实现电能表误差估计［1］。

近年来，利用大规模电能表数据进行电能表误差分析和估计的研究取得了一些成果，文献［2］—文献［6］介绍了台区线路损耗计算的多种理论方法，通过计算台区线损，可以间接得到电能表误差。文献［7］提出利用系统误差目标函数全局最大化来估计电能表误差，并分别运用两种随机全局极值搜索技术（遗传算法，模式搜索）以及非线性规划求解器来交叉验证被评估解的可靠性。文献［8］从电能计量装置的结构出发，分析了电能表的电压、电流互感器以及二次回路对运行误差的影响，在考虑误差变化的不同因素的随机性和模糊性的基础上，提出了基于云网和动态时间规整的电能计量误差估计新方法。文献［9］提出了限定记忆的最小二乘法计算电能表误差，但是该方法对数据的要求过于苛刻，很难在实际中运用。

综上，虽然在电能表误差估计研究方面已经取得一定的突破，但在实现误差预测的精确性和可靠性方面还有待提高。为此，本文提出一种基于线损迭代的超差智能电能表筛查方法，通过对数据的细粒度划分，筛选出有效的数据来实现电能表误差的精确性估计，最后找到可疑的超差电能表。

1 电能表误差计算模型

1.1 经典计算模型

一个配电台区的电能计量一般由一个总电能表和若干个分电能表组成。传统的异常电能表排查方法是利用在运电能表的历史电量数据，根据电量守恒关系计算分电能表的误差。然后利用所得误差系数找出可疑超差电能表，最后进行现场检定，排除可疑超差电能表。计算模型如图1所示。

图1 电能表误差计算模型Fig.1 Error calculation model of electricity energy meter

在图1中，假定总电能表不存在电量误差，也就是计量值等于真实值，而分电能表可能存在计量误差。台区总电量由总电能表与分电能表电量、各个分电能表之间的线路损耗电量、固定损耗电量构成。其中固定损耗为电压、电流互感器等设备的铁心损耗。对于一个固定的台区，每日的固定损耗可看作固定值。线路损耗与负荷大小息息相关，具有实时性，随着负荷的波动而波动。分电能表电量包括真实电量和误差电量，二者构成了电能表的表计电量。在一个给定的周期内，上述相关量存在以下关系

1.2 模型的改进

公式（1）尽管简单，但存在较多的未知数，单纯使用日电量数据无法准确计算出各电能表误差、线路损耗以及固定损耗。因此，在工程上一般采取忽略线路损耗，使用诸如最小二乘法等参数估计法进行处理。但是这种处理方式，严重影响误差的估计精度，造成误判。本研究推导出一种新的计算模型，将线路损耗纳入计算，以提高误差估计的准确性。由式（1）—式（7）可得

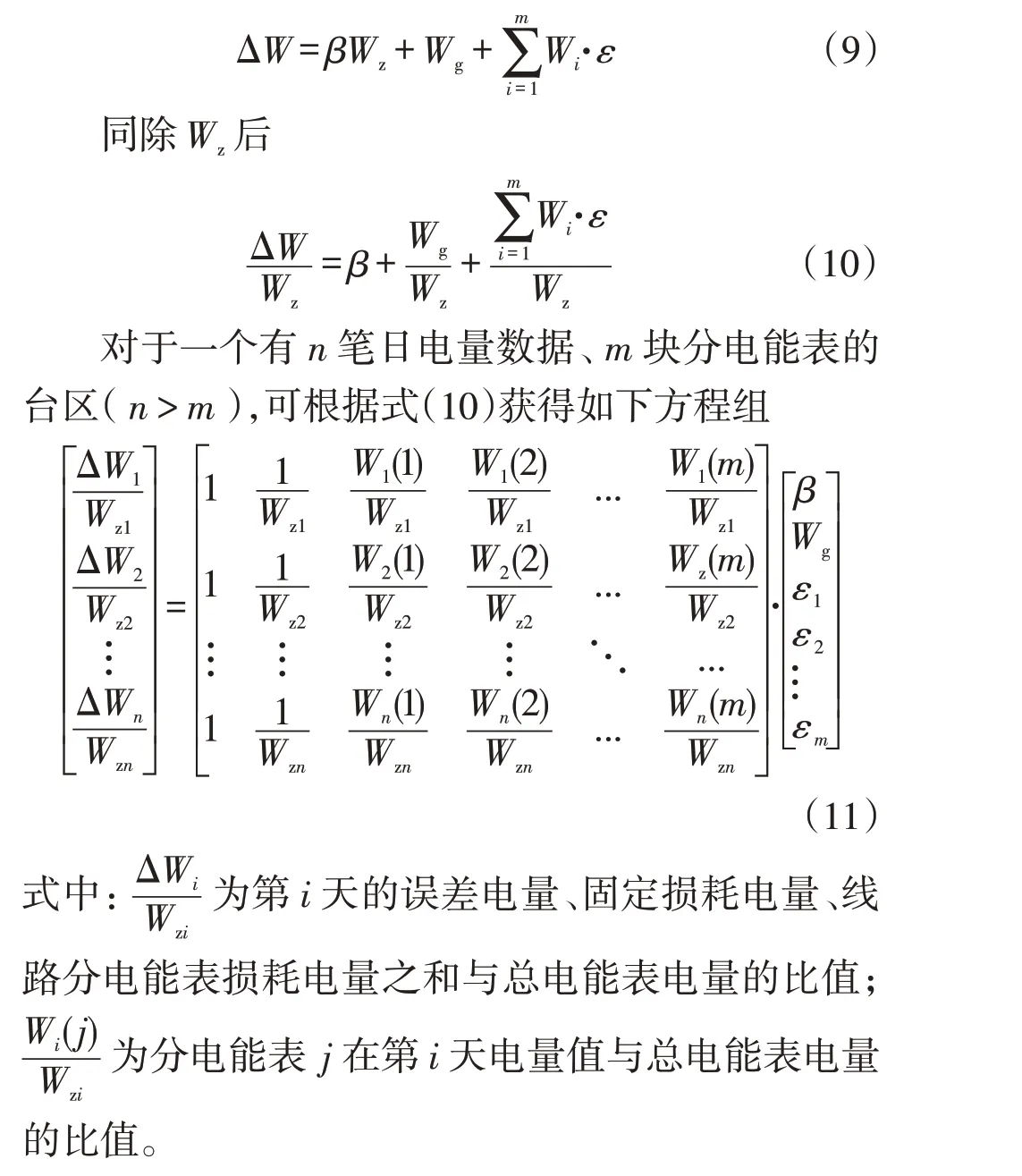
因为用电负荷具有实时性、不确定性，所以同一台区不同时间下的电量数据线性无关。理论上，只要采集的日电量数据大于台区分电能表数，就可以利用式（11）计算出近似误差系数。

2 超差智能电能表筛查方法

2.1 数据标记

电压、电流的波动以及负载谐波会导致电能表的采样电路出现发热、频率特性出现变化，在轻、空载下，电能表的计量误差将出现急剧变大，这些都将可能导致电能表测量值表现暂时性的超差。因此，在计算电能表误差前，需要对这些可能存在误导性的电量数据进行标记，也就是标识出轻载和空载的数据。

数据量较少时，可以使用人工标记的方式进行处理；数据量较大时，可以使用聚类方法对数据进行分类，筛选出轻载、空载和正常负荷三类数据。误差计算时，轻载和空载电能表的数据同样放入计算，当计算结果显示某些轻、空载电能表误差超差，可以忽略计算结果，也就是说轻、空载电能表不被认定为超差表。

2.2 固定损耗、线路损耗计算

在负荷大幅波动的情况下，台区每天的线路损耗都存在变化，而变化的线路损耗将极大的影响计量误差的计算。式（11）所用的线路损耗是固定值，与实际情况相悖。为了使所求结果更为精确，需要计算台区每天的线损值，以便剔除离群线损。定义αWz为总电能表相对误差电量

由前述可知，线损具有波动性，即便台区总用电量相同，不同线损率下差值电量也不相同。由式（12）可知误差电量主要取决于大超差电能表的日用电量大小。若忽略线损，由式（13）可知超差电能表的日用电量大小也会影响差值电量的大小。考虑实际居民用电行为习惯，近似认为具有相同的Wz、ΔW的情况下，其θ的值近似相等。因此，只要挑选合理数据，就可利用式（14）求得Wg。

一般来讲，在目前所设定的电能表检修周期到来之前，台区的超差电能表极少，误差电量占总电量的比重远小于线损电量（即总电能表相对误差系数很小）。换句话说，总电能表误差系数α远小于β，故θ≈β。第i天的含差线损率

据统计，一个台区同时出现两个或两个以上大误差系数电能表的概率很小。若出现一正一负两个大误差电能表，误差电量会相互抵消。这时可根据超差电能表的日用电量大小决定误差电量的大小，也就是挑选出一个误差电能表计量数值较大且另一个误差电能表计量数值较小的数据，来进行误差系数的初步判定，再根据式（16）进行线损修正。

此外，前述的计算过程可以获得配电台区每天线损的分布情况。通过剔除离群线损的电量数据，可使电能表误差系数计算更准确。在此，将剔除规则规定为，去除排序前后δ%的线损数据，保留中间值。

2.3 超差智能电能表筛查步骤

获取电量信息后，进行固定损耗、线损计算，最后形成式（11）方程，紧接着使用迭代寻优进行参数估计，流程如图2所示。j为当前迭代次数、n为总迭代次数、β(0)为预设迭代线路损耗值、W(0)为预设迭代固定损耗值，β(j)、W(j)为第j次迭代计算的线路损耗、固定损耗值，αk为轻载、空载电能表误差系数，αi为分电能表i的误差系数。

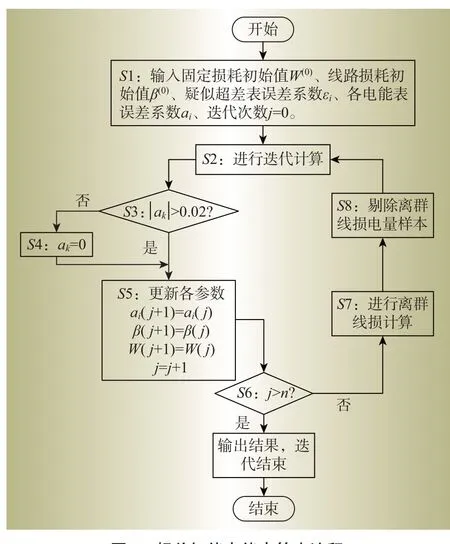
图2 超差智能电能表筛查流程Fig.2 Screening process of out-of-tolerance smart meter

程序执行的步骤如下。

S1：根据数据处理结果设置初始线损、固定损耗和误差系数（判定为疑似超差表的误差系数初值为其估计值，其余电能表初值为0）。可以按照台区的大小预设合理初始线损（一般选取中间值为预设线损），一般来讲，台区拓扑结构越大，预设值也越大。

S2：按照式（11）进行迭代计算，得到第一次迭代计算结果。

S3：对轻载、空载电能表误差进行判断，若判定为超差电能表，则执行S4，否则执行S5。

S4：对第一次迭代所得的空载、轻载电能表误差值进行修正。

S5：更新迭代计算所得的线损、固定损耗以及各电能表误差系数。

S6：对所更新的参数进行判断。若迭代次数超过n次，则输出最终结果。否则执行S7。

S7：利用离群线损判断模型计算各电量样本数据的线损值。

S8：剔除离群电量样本数据，进入新一轮迭代，即继续执行S2。

3 实例验证

3.1 验证分析

使用3个福建省城市居民配电台区的电量数据来验证所提方法的估计效果。台区1、2和3分别有18、85和109台分电能表，3个台区收集的电量数据皆为283天。在计算中，线损剔除边界阈值δ取8，总迭代次数n取3，误差系数大于±2%的表计为超差表。

经过现场人工检测，台区1 和台区2 均为正常台区，即不存在电能表超差；台区3 电能表2 超差。所提算法的判断结果如图3 所示，判断结果和事实相符，并且把台区3的超差表准确筛查出来。

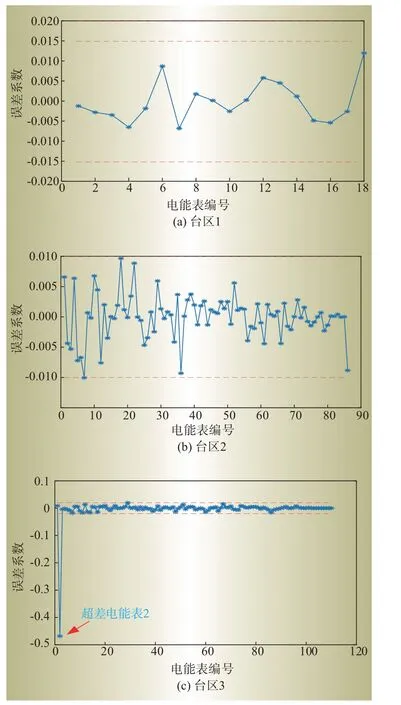
图3 3个台区的电能表误差结果Fig.3 Meter error results for three stations

最后一次迭代完成后，台区1 各个电能表的误差范围在-0.007～0.010之间；台区2各个电能表的误差范围在-0.01～0.01之间；台区3正常电能表的误差范围在-0.02～0.02 之间，超差电能表的误差系数46%。随着分电能表数量增多，误差精度逐渐降低。这是因为随着分电能表数量的增加，求解式（11）所需要的方程数量将增加，所需要的电量样本也要跟着增加。而在本算例中，3 个台区的电量样本数相同，分电能表数逐步增加，因此误差求解精度逐步降低。而通过增加有效的电量样本，可进一步提高大台区电能表的误差计算精度。

3.2 迭代次数对算法精度的影响分析

通过线损筛查来剔除离群数据，可防止有效的数据被误删，提高计算的准确率。但随着迭代次数的增加，有可能会进一步误删有效数据，使精度变低。因此，以台区1和台区3为例，探讨迭代次数对算法精度的影响，不同迭代次数下超差电能表数量统计如表1所示。

表1 不同迭代次数下超差电能表数量统计Table 1 Number statistics of out-of-tolerance meters under different iteration times

图4—图5 分别为台区1、3 的不同迭代次数下的误差分布，从表1 可以看出，随着迭代次数的增加，各台区的误差精度先增大后减小。这是因为随着迭代次数的增加，剔除离群电量样本使数据的线损率相对集中，计算准确度增大。而后，随着迭代次数增加，有效数据也会被剔除。当有效数据不够时，误差精度就会降低。3 个台区中，台区1 多次迭代都未出现超差电能表，计算结果最精确。这是因为台区1 电能表数量较少，求解式（11）所需要的样本数较少。而在输入数据量丰富的情况下，即使删除部分有效数据，也不影响计算结果。台区3 在3次迭代的情况下，可以获得最佳的识别效果。当迭代次数增加，台区3的误检电表数量增加，这是因为迭代删除了一些有效数据，造成台区3 有效数据的缺失，从而使得误差精度显著降低。

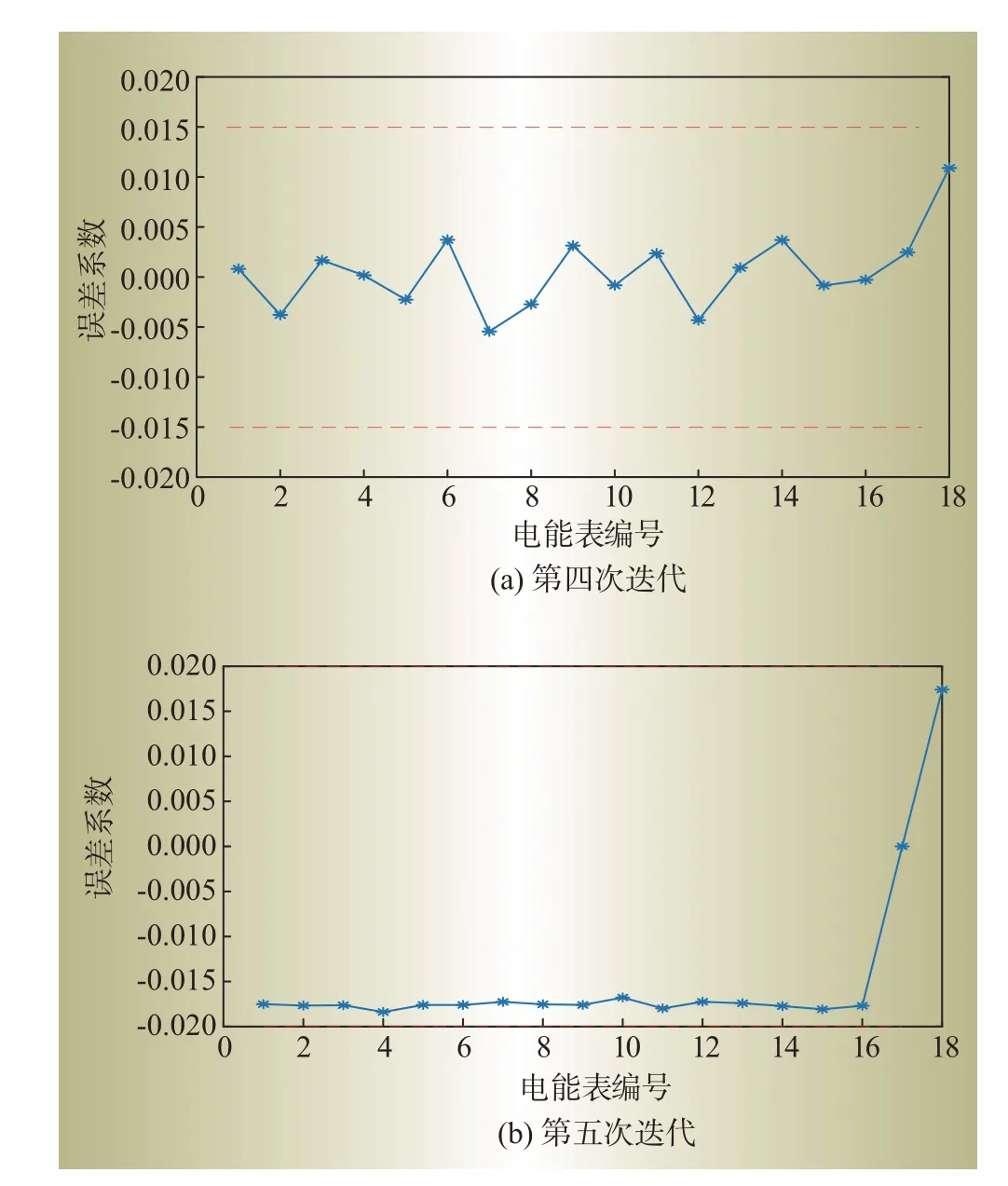
图4 台区1不同迭代次数的误差系数Fig.4 Error coefficients of different iteration times of station 1

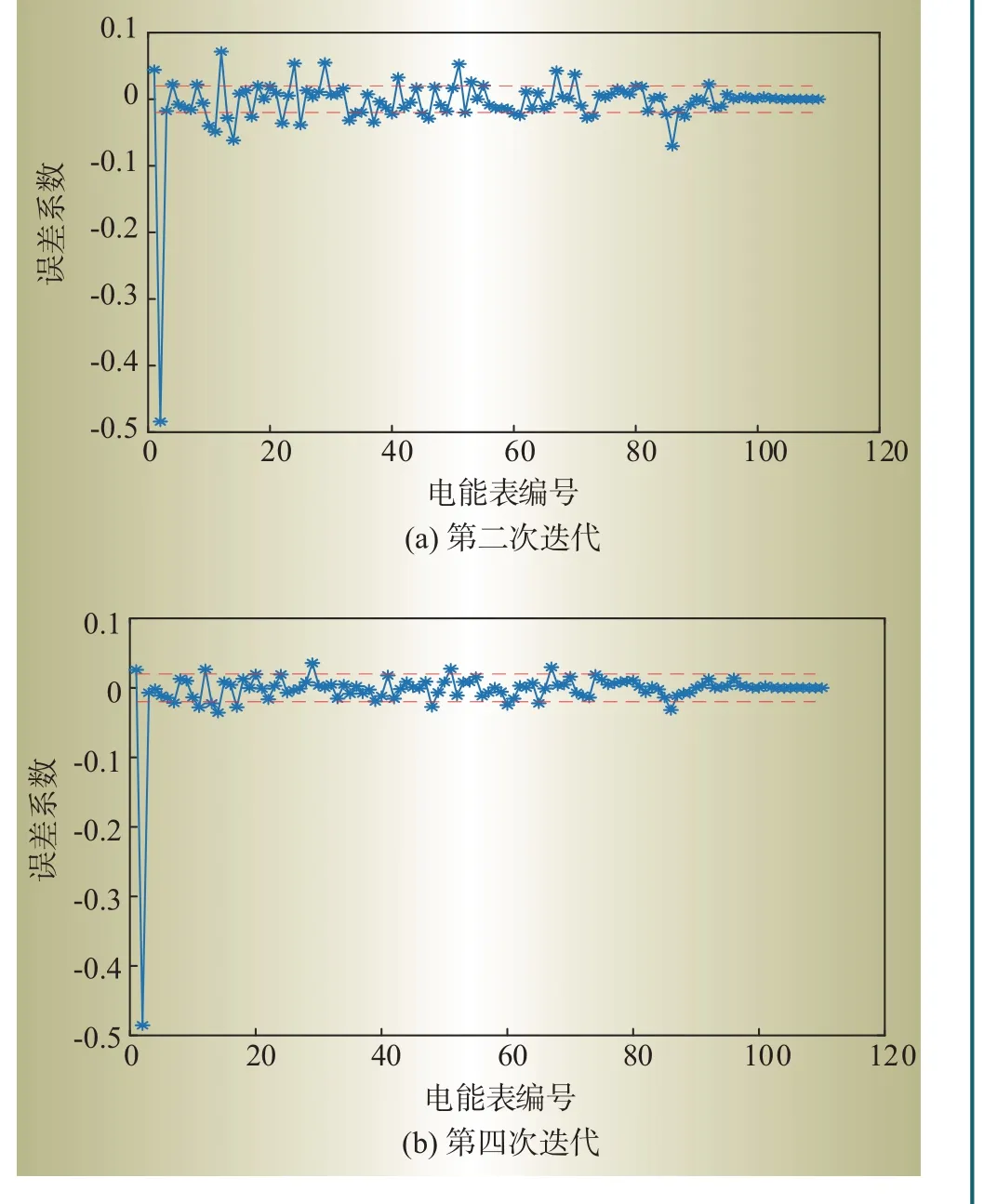
图5 台区3不同迭代次数的误差系数Fig.5 Error coefficients of different iteration times of station 3

3.3 方法对比

为验证本文所提方法的有效性，将其与传统模型的最小二乘法误差估计做比较［10］。评价指标如下

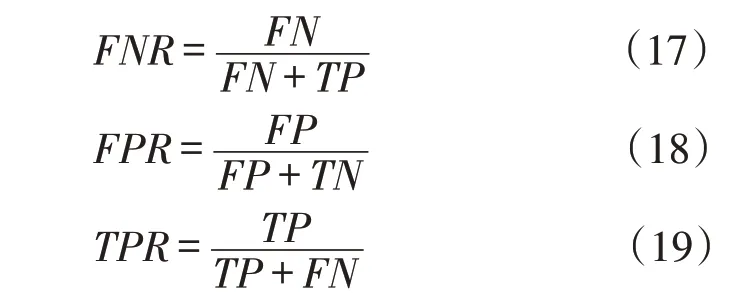
式中：FNR为漏检率；FPR为误检率；TPR为检出率；FP为正常电能表检测为超差电能表的数量；TN为正常电能表检测为正常电能表的数量；TP为误差电能表检测为误差电能表的数量；FN为误差电能表检测为正常电能表的数量。

表2为不同指标下误差计算结果，台区1和2均为正常台区，即没有超差电能表，故不存在漏检率和检出率。可以看出所提方法不仅可以准确检出误差电能表，而且不存在误检其他电能表。最小二乘法虽然也可以正确检测出误差电能表，但是误检率较高。

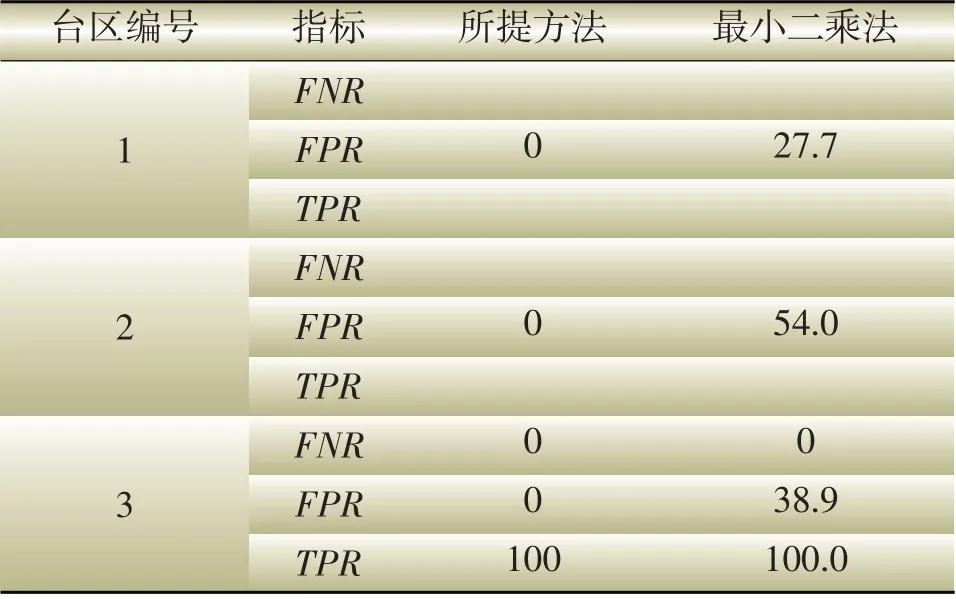
表2 不同指标下误差计算结果Table 2 Error calculation results under different indexes%

4 结束语

本研究提出一种新的超差智能电能表筛查方法，在传统的计算模型上进行改进，加入了线损计算，并运用迭代算法筛选线损相近的数据形成有效样本，解决了电量样本线损不均引起的电能表误差计算不准确的问题。此外，在数据处理时，没有改变电量样本矩阵结构，仅标记空、轻载电能表，排除了空、轻载数据对计算结果的影响，可靠性更高。通过3个不同规模的配电台区算例验证发现，相对于传统的计算方法，所提方法具有更高的精确度。D