计及电动汽车负荷特性的虚拟电厂优化调度

程 熹，洪雅迪，邱辛泰

（国网江苏省电力有限公司 无锡供电分公司，江苏 无锡 214062）

0 引言

随着我国环境治理水平的不断提升，使得风光发电、电动汽车储能等分布式能源不断被加以利用，其中风力、光伏属于可再生清洁能源，但是其发电具有较大的不确定性与随机性；而电动汽车作为储能装置，能够在一定程度上调节风光发电的不确定性与随机性。虚拟电厂通过信息技术聚集了可再生能源发电、电动汽车等分布式能源参与电力市场、电力系统的运行［1—2］。因此如何调度管理这些分布式能源，实现含电动汽车的虚拟电厂（electric virtual power plant，EVPP）收益最大化成为研究热点［2—3］。

国内外学者主要从实现需求响应管理、寻求降低风光出力不确定性两方面开展虚拟电厂的研究。文献［4］考虑用户等可控负荷的需求响应，构建了上层虚拟电厂净收益最大，下层用户用电成本最小的双层随机优化调度模型；基于粗略化的需求响应，文献［5］、文献［6］将需求响应分为基础负荷与可控负荷，并通过LSTM 模型预测用户的需求响应，并求解需求响应系数。在降低风光出力不确定性方面，主要利用随机场景［7］、提高预测精度［8］等方法。上述文献深入研究了接入风光及可控负荷的虚拟电厂参与需求响应，但未考虑电动汽车对其优化调度的影响。

关于电动汽车的研究，主要集中于引导车主有序充放电，具体方法主要是制定峰谷分时电价。文献［9］基于k-means聚类方法划分峰平谷时段，通过划分的峰平谷时段制定分时电价，构建最小化充电费用的有序充放电模型；在分时电价的基础上，文献［10］、文献［11］进一步考虑用户自身指标与所属状态，构建电动汽车有序充放电策略。上述研究均基于额定功率充放电进行策略的制定，未考虑峰谷时段转换带来的“新高峰”问题。

目前关于双目标优化问题的求解，主要有对目标赋权［12］与遗传算法［13］两种方法，其中遗传算法中的NSGA 算法以其寻优效果好频繁被使用，但是存在重要位置无法被识别的缺陷。

为弥补上述研究不足，本文展开计及电动汽车负荷特性的虚拟电厂优化调度研究，主要创新点为：

（1）充分考虑电动汽车负荷特性，考虑电动汽车充放电功率，对其进行约束，由此构建电动汽车的有序充放电策略，避免峰谷时段转换产生的“新高峰”问题。

（2）以EVPP 综合收益最大化与申报偏差率最小化为目标构建EVPP 调度优化模型，充分考虑电动汽车对虚拟电厂产生的影响。

（3）改进现有NSGA算法，引入狮群选择法，解决重要位置无法被识别的问题。

由此，本文首先对电动汽车的时空负荷特性进行分析并结合限制的充放电功率制定电动汽车有序充放电策略；其次以综合收益最大化与申报偏差率最小化为目标构建EVPP 调度优化模型；最后引入狮群选择法求解双目标调度优化模型，并以某一含电动汽车的虚拟电厂为例进行实证分析。

1 考虑负荷特性的电动汽车有序充放电策略

1.1 电动汽车负荷特性分析

电动汽车充放电受车辆类型、充放电方式、充放电时间以及车主自身行为的影响，其负荷特性具有复杂性，当其接入虚拟电厂时，会对虚拟电厂各机组出力产生不确定影响。由此分析电动汽车的时间与空间分布特性，并制定相应的有序充电策略。

（1）电动汽车充电时间分布特性

通过文献［14］可知，电动汽车的充电起始时间服从三峰高斯分布函数，具体如式（1）所示

式中：m为电动汽车的日行驶里程；δp与up分别为标准差与期望值。

电动汽车行驶返回的剩余电量服从正态分布，具体如式（4）所示

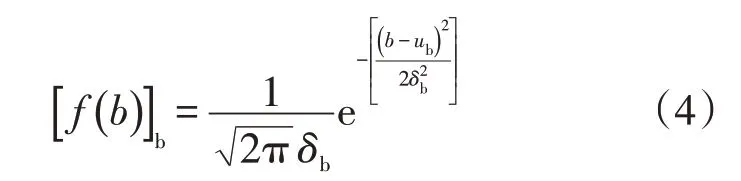
式中：b为返回时所剩余的电量。

1.2 电动汽车有序充放电模型

基于电动汽车的时空分布特性，制定电动汽车有序充放电模型。由于电动汽车返回时间不确定，可分为峰时段返回与谷时段返回两大类。

式中：Q100为驾驶100 km 消耗的电量；Tval为8:00—19:00这一时段；Pcha为额定充电功率；Pe为电动汽车额定的容量。电动汽车日有序充放电策略流程如图1所示。

图1 电动汽车日有序充放电策略流程图Fig.1 Flow chart of daily order charging and discharging strategy for electric vehicles

由图1 可知，电动汽车充放电会根据剩余电量的多少采用不同的策略。

1.2.1 峰时段电动汽车充放电策略

峰时段的情景1为剩余电量大于剩余电量最小值；情景2为剩余电量小于剩余电量最小值。

（1）情景1充放电策略

若剩余电量大于剩余电量最小值，车主先放电，等到谷时段时再充电。

在保证下次出行的前提下，电动汽车在返回时刻放电量最大值如式（6）所示

式中：Qcha_tb为车主i在返回时刻电动汽车的实际放电量；ηdis_tb∈[0,1]为在tb返回时刻的充电参与度；Pˉcha_tb为虚拟电厂为电动汽车车主制定的tb时刻充电价格；f( )Pdis_tb是一个在[0,+∞) 是一个递减函数，且值域为[0,1]，这与参与度的性质完全吻合，充电价格越高，车主的参与度越高。

2 EVPP的调度优化模型

2.1 EVPP运行策略

EVPP 由风光发电机组、燃气轮机、电动汽车构成。EVPP 的出力由风光发电机组以及燃气轮机产生，电动汽车则充当储能设备。首先，通过威布尔分布拟合风速，贝塔-分布拟合光照强度，对风光机组的出力进行预测；其次，根据风电机组与光伏机组的出力预测为电动汽车制定充放电价格，电动汽车则根据充放电价格确定参与度，由此电动汽车的充放电计划行程上报至虚拟电厂调度中心；再次，调度中心根据电动汽车的充放电计划合理确定燃气轮机的旋转备用计划、出力计划；最后，虚拟电厂形成整体的出力计划，在日前市场申报售电量。

2.2 目标函数

从经济性方面选取EVPP的综合收益作为目标函数；从日前市场交易有序稳定方面，选取EVPP申报售电量与实际售电量偏差最小化作为另一函数。

2.2.1 EVPP综合收益最大化

2.2.2 EVPP申报偏差率最小化

EVPP 申报偏差率最小化通过EVPP 申报电量与实际出力差值最小实现

2.3 约束条件

3 改进的NSGA-II算法

NSGA-II遗传算法以其求解速度快、求解效果优被认为是较好的多目标函数求解方法。

传统NSGA-II算法通过非支配等级与拥挤度判断个体优劣情况。非支配等级越高，个体越优；等级相同，拥挤度越大，个体越优。但是个体拥挤度，仅由相邻的两个个体间的差值决定，由此影响最优解的搜寻。图2为不同位置，但是非支配等级与拥挤度相同的情景。

图2 非支配等级与拥挤度相同的情景Fig.2 Scenarios with the same non-dominated level and crowdedness

由图2可知，A、B、C的非支配等级相等，且C的拥挤度由个体A的目标函数值减去B的目标函数值决定，所以，假设ABC 区域中围成的区域中没有个体，从C移动到C1、C2、C3其非支配等级与拥挤度均不会变化，但是C、C1、C2、C3之间的支配关系可知，C1、C2、C3 均由C 支配，所以C 应该比C1、C2、C3 更重要，但传统NSGA-II算法无法识别。NSGA-II算法的基础是生物进化论中的优胜劣汰，由此引入狮群选择法弥补传统NSGA-II算法的缺陷。具体如下：

3.1 初始化种群

狮群选择的基本参数包括狮群规模、狮群个数、种群总规模。其中狮群规模是狮群中的狮子个数，即为优化个体，用IS表示；狮群个数种群中划分的狮群数量，即为优化子群，用IN表示；初始化种群使得种群总规模为种群中的总个体数，用TS表示。同时设置最大迭代次数为Gmax。

3.2 适应度函数确定

由于NSGA-II算法针对的是目标值越小越优的函数，但本文的综合收益目标是越大越优，需对式（15）进行如下式（35）处理，申报偏差率无需进行处理，将式（35）与式（36）作为适应度函数

3.3 进化策略

（1）对指定目标函数值从大到小进行降序处理；

（2）根据确定的狮群规模划分IN个狮群个数；

（3）计算每个个体j的斜率，j=1,2…,TS，具体计算如式（37）所示

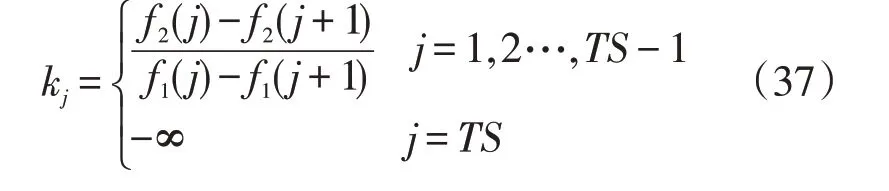
（4）选取斜率小的个体为雄狮，其他个体均为雌狮；

（5）雄狮直接进入父种群，雌狮比较非支配等级与拥挤度两个指标选择最优的雌狮进入父种群。

3.4 交叉与变异

由于EVPP 的综合收益上下界并不确定，采取SBX 交叉算子能够基于步骤（3）父种群得到任意的子种群。再采取边界进行变异操作［16］。

SBX交叉算子如式（38）所示

3.5 最优解输出

判断迭代次数是否达到最大迭代次数Gmax，若达到最大迭代次数，则输出此时的最优个体；未达到则重复步骤（1）—步骤（4），直至达到最大迭代次数为止。模型的具体步骤流程如图3所示。

图3 模型的具体求解流程Fig.3 Specific solution process of the model

4 算例分析

4.1 基础数据

本文以某一实际EVPP 进行实证分析，包含30台1 MW风力机组、5台5 MW光伏机组、2台10 MW燃气轮机组、300辆电动汽车。运行年限为20年，折现率为8%，日前市场允许偏差率为2%，售电价格为0.651 9 元/ kWh。风光机组、电动汽车的基本参数如表1—表3所示［17—18］。风电、光伏机组的出力预测值如图4所示。

表1 电动汽车基本参数Table 1 Basic parameters of electric vehicles

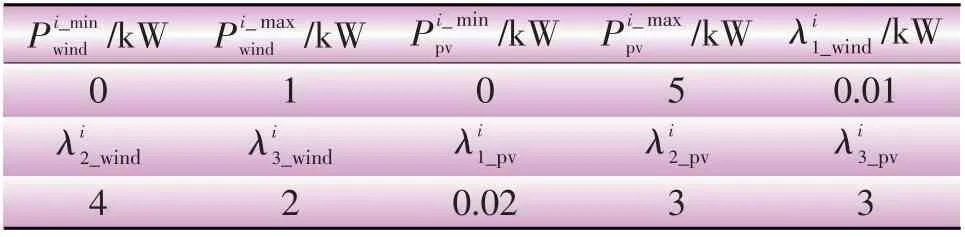
表2 风电、光伏机组基本参数Table 2 Basic parameters of wind power and photovoltaic units

表3 燃气轮机基本参数Table 3 Basic parameters of gas turbine

图4 风电、光伏机组的出力预测值Fig.4 Predicted output value of wind power photovoltaic units

4.2 结果分析

4.2.1 传统NSGA-II 算法与改进NSGA-II 算法对比分析

为了验证所提改进NSGA-II 算法的有效性，同时采取传统NSGA-II 算法与改进NSGA-II 算法对EVPP 的调度优化结果进行分析，设置种群规模为500，狮群规模为25，最大迭代次数为1 000。得到两种算法的优化结果与求解时间如表4 所示，收敛曲线如图5所示，Pareto前沿面如图6所示。

图5 两种算法的收敛曲线Fig.5 Convergence curves of the two algorithms

图6 两种算法的Pareto前沿面Fig.6 Pareto frontier of the two algorithms

表4 算法优化结果与求解时间Table 4 Algorithm optimization results and solution time

由表4 可知，改进NSGA-II 算法目标1 与目标2的优化结果均高于传统NSGA-II 算法，同时改进NSGA-II 算法的优化时间为51.07 s 比传统NSGA-II算法的优化时间59.42 s短。说明改进NSGA-II算法比传统NSGA-II算法求解效率更高。

由图6可知，传统NSGA-II算法比改进NSGA-II算法分布更广，但是传统NSGA-II 算法的左上部分并不连续，且整体来看改进NSGA-II 算法位于传统NSGA-II 算法上方，由此改进NSGA-II 算法比传统NSGA-II算法的优化效果更好，验证了改进NSGA-II算法的优越性。

4.2.2 电动汽车有序充电结果分析

为了验证电动汽车有序充放电策略对电动汽车与虚拟电厂的影响，分别设置如下3种情景。

情景1：电动汽车进行无序的充放电；

情景2：电动汽车进行有序充放电，但不考虑充放电功率限制；

情景3：电动汽车进行有序充放电，同时考虑充放电功率的限制（即本文提出的充放电策略）。

（1）各情景充放电情况

各情景下300辆电动汽车的充放电如图7所示。

图7 电动汽车充放电情况Fig.7 Charging and discharging of electric vehicles

由图7可知，与情景2、情景3相比，情景1的充放电策略显得无序，在13:00时、18:00时处于用电高峰，功率大于0说明在充电，会造成峰谷差增加。情景2虽然遵循着谷充峰放的原则降低了峰谷差，但是由于没有功率限制，电动汽车从谷时大量充电到峰时大量放电，以及峰时大量充电到谷时大量放电变化均特别剧烈，例如从20:00 时放电2 109 kW 到21:00充电734 kW。剧烈的变化一方面会增加电动汽车电池的损耗，降低其使用寿命；另一方面会可能会形成新的峰值。本文提出的有序充放电策略不仅能够减少峰谷差，还能实现电动汽车峰谷时段平稳的变化。

（2）各情景对EVPP的影响

上述3 种情景下对EVPP 成本收益以及申报偏差率的影响如表5所示。

由表5可知，从综合收益角度看，情景3的964.29元＞情景2的704.55元＞情景1的231.72元，这是因为一方面情景1的售电收入低于情景2与情景3，另一方面由于情景1中的电动汽车无序的充放电，使得充放电成本增加，为3种情景中的最高值；情景1中燃气轮机的运行成本也是3种情景中的最高值，这是EVPP提高了备用容量值，为了尽可能降低申报偏差率，弥补电动汽车无序充电行为造成的影响，从而燃气轮机的运行成本增加。至于情景2，由于其峰谷交接处的剧烈变化，导致运行维护成本增加，所以其综合收益低于情景3。从申报偏差率的角度看，情景1 的8.53%＞情景2 的5.92%＞情景3的4.26%，说明在有序充放电条件下能够提高EVPP的综合收益，降低EVPP的申报偏差率。

表5 各情景对EVPP的影响Tab.5 Impact of various scenarios on EVPP

（3）不同规模电动汽车接入EVPP影响分析

为分析不同规模电动汽车接入EVPP是否会对EVPP产生影响，现假设接入的电动车规模从100辆增至1 000辆，不同规模的EVPP综合收益与申报偏差率如图8所示。

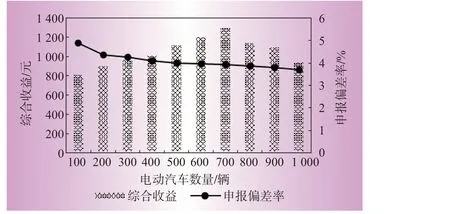
图8 不同规模的电动汽车接入EVPP的影响结果Fig.8 Impact of the integration of EVs of different sizes on EVPP

由图8可知，从综合收益的角度看，电动汽车在100—600辆区间范围，综合收益增加，从600辆起再增加时，综合收益随之降低。从申报偏差率的角度看，随着电动汽车数量增加，申报偏差率随之降低，这是因为随着电动汽车数量增加，通过有序的充放电策略能够弥补一部分风电光伏出力的不确定性，由此降低申报偏差率，使得偏差惩罚成本降低，从而申报偏差率随之下降。但是如果规模持续增加，则电动汽车充放电受车主主观行为的影响会带来一部分不确定性，而且可能会超过配电网的规定容量，从而在接入规模超过600辆后，综合收益降低。

5 结论

本文通过分析电动汽车的时空特性，分析了电动汽车有序充放电策略，并以此为基础构建了以综合收益最大化与申报偏差率最小化的EVPP调度优化模型。为了有效求解双目标优化问题，引入狮群选择法改进了传统NSGA-II算法，并进行实证分析，得到如下结论：①改进NSGA-II算法比传统NSGA-II算法求解效率高，优化效果更佳。②实行功率控制的充放电策略不仅能够减少峰谷差，还能实现电动汽车峰谷时段平稳的变化。③随着电动汽车规模增加，EVPP的综合收益先增加后降低，但申报偏差率一直降低。D