虚拟电厂供电可靠性管理策略研究及评估

陶若冰，徐红丽

（1. 西南交通大学 电气工程学院，成都 610031；2. 中国铁路成都局集团有限公司，成都 610057）

0 引言

环境问题迫使电力行业向清洁能源转型，和传统能源相比，可再生能源如风能、太阳能等在地域上呈分散性，在供能上呈波动性，这些特点给电网运维带来了很大的挑战。为了实现大量分布式能源（distributed energy resources，DERs）可靠并网，需建立更高效的管理平台，加强对系统的实时监控。虚拟电厂（virtual power plant，VPP）依赖软件和通信技术实时对多个DERs 进行协同调度，一方面平抑可再生能源的间歇波动性，另一方面使系统更灵活高效运行，是目前最具潜力的DERs管理平台之一。

DERs 协同控制是提升供电可靠性最有效的方法之一。但目前对DERs提高供电可靠性的研究主要针对单一类型的DERs，比如文献［1］、文献［2］研究提升供电可靠性的储能控制策略，文献［3］分析电动汽车充放电模式对可靠性的影响，文献［4］、文献［5］分析不同需求响应策略和可靠性的关系，文献［6］研究风-光-储协调的微网可靠性问题，但是对DERs综合管理平台如VPP，对配电网供电可靠性的影响还鲜有研究。

由于配电网故障导致网络拓扑结构发生变化，VPP 原有调度策略将不再适用，目前还没有针对配电网故障时VPP 如何响应，以确保系统安全稳定运行的研究。因此本文提出VPP 的可靠性管理策略，包括：①VPP 的运营管理流程，即进行可靠性管理时和其他子系统（如配电管理系统）的信息交换过程；②DERs分组协同优化模型，故障使配电网拓扑结构变化，DERs也因此被分割，对不同部分的DERs分别制定优化策略，以提高供电可靠性并减少由故障引起的经济损失。

同时，为了分析所提出管理策略对供电可靠性的影响，设计了可靠性评估框架。一方面基于已有DERs 对供电可靠性影响的研究，将VPP 对DERs 的协同调度策略纳入可靠性评估中；另一方面，由于VPP 运行高度依赖信息系统，基于已有信息系统可靠性模型，分析信息系统故障对VPP 运行的影响，进而对供电可靠性的影响；最后，利用序贯蒙特卡洛法实现可靠性指标计算。

1 VPP可靠性管理策略

本章基于VPP 结构和功能的介绍，给出配电网故障时VPP管理流程及对DER的协同策略。

1.1 VPP结构与运行方式

VPP利用软件平台和通信技术，协调容量小、地理位置分散的DERs，使他们和传统发电厂一样参与电力市场交易并支持电网稳定运行。其中VPP管理的DERs主要包括可再生能源（风电和光伏）、储能、传统能源（火电和燃气机组）以及需求响应管理。

VPP参与电力市场以及与配电管理系统的协调运行一般可分为两个阶段［7］：

（1）日前调度：VPP根据DERs提供的历史及预测数据，制定次日的交易方案并提交至日前电力市场，电力市场确定并下发VPP最终交易方案；

（2）实时调度：VPP 根据实时DERs、配电网以及市场信息，判断日前调度方案是否需要调整，如需调整将通过参与实时电力市场对日前调度方案进行调整，并在通过配电管理系统安全审核后发送给DERs执行。

1.2 VPP可靠性管理流程和方案

配电网发生故障时，VPP所管理的DERs从物理连接上被隔离成两组如图1 所示。由于这两组DERs 之间不能协同，VPP 对DERs 的原有优化模型将不再适用，因此VPP需切换运行模式。

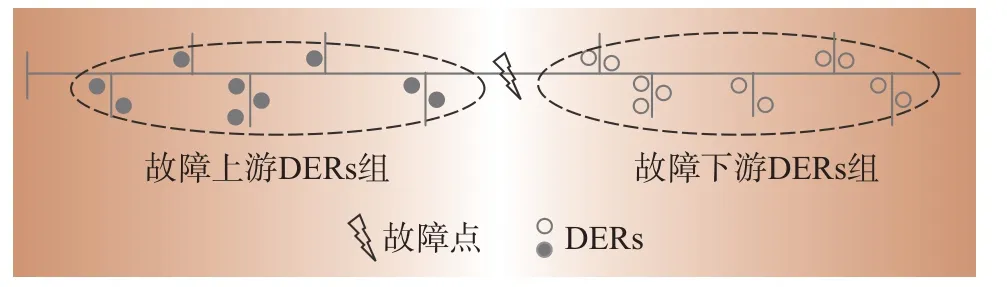
图1 物理系统故障时DERs分组Fig.1 Grouping of DERs during physical system faults

本文定义配电网故障时VPP 的运行模式为可靠性管理模式，切换流程以及信息交换如下：

步骤1：配电管理系统收集并向VPP 发送故障信息和可靠性管理请求；

步骤2：VPP 切换至可靠性管理模式，根据故障信息对DERs 进行分组优化（辐射状网络中故障通常将DERs分成故障上游组和下游组），如图1所示，优化模型见下文；

步骤3：VPP提交更新的DERs调度方案给配电管理系统进行安全审核，如果审核通过则执行步骤5，如果不通过则执行步骤4;

步骤4：VPP 根据配电网反馈的线路电压或容量越限信息，重新调整DERs 出力，重复步骤3 直至通过配电网安全审核；

步骤5：VPP将调度方案发送给DERs执行。

1.2.1 故障上游DER组

配电网故障上游系统在故障隔离后可恢复正常供电，VPP 可协调这部分DERs 参与实时电力市场，从而消纳故障的影响。因此VPP 获取故障上游DERs 信息后，对这部分DERs 建立最大收益优化目标如下

式中：Pl,cap为馈线l的容量；Vn,max和Vn,min分别为节点n处的允许最大和最小电压。

2 考虑VPP的配电网可靠性评估方法

本章首先量化了所提出的可靠性管理策略对供电可靠性影响，其次也分析了信息系统故障对VPP运行以及供电可靠性的影响。

2.1 VPP可靠性管理策略影响分析

大量文献已经建立了DER 的出力模型以及其在上游系统故障时的孤岛运行策略，但考虑VPP时，可靠性评估未应量化VPP 协同调度策略对供电可靠性的影响。由1.2节可知，VPP获取故障信息后重新制定调度方案，在可靠性评估中流程如下：

步骤1：根据故障位置，将DERs 以及负荷点分为故障上游以及故障下游组；

步骤2：利用文献［10］中模型，确定故障时段的DERs出力、负荷需求以及市场电价等信息；

步骤3：利用1.2 节中优化模型确定调度方案，根据切负荷信息计算负荷点可靠性指标，负荷点n的可靠性指标如下

2.2 信息系统故障影响分析

对于信息系统本身可靠性已有较多研究，通常用两种状态模型描述设备故障，用可达性矩阵描述拓扑联通性，通过求取传输时长的概率分布，计算通信时延状态。图2所示为信息系统故障模式。基于已有研究，本文分析了不同信息子系统（Z1、Z2和Z3）故障对VPP运行的影响，以及对供电可靠性的影响。

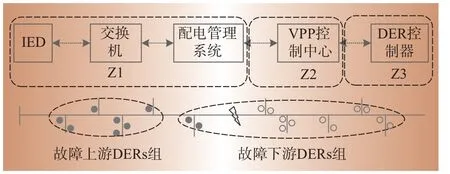
图2 信息系统故障模式Fig.2 Information system failure mode

图2中Z1包含系统主要实现故障定位、隔离和恢复过程的信息传递。物理系统故障时，如果信息故障使故障定位和隔离有误，最终将导致停电区域扩大［10］。由1.2节知，如果配电管理系统向VPP发送不准确的故障信息，VPP据此对DERs的调度结果将导致系统不稳定运行。例如图3中，若VPP根据错误的故障位置信息，将故障上游的DERs划分至故障下游组，则所计算调度策略将不能满足系统约束条件式（14）—式（17），最终造成连锁故障。因此在可靠性指标计算中，VPP管理的DERs均按照停运计入。

图2 中Z2 系统主要实现DERs 调度方案制定，如果配电管理系统与VPP 控制中心通信失效，故障信息将不能传递给VPP，VPP 将按原有方案运行。由于故障时拓扑结构变化会导致原调度方案不能满足系统实际约束条件式（14）—式（17），进而不稳定运行，因此可靠性评估中DER亦按停运计入。

如果VPP 控制中心与DER 控制器之间通信失效，即图2 中Z3 区域故障，VPP 不能获取该DER 的信息，同时该DER 也无法接受VPP 的指令，VPP 将隔离该DER，继续对剩余DERs 进行管理。因此Z3区域信息故障不影响VPP 正常运营管理，但可能影响运行方案的经济性。

2.3 可靠性评估流程

上述VPP 管理策略和信息系统故障对可靠性的影响过程均具动态时序性，因此采用序贯蒙特卡洛法进行供电可靠性评估，算法流程如图3所示。

图3 基于蒙特卡洛法的可靠性评估流程Fig.3 Reliability assessment flow based on Monte Carlo method

3 算例分析

基于IEEE 33 节点搭建算例，结构如图4 所示。VPP共管理8个DERs，其中D1（400 kW）、D5（400 kW）为风电，D2（1 000 kW）为火力发电，D3（200 kW）、D7（150 kW）和D8（250 kW）为燃气轮机，D4（528 kW+200 kWh）为带储能的光伏，D6（225 kW）为光伏。风电运行成本为0.34元/kWh，光伏运行成本为0.43元/kWh，燃气轮机运行成本为0.45 元/kWh，储能的充放电成本忽略不计，火力发电成本为0.56 元/kWh。VPP供应本地负荷电价恒定为0.51 元/kWh，正常工作时每个负荷点均有10%的可切负荷，切负荷成本为0.57 元/kWh。负荷需求、风电和光伏数据详见文献［12］。

图4 基于IEEE 33节点的算例示意Fig.4 Schematic of case study based on IEEE 33 bus

3.1 VPP可靠性管理策略结果分析

通过以下两个场景对本文提出的VPP 可靠性管理策略进行分析：

场景1：物理系统故障发生在母线4与母线5之间，故障发生时段为12：00—15：00；

场景2：物理系统故障发生在母线4与母线5之间，故障发生时段为18：00—21：00。

对应时段的市场电价及负荷需求见表1，VPP可靠性管理策略对DERs的调度结果见表2和表3。为进一步说明本文提出的可靠性管理策略的经济性，将本文调度方案与不考虑VPP管理数据的方案进行对比（表2、表3中括号内为不考虑VPP的数据）。

在图4中，母线4和母线5之间发生故障时，D1、D5和D8属于故障上游DERs组，D2—D6属于故障下游DERs组。场景1中当故障发生在12：00—15：00，负荷需求处于低谷。表2 中对故障上游DERs 组，12：00—15：00 风速较低，风电D1 与D5 出力很少。由表1 知市场电价在12：00—15：00 大于VPP 的本地电价，为避免从电力市场购入更多电量，打开燃气轮机D8 并使其额定出力。此外由于切负荷成本在12：00—13：00时段小于市场电价，因此可以通过切负荷操作来提高运行策略的经济性，但在13：00—15：00 时段切负荷成本大于市场电价，因此尽量避免切负荷。故障下游部分该时段光照充裕且光伏发电成本最低，光伏D4与D6均为最大出力，燃气轮机D3和D7也额定功率运行。最后由于切负荷成本比本地电价高，且为用电低谷时段，因此无切负荷操作。

表1 电价和负荷需求Table 1 Electricity and load demand

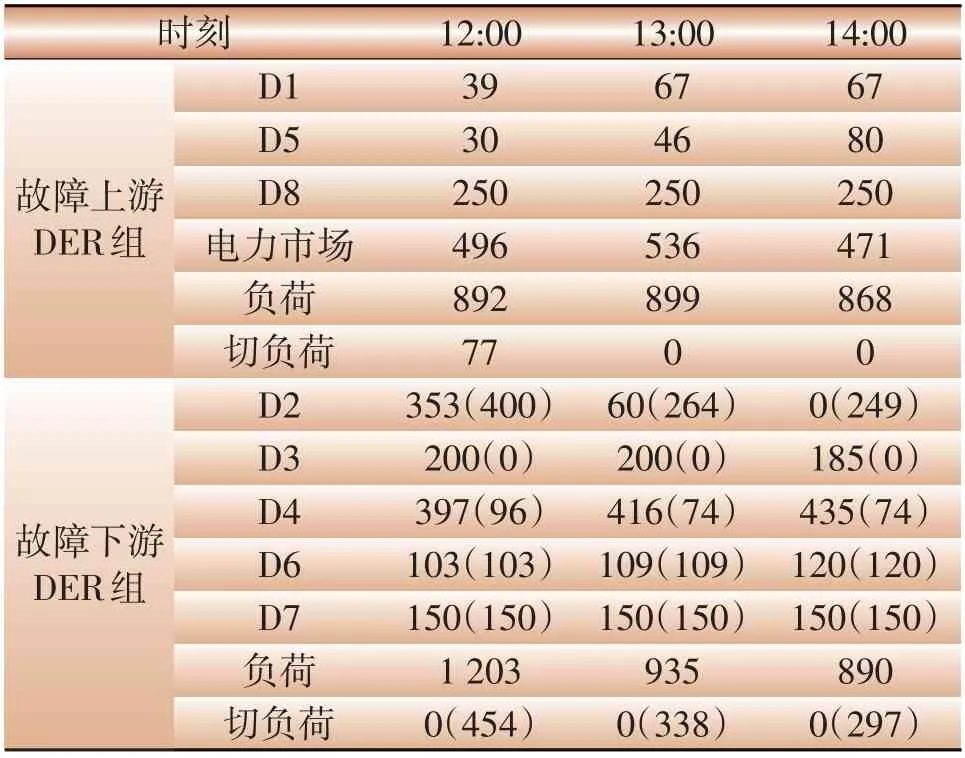
表2 场景1下VPP管理策略Table 2 VPP schedule of scenario 1 kW

场景2 故障发生时段为用电高峰期，如表3 所示。对于故障上游DER 组，风电D1和D5出力依然全部利用，燃气轮机D8 额定出力，剩余负荷需求从电力市场购入，由于此时电力市场电价远高于切负荷成本，因此通过切负荷（最大允许为10%）避免从电力市场购入更多电能；对于故障下游DERs 组，D2、D3和D7均额定功率运行，但此时光伏D4、D6出力很少，由于此时为用电高峰，上述协同策略仍不能完全满足其他负荷需求，因此会导致部分负荷停电。

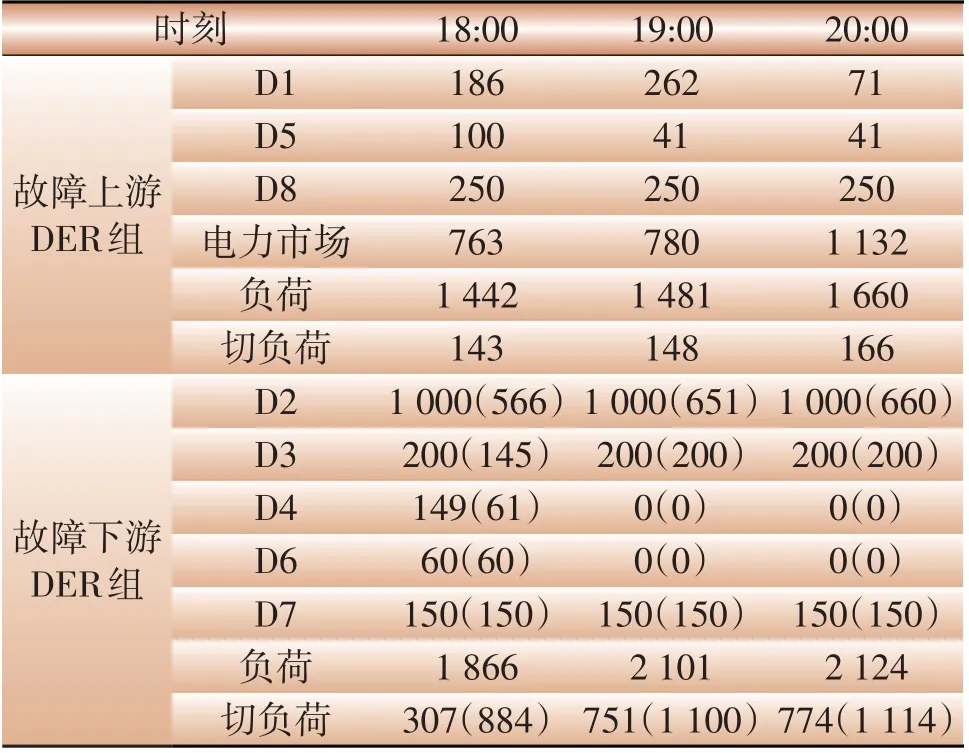
表3 场景2下VPP管理策略Table 3 VPP schedule of scenario 2 kW

对于故障下游，如果不考虑VPP 的优化策略，DERs 按照静态孤岛范围恢复供电。本文根据文献［10］孤岛划分原则，D2 孤岛供电范围为负荷点25—30，D3 和D4 对应负荷点31—32，D6 孤岛包括负荷点7—8，D7 包含负荷点10—12，它们在故障期间不同时段的出力见表2和表3括号。由于静态孤岛划分，没有DERs 之间的协调，因此DERs 的发电策略将会导致更高的运行成本和更多的负荷停电，两种场景中运行成本与本文VPP 优化管理策略的运行成本对比见表4，可知通过VPP优化控制，尤其在负荷低谷期（场景1）可避免下游负荷更多停电，实现更经济的供电可靠性管理。

表4 故障时段运行成本Table 4 Cost during the fault元

3.2 计及VPP管理的可靠性评估结果分析

利用图3 流程对上述算例进行可靠性指标计算，其中物理系统可靠性参数采用文献［11］中数据。序贯蒙特卡洛的仿真时长设置为1 000 a，通过以下3个场景分析VPP可靠性管理策略及信息系统故障对供电可靠性的影响。

场景1：不考虑VPP，利用文献［11］提出可靠性评估方法；

场景2：本文提出的可靠性评估方法；

场景3：本文提出的可靠性评估方法，但信息系统100%可靠。

利用基于蒙特卡洛的可靠性评估算法对上述3个场景进行可靠性指标计算，计算结果见图5。场景1不考虑VPP，当系统发生故障时，故障下游负荷会因为故障隔离而停电，下游DERs切换至孤岛运行模式，恢复部分负荷供电。本文采用文献［10］中方法进行可靠性指标计算。场景2为本文研究场景，即系统发生故障时，故障下游DERs通过VPP协调运行，利用图3所示算法对可靠性指标进行计算。和场景1相比，场景2中通过VPP协调平抑可再生能源的间歇波动性，使故障下游供电恢复更加稳定，此外通过VPP对DERs出力和负荷需求之间的协调，增大故障期间有效恢复供电的范围。因此，场景2 相比场景1 系统平均停电次数（SAIFI）减少11%，系统平均停电时间（SAIDI）和用户平均停电时间（CAIDI）分别减少26%和16%。

图5 供电可靠性指标计算结果Fig.5 Results of power supply reliability

场景3中由于不考虑信息系统故障，即每次物理系统故障，VPP都能协调DERs达到最优故障下游恢复供电，因此，场景3和场景2相比有更高的供电可靠性。图5 中系统SAIDI 减少11%，SAIFI 减少5%，说明在信息物理高度融合的系统中，信息系统对供电可靠性有显著影响。另一方面也表明，确保信息系统可靠是未来提高供电可靠性的重要手段之一。

4 结束语

本文结合VPP运行特性，提出在高比例DERs接入的配电网中物理系统故障时VPP的可靠性管理策略，并在可靠性评估中量化该管理策略对供电可靠性的影响，分析了信息系统故障对VPP运行以及供电可靠性的影响。算例分析可知，本文提出可靠性管理策略能有效减少由故障造成的经济损失，并提高非故障区域的供电可靠性。因此未来对DER综合管理平台的研究方向之一应为多工况下DER的协同优化能力。此外，VPP使信息物理系统耦合加深，信息故障将对物理系统造成更严重的影响，未来需要建立更精细化地信息系统可靠性模型。D