对称构造法解决极值点偏移问题

顾冬梅

【摘 要】 本文是看到近几年高考以及模拟测试中常出现的极值点偏移问题，笔者主要利用对称构造法解决极值点偏移问题，总结了对称法构造解决问题的三步骤，从而感悟化归与转化思想.

【关键词】 构造函数;极值点偏移

极值点偏移问题主要考查导数及其综合应用，涉及函数与方程、化归与转化等数学思想中的难点，这类问题新颖多变，难度较大，综合性强，能较好地考查学生的逻辑推理、数据处理等综合能力，是高考中的热点问题.如2010天津理数21题、2011辽宁理数21题、2013湖南文数21题、2016年新课标Ι卷理数21题、2020、2021年高考中又考查了极值点偏移问题.极值点偏移再次引起人们的关注和讨论，各地的模拟题卷中与极值点偏移相关的问题更是层出不穷.

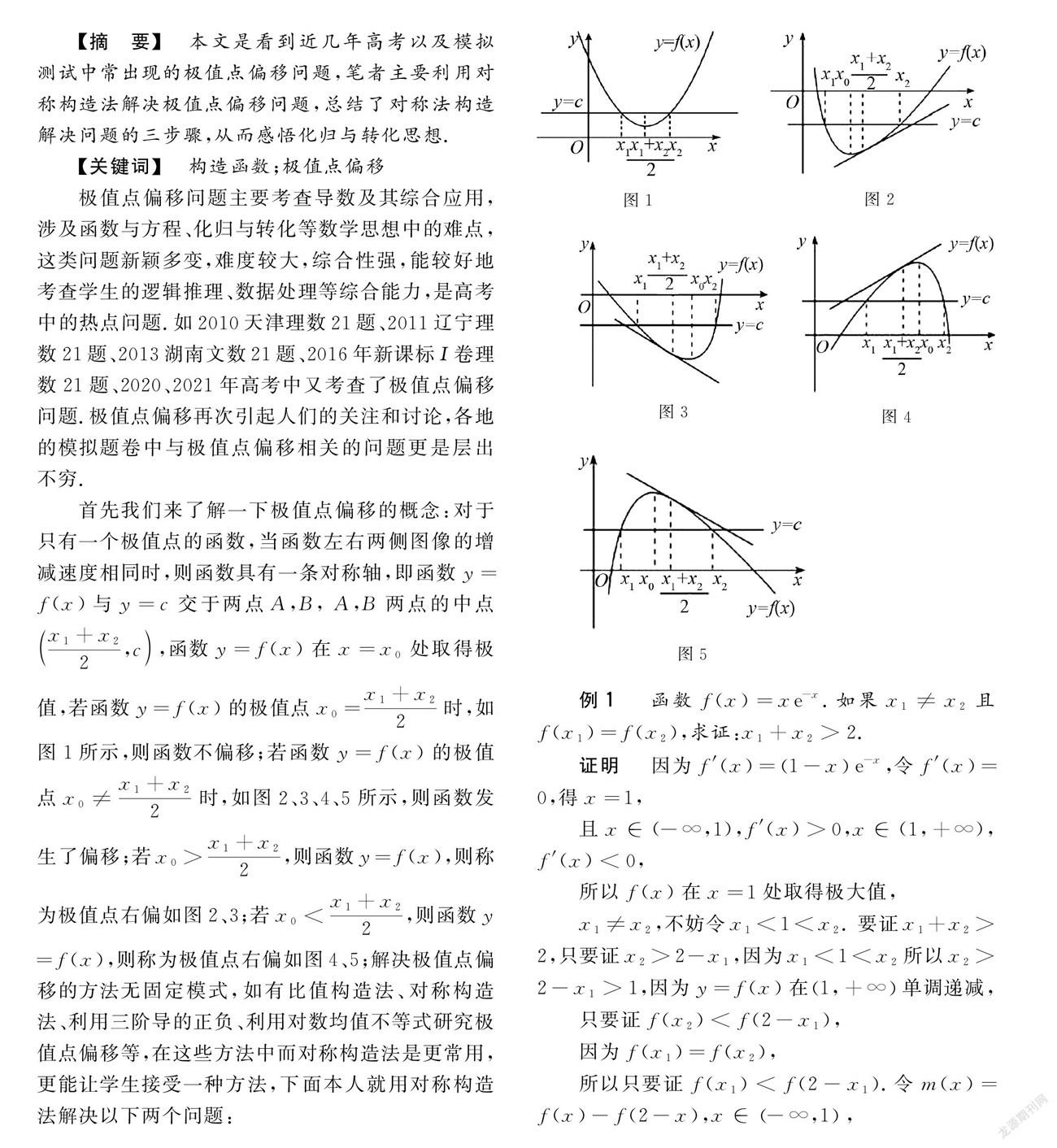
首先我们来了解一下极值点偏移的概念：对于只有一个极值点的函数，当函数左右两侧图像的增减速度相同时，则函数具有一条对称轴，即函数y=f（x）与y=c交于两点A，B， A，B两点的中点x1+x22，c，函数y=f（x）在x=x0处取得极值，若函数y=f（x）的极值点x0=x1+x22时，如图1所示，则函数不偏移;若函数y=f（x）的极值点x0≠x1+x22时，如图2、3、4、5所示，则函数发生了偏移;若x0>x1+x22，则函数y=f（x），則称为极值点右偏如图2、3;若x0<x1+x22，则函数y=f（x），则称为极值点右偏如图4、5;解决极值点偏移的方法无固定模式，如有比值构造法、对称构造法、利用三阶导的正负、利用对数均值不等式研究极值点偏移等，在这些方法中而对称构造法是更常用，更能让学生接受一种方法，下面本人就用对称构造法解决以下两个问题：