“假设法+”在农村小学数学教学中的实践

陈 平

（黎平县中潮镇中心小学，贵州 黔东南苗族侗族自治州 557301）

长期以来，农村小学由于资源不足及配置等问题，一直是我国教育的短板，既影响了农村未来人口素质与当地经济的可持续发展，同时也制约了农村小学课堂教学质量的提高和学生学习的效能。随着社会的快速发展与基础教育的与时俱进，《义务教育数学课程标准》（以下简称《课标》）指出数学教学旨在学生掌握数学基本知识，拓展一般数学思维和积淀数学思想。全面发展经济建设和提高全民素质，基础教育是关键。在理论联系“解决问题”教学实际现状的基础上，我们运用“假设法”为实践策略，尝试解决村小数学“解决问题”课堂中教师“难教”、学生“难学”的问题。

一、农村小学数学“解决问题”教学现状

现今我地农村小学数学教学还是“穿新鞋，走老路”的传统模式。“解决问题”教学的能力普遍偏弱，主要存在如下不容忽视的问题：

第一，教法呆板，脱离实际情境。农村小学条件差，除缺乏相应的科技化辅助性硬件设备外，教师更缺乏“解决问题”教学中抽象“问题”内容生活化的知识能力。

第二，照本宣科，应试为本，忽视拓展多元思维。高学历的年轻“骨干教师和学科带头人”在教学中往往只关注“本本”知识的学习与记忆，以及“高考题海式”应试能力的延续训练，严重忽视了“一题多解”多元思维的培养。

第三，教师基础知识欠扎实，学科知识储备不足，无力挖掘新知与精加工已有知识，未能有效开发、利用农村的优质课程资源，本科第一学历的青年教师尤为明显。

第四，未能准确把握学生年龄特点，“解决问题”教学缺乏解疑导思策略，重结果轻思维，探析过程问题突出。教学中遇到较为复杂的试题只期待“百度”或“试题详解”，脑袋空空，毫无知识积淀。

二、例析“假设法+”在农村小学数学“解决问题”教学的实践

“假设法+”是在假设思维基础上依题意将相关数据与“某方法”组合，将复杂、抽象问题的数量关系直观、浅显、明了化，让问题得到解决，是针对基础薄弱、资源匮乏的村校在数学“解决问题”教学中的实践尝试。当然，探究农村小学数学“解决问题”教学的路径还有很多，在此仅就“假设法＋列表法”列举几例。

（一）虚拟情境的“工程问题”，把整体假设为单位“1”的“假设法+列表法”

［课例1］：这条道路，如果一队单独修，12天能修完。如果二队单独修，18 天才能修完。两队合修，多少天能修完？

教学步骤：①指导学生读题与理解题面，重点是知道两个工程队单独修完各自需要的时间，难点是这条道路究竟有多长？要求解答的问题是“两队合作的工作时间”。②启疑导思，联系之前学过的“工作效率×工作时间=工作总量”公式，已知两队各自的“工作效率”，然后假设这条道路的具体长度，即工作总量。依据题意，运用公式，列表解析如下：

［课练］：一项服装加工出口任务，甲车间独立完成需要8 天，乙车间独立完成需要10 天。如果甲车间先加工4 天，剩下的由甲乙车间共同完成，还需要多少天？

学生在学习［课例1］后，并参照其解题思路，可作表格概析、解答如下：

表2 的解析是这类型题目中学生易于接受的通常解法，教师可引导学生另辟解答该类型题的思路，拓展一下数学思维。如果把甲车间先加工的4 天假设都由甲乙车间共同来做，这时甲乙车间就先做了在表1 和表2 的基础上可作表3 解答如下：

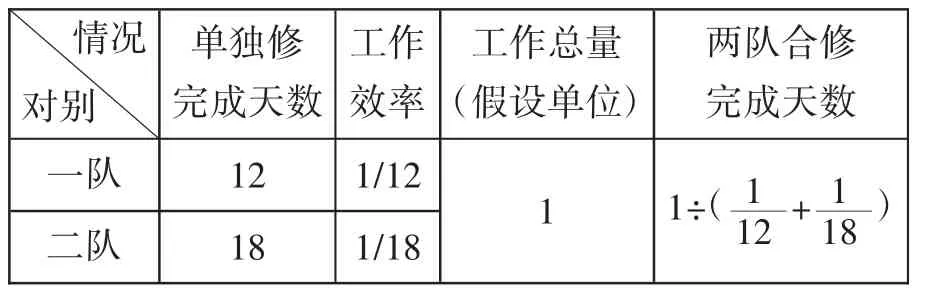
表1

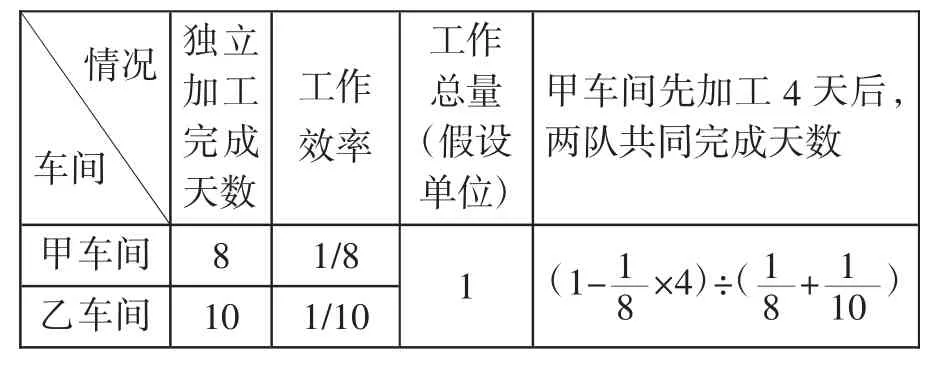
表2

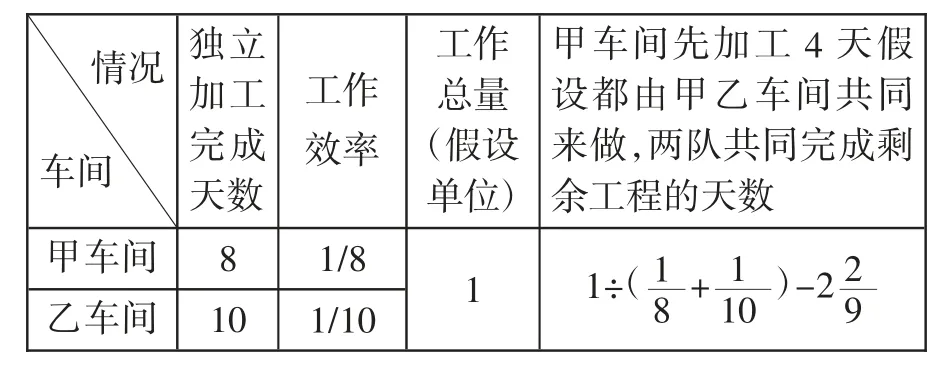
表3

（二）一看就会，一做就错的“行程问题”

这类题目，假设的条件隐蔽较深，表面上看题意浅显、已知条件充分，其实数量关系较抽象，很容易解答错误。需添加辅助性条件，以充当已知数的假设求解法。

［课例2］：一位自行车驴友从山谷骑车到山腰，再从山腰顺原路下到山谷，驴友上山速度是6km∕小时，下山速度是10km∕小时，这位驴友上、下山骑车的平均速度是多少km？

指导过程：①设疑激趣：要求学生尝试解答，学生列出算式“（6＋10）÷2”的错误式子。教师发问：这道题“（6＋10）÷2”这样解答正确吗？②启疑导思：教师引导学生对这道题“（6＋10）÷2”的错误解答展开了讨论，教学过程既突出了学习重点，又能帮助学生突破了用“假设法”解答这类型题目需添加辅助性条件的难点。③解疑展疑：教师可通过直观的“列表”详细分析帮助学生理解。

表4 数据显示：从山谷骑车到山腰的路程不管假设为多少，这位驴友上下山的平均速度均为7.5 km∕小时，依题意可假设山谷到山腰的路程为整体的单位“1”，因此往返的路程就是1×2，驴友上山用时1÷6，下山用时1÷10。依题意得解法：

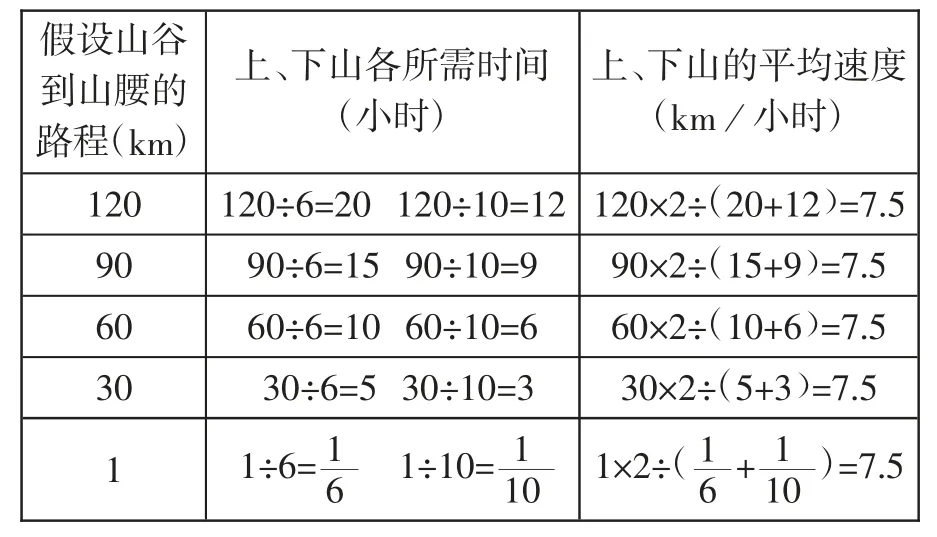
表4

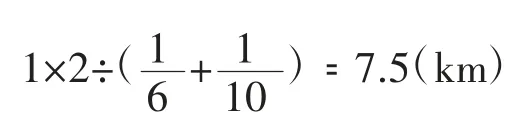
（三）假设问题要求的结果

依题意先设定出一个结果，然后将这个结果和题中已知数量关系进行推理、验算，直至推出满足题设条件的情形，答案则自然显露出来。

［课例3］：一车间有甲乙两生产线共54人。为支援二车间工作，从一车间甲生产线调走的人员，从乙生产线中调走6 人，这时甲乙两生产线所剩人数相等。甲乙两生产线原来各有多少人？

提示：①根据题意假设出甲、乙生产线的人数；②据已知数量关系算出调走人数和剩下人数；③调整、检验至两生产线所剩下人数相等。过程列表如下：

从表5 的数据列举、推理得知，甲生产线原有员工30 人，乙生产线原有员工24 人。

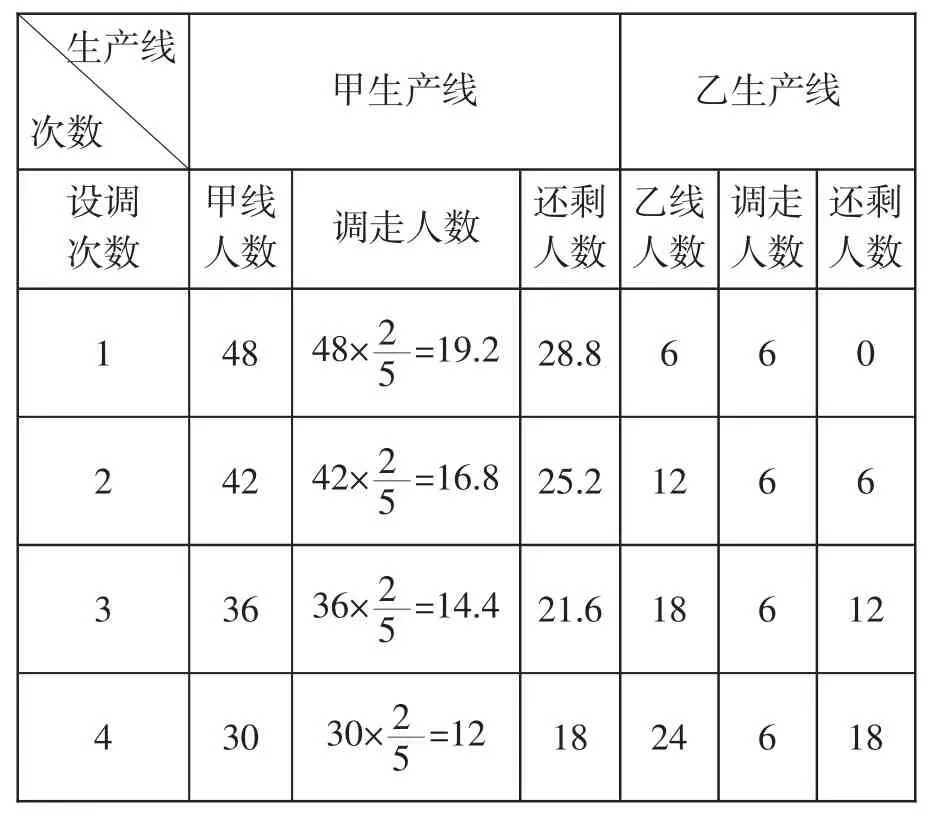
表5

拓展分析：教师还可通过表5 引导学生运用算术解法。一车间总人数减去乙生产线调走的人数，则剩下人数是54-6=48 人。甲生产线调走，乙生产线调走6 人后两生产线所剩人数相等，由此可假设甲生产线为整体单位“1”，则有，于是求出：

（四）“逐步满足条件法”解决一题多解假设问题

问题结果需同时符合多个条件，学生难以把握，可指导学生先暂时放弃某一已知条件，将繁杂问题拆分成多个简单小问题来“兼顾”，逐一击破，然后再整合“统筹”，确定所求结果。

［课练］：两种日记簿，一种软面pv 壳11 元一本，一种塑胶壳8 元一本。陈平花完92 元买这些日记簿，问两种日记簿各买了多少本？

思路一：假设买的日记簿全是11 元一本，依题意列表分析如下：

表6 显示，陈平的钱数全买11 元一本的，买9 本则差7 元，买8 本则多4 元。列式表示：

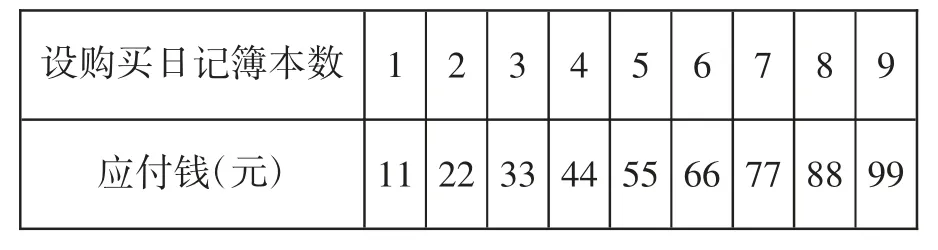
表6

11×9-92＝7（元）………钱不够，差7 元。

92-11×8＝4（元）………钱有余，多4 元。

思路二：假设买的日记簿全是8 元一本，依题意列表分析如下：

表7 显示，陈平的钱数全买8 元一本的，买12 本则差4 元，买11 本则多4 元。列式表示：

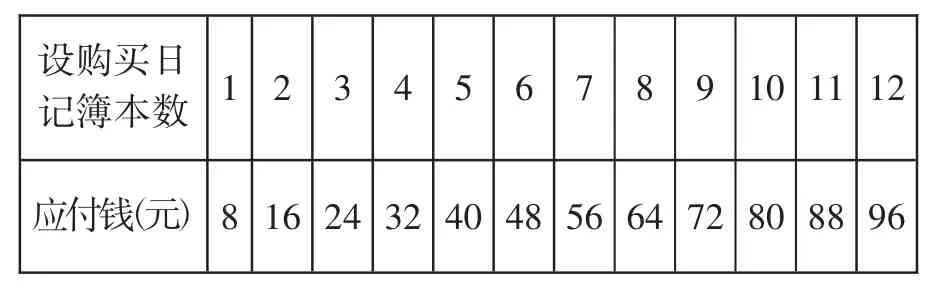
表7

8×12－92＝4（元）………钱不够，差4 元。

92－8×11＝4（元）………钱有余，多4 元。

两种日记簿各买多少本正好用完92 元？从表6、表7 中各找出一个“应付钱”数之和为92及其这两个“应付钱”数对应的日记簿的本数，问题结果自然就解决了。

思路三：假设买11 元和8 元的日记簿本数一样多。列表分析如下：

表8 分析显示，两种日记簿购买本数都是5 本时，则应付钱总数为（11+8）×5=95（元），比实际购买金额92 元超出：95－92＝3（元）。这说明：实际上8 元日记簿比11 元日记簿多3÷（11-8）=1（本）。因此，11 元日记簿应是5-1=4（本），8 元日记簿应是5＋1=6（本）。

表8

三、“假设法+”在农村小学数学“解决问题”教学中的实践意义及“列表法”的局限性

“假设法+”有利于激发学生学习数学的兴趣与欲望，让不同学习层次的学生在思维能力方面得到拓展与提高。小学数学“解决问题”是该学段最为抽象、综合性最强、最富客观实践性的内容知识。鉴于学科本身的特点和应试教育程式地一味题海苦战，忽视了学生对“问题”内容的理解和探究意识的培养，由于农村小学教学硬件设施贫乏，教师教育教学理念滞后，自我学习提升意识模糊，还有长期以来跟班教学模式弊端以及农村学生底子薄弱等因素让学生感到学习数学乏味枯燥，易失去学习兴趣。“假设法+”依据课程教学内容与知识的联系和发展，从学生学习环境的实际状况及其心理特点出发，因地制宜、精心创设教学情境，运用合理的假设与直观明了的列表相结合，充分挖掘教材中“解决问题”的智育因素，突破了单一的传统解题教学模式，培养了学生学习数学的兴趣和主观能动性，进而激发了学生创造性潜能的发挥，拓展了学生的直观形象思维向抽象思维转化，提高了农村小学教学质量，有效优化了农村小学数学教学效果。“列表法”在数学“解决问题”教学中不具有一般性，因为列表法受数据偏大难以穷举、适用题型狭窄的局限而不能广泛运用。

总之，“假设法+”有效挖掘了“解决问题”的价值，拓展了学生数学思维，提高了学生尝试创新的意识，在“假设法+”中巧妙渗透了具体问题具体分析的辩证唯物主义思想和假设思想。以后，我们仍需正视农村小学课堂教学存在的现实问题，以期探索出解决问题的更加行之有效的路径。