行星轮-轴承过盈配合下应力与应变分析

赵紫荆

（重庆交通大学 机电与车辆工程学院，重庆 400074）

据统计，变速箱故障往往是造成风电机组停机时间最长、经济损失最大的原因。运行经验表明，由于行星轮和轴承间微动所引起裂纹萌生、扩展与断裂或接触零部件的表面破坏与形状改变，行星轮系经常出现损伤形态。针对这些问题，沈岗等提出了将行星轮失效过程分为微动磨损和疲劳源产生两个阶段的假设，并对行星轮和轴承间的过盈接触特性进行了分析[1-2]。朱旻昊研究用小球和平板模拟出了径向微动，系统研究了微动的损伤机理，分析了随着循环法向载荷和径向载荷的变化以及径向和周向微动动力学行为[3]。赵俊通过ANSYS软件进行分析，得到了行星轮在不同轮毂厚度、不同过盈量的情况下两者配合面的应力分布和相互间的位移[4]。

本文采用理论分析和有限元分析相结合的形式，对行星轮内表面在和轴承外圈过盈配合时不同过盈量下的应力和应变进行了分析。

1 行星轮系参数及有限元模型

1.1 部件参数

行星轮系的材料性能和几何参数，分别如表1和表2所示[5]。行星轮内圈与轴承外圈的配合公差带为P6，公差为-0.079～-0.047 mm，轴承外圈的公差为-0.035～0 mm，由此可以计算获得行星轮内圈和轴承外圈的过盈量为0.012～0.079 mm。

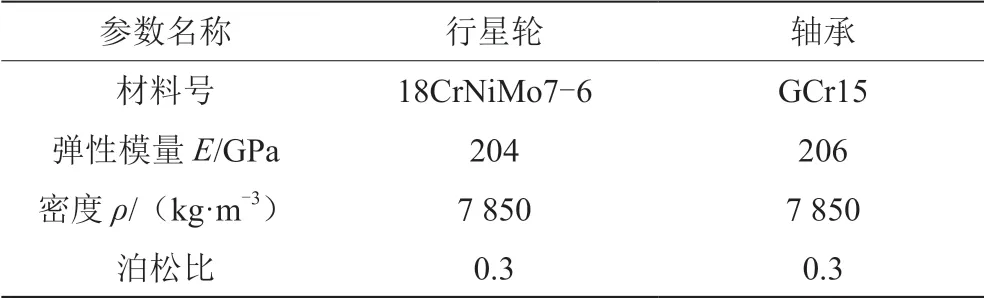
表1 部件材料参数

表2 行星轮系参数

能够对行星轮与轴承过盈配合面造成影响的因素很多，本文仅分析过盈配合量为0.012 mm、0.054 mm、 0.079 mm这3种情况下行星轮与轴承间的应力与应变，不考虑其他影响因素。

1.2 有限元模型

如图1所示，采用六面体网格对行星轮模型进行离散化，并对行星轮内圈和轴承外圈的网格进行加密，共计节点314637个，单元79659个。

2 齿轮轴承过盈接触应力分析

2.1 过盈配合下的力学分析

由于行星轮内圈和轴承外圈的变形为弹性变形，参考文献[6]计算过盈配合面的压强：

式中：p为行星轮内圈和轴承外圈的径向压强；δ为行星轮和轴承间的过盈量；df为配合直径；Ea为行星轮的弹性模量；Ei为轴承的弹性模量；Ca与Ci分别为行星轮和轴承的刚性系数，计算公式如下：

式中：rp为行星轮外径；rf为配合半径；rb为轴承内径；Va和Vi分别为行星轮和轴承的泊松比。

2.2 有限元结果分析

将在SolidWorks中建好的模型导入Workbench，定义两者的材料参数，设置过盈接触，划分网格并施加边界条件，最后得到行星轮内圈不同过盈量下的压强分布如图3所示。

图2为行星轮和轴承的过盈配合示意图，其中df为过盈配合的直径，rb为轴承的内径，rp为行星轮的外径。

在Workbench中提取过盈面平均压强，再与理论值进行对比，如图4所示。可见，两者的计算结果误差在10%以内，验证了有限元模型的可靠性与准确性，可为后续分析不同过盈配合下的变形奠定基础。

3 齿轮轴承有限元分析

3.1 变形分析

在风电机组的实际运行中，行星轮失效的源头是行星轮的内圈。由于行星轮内圈和轴承外圈之间发生了微动，两者间的接触面会产生相应变形。弹性模量就是用来反映材料抵抗变形的能力[7-9]。在生产制造中，比起轴承选用材料的弹性模量，行星轮选用材料的弹性模量要小一些。这就造成在实际工况中行星轮更加容易磨损和变形。

通过配合面压强的理论计算分析和有限元模型进行对比，验证了有限元模型的准确性，接下来可以运用有限元模型分析不同过盈量下行星轮内和轴承的变形量。

如图5所示，可以看出随着过盈量的增加，行星轮和轴承的变形量都在变大，且在不同的过盈量下，行星轮内圈的变形量都是最大的。此外，相较于轴承，行星轮的变形程度更大，这也证实了行星轮相较于轴承更易损伤。

3.2 位移分析

通过对不同过盈量下的行星轮与轴承接触面的应力分析，得到行星轮内表面的位移，如表3所示。

表3 行星轮内圈不同过盈量下的位移

从表3可以看出，伴随着行星轮和轴承之间过盈量的增加，行星轮内表面的径向位移、周向位移以及轴向位移都在不断增加。

行星轮与轴承之间的相对滑动是造成行星轮内表面磨损、疲劳的主要原因[10]。行星轮材料的弹性模量小于轴承的弹性模量，相较于轴承而言，行星轮就是软材料，所以两者间发生相对滑动时行星轮内表面更易磨损。

由表3可知，在静态状况下，随着过盈量的增大，行星轮内表面的轴向位移、径向位移以及周向位移都在增加，沿各个方向的磨损也在增加，因此行星轮更容易造成损伤。

4 结论

（1）通过分析静态不同过盈量下的行星轮内表面和轴承外表面间的应力，采用Lame理论公式计算，并采用有限元仿真与之进行对比，验证了有限元分析的可靠性；

（2）通过对比不同过盈量下行星轮和轴承的变形程度可知，随着过盈量的增加，行星轮和轴承的变形增加，且行星轮的变形程度远大于轴承；

（3）通过分析不同过盈量下行星轮内圈的轴向、周向、径向的位移，定量分析了行星轮静态情况下过盈量越大时更易磨损。