结构光照明下的非相干自干涉数字全息成像

郑梦杰，杜艳丽，黄松涛，刘 星，李朴然，马凤英，弓巧侠

郑州大学物理学院(微电子学院)，河南 郑州 450001

1 引 言

非相干数字全息术，是一种结合全息术、光电技术与计算机技术的高质量成像技术，与传统光学全息术相比在许多方面都存在优势。一方面，它作为一种非相干成像技术，使得任何被非相干光透射或反射的物体、自发光物体都可以实现全息记录，解决了相干成像系统中存在的边缘伪影问题，减少了相干散斑噪声，降低了对相干光源的依赖，提升了成像质量[1-4]。另一方面，作为一种数字全息术，通过图像传感器CCD 或CMOS 等元件代替传统感光材料记录全息图、计算机数值模拟光学衍射过程再现全息图，不仅减少了记录和再现时复杂的处理过程，又可以结合多种图像处理技术来提高再现像质量[5-8]。因此，非相干数字全息术在过去的十几年中从不同的角度得到了广泛的研究，例如三角全息术[9-10]、菲涅耳非相干相关全息术[11-16]、马赫-曾德尔全息术[17-18]、迈克尔逊全息术[19-23]和编码孔径相关全息术等[24-28]。

然而，由于衍射现象的存在，光学系统的分辨率受到数值孔径(NA)的限制，只有物体光谱的低频部分被传输，然后被传感器记录，因此相应的重建图像在频域中是受频带限制的。而且由于没有任何电子设备能够与光学全息术中使用的感光材料的高分辨率(高达5000 lp/mm)相匹敌，所以在大多数情况下，非相干数字全息术实现的分辨率太低，不适合实际应用。目前在数字全息术中已经提出了几种通过增加光学系统的NA 来获得超分辨率成像的方法。第一种是合成孔径技术。2002 年，Massig[29]等人通过平移CCD 到不同位置记录九张全息图，并将它们重新组合成单个数字全息图来增加NA。2006 年，Alexandrov[30]等人通过旋转物体并记录每个位置的数字全息图，使原来大角度散射的光波重新收集到CCD 内，来打破衍射极限。同年，Mico[31]等人提出并演示了一种基于使用倾斜照明和共路干涉记录来提高孔径受限成像系统分辨率的方法。第二种是光栅技术。2002 年，刘成[32]等人证明了可以通过在记录装置中插入衍射光栅，利用光栅的衍射效应将原本落在CCD 之外的高频部分光谱重新导向CCD，以此来获得超分辨图像。2008 年，Paturzo[33]提出了一种利用电光可调二维相位光栅提高数字全息显微系统分辨率的方法，通过在马赫-曾德尔全息装置中插入一个二维六边形相位光栅，提高了图像的二维空间分辨率。2016 年，Kashter[34]通过在SLM 加载正弦光栅实现结构光照明，并成功应用于双透镜菲涅尔非相干相关全息系统(FINCH)。2019 年，宋舒杰[35]等人在FINCH 中采用结构光照明模式，实现了系统轴向分辨率的提高和光学层析成像。在上述研究中，基于CCD 扫描、多光束照明的合成孔径技术的实现一般依赖于高精度的压电陶瓷微位移装置，所需成本较高，而且在实际应用过程中，位移装置易受到外部环境和实验平台震动的影响，导致成像系统出现不规则抖动，从而引起成像系统记录的全息图之间的移位和旋转；而基于SLM的结构光照明技术，只需要在实验装置中加入一个SLM，通过在SLM 上加载不同的掩模，就可以灵活实现不同方向的结构光照明，光路简单，对实验设置要求较低，这些优点使得结构光照明技术在荧光显微、全息成像、三维显示等方面得到了广泛应用[36-38]。

结构光照明技术作为一种超分辨率成像技术，能突破系统的衍射极限，在实现三维超分辨成像方面具有很大的潜力。因此，本文将结构光照明技术与基于迈克尔逊干涉仪的非相干自干涉数字全息成像相结合，提出了基于结构光照明的迈克尔逊非相干数字全息成像系统，期望通过成像仿真和实验来探究结构光照明技术在该系统中横向的良好分辨作用，研究结果可以为高分辨率非相干全息成像系统提供参考。

2 原理分析

结构光照明基于迈克尔逊干涉仪的非相干自干涉数字全息系统如图1 所示。非相干光源经滤光片F 后投射在SLM 上，SLM 上分别加载“1”值的掩模或余弦光栅掩模，以形成均匀光或结构光照明模式，然后经透镜L0成像在物体上。为了将SLM 上显示的图案成像到对比度最大的物体平面上，需要将两个相互垂直的线性偏振器P1和P2放置在SLM 的两侧，偏振方向相互正交。被照明的物体g(r0)上任一点源发出的光，经过分光棱镜BS 后被分为两列光波，这两列光波分别通过透镜L1、L2后，再被反射镜M1、M2反射回BS，经BS 合束后，在CCD 相机平面上发生干涉，形成点源全息图。物体上所有点源全息图的非相干叠加形成了物体全息图。在数字全息记录过程中，物体到L1的距离为zs1，L1到M1的距离为l1/2，L1到CCD 的距离为zh1。物体到L2的距离为zs2，L2到M2的距离为l2/2，L2到CCD 的距离为zh2，其中透镜L1和L2的焦距为f1和f2。

图1 结构光照明基于迈克尔逊干涉仪的非相干自干涉数字全息系统Fig.1 Incoherent self-interference digital holography system based on Michelson interferometer

如图1 所示，在CCD 面的全息图光强分布可以表示为物函数与系统点扩散函数的卷积。当采用结构光照明时，CCD 面接收到的物体全息图可表示为[32]

式中：g(r0)为物体的强度分布；Im(r0,φm)为结构光的强度分布函数；φm为余弦光栅相移值，m为结构光的相移步数，m=1，2，3；“ ⊗”表示卷积。FPSF(r,θn)为系统的点扩散函数，θn为全息图的相移量，n为全息图的相移步数，n=1，2，3。

二维结构光强度分布函数是可分离变量的函数，为了简化分析，只给出结构光的两个方向(x、y)的表达式:

式中：I0为均匀照射的光场强度，是一个常数，本文取I0=1/2；k0为加载的结构光频率。

式(1)中系统的点扩散函数FPSF(r,θn)可表述为

为简化表达式，上式中Q(b)=exp[iπb(x2+y2)/λ]表示二次相位因子，λ为记录光源的中心波长，b为未知量。

在该系统中需要在每一个结构光相移值φm下拍摄三张物体全息图即h1(r,θ1,φm)、h2(r,θ2,φm)和h3(r,θ3,φm)，应用广义三步相移法[19]去除零级项和共轭项后叠加成一个复值全息图为

在频域空间，物体全息图为

式中：k为二维空间频域自变量；Hm(k)、G(k)、Ik分别 表示hm(r,φm)、g(r0)、Im(r,φm)的傅里叶变换；FOTF(k)是光学传递函数，为点扩散函数FPSF(r,θn)的傅里叶变换；δ为单位脉冲函数。G(k)·FOTF表示均匀照明得到的像频谱。像面接收到物体频谱的大小受系统OTF 的限制，若系统截止频率为kcut，则像面频率的范围为−kcut≤k≤kcut。G+1(k+k0)·FOTF和G−1(k−k0)·FOTF表示由于结构光照明引入的物体+1，−1 级高频信息，所以此时像面频率的范围为−(kcut+k0)≤k≤kcut+k0。由于光学成像系统为衍射受限系统，结构光的空间频率k0最大为系统截止频率kcut，最多可将系统空间频率增大一倍。

对于因结构光照明所产生的混频现象，可以采用三相位频谱分离法即取φ1=0°，φ2=120°，φ3=240°(分别对应三张复值全息图的频谱为H1(k)、H2(k)、H3(k))来将三个高低频信息进行分离：

由于频谱G+1(k+k0)·FOTF、G−1(k−k0)·FOTF和G(k)·FOTF的中心位置不在同一点，需要根据傅里叶变换位移定理将其进行移位，得到的正确位置的高频信息：

将G(k)·FOTF，G+1(k)·FOTF和G−1(k)·FOTF进行加权叠加，再进行傅里叶逆变换，得到重建像为

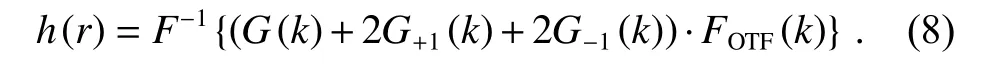
3 成像仿真和实验结果

3.1 成像仿真结果

图2 为成像物体——负USAF1951 分辨率板(2048 pixels× 2048 pixels)，使 用MATLAB 建 立 仿 真系统，设置系统参数为：照明波长 λ=632.8 nm，f1=f2=150 mm，zs1=150 mm，zs2=152 mm，l1/2=222 mm，l2/2=220 mm，zh1=zh2=80 mm，孔径的直径D=1.2 mm，3 张全息图的相移量设为 θ1=0◦，θ2=120◦，θ3=240◦。分辨率板经仿真系统进行成像，得到的结果如图3 所示。

图2 成像物体。(a) 分辨率板；(b) 图(a)中框内的放大图像Fig.2 Object image.(a) The resolution target;(b) The enlarged image in the box in (a)

图3 为基于迈克尔逊干涉仪的非相干自干涉全息系统在均匀光照明下的成像仿真结果。图3(a)～3(c)分别为分辨率板在相移值θn为0°、120°、240°的3张全息图，图3(d)是经过三步相移算法和角谱衍射算法[19]重建后得到的重建图，图3(e)为图3(d)中蓝色框内的放大图像，以便于细节观察和比较。从图中可知：系统可以分辨至第4 组第3 元素，分辨率为20.16 lp/mm。图3(f)为3(e)中第4 组第3 元素的强度分布曲线。

图3 均匀光照明下分辨率板的成像仿真结果。(a)～(c) 分辨率板的三个相移全息图；(d) 重建像；(e) 图(d)中蓝色框内的放大图像；(f) 图(e)中蓝色虚线框内的强度分布曲线Fig.3 Simulated imaging results of the resolution target under uniform light illumination.(a)～(c) Holograms with three phase shifts of the resolution target;(d) The reconstructed image;(e) The magnified image in the blue box in (d);(f) The intensity distribution curve of the blue dashed box in (e)

图4 为基于迈克尔逊干涉仪的非相干自干涉全息系统在结构光照明下的成像仿真结果。具体的实现方式是：首先，按照式(1)将分辨率板图2(a)与空间频率为k0=15 lp/mm 的余弦光栅相乘，即可得到被调制的物体如图4(a1)、4(b1)所示；然后，分别在三个光栅相移值 φm为0°、120°、240°下模拟得到3 张全息图，一共得到9 张全息图。按照式(2)沿着两个方向重复这个过程，总共得到18 张全息图。再利用三步相移法、三相位频谱分离法、傅里叶移位定理、不同级次频谱的叠加，得到的成像仿真结果如图4(c)所示。

当加载水平方向的光栅时，得到重建图4(a2)，从图中可以看出水平方向上能够分辨的最小组是第5组第2 元素，分辨率为35.92 lp/mm，而在竖直方向能够分辨的最小组仍是第4 组第3 元素，分辨率为20.16 lp/mm，水平方向分辨率提高，图4(a3)为4(a2)中第5 组第2 元素的强度分布曲线。当加载竖直方向的光栅时，得到重建图4(b2)，从图中可以看出竖直方向能够分辨的最小组是第5 组第2 元素，分辨率为35.92 lp/mm，而在竖直方向能够分辨的最小组仍是第4 组第3 元素，分辨率为20.16 lp/mm，图4(b3)为图4(b2)中第5 组第2 元素的强度分布曲线。将两方向叠加重构得到图4(c)，从图中可以看出水平方向和竖直方向的分辨率均为35.92 lp/mm，实现了分辨率的提高。

图4 结构光照明下分辨率板的成像仿真结果。水平方向：(a1) 经余弦光栅调制后的物体图像；(a2) 重建图像；(a3) 图(a2)中蓝色虚线框内的强度分布曲线；竖直方向：(b1) 经余弦光栅调制后的物体图像；(b2) 重建图像；(b3) 图(b2)中蓝色虚线框内的强度分布曲线；(c)两方向的重建像Fig.4 The simulated imaging results of the resolution target under structured light illumination.Horizontal direction:(a1) Object image modulated by cosine grating;(a2) The reconstructed images;(a3) The intensity distribution curve of the blue dashed box in (a2);Vertical direction:(b1) Object image modulated by cosine grating;(b2) The reconstructed images;(b3) The intensity distribution curve of the blue dashed box in (b2);(c) The reconstructed image in both directions

从成像仿真结果可以看出：负USAF1951 分辨率板在均匀光照明下系统分辨率为20.16 lp/mm；在频率为15 lp/mm 的结构光照明下系统分辨率为35.92 lp/mm。从而得以证明采用结构光照明相比均匀光照明可以提高成像系统的分辨率。

3.2 实验结果

结构光照明基于迈克尔逊干涉仪的非相干自干涉数字全息系统如图1 所示。被测物体选用USAF 1951分辨率板，非相干氙灯光源(CEL-TCX 250,250 W)经滤光片F (中心波长632.8 nm，带宽10 nm)照明成像系统。P1，P2为偏振器，可将输入光调制为SLM(透射式振幅型1920 pixels×1080 pixels，像素点尺寸8.5 μm)偏振敏感的方向。利用SLM 的可编程特性，加载不同的掩模可实现不同的照明模式，然后经过透镜L0照明在物体上。透镜L0的焦距为60 mm，SLM到L0的距离为120 mm，L0到物体的距离为120 mm。BS 到CCD (2048 pixels×2048 pixels，像 素 点 尺 寸4.54 μm)的距离为95 mm。其他距离设置和模拟系统一致。

在SLM 上加载“1”值的均匀矩阵来实现均匀照明，实验结果如图5 所示。图5(a)～5(c)为不同时刻拍摄的3 张全息图，图5(d)是经过广义三步相移算法和角谱衍射算法重建后得到重建图，图5(e)为图5(d)中蓝色框内的放大图像。从图中可知，系统可以分辨至第5 组第4 元素，分辨率为45.25 lp/mm。图5(f)为5(e)中第5 组第4 元素的强度分布曲线。

图5 均匀光照明下分辨率板的实验成像结果。(a)～(c) 不同时刻拍摄的三张全息图；(d) 重建像；(e) 图(d)中蓝色框内的放大图像；(f) 图(e)中蓝色虚线框内的强度分布曲线Fig.5 The imaging results of the resolution target under uniform light illumination.(a)～(c) Three holograms at different times;(d) The reconstructed image;(e) The magnified image in the blue box in (d);(f) The intensity distribution curve of the blue dashed box in (e)

图6 为基于迈克尔逊干涉仪的非相干自干涉全息系统在结构光照明下的实验成像结果。具体的实现方式是：在SLM 上加载空间频率分别为20 lp/mm，40 lp/mm 的水平、竖直方向的余弦光栅，经过式(6)、式(7)、式(8)的重建算法，得到图6(a1)、6(b1)的分辨率板重建图像。图6(a2)、6(b2)分别为图6(a1)、6(b1)中蓝色框内的放大图像。从图6(a2)、6(b2)中可知：图6(a2)可分辨至第6 组第2 元素，分辨率为71.84 lp/mm，系统理论上的分辨率为75.25 lp/mm；图6(b2)可分辨至第6 组第4 元素，分辨率为至90.51 lp/mm，系统理论上的分辨率为85.25 lp/mm，从而可知实验结果与理论结果较为吻合。

从实验结果可以看出，USAF1951 分辨率板在均匀照明下系统分辨率为45.25 lp/mm；在频率为20 lp/mm 的结构光照明下系统分辨率为64.00 lp/mm；在频率为40 lp/mm 的结构光照明下系统分辨率为90.51 lp/mm。但是从图6(b2)可知，系统分辨率(90.51 lp/mm)却大于系统理论的分辨率(85.25 lp/mm)，这是因为分辨率板不能显示连续的分辨率，成像系统的kcut大于45.25 lp/mm 而小于50.80 lp/mm。从而得以证明结构光照明可以带来成像系统分辨率的提高。

图6 不同频率的结构光照明下分辨率板的实验成像结果。k0=20 lp/mm：(a1) 重建像；(a2) 图(a1)中蓝色框内的放大图像；(a3) 图(a2)中蓝色虚线框内的强度分布曲线。k0=40 lp/mm：(b1) 重建像；(b2) 图(b1)中蓝色框内的放大图像；(b3) 图(b2)中蓝色虚线框内的强度分布曲线Fig.6 The imaging results of the resolution target under structured light illumination of different frequencies.k0=20 lp/mm：(a1) The reconstruction image;(a2) The magnified image in the blue box in (a1);(a3) The intensity distribution curve of the blue dashed box in (a2);k0=40 lp/mm：(b1) The reconstruction image;(b2) The magnified image in the blue box in (b1);(b3) The intensity distribution curve of the blue dashed box in (b2)

4 结 论

我们提出了一种将结构光照明技术应用到迈克尔逊非相干自干涉数字全息系统的新方法。通过在均匀光照明和结构光照明情况下对分辨率板进行模拟成像和实验成像，以提高系统成像分辨率。在仿真成像结果中得出：使用均匀光照明时系统分辨率为20.16 lp/mm；使用结构光照明时系统分辨率为35.92 lp/mm，整体分辨率提高0.78 倍。在实验成像结果中得出：使用均匀照明时系统分辨率为45.25 lp/mm；当使用频率为20 lp/mm 和40 lp/mm 结构光照明时，系统分辨率为64 lp/mm 和90.51 lp/mm，整体分辨率提高0.41 倍和1 倍。综上所述，将结构光照明技术引入迈克尔逊非相干数字全息系统或其他自干涉系统可以显著提高成像系统的分辨率。后续，希望在该研究中结合显微物镜实现系统的超分辨率成像。