频率调制连续波激光雷达测量技术的非线性校正综述

李超林，刘俊辰，张福民*，曲兴华

1 天津大学精密仪器与光电子工程学院，天津 300072；2 天津大学精密测试技术及仪器国家重点实验室，天津 300072

1 引 言

激光的方向性、单色性和相干性都十分出色，是解决精密测量问题的主要光源之一。20 世纪80 年代初，瑞士的Skolnik 提出了调频连续波(FMCW)的理论模型[1]，单模半导体激光器也逐渐得以使用，促使调频连续波技术与激光雷达干涉技术相结合，形成了调频连续波激光雷达(FMCW LiDAR)。在过去几十年的时间里，FMCW 激光雷达技术日趋成熟，调制带宽可以达到太赫兹，测距分辨率提高到微米级，在大气探测、航空航天、三维成像和高精测距等各个领域被广泛应用。图1 是FMCW 技术从2006 年到2021 年的论文发表数量和被引频次统计图，其数据来源于美国科学情报研究所(ISI)自然科学数据库Web of Science 的核心合集和中国科学引文数据库SM，并将文献类型限定为会议、论文、综述论文及在线发表。从统计来看，FMCW 技术越来越成为世界各国研究者们关注的热点领域，而FMCW 激光雷达测量技术更是其中的研究重点。

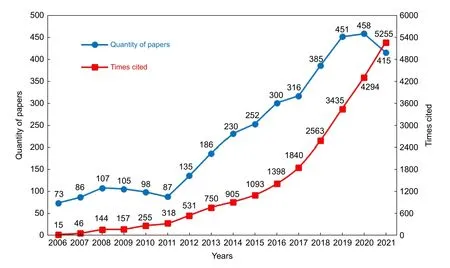
图1 2006～2021 年FMCW 的发文量和被引频次Fig.1 The quantity of papers and times cited of FMCW from 2006 to 2021

FMCW 激光雷达相干测量与非相干测量的脉冲飞行时间法(time-of-flight,ToF)[2-3]和相位法[4-5]相比较而言，具有精度高、灵敏度高、发射功率低、抗干扰能力强、对接收光电子器件的频率要求较低等优势。另外，FMCW 系统非常适合集成光子激光雷达[6]，在很多领域都展现出良好的应用前景。从原理上看，FMCW 激光雷达测距是利用较理想的频率调制激光发射信号和回波信号形成稳定拍频信号来解算待测距离的，所以FMCW 激光雷达测距系统对频率调制的线性度要求十分严格，而实际应用中激光频率的调制不是完全线性的，这在较大程度上限制了测距系统的精度。因此，抑制频率调制非线性的影响是FMCW激光雷达测距系统的研究重点。

为了让读者更好地认识和理解FMCW 激光雷达，本文详细介绍了FMCW 激光雷达的测距方法和研究进展。第2 节简述了FMCW 激光雷达的工作原理；第3 节介绍并分析了各种频率调制非线性校正技术的研究进展；第4 节做出了总结和展望。

2 FMCW 激光雷达基本原理

FMCW 激光雷达测距系统的光源为可调谐激光器，频率调制形式一般为对称三角波或锯齿波，故发射的激光信号是频率以一定周期线性变化的Chirp 信号。测距系统的基本干涉光路如图2 所示，为马赫-曾德尔干涉光路。光源发出的激光经过光隔离器和耦合器后按照规定比例分为两路，分别为测量臂和参考臂。测量臂的光经过环形器和准直镜头发射到被测目标，并且沿着原路径反射回来；参考臂的光经过短的延时光纤。两路光经过另一耦合器合为一路，最终在光电探测器表面发生干涉形成拍频信号，被送入数据采集卡记录。

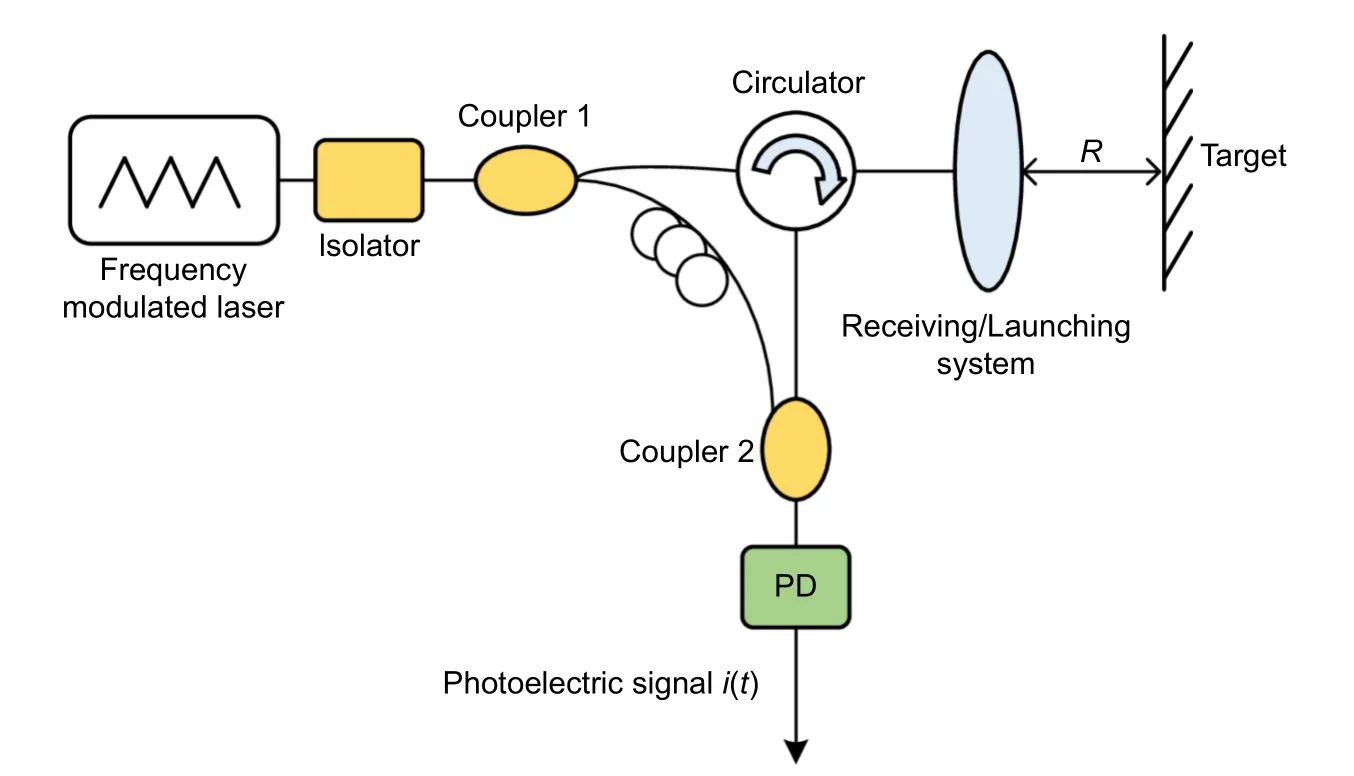
图2 扫频激光干涉绝对距离测量示意图[7]Fig.2 Schematic of absolute distance measurement by laser frequency scanning interference[7]

理想情况下，测量时被测目标保持静止，若激光频率按对称三角波线性调制，拍频形成原理如图3 所示。测量臂和参考臂的光频按相同规律变化，但测量臂(红色)较参考臂(蓝色)在时间上延迟 τ，形成了差拍频率为fb的 拍频信号。该频率fb与待测目标点的距离值成正比关系，据此便可解算出目标距离。

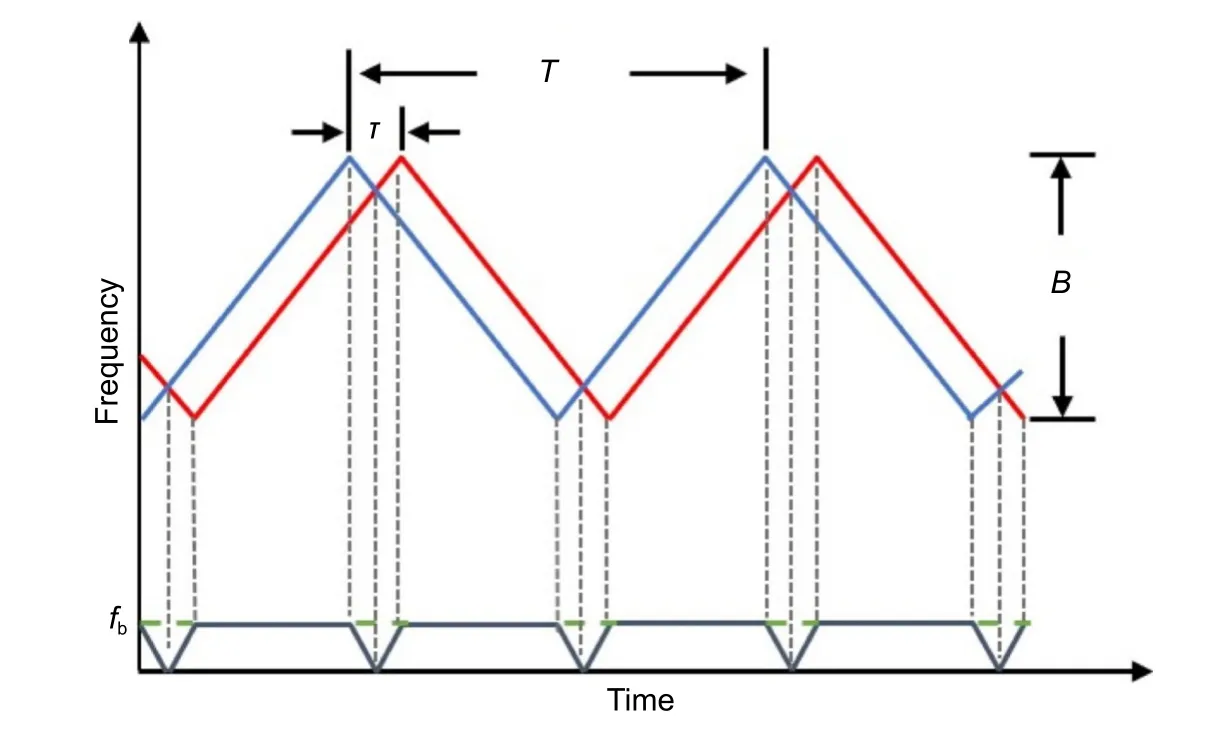
图3 三角波调频激光和静止物体的回波[8]Fig.3 Triangular frequency-modulated laser and echo from stationary objects[8]

下面介绍FMCW 激光测距系统具体的数学原理。出射光频率随时间线性变化，可表示为

式中：f0为调制初始频率，k为调制速率。

出射光信号的瞬时表达式为

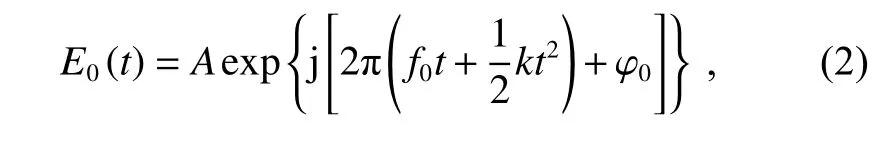
式中：A为 发射信号的振幅，φ0为初始相位。

测量臂的激光经过时间 τ后的回波信号可以表示为

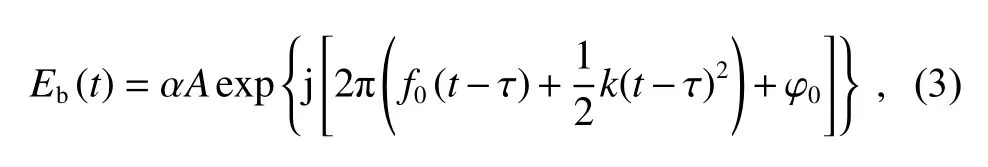
α为幅度衰减系数。

回波信号与出射信号耦合产生拍频，将拍频信号的振幅作归一化，得到表达式：

其瞬时频率为

所以在理想情况下，通过傅里叶变换求取拍频fb，再根据距离公式D=cτ/(2n)得到被测目标距离为

式中：c代表真空中的光速，n代表部分光纤光路和空气的平均折射率，D包括了空气中的距离和环形器等设备引入的距离。

拍频信号由光电探测器转化为电信号，再由数据采集系统采集，而采样频率fs和 采样点数N不可能无限大，所以对拍频信号做离散傅里叶变换后，其频谱分辨率不可能无穷小，应为

在忽略折射率变化和激光器调制线性度的影响的情况下，容易推导出FMCW 激光测距系统的分辨率为

其中：T为频率调制周期，B为调制带宽。由式(8)可以看出，理想情况下的测距分辨率仅与激光器的调制带宽有关，调制带宽越大，测距分辨率越高。当然，FMCW 激光雷达还可以用于速度测量[8-11]和三维扫描成像[12-14]。

3 调频非线性校正技术

在实际应用中，由于激光波长和注入电流之间的非线性关系，电流影响增益介质的温度并导致波长波动[15]以及其他的一些影响，激光器频率调制无法达到完全线性，如图4(a)。调频非线性使得探测到的拍频信号不再是稳定的单一频率信号，其微小波动导致频谱严重展宽，有效频率峰值被淹没而提取失败，如图4(b)和4(c)所示。

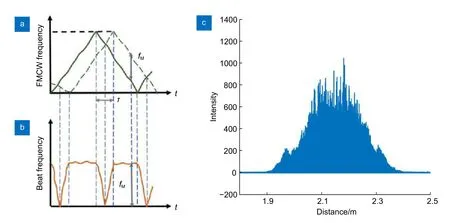
图4 调频非线性对测距结果的影响。(a) FMCW 信号的时频图；(b) 波动拍频信号的时频图；(c) 未经非线性校准的测距信号频谱图[15]Fig.4 Influence of FM nonlinearity on ranging results.(a) Time-frequency graph of the FMCW signal;(b) Time-frequency graph of the fluctuant beat signal;(c) A broadened distance spectrum obtained by FFT on the ranging signal without nonlinear calibration[15]

调频非线性问题是 FMCW 激光雷达测距系统所面临的主要问题，为了解决这一问题，国内外许多研究人员先后提出了不同的解决方案，为这一测量技术的发展起到了积极的推动作用。其中，常用的调频非线性校正技术有锁相反馈控制线性化、等光频间隔重采样法、光学频率梳校正法以及相位比值法，其他还有一些较为特殊的校正方法，下面将对各方法的研究进展进行介绍分析。

3.1 锁相反馈控制线性化

采用主动线性控制技术对激光源进行反馈控制是解决调频非线性问题的一种重要方式。1996 年，Iiyama 等[16]将辅助干涉仪拍频信号通过锁相放大器与一个频率固定的外部参考信号进行相位比较，误差信号被反馈到激光二极管的注入电流中，校正原有的调制注入电流，以此来控制激光的线性调频。在FMCW 反射测量中，扫频速率为 10 ms内 100 GHz，在约16 cm处测距分辨率从原来的12 mm 提高到1.3 mm，调频线性度提高了约 10 dB。2009 年，Roos等[17]基于光纤自外差技术搭建了超宽带激光频率啁啾线性化的闭环锁相测量系统，如图5(a)所示。其外环用于测量和线性度评估，内环用于激光调频线性化。外差拍频信号和稳定的射频参考信号经数字鉴相器比较后，将误差信号据偏差的大小反馈给不同的频率驱动器来保持整个啁啾带宽的相位锁定。为了能实现大带宽调谐的相位锁定，该团队在闭环反馈之前使用希尔伯特变换技术测量了频率非线性，并将计算的所需电压斜坡应用到粗激光调谐元件上。最终，在参数设置为800 ms内 扫描 4.8 THz的情况下，频率线性误差的标准差达到了170 kHz，实现了频率啁啾的精确线性化；在1.5 m范 围内，系统测距分辨率提升至 31 μm，测距标准差高达 86 nm，测量结果如图5(b)。同年，Satyan 等[18]除了搭建运用环路积分器的光电反馈控制回路外，还提出了半导体激光器(SCL)的输入电流预失真技术，如图6(a)所示。将预失真求解的时变电压用于环路积分器的输入，以抑制激光频率调制的非线性，相比于向积分器输入端施加恒定电压，调频速率随时间的变化显著减小；再结合光电反馈控制技术，将频率扫描锁定到频率为2.86 MHz的外部参考信号，在1 ms内 获得了 100 GHz的高度线性光学频率扫描，如图6(b)和6(c)所示。使用该系统进行FMCW 激光测距实验，获得了1.5 mm的距离分辨率，并且该技术还可以扩展到产生任意频率扫描，如二次和指数光学频率扫描。Satyan 团队[19]继续深入研究，在2012 年对光电锁相进行了详细分析，并将负反馈电路与声光移频器(AOFS)结合，实现了垂直腔面发射激光器(VCSEL)在 2 ms内 400 GHz的精确线性频率扫描，其相位误差残余协方差小于0.01 rad2。上述系统的尺寸限制了它们在制造业等领域的应用，高度集成的系统被人们所需要，Beheroozpour 等[20]于2016 年提出了基于芯片级光电锁相环反馈技术的FMCW 测距系统。在按三角波进行调谐时，切换调制方向会导致MZI拍频信号的相位发生跳变迫使EO-PLL 脱离锁定，但是利用切换瞬间与MZI 拍频信号峰值对齐相位跳变最小的机制，可以设计一个选通斜坡开关来抑制该跳变误差，如图7(a)左边的Ramp-Switching Control 部分。该团队搭建了图7(b)和7(c)所示的测距实验装置进行3D 成像，实现了1.4 m 范 围内8 μm 的测量精度。

图5 (a) 使用自外差技术进行宽带光学频率线性化的实验装置；(b) 上图：40 次连续测量的距离误差，误差标准差为86 nm；下图：目标的相对距离测量，以步长为10 μm 移动超过 100 μm[17]Fig.5 (a) Experimental setup for broadband optical frequency chirp linearization using the self-heterodyne technique;(b) Top:range peak centers for 40 consecutive measurements.The standard deviation of the errors is 86 nm.Bottom:relative range measured as the target was manually moved over 100 μm in 10 μm increments[17]

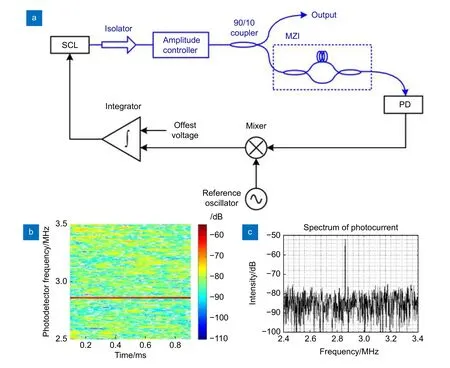
图6 (a) 用于生成精确宽带线性啁啾的光电反馈回路；(b) 环路锁定时环路光电探测器输出的测量光谱图，对应于100 GHz/ms 的光扫描速率；(c) 在1 ms 持续时间内测量的光电探测器输出的傅里叶变换[18]Fig.6 (a) Optoelectronic feedback loop for the generation of accurate broadband linear chirps;(b) Measured spectrogram of the output of the loop photodetector when the loop is in lock,corresponding to an optical sweep rate of 100 GHz/ms;(c) Fourier transform of the photodetector output measured over a 1 ms duration[18]

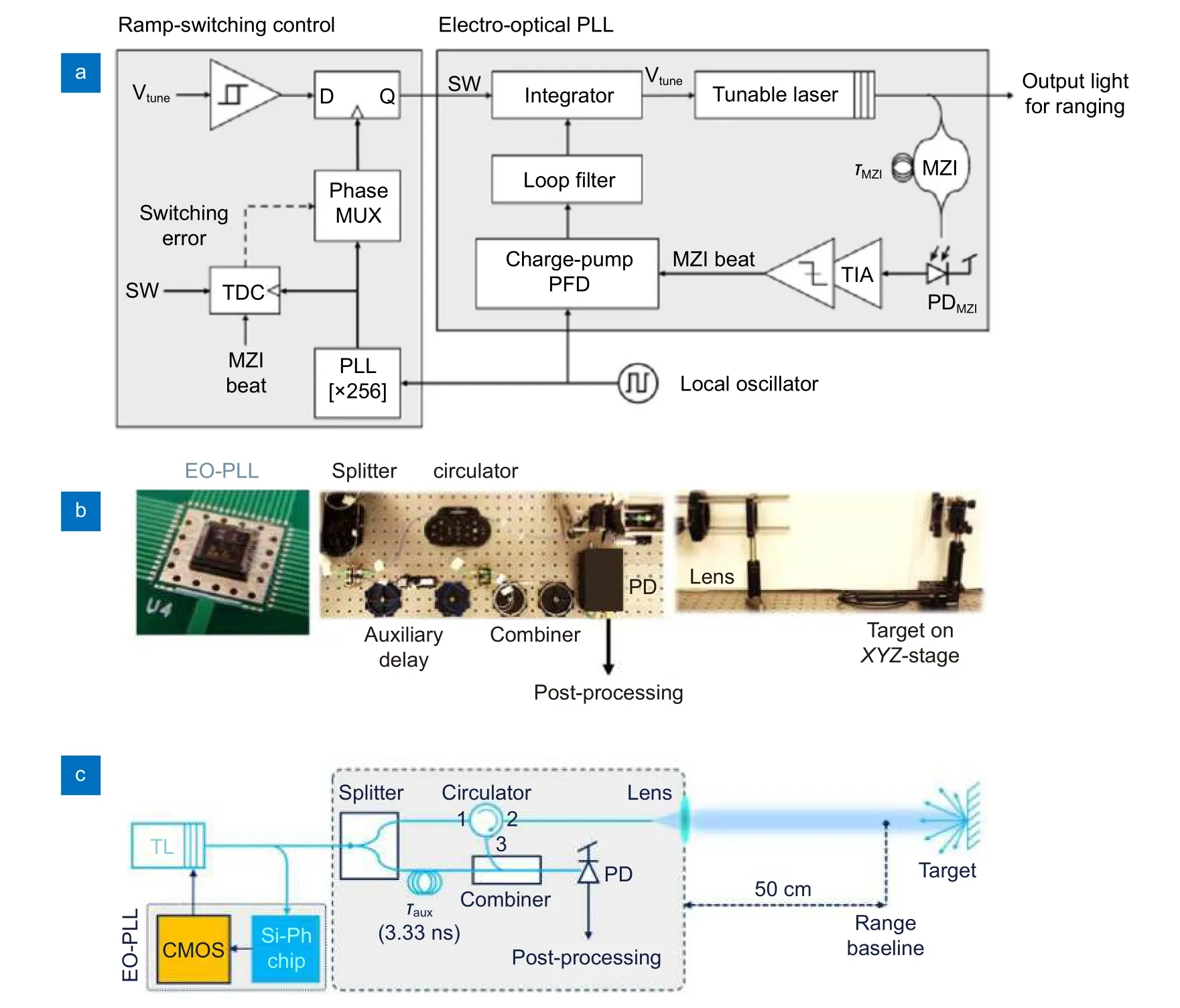
图7 (a) 带门控斜坡切换的 EO-PLL 的详细框图；(b) 测距实验装置的实物照片；(c) 测距实验装置的示意图[20]Fig.7 (a) Detailed block diagram of the EO-PLL with gated ramp switching;(b) Photograph of experimental setup for ranging;(c) Schematic of experimental setup for ranging[20]

在FMCW 激光测量中，调频非线性影响测量分辨率，宽带随机频率噪声影响激光的相干性。2015年，上海交通大学的Qin 等[21]提出了复合反馈回路，如图8 所示，一条回路用于控制DFB 激光器的注入电流，补偿调频非线性，另一条回路用于控制具有快速响应时间的声光移频器的频率，以补偿宽带随机频率噪声。实验结果表明，该复合反馈回路有效地抑制了调频非线性，对于100 ms内 50 GHz的频率调制，残余误差标准差约为89 kHz；同时也有效地抑制了宽带随机频率噪声，增强了DFB 激光器的相干性，获得了更高的信噪比和更大的测量范围，在OFDR 干涉测量实验中，在 处分辨率达到了2 mm，在750 m处分辨率达到了17.5 cm。经过进一步研究，Qin 等[22]在2019 年结合光电锁相环控制和预失真方案，采用外部预畸变压电陶瓷驱动光纤激光器，成功将激光器稳定到全光纤MZI 上，实现了在 200 km 处 0.72 m的空间分辨率。2021 年，Meng 等[23]对复合光电锁相反馈回路进行改进，搭建了由外部AOFS 和内腔PZT组成的双环复合反馈系统，其中，任意波形发生器(AWG)产生的预失真斜坡信号与PZT 环路的误差信号结合使用，以触发频率扫描，从而最小化相位误差并促进锁定过程，并且单独用一个辅助MZI 来监测和评估动态激光频率噪声。实验结果显示，在不牺牲空间分辨率的情况下，实现了瑞利背向散射(RBS)测量范围延长约15 km，在 185 km处 得到了 3.7 cm的空间分辨率。

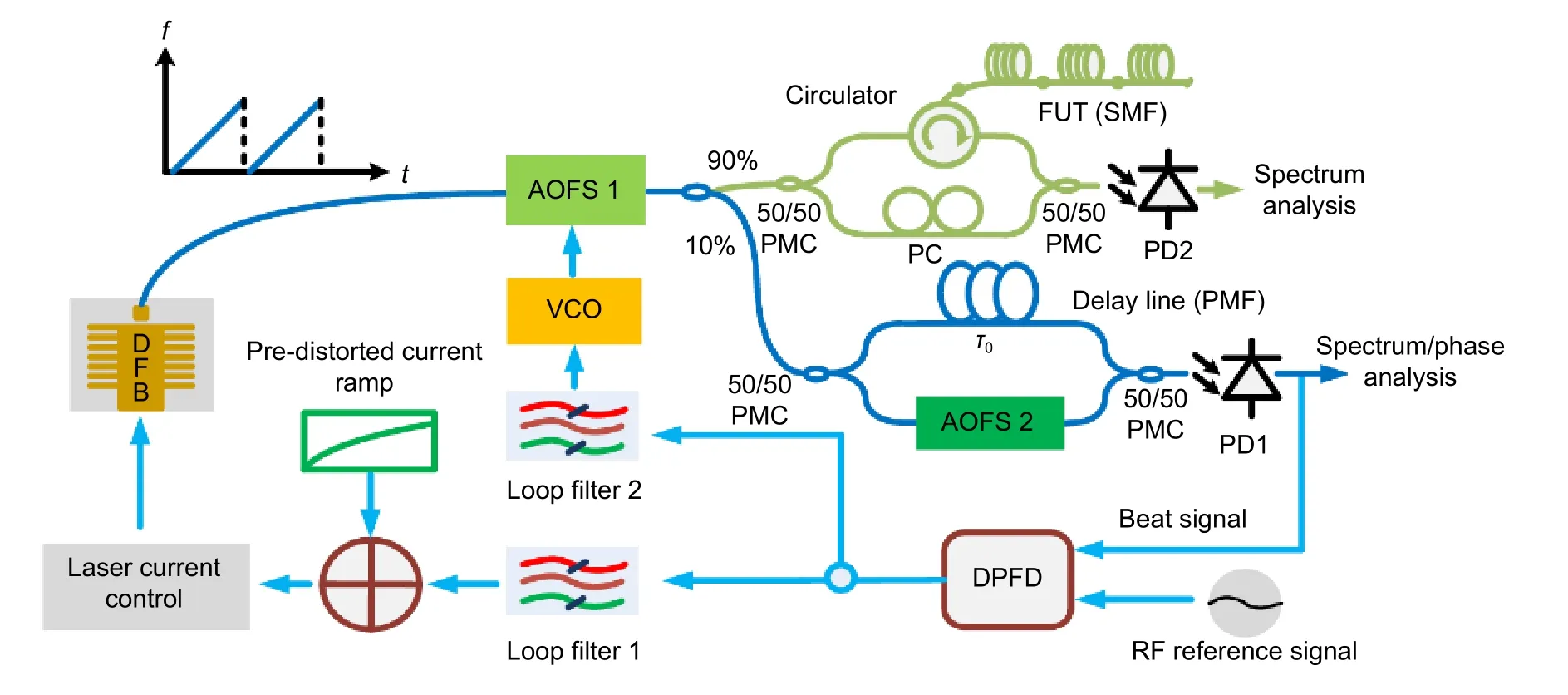
图8 实验装置示意图。AOFS：声光移频器；FUT：被测光纤；SMF：单模光纤；PMC：保偏耦合器；PC：偏振控制器；PMF：保偏光纤；PD：光电探测器；DPFD：数字相位频率检测器；VCO：压控振荡器[21]Fig.8 Schematic of the experimental setup.AOFS:acousto-optic frequency shifter;FUT:fiber under test;SMF:single-mode fiber;PMC:polarization-maintaining coupler;PC:polarization controller;PMF:polarization-maintaining fiber;PD:photo detector;DPFD:digital phase frequency detector;VCO:voltage controlled oscillator[21]

采用锁相反馈对激光源进行主动线性化控制的技术，通过改变激光器腔长及注入电流等方式来实现激光振荡参数的控制，属于激光调频中的内调制技术[24]。它能够消除大部分非线性，由于伺服系统有限的增益和带宽以及参考光纤的长度波动等，残余扫描误差总是存在[25]，但这残余误差是完全可接受的。该技术无需后续对拍频信号做非线性校正，测量准确度高；且复合光电锁相反馈回路对高度线性化、高相干性激光源的发展有积极推动作用。但是，该方法结构相对复杂，调节参数较多，对硬件要求较高，对环境要求较苛刻，容易产生失锁现象，所以其应用受到一定限制。

3.2 等光频间隔重采样

因为通过锁相反馈技术来控制激光器线性化的方法难度较大，成本较高，所以研究人员从数字信号处理部分寻求非线性校正方法。Glombitza 等人[26]在1993 年提出了用光程差已知的辅助干涉信号对测量干涉信号进行等光频采样，以此来校正激光器的频率调制非线性，获得了 50 μm 的空间测量分辨率。2001 年，Rosenfeldt 等人[27]搭建了光纤光路的等光频重采样干涉装置，并进行了光纤光栅的色散测量。等光频间隔重采样法的测量系统光路结构如图9 所示。为了便于区分，假设测量干涉光路的延迟为 τm，由于实际应用中激光器的频率调制为非线性，所以式(4)实际上应为

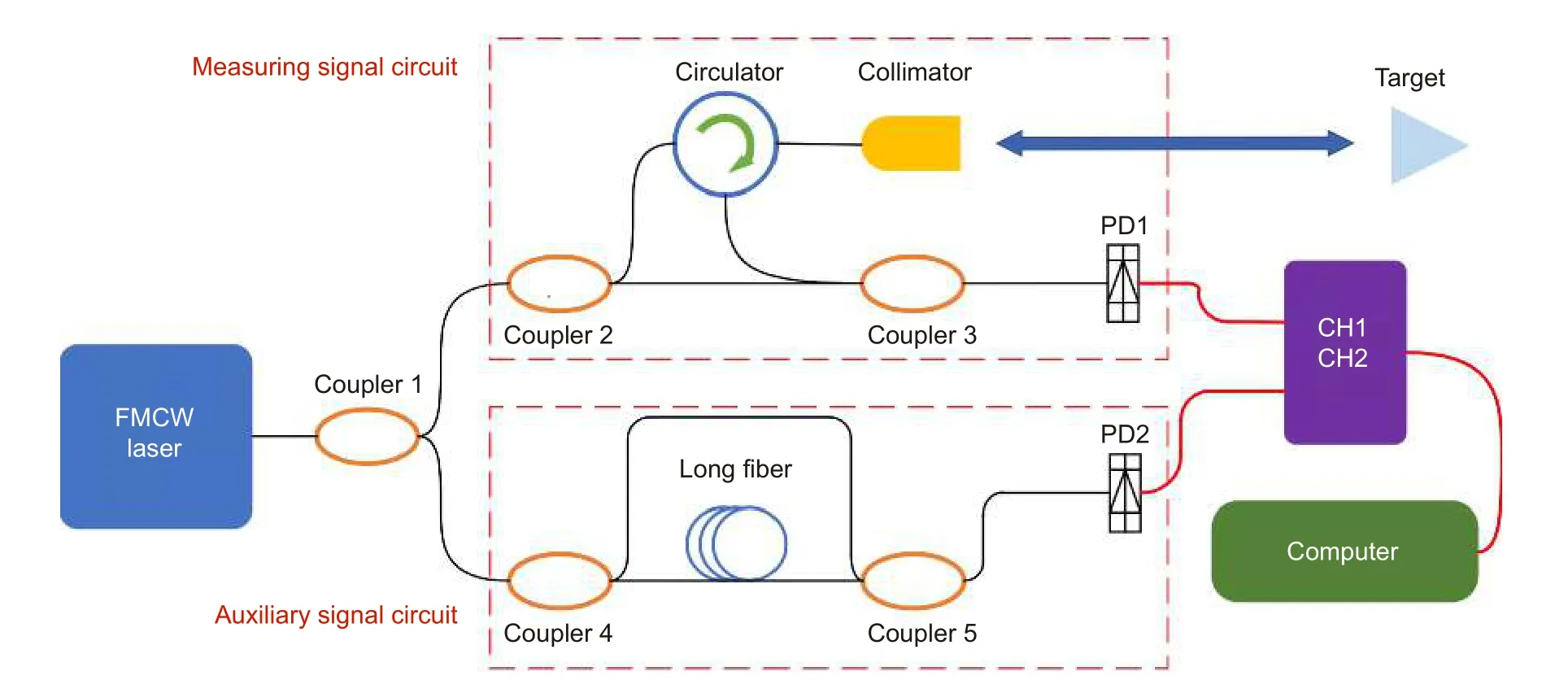
图9 等光频间隔重采样测距原理图Fig.9 Schematic of distance measurement with equal optical frequency interval resampling

同理，图9 中的辅助干涉光路产生的拍频信号经振幅归一化后，得到表达式：

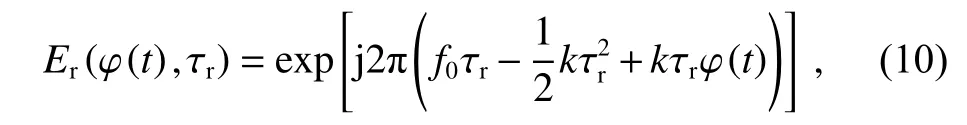
式中：τr是辅助干涉光路中光程已知的长光纤产生的延迟。

将辅助干涉光路的拍频信号作为时钟信号，提取其峰谷值点或零点作为特征点，然后对测量干涉光路的拍频信号进行重新采样，经计算可得其采样间隔为

设重采样信号的采样点数为N1，频谱图峰值点位置为K，则被测目标对应的频率为

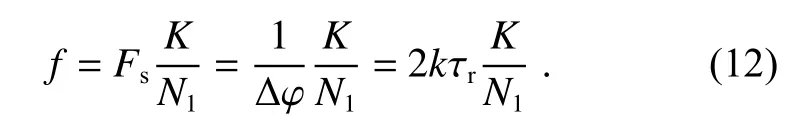
据式(12)可知，等光频间隔重采样后得到的频率为单一频率，并不受激光器调频非线性的影响。最后根据距离公式可以得到被测距离：

其中：L为辅助干涉光路长光纤的光程。值得注意的是，此方法是利用辅拍频信号对测量拍频信号进行重新采样，再考虑激光的往返，所以为了满足Nyquist采样定理，辅助光路长光纤的光程L必须大于被测距离的四倍。并且，L的标定精度会直接影响系统的测距精度。

2005 年，Ahn 等[28]提出希尔伯特变换补偿法(HTCM)，即利用辅助干涉仪的希尔伯特变换结果估计激光源的瞬时相位和频率，然后通过插值法对测量拍频信号进行等频率间隔重采样，以此抑制频率调制非线性的影响。随后，该团队又搭建了自相干装置，并用希尔伯特变换对可调谐激光器的非线性频率扫描特性进行了分析[29]。2008 年，Eric 等[30]分析了等光频间隔采样法中的干涉触发固有误差和数据采集延迟误差，给出了两种误差的解析式，并且提出在测量干涉光路中引入光纤延迟线可以有效地抵消误差，将测量信号的相位误差降低至0.2 mrad。本课题组于2012年开始了对FMCW 激光测距技术的研究。2014 年，Shi 等[31]设计了以宽调谐范围的窄线宽外腔可调谐激光器为光源的双干涉FMCW 激光测距系统，其辅助干涉仪为全光纤马赫-曾德尔干涉仪，主干涉仪是一种改进的迈克尔逊干涉仪，以减少两束光之间的干涉，如图10 所示。利用辅助干涉仪拍频信号对主干涉仪拍频信号进行等光频间隔重采样，实现了在8.7 m以内 50 μm 的空间分辨率。2017 年，Pan[32]提出了基于多信号分类(MUSIC)算法的子空间分解方法，实现高信噪比的同时，在3.814 m处距离峰的FWHM 达到了 20 μm，相比于CZT 和FFT 法分别提高了4 倍和7 倍，如图11(a) 所示；并且还引入了Cramer-Rao 下界对不同测距方法进行评定，当角锥移动285.75 mm 的相对距离时，MUSIC 算法的均方根误差仅为0.55 μm，而此时的C-R 下界为 0.18 μm，如图11(b)所示。2018 年，Shi 等[33]经过进一步研究，提出了带有两个辅助干涉仪的FMCW 激光测距系统，如图1所示。该系统增加了一个F-P 辅助干涉仪，用于实时校准M-Z 辅助干涉仪的光程差和检测激光模式跳变的时间，基本消除了扫频非线性和激光跳模对测距的影响，实验实现了在5.8 m范 围内小于± 20 μm 的误差另外，本课题组还进行了采用信号拼接提高测距分辨率[34-3、5]用自适应滤波法去除噪声的影响[35]、振动补偿方法[36]、长光纤色散补偿[37]等FMCW激光干涉测距的优化研究。2020 年，Badar 等[38]将辅助干涉仪和主干涉仪进行了集成，只需要单个信号通道就能校正扫频非线性的影响，并且还用50 m长光纤证明了所设计装置的应变和温度传感能力，该装置如图13所示。

图10 双干涉FMCW 激光测距系统示意图[31]Fig.10 Schematic diagram of the dual interferometry FMCW laser ranging system[31]

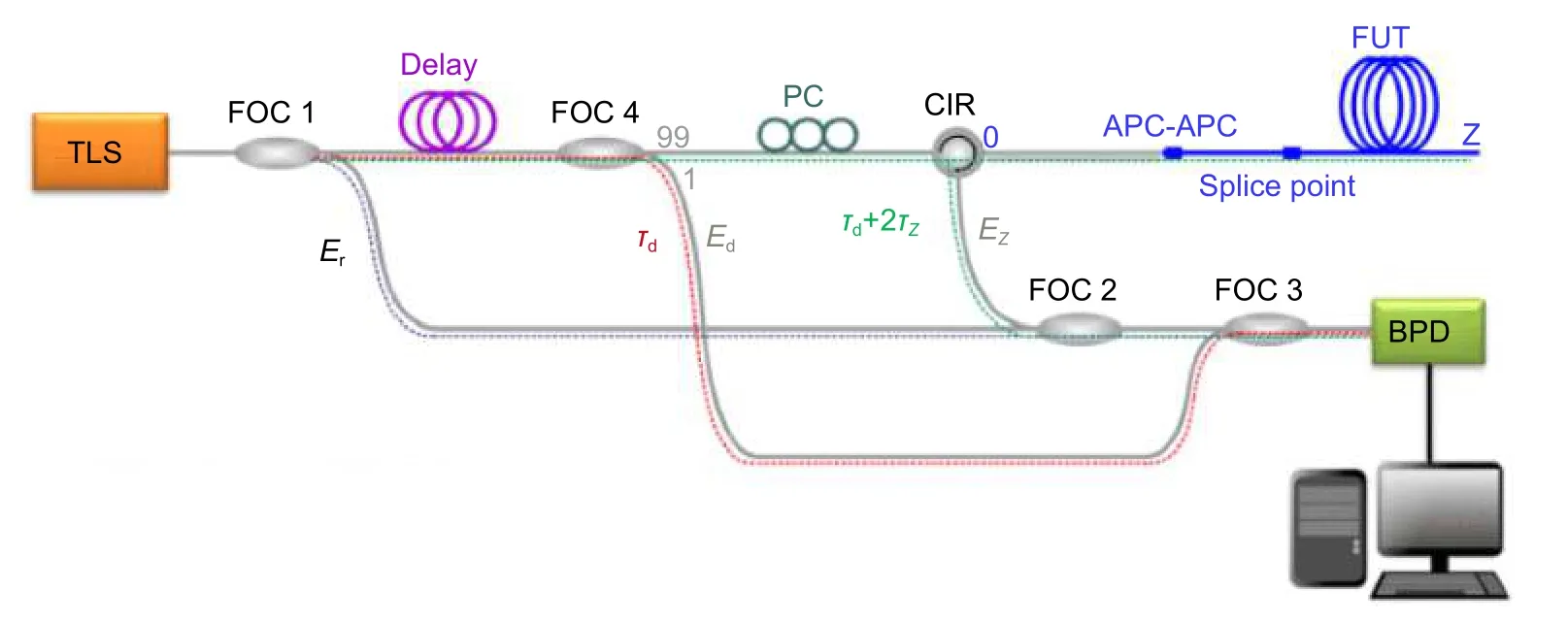
图13 一种单通道检测的调频非线性校正的新硬件结构。TLS：可调谐激光源；PC：偏振控制器；FOC：光纤耦合器；CIR：循环器；FUT：被测光纤；BPD：平衡光电探测器[38]Fig.13 A new hardware structure for correcting FM nonlinearity with only a single detection channel.TLS:tunable laser source;PC:polarization controller;FOC:fiber optic coupler;CIR:circulator;FUT:fiber under test;BPD:balanced photo detector[38]

如我们所知，经典的等光频间隔重采样法的测量范围受到辅助干涉仪光程差的限制，为了突破此限制，研究者们进行了针对性研究。2009 年，Yüksel 等[39]使用较短的延迟光纤，对测量的光学频率进行插值并确定与等距光学频率对应的时间点，然后在这些时间点对测量干涉光仪的拍频信号进行重新采样，以满足Nyquist 采样定理并消除扫频非线性误差。实验证明采用该方法能将空间分辨率提高30 倍。2019 年，Bao[40]提出等光频细分重采样法，提取辅助拍频信号峰谷值点作为特征点后，将两个特征点之间的半个周期细分为等时间间隔的N′段，再对测量拍频信号进行重采样，一定程度上减小了FMCW 测量系统的体积与成本。实验表明，在绝对距离 4.3 m范围内的测量标准差为22.23 μm。2020 年，Jiang 等[41]使辅助干涉仪信号经过用两个乘法器设计的四倍频电路板，以作为采集卡新的外部时钟信号，对6.4 m处的测量信号重新采样后解算距离，获得了 9.4 μm 的标准差。2021 年，中国计量大学的Zhang 等[7]利用希尔伯特变换对辅助干涉仪拍频信号的相位进行了扩展，实验表明，相位扩展10 倍的情况下，在约1.6 m处最大误差为19 μm。

利用辅助干涉光路进行等光频间隔重采样的方法，光学系统和电子系统的结构都比较简单，应用于在线实时测量的潜力很大，而且对信噪比要求不高，很适合于无合作目标的测量。但该方法对辅助干涉仪的光程差变化敏感，通常采用内部环境相对稳定的黑盒来放置辅助干涉仪，以保证系统的稳定性。而且在实际测量，特别是中远程测量中，测量结果受到长光纤色散等因素的影响较大，需要在解算过程中额外做出补偿。值得注意的是，等光频间隔重采样法根据重新采样方式的不同，可以分为软件插值重采样和硬件触发重采样[42-43]。两者的基本原理是一致的，但软件插值重采样是将辅助干涉仪和测量干涉仪的拍频信号分别采集，然后在计算机上利用辅助拍频信号对测量拍频信号进行重采样；而硬件触发重采样是将辅助拍频信号作为数据采集卡的外部时钟以触发对测量拍频信号的数据采集，通常是在辅助信号的零点或者对其整形后的上升沿触发采集。显然，硬件触发重采样相比于软件插值重采样，其数据采集量大大降低，节省了计算机的存储空间，提高了解算速度，更加有利于实时测量；并且能有效避免栅栏效应和峰谷值位置拟合误差，一定程度上提高了测量精度。

3.3 光频梳校正法

光学频率梳具有大带宽、窄线宽、高频率精度和出色的时序稳定性等特点，是校准线性频率调制激光源十分可靠的工具。

2011 年，美国蒙大拿州立大学的Barber 等[44]人利用光学频率梳对基于自外差光纤干涉仪锁相反馈的线性调谐激光源进行频率检测和表征。线性调谐激光源(LFC)和光频梳通过 90◦光学混合IQ 解调器混合，从而构建复信号S=I+iQ确定LFC 源和与之瞬时频率最近的梳齿的相对相位演化，以此来绘制梳齿频率(同时也是LFC 激光的频率)和时间的曲线。2013 年，Baumann 等[45]演示了一个基于光学频率梳校准的FMCW 激光雷达系统，如图14(a)所示。该系统的调频连续波激光器采用外腔二极管激光器(ECL)，且以准正弦形式扫频。ECL 激光的90%用于目标测量，10%与重复频率为200 MHz的光频梳形成外差干涉，雷达测量信号(图14(b))和ECL-Comb 外差频率被同时记录，以此得到ECL 瞬时频率(如图14(c)，经信号处理)。随后，按照等间距ECL 频率步长对记录的雷达测量信号重新采样，以此来消除频率调制非线性的影响，最后进行傅里叶变换并缩放，解算目标距离，如图14(d)和(e)所示。实现了带宽限制的130 μm 的测距分辨率和约 100 nm的测距精度。次年，Baumann 团队[46]利用FPGA 实现了基于频率梳校准激光测距系统的实时数字信号处理，将重复频率约为207 MHz的自由运行的频率梳作为时钟，数字转换器和梳齿重复频率同步采样，每0.5 ms返回一个距离测量值，每秒钟可得到2000 个测量点，并设置了一个快速转向镜(FSM)以实现二维和三维扫描，在约10 m 处获得了低于 10 μm 的标准差。图15 为该系统3D 成像的结果之一。2019 年，Yu 等[47]提出了利用窄带通滤波器标定瞬时频率的方法，如图16。扫频激光通过PBS 和锁模光梳发生外差干涉，由快速光电探测器探测并送入窄带通滤波器产生大量校准峰。利用密集的校准峰，获得多个子测量，做平均来减少距离漂移的影响，最后在约0.84 m处，得到了75 nm的标准差。同时利用子测量值表明瞬时位置的特点来监测振动，可实现振动补偿。2021 年，Xie 等[48]结合模式间距扫描频率梳和多环复合光锁相环，在校正非线性的同时，产生了具有高相干性的宽带激光。利用特别设计的电光调制器产生重复频率可调的平顶光梳，将DFB 激光器锁定到高阶模式，依赖具有大环路带宽和高环路增益的高度紧锁的复合锁相回路完成非线性校正和相干性转移。通过实验验证，相比原来的DFB 激光器，相干长度提高了约80 倍，对应的空间分辨率提高了4 个数量级。

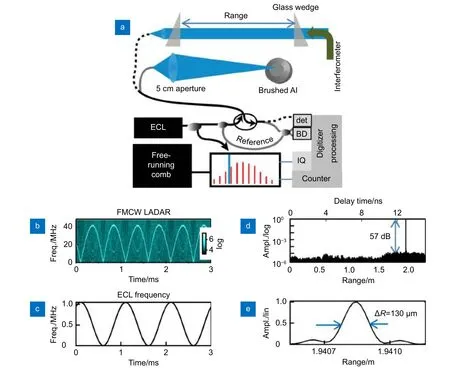
图14 (a) 实验装置。基于MEMS 的ECL 以1 ms 的周期在1 THz 上进行正弦扫描。该系统根据自由运行的频率梳测量，同时记录激光雷达外差信号和瞬时ECL 频率；(b) 测得的激光雷达信号的波形图。峰值幅度对应于fFMCW(t)；(c) ECL 瞬时频率，vECL(t)−v0；(d) 单次0.5 ms 长扫描和～10 nW～100 nW 返回功率的拉丝铝表面的距离信号；(e) 放大图说明了ΔR=0.9c/(2B)=130 μm 的未变迹、带宽受限分辨率，尽管扫描速率高达3400 THz/s[45]Fig.14 (a) Experimental setup.A MEMS-based ECL is swept sinusoidally over 1 THz with a 1 ms period.The system simultaneously records the ladar heterodyne signal and the instantaneous ECL frequency,as measured against a free-running frequency comb;(b) Sonogram of the measured ladar signal.The peak amplitude corresponds to fFMCW(t);(c) Instantaneous ECL frequency,vECL(t)−v0;(d) Range signal to the brushed Al surface for a single 0.5 ms long sweep and～10 nW～100 nW return power;(e) Expanded view illustrating the unapodized,bandwidth-limited resolution of ΔR=0.9c/(2B)=130 μm,despite the sweep rate of up to 3400 THz/s[45]

图15 (a) 一个带NIST 标志的阶梯式铝块和一个25 美分的硬币；(b) 由FMCW LiDAR 系统在z0=4.760 m 测量得到的三维假彩图；(c) 从三维图像中提取的截面(绿色轨迹)与用坐标测量机(CMM)进行测量的结果(蓝色叉线)对比图，误差(红色叉线)标准差低于 2 μm[46]Fig.15 (a) Photograph of an Al-step block with the NIST logo imprinted and a quarter located on the lower left corner;(b) False colored,3D surface image of the step block,along with a quarter on the bottom left,measured by our FMCW LADAR system at a stand-off of z0=4.760 m;(c) The FMCW LADAR image (green trace) is compared to an average of 12 measurement points taken with a CMM (blue crosses).The error (red crosses) has a standard deviation below 2 μm[46]

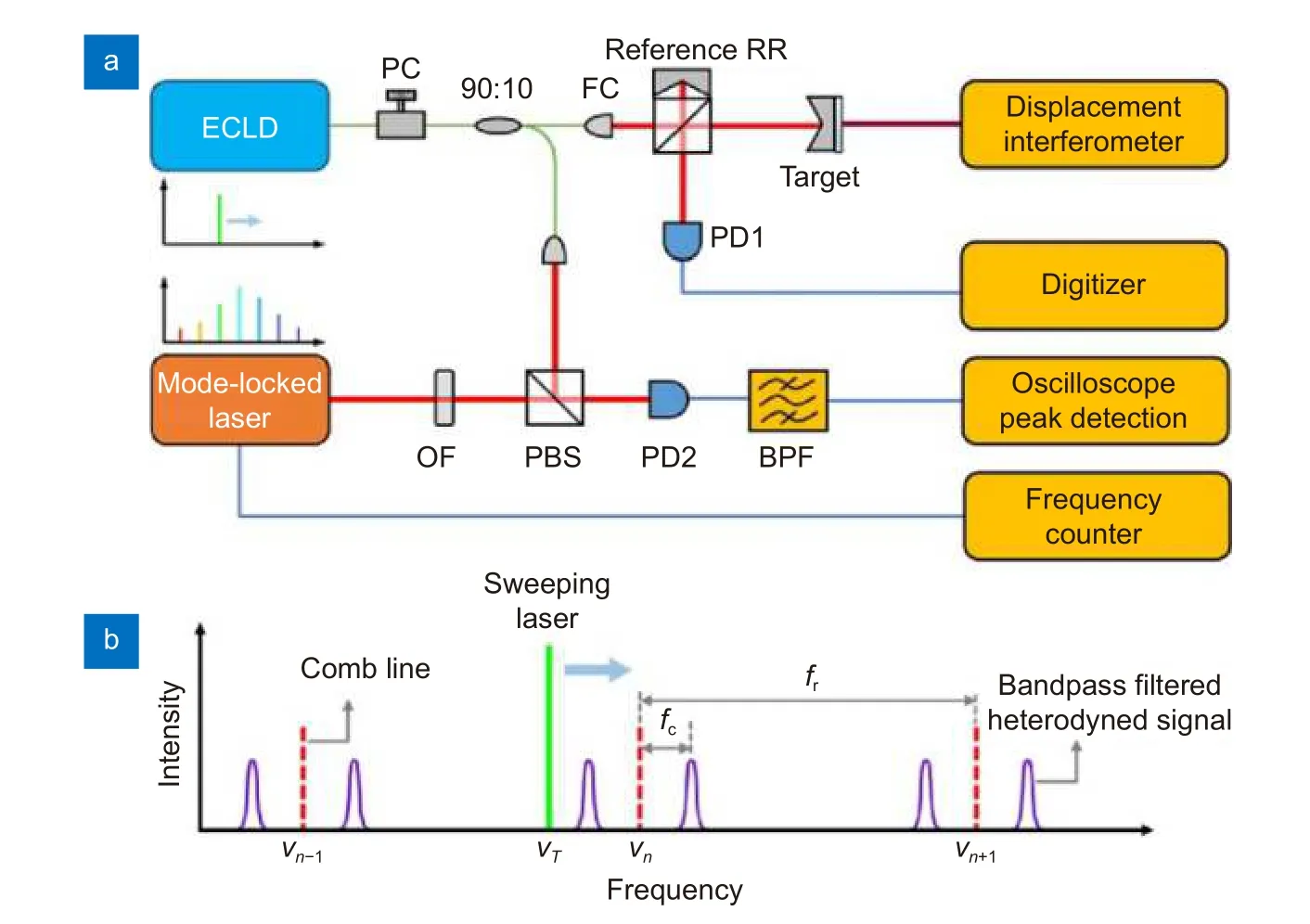
图16 (a) 利用窄带通滤波器标定瞬时频率的测量示意图；(b) 扫频激光，梳线和带通滤波器的频率位置示意图。PC：偏振控制器；FC：光纤耦合器；RR：后向反射器；PD1 和PD2：光电二极管；OF：滤光片；PBS：偏振分束器；fc：窄带通滤波器的中心频率；fr：飞秒激光器的重复率(梳状线间距)[47]Fig.16 (a) Measurement schematic diagram of instantaneous frequency calibration with narrow bandpass filter;(b) Illustration of frequency positions of the sweeping laser,comb lines,and the bandpass filter.PC:polarization controller;FC:fiber coupler;RR:retro-reflector;PD1 and PD2:photodiodes;OF:optical filter;PBS:polarized beam splitter;fc:central frequency of the narrow bandpass filter;fr:repetition rate of the femtosecond laser (comb line spacing)[47]

孤子梳是一种基于光学微谐振腔四波混频效应，器件小、光谱宽的新型光梳[49]。孤子梳的重复频率和偏移频率只与微谐振器的尺寸和材料有关，因此不需要外部参考来锁定它们。2021 年，Jia 等[15]提出了基于孤子梳的调频连续波激光雷达非线性校正法，该方法只需要采集两个信号，一定程度上减小了数据的存储和处理。图17(a)给出了所建立的系统原理图，辅助路中孤子梳和FMCW 激光雷达形成的差拍信号由平衡探测器探测，并以低采样率做欠采样，使差拍频率接近零时出现峰值，以此记录FMCW 频率接近各梳齿的时间。根据图17(b)的干涉频率和图17(c)的测距信号和校准峰可以求出测距信号的相位变化量，利用最小二乘法求出∆ φM和 ∆fFMCW曲 线的斜率k，代入公式D=k·c/4π便可求出待测距离。图18 是利用该测距系统测量约2 m处目标的信号，最终得到的测距标准差小于 11 μm，测量误差小于 μm。同年，Twayana 等[50]证明了利用自参考频率梳校准可调谐激光源的方法用于超低损耗氮化硅器件宽带光谱表征具有很大优势。在扫描波长干涉(SWI)中，可以区分高Q 值微谐振器测量中的耦合损耗和固有损耗；在光学频域反射计中，能够准确获取氮化硅螺旋波导传播损耗和群速度色散系数。

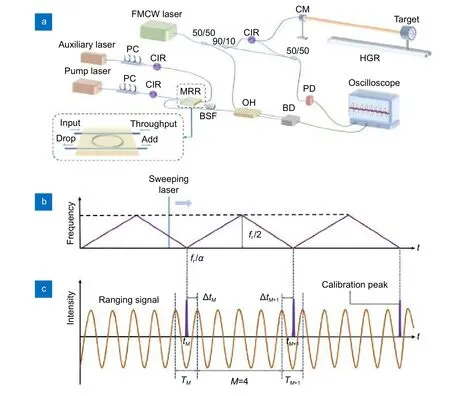
图17 (a) 实验装置示意图；(b) FMCW 激光器与孤子梳之间干涉信号的时频图；(c) 测距信号和校准峰值的时域图[15]Fig.17 (a) Schematic of the experimental setup;(b) Time-frequency graph of the interference signal between FMCW laser and soliton comb;(c) Time-domain graph of the ranging signal and calibration peak[15]

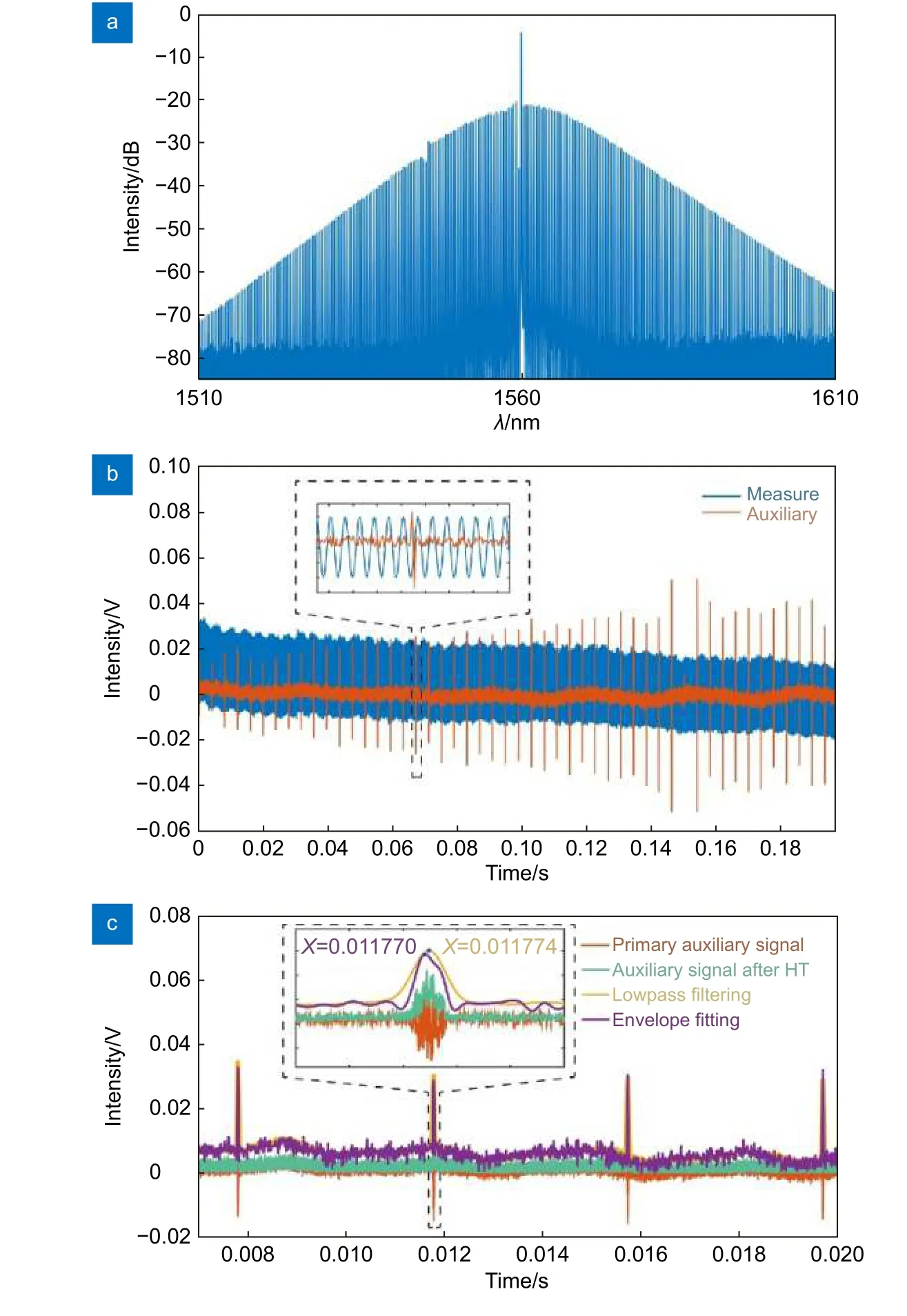
图18 (a) 滤波后孤子梳的光谱；(b) 测距信号和辅助信号的时域图；(c) 提取辅助信号中的校准峰值位置。图中包含了原始辅助信号和经过希尔伯特变换(HT)的复包络信号，以及对复包络信号进行低通滤波和包络拟合处理后的波形[15]Fig.18 (a) Spectral of the soliton comb after filtering;(b) Time-domain graph of the ranging signal and auxiliary signal;(c) Extraction of calibration peak positions in the auxiliary signal.The figure contains the original auxiliary signal and the complex envelope signal through Hilbert transform (HT),as well as the waveform processed by low-pass filtering and envelope fitting for the complex envelope signal[15]

光学频率梳可以直接将光的频率溯源到原子钟的标准，具有极高的频率精度[51]。利用频率梳来校正FMCW 激光频率调制的非线性，可实现将频率梳的频率精度向调频激光源传递，精确测量调频激光的瞬时频率来求解被测目标的距离等信息。除了高的测量精度外，采用该方法的测量系统还表现出很好的稳定性，受环境影响小，并且没有光纤色散的影响，但其系统结构相对复杂，测量成本相对较高。

3.4 相位比值法

在FMCW 激光雷达测量中，通过对含有扫频非线性的拍频信号的分析，发现其在时域上是平滑的，站在相位的角度看，其相位的变化量很容易提取出来且是一个定值，所以研究人员提出了不会受到扫频非线性影响的相位比值法。

2014 年，牛津大学的Dale 等[52]搭建了基于扫频干涉测量法的多通道绝对距离测量系统，用相位比值法解算距离被首次提出。由式(4)和式(5)可知干涉拍频信号的相位为

容易得到相位变化量∆ ϕ和 时间变化量∆t的关系为

再根据式(6)，并结合测量干涉光路和辅助干涉光路，则有：

其中：Lm和Lr分别为测量干涉仪和辅助干涉仪的光程差，∆ ϕm和 ∆ϕr分别为测量干涉仪和辅助干涉仪拍频信号在一定时间的相位变化量。

由式(16)可知，只需知道辅助干涉仪的光程差、对两个干涉仪的拍频信号进行相位提取就能得到想要的目标距离。辅助干涉仪的稳定性直接影响测量系统的精度，Dale 采用气体吸收池(H13C14N)在每次激光扫频期间都评估辅助干涉仪的光程来克服这个问题，并利用因瓦干涉仪对气体池进行了标定。该团队还引入了第二扫频激光器做反向扫频，以此来实现动态扫频干涉测量，如图19 所示，在激光功率和数据采集及处理能力允许的情况下，该系统还能实现多目标测量。实验表明，该系统能对速度为18 mm/s的线性运动目标成功测量，具体结果如图20，在 0.2 m 到 20 m范围内，其测量拟合残差和拟合相对残差如图21 所示，并且该系统运用长气体池时的相对测量不确定度达到了0.41×10−6。

图19 两个菲索干涉仪连接到两个激光器和一个气体吸收池的示意图[52]Fig.19 A diagram of two Fizeau interferometers connected to two lasers and one gas absorption cell[52]

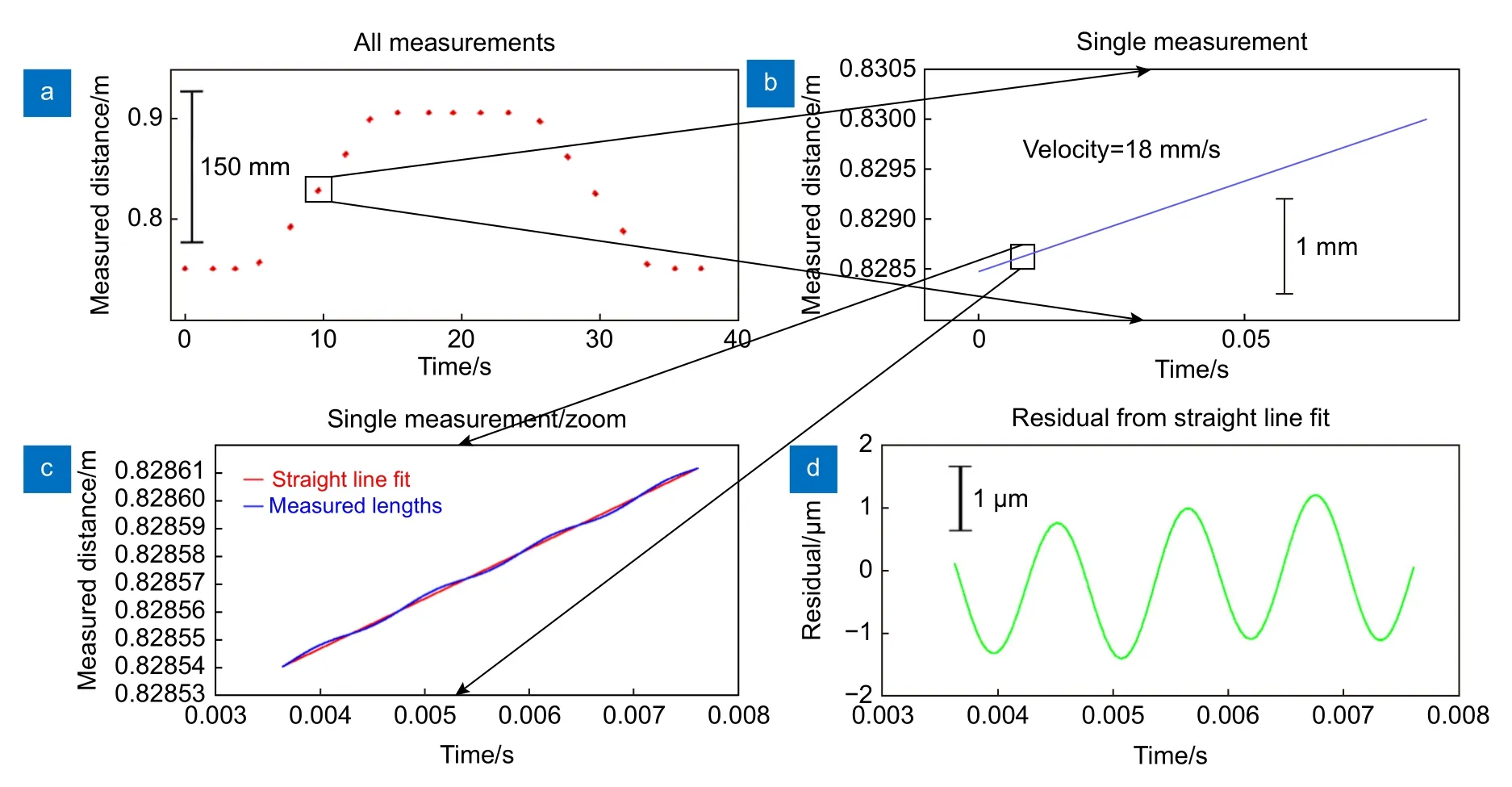
图20 (a) 测量干涉仪的多次扫描，目标在线性运动平台上；(b) 以最快的线性运动平台速度进行单次扫描；(c) 以直线拟合放大(a)；(d)，(c)拟合直线的残差[52]Fig.20 (a) Multiple scans of a measurement interferometer with the target on a linear motion stage;(b) Single scan at fastest linear motion stage speed;(c) Zoom in of (a) with a straight line fit;(d) Residual to the straight line fit in (c)[52]

图21 (a) 长距离测量数据拟合的残差；(b) 相对残差[52]Fig.21 (a) The residual of the fit to the long range test data;(b) The relative residual of the (a)[52]

进一步分析式(16)，可以看出相位提取(如希尔伯特鉴相)的精度是决定被测距离Lm精度的又一主要因素。除了采样率之外，高精度的相位提取还对拍频信号的信噪比(SNR)有较高要求。所以，相位比值法一般不适用于无合作目标的测量。

3.5 其他

近年来，除了上述较为主流的扫频非线性校正方法以外，研究人员还根据具体实验条件或应用要求提出了其他许多校正方法。这里简单总结几种供读者参考。

2012 年，日本的Fumihiko 等[53]提出了一种相位噪声补偿光频域反射测量技术(PNC-OFDR)，克服了激光器相干长度的测量范围限制。如图22 所示，对于超过相干长度的测量范围，无法再采用参考干涉仪的拍频信号对FUT 拍频信号重新采样的方法。但是，根据参考延迟 τref对测量延迟 τFUT进行分段处理再求总和的方法可以使相位噪声得到有效补偿。具体的拍频相位计算为

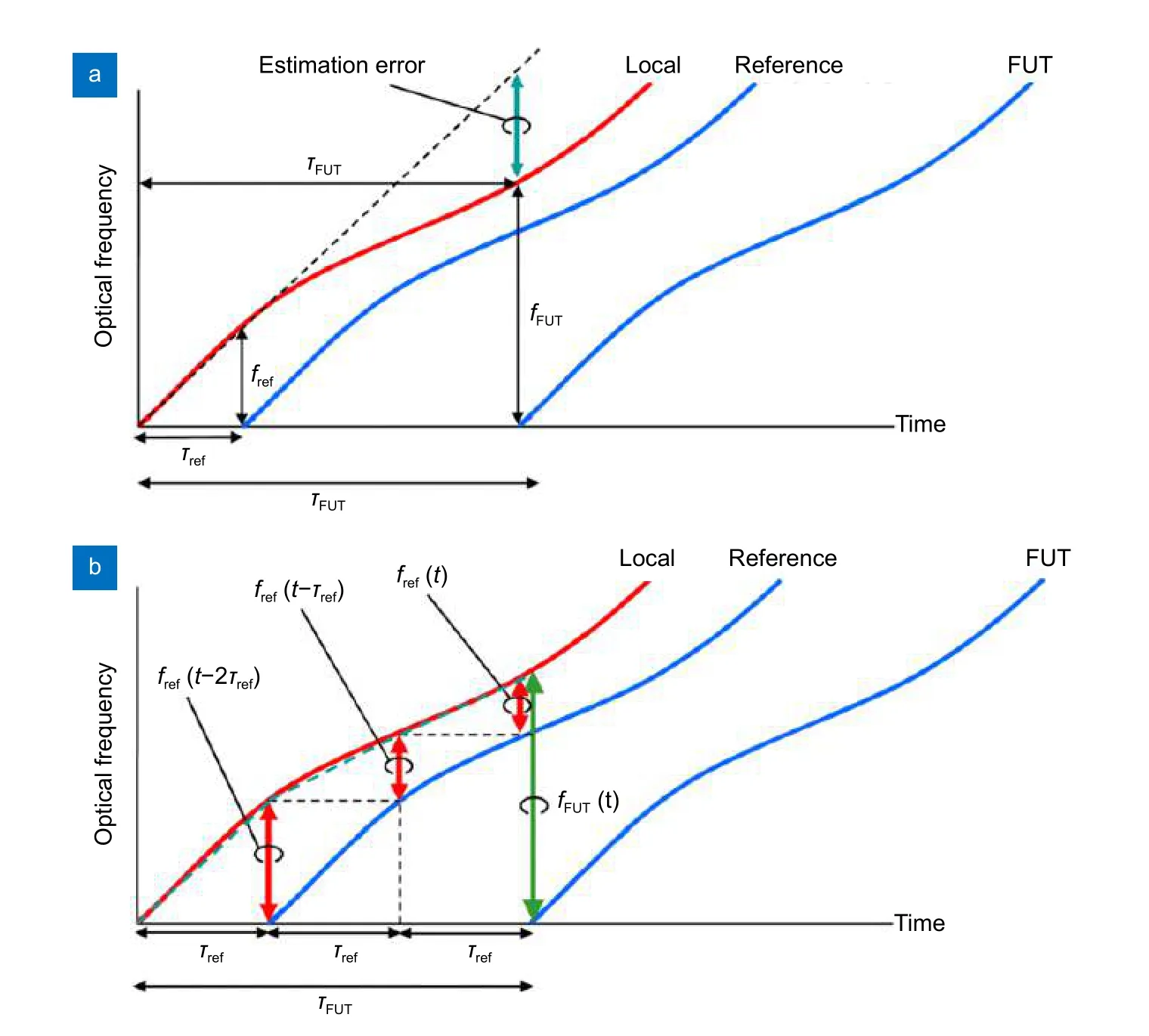
图22 PNC-OFDR 相位噪声补偿示意图[53]Fig.22 Schematic diagram of the phase noise compensation in PNC-OFDR[53]

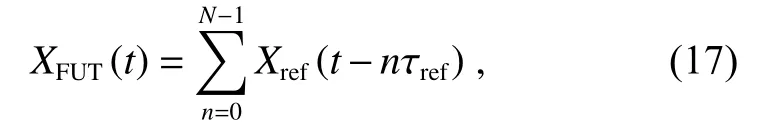
其中：N为整数，所以需要根据 τFUT=Nτref和τFUT≠Nτref的情况来分别讨论，详细内容见文献[53]。PNCOFDR 测量系统的示意图如图23，参考延迟应设置在相干长度附近，在实现全范围补偿的同时减轻计算负担。现场试验中，测量了一条长度为39.2 km的色散位移光纤，获得的3 dB分 辨率高达5 cm。

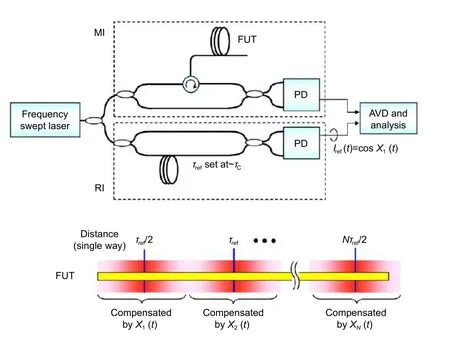
图23 PNC-OFDR 配置示意图[53]Fig.23 Schematic of PNC-OFDR configuration[53]

2015 年，Prellinger 等[54-55]利用637 nm 处碘跃迁的高分辨率饱和光谱来产生稳定的频率参考标记，从而实现扫频干涉法的绝对距离测量。在信号处理阶段，对光程差一定的辅助干涉仪的信号做相位提取，根据式(18)对测量信号在时间尺度上进行缩放重整，并通过对重整数据做样条插值来保证等间距，以此来消除激光器扫频非线性的影响。

式中：laux是辅助干涉仪光程，∆ϕaux是相位变化量，∆t是测量时间间隔，∆t′是重整后的时间间隔。

2018 年，本课题组的Zhang[56]为了消除等光频间隔触发重采样系统中测量干涉仪和辅助干涉仪响应时间和传输时间差异的影响，提出了一种基于幅度调制的FMCW 测距法。其原理如图24(a)所示，将辅助干涉光路与测量干涉光路用一个2 ×2的耦合器串联，激光先进入辅助干涉仪生成载波信号，而后通过测量干涉仪对载波信号进行幅度调制，调制后的信号由数据采集卡获取。实验采集到的混频信号如图24(b)所示，通过提取混频信号的极大值点得到幅值信号，这相当于对测量拍频信号做了一次等光频间隔重新采样。经推导，激光的扫频非线性对带有距离信息的幅值信号没有影响，所以能准确解算出目标的距离。

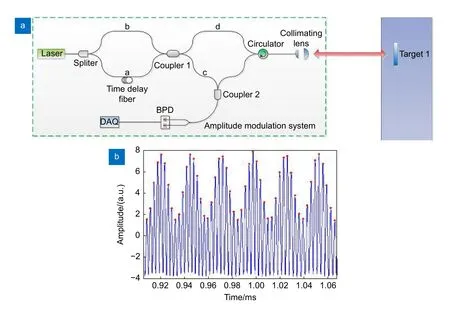
图24 (a) 基于幅度调制的FMCW 测距系统示意图；(b) 调幅系统的混频信号[56]Fig.24 (a) Schematic diagram of FMCW ranging system based on amplitude modulation;(b) The mixing signal of the amplitude modulation system[56]

研究人员还利用算法来抑制或消除扫频非线性的影响[57-58]。2019 年，Zhang 等[58]为了更加简单直接地抑制激光器的扫频非线性，提出了一种基于迭代学习控制(ILC)预失真的激光扫频线性化方法。其控制示意图如图25(a)，vd(t)为 期望的激光扫频，uk(t)和vk(t)为第k次迭代时更新的电压波形和激光频率，将频率误差ek(t)带 入电压更新算法uk+1(t)=uk(t)+p·ek(t)得到下一次的驱动电压，直到得到最终的预失真激光驱动电压波形ud(t)。图25(b)是一个常规的激光扫频测量装置。将ILC 预失真算法应用于商用VCSEL，设置49 GHz的扫频带宽，得到的扫频结果如图26 所示，可见扫频线性化效果明显。

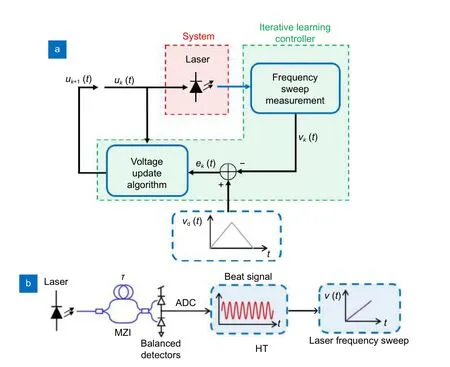
图25 激光扫频线性化的ILC 预失真示意图。(a) ILC 过程的框图；(b) 激光扫频测量的详细设置[58]Fig.25 Schematic of ILC pre-distortion of laser frequency sweep linearization.(a) Block diagram of the ILC process;(b) Detailed setup for laser frequency sweep measurement[58]

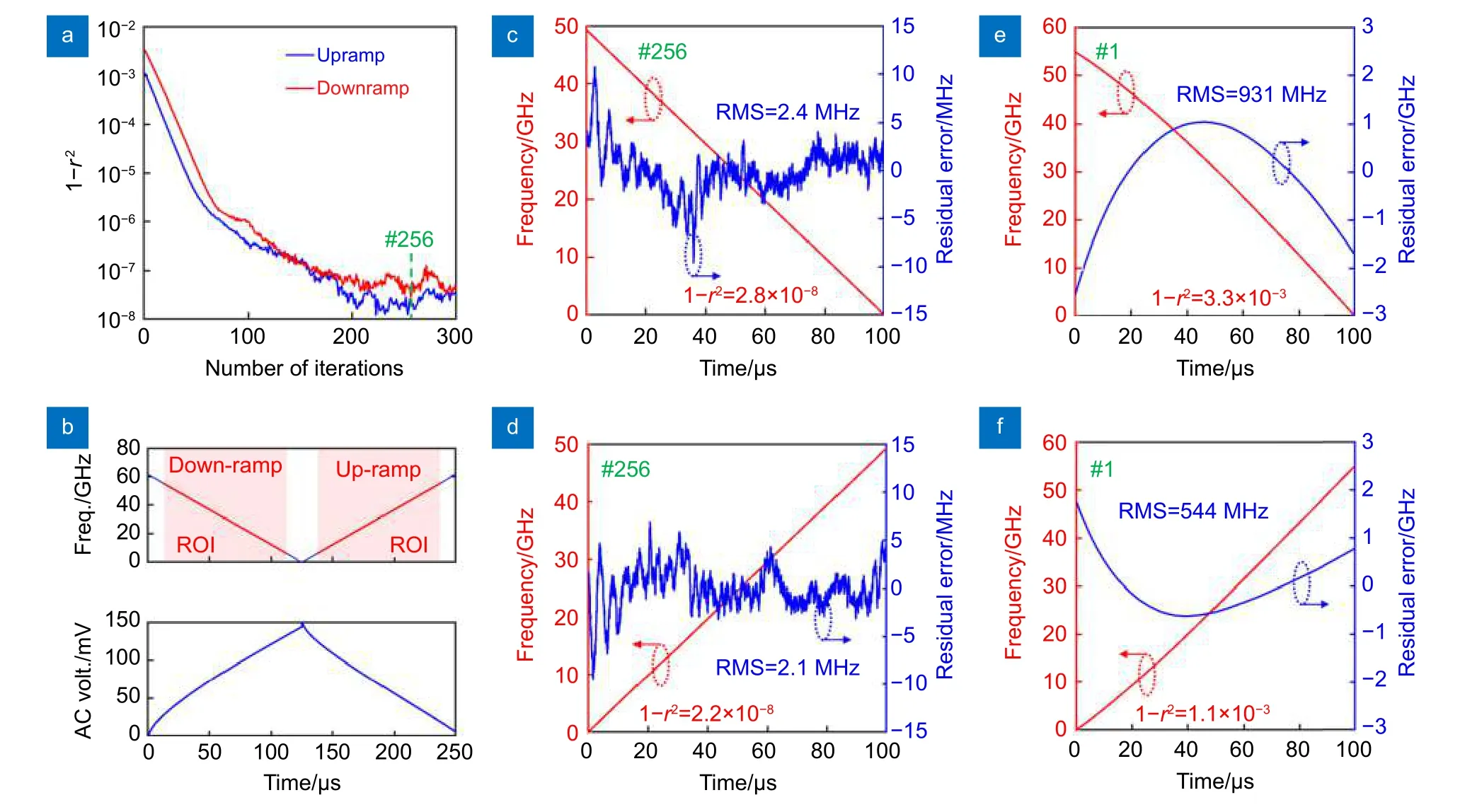
图26 ILC 对VCSEL 激光扫频线性化的实验结果。(a) 残余非线性与迭代次数的关系；(b) 第256 次迭代的激光频率扫描和相应的驱动电压波形。ROI 用红色标记；(c)，(d) 第256 次迭代的ROI 中的向下和向上斜坡激光频率扫描和残余误差；(e)，(f) 用于比较的第一次迭代的向下和向上斜坡激光频率扫描和剩余误差[58]Fig.26 Experimental results of laser frequency sweep linearization of VCSEL by ILC.(a) Residual nonlinearity versus the number of iterations;(b) Laser frequency sweep and the corresponding drive voltage waveforms at the 256th iteration.The ROI is labeled by red color;(c),(d) The down-and up-ramp laser frequency sweeps and residual errors in the ROIs of the 256th iteration;(e),(f) The down-and up-ramp laser frequency sweeps and residual errors of the 1st iteration for comparison[58]

2021 年，Dong 等[59]结合了边带调制和注入锁定技术实现了带宽为 6 GHz 的线性扫频和 dB 的大载波抑制比。其系统示意图如图27(a)，将主激光器出射激光通过MZM 调制产生的±1 阶边带注入到DFB二极管激光器中，驱动MZM 的RF 信号的频率从8 GHz 到14 GHz 线性啁啾，并将DFB 从激光器的中心频率固定在−1 阶边带的中心频率上，完成注入锁定。主激光器经调制后的光谱(红色)，从激光器光谱(黑色)和注入锁定后的光谱(蓝色)如图27(b)所示。通过边带调制和注入锁定技术，主激光器的窄线宽特性和AWG 信号源的线性调频特性被引入到从激光器，产生了相干长度大、扫频线性度高的FMCW 测量系统。经过距离测量、速度测量以及三维成像等实验，证明了该方法效果显著。

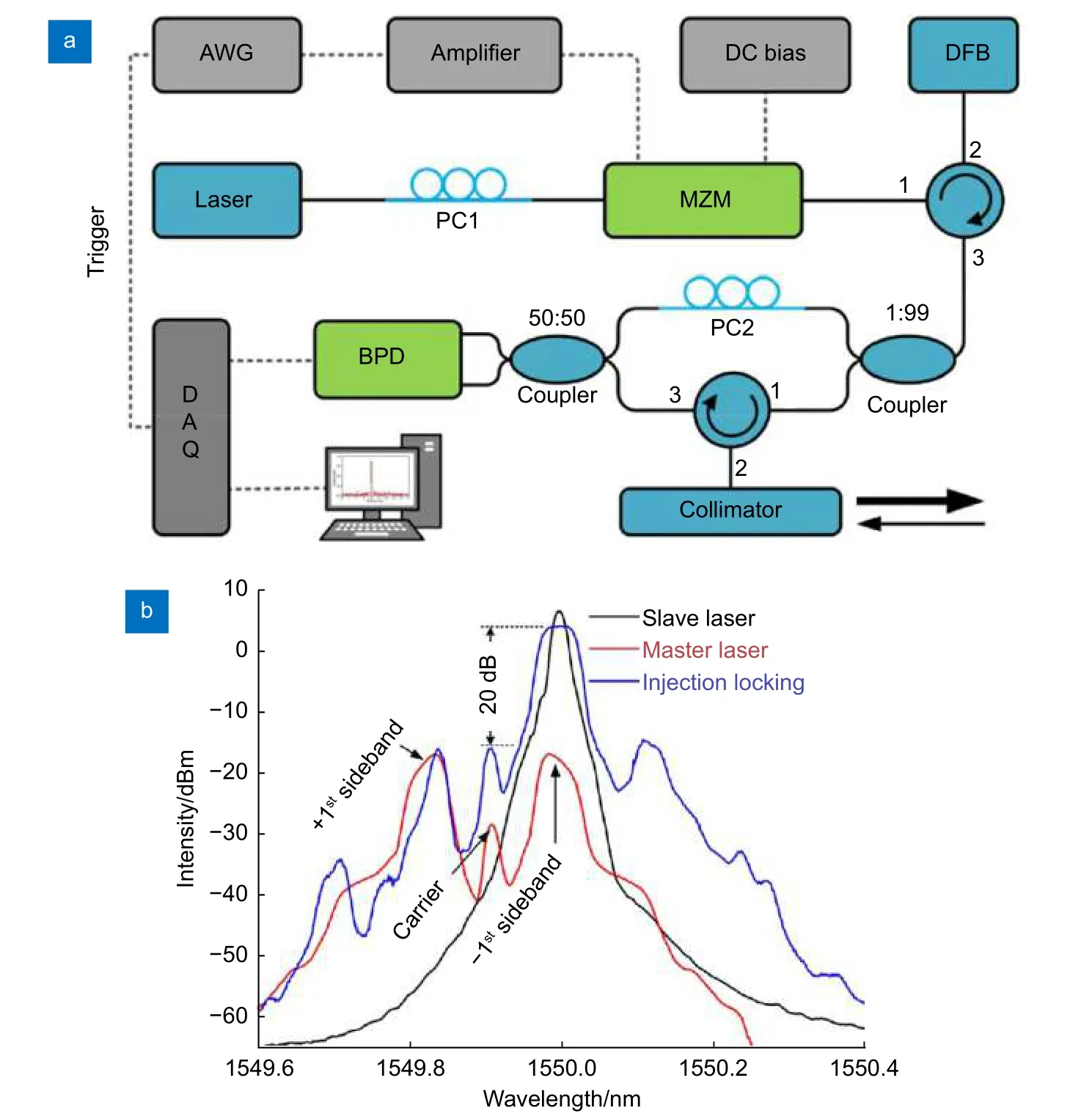
图27 (a) 基于FMCW 的LiDAR 系统的示意图。AWG：任意波形发生器；DFB：分布式反馈激光器；PC：偏振控制器；MZM：Mach-Zehnder 调制器；BPD：平衡光电探测器；DAQ：数据采集卡。实线表示光路，虚线表示电子路；(b) 光调制后的主激光器(红色)、没有光注入的从激光器(黑色)和注入锁定后的从激光器(蓝色)的光谱[59]Fig.27 (a) The sketch diagram of the proposed FMCW-based LiDAR system.AWG:arbitrary waveform generator;DFB:distributed feedback laser;PC:polarization controller;MZM:Mach-Zehnder modulator;BPD:balanced photodetector;DAQ:data acquisition card.Solid line means light path and dash line means electronic path;(b) The optical spectra of the master laser after optical modulation (red),the slave laser without the optical injection (black),and the slave laser after the injection-locked (blue)[59]

随着硅光子学的发展，采用片上集成电光调制器来输出高线性度激光光源的方式成为一大热点[6,60-61]。Aflatouni 等[61]在2015 年报道的一种集成硅纳米光子相干成像仪(NCI)，就是以频率啁啾电压u(t)驱动Mach-Zehnder 调制器对激光进行强度调制，利用电信号产生的线性频率啁啾避免了对具有高度线性可调谐激光源的需要，并演示了在0.5 m范 围内具有 15 μm深度分辨率和50 μm 横向分辨率的三维成像。2021 年，Nicolaescu 等[6]采用焦平面阵列方式实现了片上集成的远距离兼高深度精度的大规模像素3D 成像。其高线性度的FMCW 激光源是由硅光子IQ 调制器调制一个1550 nm 的单频激光产生，该系统架构如图28 所示。该系统仅使用 4 mW 的光，在75 m的距离达到了3.1 mm的精度，其远距离成像效果如图29。采用片上调制器获取高线性度啁啾光源对单片集成FMCW LiDAR 的发展意义重大，但是其调谐带宽受到限制，一般只能达到几GHz 或是几十GHz，这限制了测量系统分辨率的进一步提高。

图28 固态三维成像系统架构[6]Fig.28 Solid-state 3D imaging architecture[6]

图29 (a) 54 m 处堆叠的纸箱和其点云图；(b) 75 m 处外墙和其点云图。与目标的距离用(a)和(b)中的颜色表示[6]Fig.29 (a) Point clouds of stacked cardboard boxes at 54 m;(b) Point clouds of exterior wall at 75 m.Distance to the target is indicated by color in (a) and (b)[6]

4 总结与展望

在现代科学技术迅猛发展的今天，大型装备制造、智能驾驶、生物医疗和国防等领域对精密测量技术提出了更高的要求。不管是微距和短程，还是中远程和超远程测量，都需要对测量手段的准确度、稳定性、测量效率和便捷程度等方面进行综合考虑。FMCW激光雷达测量技术有着极高的测量分辨率和测量灵敏度，且无需接触和合作目标，在现代精密测量技术中展现出了较大潜力。

频率调制非线性校正是FMCW 激光雷达测量技术研究中的重要问题。本文在讲述FMCW 激光雷达测量原理的基础上，根据校正原理的不同，介绍并分析了各种激光频率调制非线性校正方法。通过表1 对文中介绍的几种校正技术的重要参数和实验结果进行对比。实验数据表明：基于锁相反馈控制的激光频率主动线性化技术的测量重复性精度很高，测量标准差小于 100 nm。这得益于内调制技术获得的大调谐范围和锁相反馈带来的较高的补偿精度。此外，它能够明显减轻后续数字信号处理的负担，但由于要对激光器的注入电流和压电驱动器等进行控制，所以对硬件要求较高且结构相对复杂，并且扫描速度过高或外界环境恶劣时容易发生失锁。利用光学频率梳的非线性校正方法也展现出较高的精度，并且在几千太赫兹每秒的高速扫描下也十分稳定。通过与频率梳进行干涉，将频率梳可溯源到原子钟的标准的高频率精度传递给了FMCW 激光雷达，使测量精度得到有效提高，微谐振腔孤子梳的出现也让测量设备的集成化方向更加明朗。等光频间隔重采样法在实际测量中的精度相较前两者略低，因为该方法受辅助延迟光纤的光程抖动和光纤色散影响较大，且在信号处理过程中提取特征点时，无法保证严格的等间隔，不过其系统结构设计较为简单，对信噪比要求也较低。运用相位比值法的测量精度也相对略低，它在系统结构上与等光频间隔重采样法相近，在算法上利用测量干涉仪和辅助干涉仪的相位变化量与光程差成比例的特性来解算结果，所以对辅助延迟光纤也具有很大依赖，且该方法受到鉴相精度的直接影响，对信号的信噪比要求较高。由前文可知，等光频间隔重采样法和相位比值法都需要搭建辅助干涉仪，且通常需要对辅助延迟光纤的长度做实时监测来保证测量精度。因此，在条件允许的情况下，建议可直接采用气体(CO 或H13C14N)吸收池进行距离测量。即把等光频间隔重采样光路结构中的辅助干涉仪换成气体吸收池光路，同时采集测量拍频信号和气体吸收光谱，如图30 所示；将测量拍频信号的相位看作是光频率的函数，通过最小二乘法拟合相位与光频率的直线，求解直线斜率，便可得到测量延时 τm，从而得到目标距离。这样既不受调频非线性的影响，也无需标定辅助延时长光纤，更不用考虑长光纤带来的色散失配问题，但是此法对噪声比较敏感。

图30 基于HCN 气体吸收池的FMCW 激光雷达测距系统Fig.30 FMCW LiDAR ranging system based on HCN gas cell

表1 四种FMCW 激光雷达测量的非线性校正技术重要参数和实验结果对比Table 1 Comparison of parameters and experimental results of nonlinear correction techniques for FMCW LiDAR

除上述方法外，研究者们还提出了许多校正频率调制非线性的方法，如基于迭代算法、注入锁定技术或是电光调制器的校正方法，它们都有着各自的优势。可以看到，现在主要的非线性校正方法都是从光学测量系统和数字信号处理算法入手，但我们更希望能够从源头上解决问题，即从激光器本身的设计入手，对其机械结构、电路设计、温度控制等做出进一步改进，即要努力实现较为理想的线性频率调制光源。当然，在实际的测量应用中，除了非线性校正问题外，我们还需要考虑色散补偿[62-67]、振动补偿[68-72]等环境因素补偿。

目前，FMCW 激光雷达测量技术已经发展得较为成熟，逐步走出了实验室，已有可靠的商用产品推出并应用于工业现场，如Nikon 的MV350，HEXAGON 的Absolute Multiline Technology 等。但是这些设备的体积都较大，不够便携，使其应用场景受到限制。区别于传统的单点测量，为了提高FMCW 激光雷达的成像帧率，基于孤子微梳的大规模并行相干激光雷达测量系统被提出[73]，这为自动驾驶等领域提供了新的思路。在全球智能化发展的浪潮下，FMCW 激光雷达测量技术等精密测量的相关设备也必将向集成化、低成本、低功耗、高度实时化等方向稳步迈进。在过去十多年里，多路复用单元、调制器、放大器和光电探测器[74-75]等部件已经能够实现硅上的混合集成或异构集成[76]，对于难度较大的隔离器和循环器等器件，可通过磁光(MO)材料和硅光子学结合[75]的方式实现集成。而对于硅光子学关键器件的片上激光器，虽然宽调谐环形谐振腔半导体激光器[77]和高功率窄线宽激光器[78]也已经被报道，但仍需要进一步研究。综合来看，上述光器件集成的商业化实现主要体现在光通信和生物传感领域[79]，而激光雷达测量领域的片上集成相关报道中，大多是利用电光调制器[6,60-61]或是锁相环反馈[20,80-82]来获取高线性度的啁啾光源进行测量，另外微谐振腔光学频率梳[83]和光学相控阵(OPA)扫描[84-87]也较为热点。有了这些技术作基奠，相信不久后，FMCW激光雷达测量系统的光子集成电路和自由空间光的接口会得到很大推动，集成芯片上能够集成更多复杂的光学材料和器件，乃至实现真正的单片高精度FMCW 激光雷达测量系统，这一旦取得成功，必然会有效促进精密测量等各相关领域的发展。