细长刚体块系统中的混沌现象及其Lyapunov指数谱计算
蒋金凯,杜正东
(四川大学数学学院,成都 610064)
1 引 言
在非光滑动力系统中有多种多样的分岔现象.近年来,随着非光滑动力系统在工程应用领域得到越来越多的应用[1,2],对其动力学行为的研究也日益深入[3].其中,由不连续诱导分岔产生的非光滑动力系统的混沌现象是微分方程与动力系统研究的一个热点.另一方面,原本应用于光滑动力系统的Lyapunov指数谱计算方法也被推广应用在各种非光滑动力系统中[4,5].Lyapunov指数谱度量了系统相邻轨道的平均收敛程度,可以作为一种判定系统混沌的指标.
细长刚体块模型是一个典型的分段光滑系统,在研究地震对刚体结构的影响等方面有诸多应用.研究表明[6-8],该模型的动力学行为非常丰富,不仅可以通过鞍结点分岔、音叉分岔、倍周期分岔等产生各种碰撞周期轨道,进而导致混沌,还可能通过异宿分岔产生混沌.本文首先将文献[4]中的Lyapunov指数谱计算方法推广应用于类似细长刚体块的其它非光滑动力系统,然后通过数值模拟验证:当外部周期激励的振幅改变时,系统可以通过异宿分岔产生混沌,最后利用Lyapunov指数谱验证了这种混沌现象.
我们首先引入以下概念.
定义2.1当动力系统的轨道反复穿越同一截面时,在连续运动的轨道上用一个截面(称Poincaré截面)将其横截,利用轨道在截面上穿过的情况就可以判断运动的状态.记S为Poincaré截面,xn(n=0,1,2,…)为轨道前一次穿过S的点,xn+1为轨道后一次穿过S的点,那么,xn+1可看成xn的映射:
xn+1=f(xn),n=0,1,2,...,
称为Poincaré映射.
显然,由上述映射f可定义一个离散动力系统.
定义2.2对上述的离散动力系统,考虑一个起点在x0处的无限小位移矢量y0,其在映射f下演变过程可用以下方程表示:
yn+1=Df(xn)·yn,n=0,1,2,...,
其中Df表示映射f的Jacobi矩阵.|yn|/|y0|描述了无限小位移的增减比率.因此,系统在满足初始条件x0及沿初始方向u0=y0/|y0|的Lyapunov指数定义为
Lyapunov指数描述了相空间相邻轨道的平均指数发散率的数值特征.若映射f是n维的,则存在n个Lyapunov指数,分别对应于n个线性无关的初始方向.将这n个数值按从大到小的顺序排列起来,所得结果称为离散动力系统的Lyapunov指数谱.
图1为细长刚体块系统的力学模型.假设该刚体块是质地均匀的,其重心与几何中心R重合.同时,在施加外部水平激励时,若不考虑滑动和弹跳现象,则该刚体块在激励作用下反复绕两个底角A,B转动.在每次变换转动角时,刚体块与地面发生碰撞.当α≪1时,其无量纲运动方程由以下常微分方程[6]表示:

图1 细长刚体块模型
(1)
其中,x表示刚体块的角位移,k表示系统的阻尼系数,β,ω分别表示外部水平激励的振幅和频率.当x=0时,碰撞发生,tA,tB分别表示发生碰撞的前后时刻.由于是刚性碰撞,因此tA=tB.r表示碰撞的能量恢复系数.进一步,我们将系统(1)改写为如下自治系统:
y(tA)=ry(tB),x=0
(2)
由于碰撞的存在,系统轨道在经过碰撞面时不连续,这导致系统的向量场在该处的Jacobi矩阵不存在.因此,光滑系统中利用Jacobi矩阵计算Lyapunov指数谱的方法便不再适用.为了解决这一问题,我们采用类似文献[4]中的方法,结合局部碰撞映射构造Poincaré映射,将非光滑系统转化为离散动力系统,进而采用离散动力系统计算Lyapunov指数谱的方法.为了达到这一目的,我们首先介绍如何构建系统(2)的Poincaré映射及计算该映射的Jacobi矩阵.
3.1 Poincaré映射的建立
为了叙述方便,我们首先给出以下子空间的记号:
y>0,φ=φa},
y<0,φ=φb},
Σ+={(x,y,φ)∈R2×S1|x=0,y>0}=
{(y,φ)∈R×S1|y>0},
Σ-={(x,y,φ)∈R2×S1|x=0,y<0}=
{(y,φ)∈R×S1|y<0}.

(3)

(4)
(5)
上式中I为3维单位矩阵,·和*分别表示向量的内积和2阶张量.
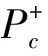
(i)从定相位面到碰撞面的局部子映射
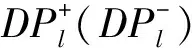
(ii)从碰撞面到碰撞面的局部子映射
利用系统中的碰撞关系式,可得到局部映射P2(P5)的Jacobi矩阵为
(iii)从碰撞面到定相位面的局部子映射

由上述三类局部映射构成的复合映射为
上述映射的Jacobi矩阵可通过链式求导法则分别求得
下面接着定义系统(2)在两个非碰撞阶段的子映射,分别记为
因此,由式(3)定义的Poincaré映射P可以表示为以上映射的复合,即
(6)
由复合映射的求导法则,Poincaré映射P的Jacobi矩阵可写成
(7)
3.2 Lyapunov指数谱的计算方法
根据式(3)(7)定义的Poincaré映射P及其Jacobi矩阵,令
(8)
则离散动力系统Lyapunov指数谱通常定义为[6]
(9)

在直接利用(9)式计算Lyapunov指数谱的过程中,由于要求迭代的次数N→∞,经常出现病态问题,导致M中的元素或者变得很大(对于混沌吸引子),或者变为0(对于周期吸引子),使得计算结果与实际情况不符.为了消除该问题,常采用QR分解将矩阵MN转化为正交矩阵QN和上三角矩阵RN,文献[4]中给出了其具体的计算过程.因此,Lyapunov指数谱的计算式转化为
(10)

在得到系统的Lyapunov指数谱后,我们可以根据其特征判定系统此时的状态.其中,周期解的所有Lyapunov指数都为负,拟周期解至少存在一个Lyapunov指数为0,且其余的Lyapunov指数都为负,而混沌解至少存在一个Lyapunov指数为正.
4 数值模拟
对细长刚体块系统的研究可追溯到上世纪九十年代.Hogan在文献[6]中研究了该系统可能存在的(1,n)型稳定周期轨道的参数范围,其中(m,n)型周期轨道表示该周期轨道在一个周期内经历了2m次碰撞,且其周期是外部激励周期的n倍,并解析的给出了其发生鞍结点分岔与倍周期分岔的条件.进一步,Hogan还计算了系统的异宿轨的扰动稳定流形与扰动不稳定流形的解析形式,利用Melnikov方法得到了系统发生异宿分岔的临界参数条件为[7]
(11)
其中,
并推测系统在满足参数条件β>βM时可能会产生混沌,但没有通过数值模拟进行验证.下面我们选取满足β>βM的适当参数,通过相应的数值模拟来观察系统是否会产生混沌.
选取系统固定参数k=1,ω=5,r=0.925.此时βM≈12.4702.当β=15时,选取初始迭代点为(10-8,0),去除前10 000个暂态点的影响后,系统存在稳定的对称(1,1)型周期轨道,如图2所示.其中,实线表示系统的碰撞面,虚线表示此时系统的稳态轨道.图3展示了该吸引子的Lyapunov指数谱序列的收敛情况.从该图中可见,序列的收敛速度和收敛性都很好,且系统在该参数条件下的两个Lyapunov指数(分别以实线和虚线表示)的收敛值都小于0,其中最大Lyapunov指数λ1≈-0.039,表明系统此时处于周期运动状态,与数值模拟结果相符.
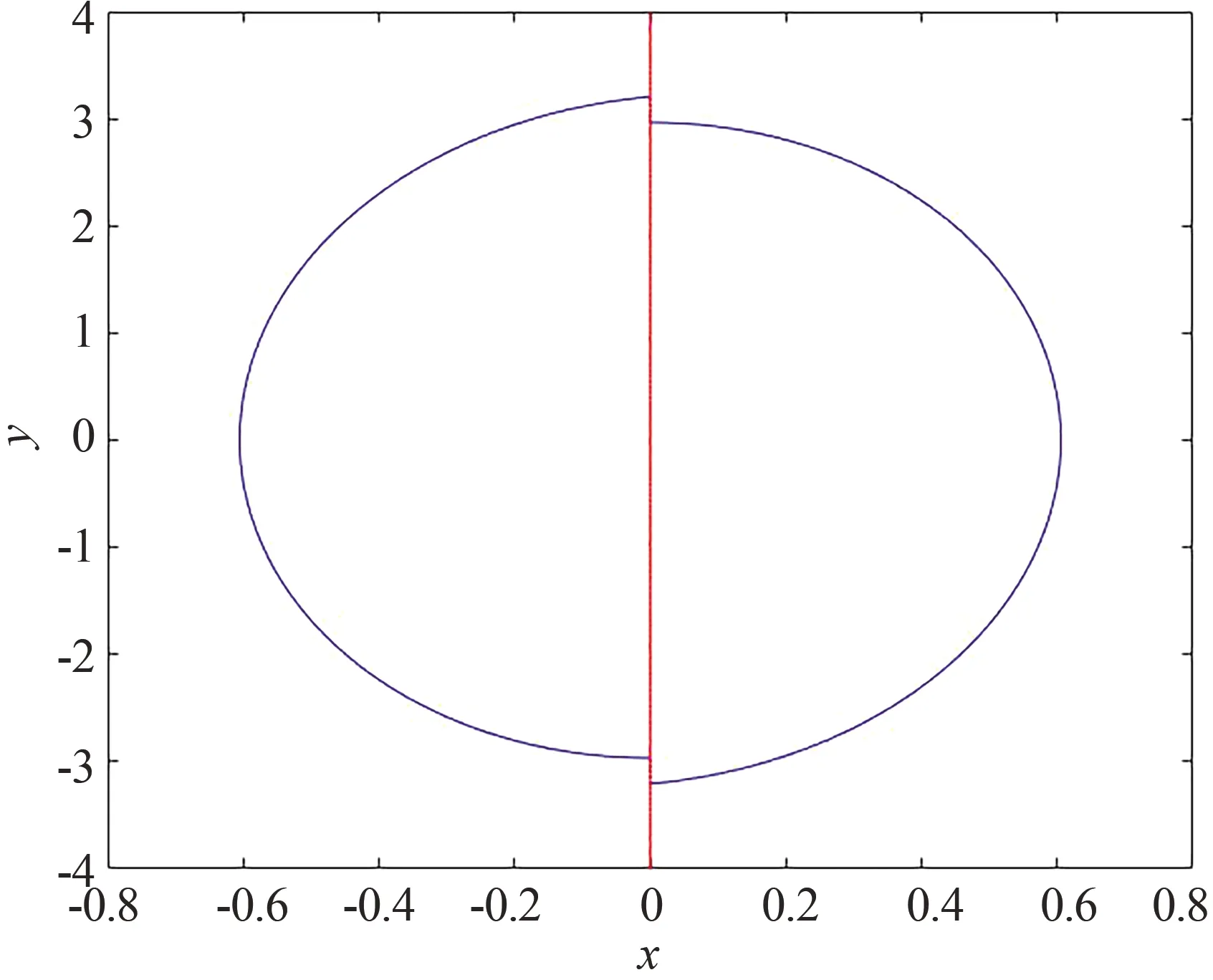
图2 (1,1)型周期吸引子相平面图
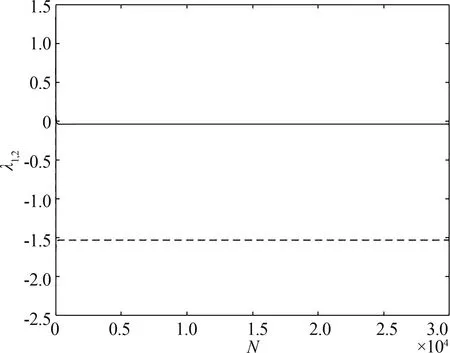
图3 周期吸引子Lyapunov指数谱收敛序列
当β=23.6时,去除暂态点影响后,系统吸引子的相平面图如图4所示.为了进一步确认系统是否处于混沌状态,图5展示了该吸引子的Lyapunov指数谱序列的收敛情况.如图所示,系统在该参数条件下具有一个正的Lyapunov指数λ1≈0.260,由此可说明系统此时正处于混沌状态.

图4 混沌吸引子相平面图

图5 混沌吸引子Lyapunov指数谱收敛序列
通过以上的数值模拟,我们验证了系统发生异宿分岔后的确会导致混沌.
5 结 论
通过对细长刚体块系统进行数值模拟,我们证实了文献[7]中关于异宿分岔会导致混沌的猜测.值得注意的是,这可能只是该系统产生混沌的必要条件,因为在相同的参数条件下,当改变系统初始迭代点时,其产生的稳态现象可能不同.此外,我们推广了文献[4]中一类碰撞振动系统利用Poincaré映射计算Lyapunov指数谱的方法.与文献[4]不同的是,本文所研究的刚体块系统在碰撞面两端的向量场是不同且不连续的,而这导致了碰撞阶段子映射的Jacobi矩阵计算上的差异,且构建的Poincaré映射P中包含了两次碰撞过程.虽然在计算上略显繁杂,但由于碰撞的特性相同,因而可将该方法推广至具有多个碰撞面的Filippov系统.同时,本文利用Lyapunov指数谱验证了刚体块系统发生的混沌现象.数值模拟结果与Lyapunov指数计算结果的相容性也证明了我们推广的Lyapunov指数计算方法的正确性和有效性.

