基于负载均衡的大规模TTE消息调度表生成方法
叶 帆,陈银超,王 涛,季袁冬,罗懋康,3,江秀强
(1.四川大学空天科学与工程学院, 成都 610207;2.航空工业成都飞机设计研究所,成都 610073;3.四川大学数学学院,成都 610064)
1 引 言
分布式航电系统在航空航天领域具有广阔的应用前景[1,2].此类系统要求机载网络必须具备高实时性、高容错性、高确定性及高带宽等特性.时间触发以太网(Time-Triggered Ethernet, TTE)被认为是未来机载网络的理想解决方案[2,3].时间触发以太网基于全局同步的时钟协议实现高确定性、高实时性的时间触发通信,并根据离线确定的静态通信调度表来传输时间触发消息.当前,针对TTE调度表生成方法虽然已有较多的研究,但尚未形成统一标准,仍需深入研究[4,5].
针对机载网络的大规模数据调度需求,本文研究TTE消息的路径规划和调度方法.文献[6-9]设计了基于不同规则的静态优先级调度方法.这些方法大多采用TTE现有的AS6802标准[2]给出的星型、雪花型拓扑,消息路径唯一,且使用最短路径策略生成消息路径,规则确定、复杂度低,对大规模消息调度问题可行性好、计算时间也少,但是,这些方法没有考虑到多径及端系统规模超过50个[8]的复杂拓扑等情形,在实际应用中容易出现因最短路径上的负载过大而造成消息阻塞的问题,无法进行后续的时序调度.
负载均衡在路径规划和时序规划问题中的应用越来越多[10-13].文献[10]构建了一个考虑负载的路径代价函数,利用深度优先搜索算法寻找最小代价值的路由.文献[11]基于K最短路径(K shortest paths, KSP)算法计算各业务的备选路径,在保证待选路径的较优性的前提下利用遗传算法优选出尽可能使全网负载均衡的业务路径组合.文献[12]则研究了时间触发(Time-Triggered, TT)流量路径规划和时序规划对速率受限(Rate Constrained, RC)流量实时性的影响,并根据KSP算法和链路最大负载最小的原则进行路径规划.但是,就我们所知,能够服务于大规模数据传输需求和负载均衡要求的机载网络的高效数据调度方法还未出现,有待进一步研究.
针对复杂拓扑条件下机载网络的大规模数据高效传输问题,本文提出了一种基于负载均衡思想的TTE消息调度表生成方法.该方法主要有以下几个特点:
(i)考虑了复杂网络拓扑.与星型网络及雪花型网络等相比,本方法中的消息路径并不唯一;
(ii)考虑了消息长度的影响.相比单个时隙传输,本方法具有更好的实时性;
(iii)设计了基于负载均衡和静态优先级的调度分配方法.
此外,本方法具有较低的算法复杂度,适用于对大规模消息数据进行高效地时序规划.
2.1 TTE消息传输
TTE支持三种类型的流量在网络中传输,即TT流量, RC流量和尽力而为(Best-Effort, BE)流量[2-6].针对机载网络的实际需求,本文仅考虑TT流量的传输.TT流量根据各网络节点所加载的静态调度表中预定义的时间进行传输,由全局同步时间触发,具有确定的延迟和抖动.该流量常被用于具有严格确定性和实时性要求的情形,能够满足未来机载网络对大规模数据传输确定性和时效性的需求.
时间触发以太网在空间和时间维度上调度网络流量,使得网络具有确定性,即确定数据包何时在何链路上传输,以及何时最终到达其目的端口.这种调度在空间维度上体现为路径规划,需要为每个数据包找到一条合适的路由,即由链路和交换机组成的网络路径;在时间维度上是时序规划,需要沿着每个数据包路由的链路分配时隙(slot),每个时隙仅保留用于所配置帧的传输.具体的传输过程如图1所示.
路径规划需要确定消息传输所经过的网络节点.在图1中,Sender为发送端,Switch为交换机,Receiver为接收端.此外,还有两条消息,其中浅灰色的TT消息周期为2ms, 从Sender1传输到Receiver,传输路径为
Sender1→Switch1→Switch3→Receiver,
深灰色的TT消息周期为3ms,从Sender2传输到Receiver,传输路径为
Sender2→Switch2→Switch3→Receiver.
消息在数据流链路上传输过程中的时序规划就是确定消息间的先后顺序.在图1中,两个TT消息(深灰色和浅灰色所示)同时在Switch3到Receiver的链路上传输,消息间的先后关系以它们的集群周期为基准.因为浅灰色TT消息和深灰色TT消息的周期分别为3 ms和2 ms,其集群周期,即消息周期的最小公倍数(least common multiple, LCM)为6 ms.因此,可以根据消息传输的开始时刻与集群周期的开始时刻间的时间间隔的长短来衡量消息的先后.

图1 TT消息传输示意图
2.2 TTE消息调度模型
与传统的星型及雪花型网络拓扑不同,实际的机载网络规模大、拓扑结构复杂.为了验证大规模、非单一路径网络拓扑下的算法性能,本文以TTE多跳网络拓扑[13]为基础,将三组多跳网络拓扑互联组合形成如图2所示的TTE多跳互联网络.该网络中有终端系统(End System, ES)及网络交换机(Network Switch, NS)这两种节点角色,各节点之间通过全双工链路进行连接.在图2中,ES与NS之间的双向箭头代表矩形中各ES与NS之间均存在全双工链路,只不过为了表示清晰在此简化为一条双向箭头.在各个节点中,算法将加载离线生成调度表.根据调度表中的派发时刻和接收时刻, 算法对TT消息进行传输,转发行为只允许发生在网络交换机中,全双工链路允许双向通信.

图2 TTE多跳互联网络拓扑
将网络模型建模为有向图G=[V,L],其中V为网络节点集合,V=ES∪NS,L为网络中数据流链路的集合.数据流链路是两个节点间的定向通信连接,lpk=[vp,vk]∈L,vp,vk∈V.
定义网络拓扑矩阵G,
(1)
其中,存在vi,vj∈V,使得当数据流链路lij存在时网络拓扑矩阵元素Gij值为1,当数据流链路lij不存在时网络拓扑矩阵元素Gij值为0.
定义集群周期为消息周期的最小公倍数.由于TT消息均为周期性消息,调度过程随LCM呈现周期性重复.因此,本文所讨论的调度表生成问题只考虑一个LCM内的消息调度即可.
TT消息帧格式符合ARINC 664p7规范,消息通过帧的有效载荷进行传输.本文假设所有TT消息为周期性消息,且不考虑打包和分段.将TT消息建模为如下的6元组形式,通过该6元组能够完整描述TT消息的传输行为:
mi={mi.period,mi.length,mi.source,mi.dest,
mi.path,mi.offset}
(2)
其中mi.period表示消息周期对应的时间长度,mi.length表示消息长度引发的传输时间对应的时间长度,mi.source表示消息传输源节点,mi.dest表示消息传输目的节点,mi.path表示消息传输路径,为数据流链路的有序序列,mi.offset表示消息相对集群周期起始时间的偏移量.为了将时序规划问题简化为整数规划问题,我们使用时隙[5]作为调度表的时间单位对消息的周期和消息传输时间进行整数化处理,使得mi.period为消息周期对应的时隙数,mi.length为消息长度引发的传输时间对应的时隙数.
本文主要考虑如何以确定性的优化规则分配大规模消息数据的传输路径和传输时隙.为了研究方便,并结合实际应用[2-6],我们作如下的假设:
(i)网络中所有消息都为周期性的TT消息;
(ii)网络中所有链路资源都可用,交换机采用存储转发方式;
(iii)只考虑TT消息单播的情形;
(iv)调度表设计时以时隙为单位对消息周期、消息传输时间进行化整;
(v)假设网络中每次发送的TT消息都能封装在一个帧里,且一个帧只传输一条消息,不考虑帧的打包和分段.
3 基于负载均衡的调度表生成方法
网络消息的路径规划过程根据消息的源节点mi.source,目的节点mi.dest和网络拓扑G确定各个消息的传输路径mi.path.该路径为数据流链路的有序序列{l1,l2,…,ln},具体实现过程如图3所示.首先,我们使用Yen’s KSP算法[14]生成各个消息的待选路径集合,然后根据规则对消息进行排序,最后按照排序顺序依次为消息从待选路径集合中选择网络链路最小负载最小的路径,加入规划路径集合.

图3 路径规划流程图
3.1.1 负载计算公式 定义数据流链路lkp上的负载B的计算公式为
(3)
其中,mi.path为消息传输路径,mi.period为消息周期对应的时隙个数,mi.length为消息长度引发的传输时间对应的时隙个数.网络最小链路利用率Bmin为
(4)
其中k,p为网络节点vk,vp.
3.1.2 排序规则 生成待选路径后,为了选出负载均衡的路径结果,我们首先需要根据规则对消息进行排序.本文考虑消息长度带来的影响,定义规则为消息长度越长,排序越靠前,优先进行路径选择;消息长度越短越靠后,在已选路径的负载基础上进行路径选择,相同长度的消息按照原本顺序进行排序.
3.1.3 选择过程 为了达到负载均衡的目的,本文选择使得消息路径中链路最小负载最小的路径作为路径规划的结果.由于某些消息的传输任务路径唯一,导致一些主干链路的负载很高且难以缓解,因而设计链路最小负载作为路径选择的条件能够关注到较小负载的均衡状况,以达到负载均衡的目的.
3.2 时序规划方法
针对大规模消息的调度问题,本文设计了一种静态优先级调度方法.与智能优化算法相比,该方法的计算时间更少、效率更高.此外,该方法基于规则,因而具有确定性.对于已知传输路径的消息时序规划问题,调度过程需要确定各个消息在其路径的各个数据流链路中的首个数据帧的偏移量offsetij(第i个消息在路径第j个数据流链路上传输时首个消息帧偏移量),同时还要确定该消息帧传输的结束时刻endij,具体过程为:首先根据优先级评估计算公式计算消息优先级,然后按照从小到大的顺序对消息进行优先级排序,评估值越小时排序越靠前、优先级越高,最后根据优先级排序依次按照规则对消息进行调度分配.
(i)优先级评估值计算.由于优先级较高的消息将先进行时序规划,较低优先级消息的排序会受到已规划消息的影响,因而应使得较难调度的消息先进行时序规划,较易调度的消息靠后.鉴于单调速率算法[15]已证明,根据消息周期进行优先级排序具有最优性,消息周期越短,本文综合考虑消息周期与消息长度对优先级排序的影响,消息周期越短,优先级越高,消息长度越长,优先级越高;反之,消息周期越长,消息长度越长,优先级越低.优先级评估值pi的计算公式为
(5)
这样,优先级评估值pi越小,消息周期越短、长度越长,优先级越高.当消息优先级评估值相同时,按消息原始顺序进行排序.
(ii)调度规则.优先级排序后,我们将按照优先级顺序对消息进行调度.若该消息为链路中首个被调度的消息,则令其集群周期偏移为0,该链路中后续消息将与前一个消息“背靠背”排布进行调度.若产生冲突,则令该消息后移一个slot,直到无冲突.若无法消除该冲突,则无法生成调度表.具体规则如(6)~(8)式所示.
endi,j=offseti,j+mi,length
(6)
(7)
(8)
其中offseti,j表示消息i在其路径中第j个数据流链路上的传输时刻距离集群周期LCM起始的偏移量,cont(mi.pathj)表示数据流链路mi.pathj上已规划的消息偏移个数,endi,j表示消息i在其路径中第j个数据流链路上传输完毕时刻距离集群周期LCM起始的偏移量,delayi,j表示消息i在其路径中第j个数据流链路上传输的硬件延迟和排队抖动,该数据依据实际的网络物理性能而离线设定.
4 仿真与分析
4.1 仿真设置
路径和时序规划仿真实验的硬件配置CPU为Intel(R)Core(TM)i7-10510U、内存16GB,采用MATLAB R2016a进行编程计算,并利用PyCharm Community Edition 2021.1.1 x64开发平台进行SMT对比仿真.
仿真采用的网络拓扑如图2所示,包含55个端系统和6个交换机,共61个网络节点,且转发行为只发生在交换机上.在仿真程序中,该网络拓扑表示为矩阵G61×61的形式,如式(1)所示,矩阵元素Gij为1时节点i到节点j间存在数据流链路lij,矩阵元素为0则表示不存在数据流链路.
由文献[11],我们设置网络链路的传输速率为100 MB/s,并根据TTE帧格式(符合ARINC 664p7)设置帧长为64~1518 B.由文献[2],我们设置消息周期为15、25、30、50、75、150 ms,时隙长度为0.5 ms,并据此对消息周期和帧长进行取整计算,可得帧长传输时隙为1~3 slot,消息周期时隙为30、50、60、100、150、300 slot.在可达的前提下,令消息端口均匀分布,消息传输需求示例如表1所示.
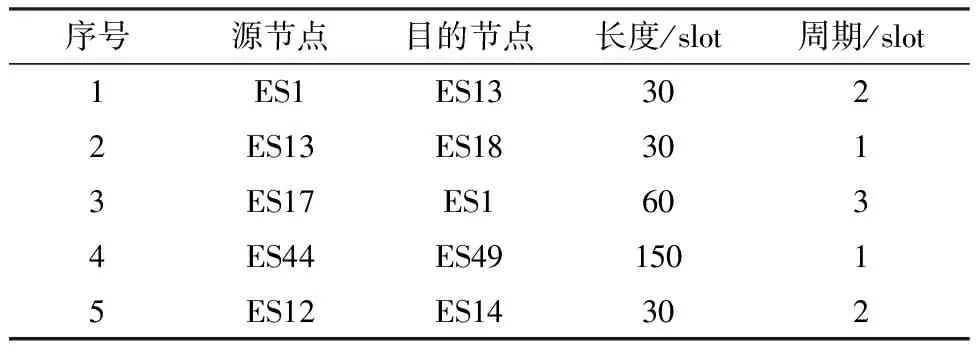
表1 消息传输需求
为了验证本文所提方法的有效性和在时间复杂度方面的性能提升,我们采用传统的迪杰斯特拉(Dijkstra,DIJ)路径规划算法[6,16]和经典的基于满足性模理论(Satisfiability Modulo Theory, SMT)的时序规划方法[5],并与本文所设计的基于K短路径的负载均衡路径规划方法及基于规则的静态优先级调度(Static Priority Scheduling, SPS)方法综合,得到四种方法组合,并在不同消息规模下进行对比仿真实验.这四种方法分别为:DIJ最短路径算法+SMT时序规划方法(DIJ+SMT),基于K短路径的负载均衡路径规划方法+SMT时序规划方法(KSP+SMT),DIJ最短路径算法+基于规则的静态优先级调度方法(DIJ+SPS),以及基于K短路径的负载均衡路径规划方法+基于规则的静态优先级调度方法(KSP+SPS).对四个方法组合在不同消息规模下进行仿真实验时的具体消息设置参见表2.

表2 仿真实验消息设置
4.2 仿真结果与分析
4.2.1 仿真结果 我们以表2中第二组消息为例展示本文方法仿真结果,DIJ算法与KSP方法的路径规划结果分别如图4a和4b所示,两种方法的时序规划结果如图5,6所示.图4展示了部分路径结果矩阵Path100×5,其中矩阵行元素为调度消息序号,列元素为路径结果中数据流链路排列序号,矩阵中的元素代表了传输路径中数据流链路的序号,0代表无链路即无路径.
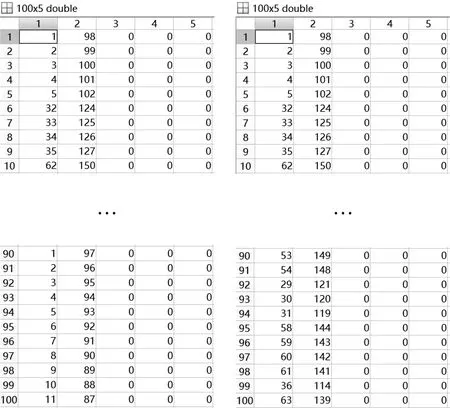
图4 路径规划结果:(a)DIJ算法路径矩阵;(b)KSP方法路径矩阵
可以看出,当消息为1~10时,两种路径方法结果相同.这验证了KSP方法的有效性和正确性.当消息为90~100时,KSP方法的数据流链路路径与DIJ算法不同.我们以第90个消息为例进行分析.DIJ算法的路径结果为数据流链路1传输至数据流链路97,KSP算法的路径结果为数据流链路53传输至数据流链路149.由于两个算法第1个消息的路径结果均为数据流链路1传输至数据流链路98,因而对于第90条消息而言,KSP算法缓解了数据流链路1上的负载.由此,我们可以推断其他消息的链路负载情况,尤其当网络中链路负载不均匀时,DIJ算法中最短路径的负载难以缓解,更容易出现路径阻塞的现象.
图5和6展示了TT消息调度表,表的横坐标以时隙为单位,表示一个LCM内的消息帧排布情况,纵坐标表示网络中的数据流链路序号,图中的黑色小矩形代表各消息已被分配的时隙,通过调度表能够确定消息在网络中传输的路径和时间顺序.

图5 KSP+SMT时序规划结果
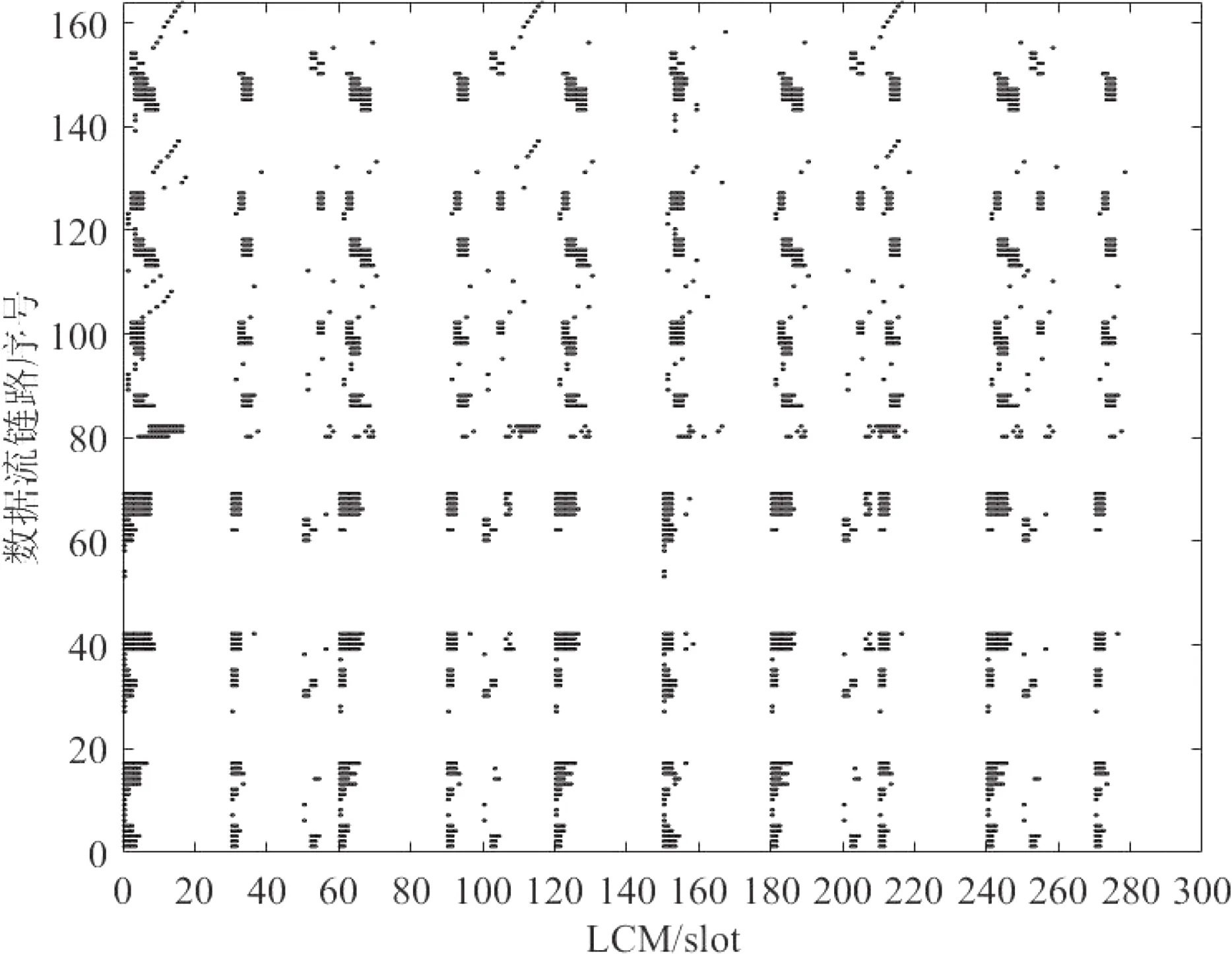
图6 KSP+SPS时序规划结果
由于消息路径中数据流链路上的时隙偏移offset决定了调度表中消息被分配的时隙的位置,因而通过图7和8中的时隙偏移offset分布直方图和分布曲线图可以看出,本文设计的SPS方法因采用了“背靠背”的排布规则,比SMT方法时隙偏移offset分布更加集中,更靠近LCM前端,体现在调度表中消息排列更为紧凑,更好地保证了TT消息传输的确定性和实时性.
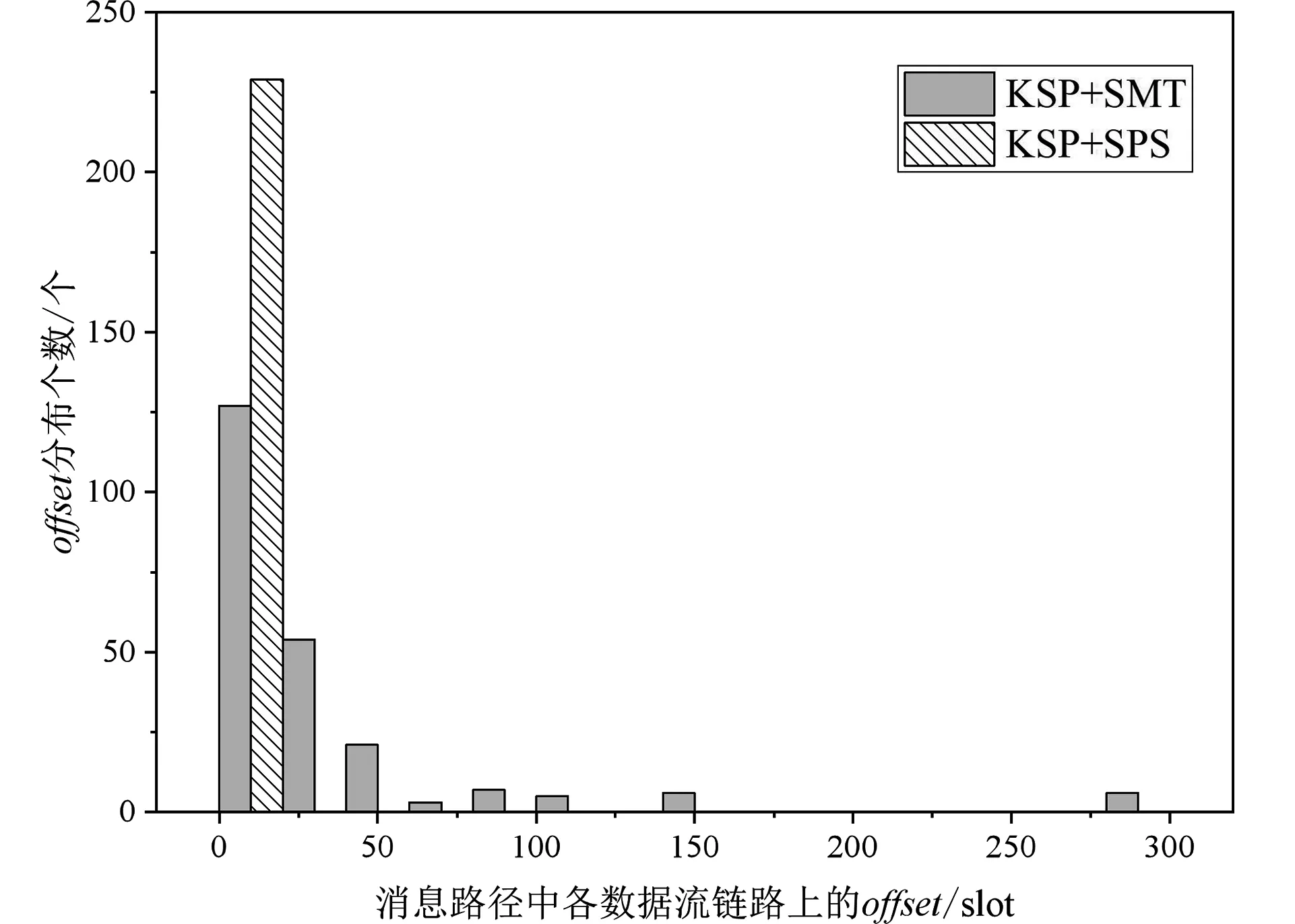
图7 时隙偏移分布直方图
4.2.2 评估指标与分析 调度方法的关键评估指标包括:计算时间指标、延时指标和负载指标.

图8 时隙偏移分布曲线
上述四种方法在不同规模的消息数据下的计算时间的比较结果如表3所示,其中每个单元格里的上下两个数据分别是路径规划时间和时序规划时间.通过比较可知,路径规划方法的计算时间都是多项式级别的,而SMT方法的计算时间呈现指数型增长.当消息规模为496时,SMT方法很难得出结果.SPS方法的计算时间大多较短,且在消息规模为496时计算时间仍远小于1 s.因此,相比于DIJ+SMT和KSP+SMT方法,KSP+SPS方法能够有效减少大规模消息的计算时间.虽然DIJ算法耗时比KSP方法少,但当方法流量不均匀时,DIJ算法更容易出现路径阻塞的现象,导致调度表生成失败.因此,为了保证调度表生成方法的适应性,KSP+SPS方法比DIJ+SPS方法更适用于复杂拓扑下大规模消息数据传输的场景.

表3 计算时间的对比(单位:s)
延时指标包括平均延时Da和平均延时百分比Dap.假设各个消息的传输截止时间为其周期.则该指标可通过下面两式进行计算:
(9)
(10)
其中,消息个数为N,offseti,last为消息传输最后一条路径上的偏移时隙.四种方法在不同规模消息数据下的延时指标比较结果参见表4,可以看到,四种方法的延时百分比相差不大,KSP+SPS方法的表现好于两种SMT方法,与DIJ+SPS方法基本持平.因此,KSP+SPS方法能够较好地满足消息的确定性和实时性需求.
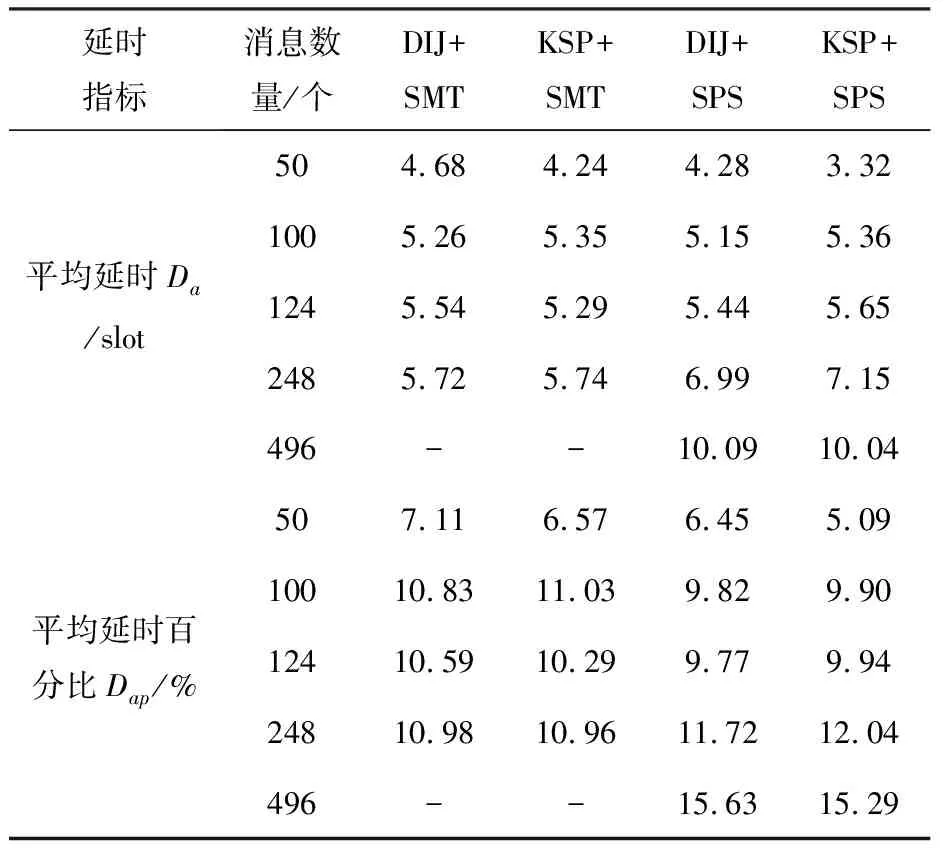
表4 延时指标对比
消息负载指标包括网络链路最大负载BDmax、平均负载BDavg、负载标准差BDsigm和网络链路负载分布直方图,由于网络负载之和不变,若链路数量相同则平均负载结果相同,为了对比方法效果平均负载和负载标准差的计算剔除了负载为0的链路.两种路径规划方法在不同消息规模下的网络链路最大负载、平均负载和负载标准差如表5所示,在消息规模248和496下的链路负载分布直方图对比结果如图9和图10所示.
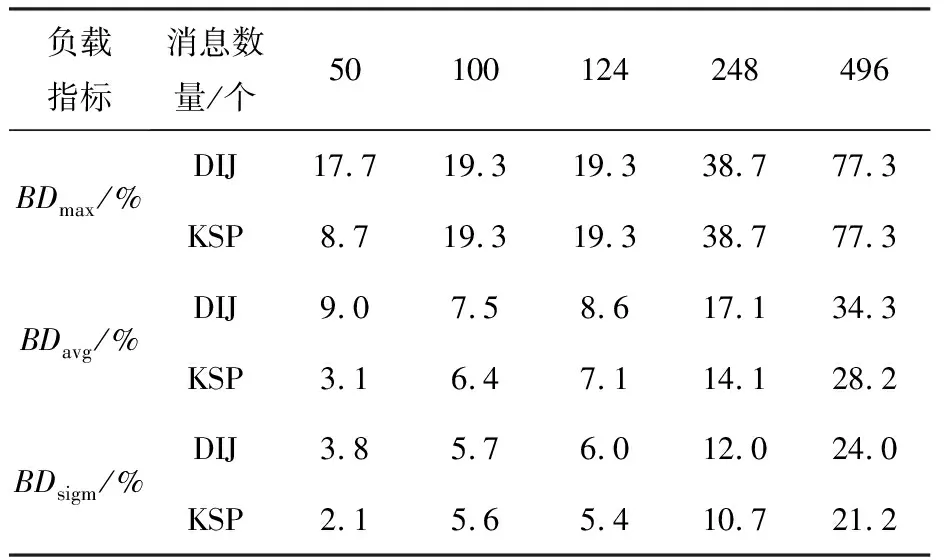
表5 网络链路负载指标对比
由表5中的BDmax数据可知,对于本文研究的拓扑而言,最短路径方法和负载均衡方法对于网络链路最大负载的影响都很小.这是由于某些消息调度任务的路径唯一导致一些主干链路上的负载难以缓解.但是,通过负载均衡方法能够缓解路径不唯一的消息调度任务带来的负载影响.由表5中的BDavg,BDsigm可以看出,KSP方法的负载平均值和负载标准差均小于DIJ算法.这表明KSP方法平均负载更小且负载分布更为均衡.进一步,由图9和图10可以看出,绿色的KSP方法较小负载的频率分布高于红色的DIJ算法,红色的DIJ算法较大负载的频率分布高于或持平绿色的KSP方法,且DIJ算法中负载为0的链路也多于KSP方法.可见, 本文所设计的基于负载均衡的路径规划方法均衡负载的效果较为显著,能够较好满足机载网络中非TT消息传输的负载需求.
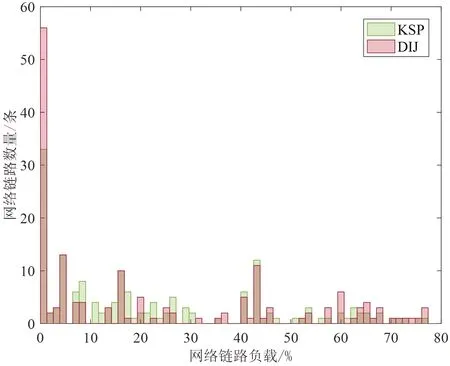
图9 链路负载频率分布直方图(消息数量=496)
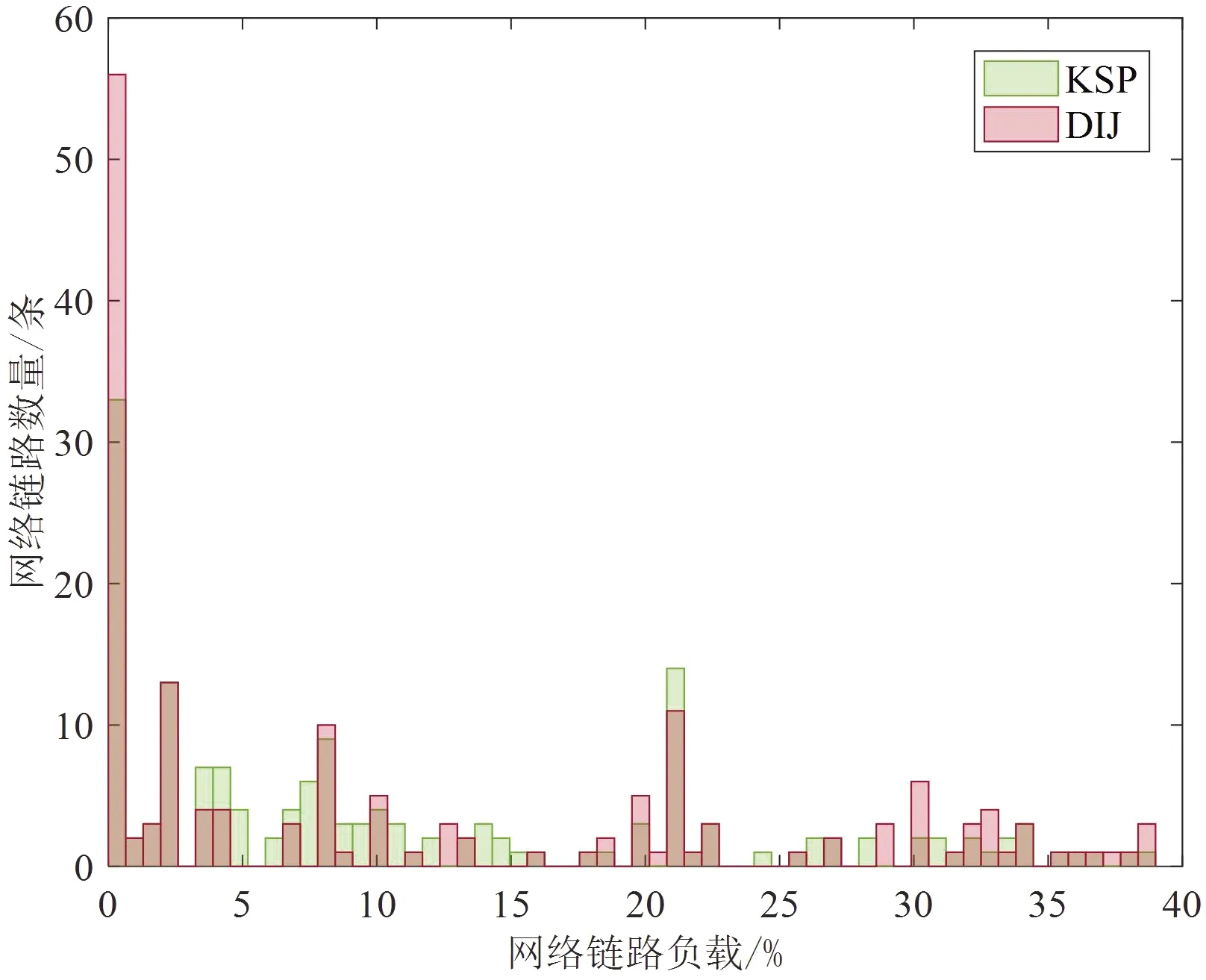
图10 链路负载频率分布直方图(消息数量=248)
5 结 论
未来的机载网络拓扑趋于更加复杂、数据量更大,对调度表生成速度及负载可靠性要求更高.本文提出了一种基于负载均衡的TTE消息调度表生成方法,该方法结合消息长度和负载的影响选取负载均衡的路径规划结果,根据优先级评估值以“背靠背”原则为基础计算消息的时间偏移,实现了对负载均衡的路径规划与时序规划问题的联合求解.在平均负载、负载标准差方面比传统的DIJ算法提升了10%以上,改善了链路的负载均衡状况.同时,计算效率比SMT方法提升2到3个数量级,而延时指标与传统方法则在同一个量级,能保证消息传输的实时性.
综上,该方法在改善链路负载的同时提高了调度表生成的效率,能够满足更高的TT消息实时性和确定性需求,为机载TTE网络负载均衡和调度表生成提供了一种可行的解决方案.

