流动隐身衣的均匀化设计与减阻特性*
王浩 姚能智 王斌 王学生
(华东理工大学机械与动力工程学院,上海 200237)
1 引言
2006 年,Pendry 等[1]证明了麦克斯韦方程组满足空间坐标变换的形式不变性,利用空间变换理论使光可以像流体一样绕过物体传播,实现了物体的隐身效果并提出光学隐身衣概念[2-4].随后,众多学者将变换理论拓展到了不同的领域,其中包括声学[5-10]、热学[11-24]、力学[25-28]等.流动隐身衣与光学隐身衣类似,流体在流经隐身衣时也会主动绕道而行且不干扰流场.也正是其主动绕道而行的特性使得被隐身衣包裹的物体所承受的表面阻力显著降低,这赋予了流动隐身衣在降低能耗、抵抗恶劣环境以及伪装军事目标等方面的巨大潜力,十分具有研究意义.但是如何有效地调控流体绕过物体而不扰动流场目前还少有研究.
为此,Urzhumov 和Smith[29,30]利用达西定律和Brinkman-Stokes 方程所具有的空间坐标变换形式不变性提出了流体动力学隐身衣(简写为流动隐身衣)的概念,并基于流动超材料设计理论构造各向异性的渗透率实现了流体在多孔介质中的隐身流动.然而,这种流动隐身衣因为需要负渗透率的多孔介质被认为难以实现.随后,Li 等[31]通过坐标变换设计梯度深剖面结构并利用实验验证了两个可以用于聚集水波的环形装置.Zou 等[32]受电磁波导隐身衣的启发设计了一种梯度深剖面宽频带隐身衣,在实验中实现了水波隐身.可是水波的传播方式与流体的流动方式大相径庭,这种水波隐身衣仍然无法有效调控流体流动.Tay 等[33]独辟蹊径,通过改变流域高度,不需要超材料即可实现流动隐身效果.Park 等[34]近期证明了流体动力学控制方程在一定约束条件下也同样满足空间坐标变换的形式不变性,并基于此建立起变换流体动力学.通过在流场中放置具有不同大小和方向的微米柱以获得各向异性的动力粘度μ,成功调控了流体流动,完成了流动隐身衣实验.基于变换流体动力学,Park 等[35]随后又通过理论与实验设计了具有不同功能的流动旋转隐身衣、流动聚集隐身衣[36]等流动超材料.此外,Wang 等[37]与Boyko 等[38]利用流变学特性,通过施加温度场、电场等方式均实现了流动隐身效果,但是这两种方式都需要对流场持续输入额外能量才能实现.
基于变换理论设计隐身衣已经有了令人欣喜的结果.然而在此之前,无论是在光学[1,2]、热学[12,18]还是流体动力学[34,36]中,大多数基于坐标变换设计的隐身衣都具有非均匀各向异性的设计参数,这使得我们在实际制备隐身衣时充满了挑战.而本文基于变换流体动力学求解得到流动隐身衣的设计参数,利用等效介质理论与积分中值定理将设计参数简化,得到了流动隐身衣的均匀各向异性设计参数.通过数值模拟证明了使用该均匀参数设计的均匀流动隐身衣,在不同流场中具有与非均匀流动隐身衣一样的隐身效果.利用均匀参数设计制备流动隐身衣将大大降低实际制备难度,同时这一简化方法也可以拓展到其他领域,如力学[20]、热学[12,18]、光学[1,4]、电磁学[2]与声学[5,6]等.此外,本文基于流动隐身衣在不同流场中的适用性设计了一种流动伪装装置,它可以将任意物体的流场伪装成多个其他物体的流场,即可以将隐藏物体的流场分布伪装成由其他物体所引起的期望流场分布.这种流动伪装装置实现了流场中任意物体的流场伪装,为设计流动伪装提供了新方法.最后,当雷诺数不断增加,计算流域脱离蠕动流进入非蠕动流(层流范围内)时,本文定量对比分析了均匀流动隐身衣的隐身效果.又考虑到流动隐身衣的实际设计意义,本文分析对比了均匀流动隐身衣所具有的减阻效率.结果表明,本文所设计的均匀流动隐身衣在非蠕动流中仍然具有较好的隐身性能与减阻性能.
2 均匀流动隐身衣的参数设计
在蠕动流情况下,对于不可压缩的稳态流动,流体运动的连续性方程与动量守恒方程可表示为

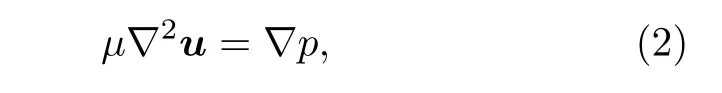
其中u,μ,p分别表示速度矢量、流体动力粘度与压强.研究结果[18,34]表明,在蠕动流中方程(1)和方程(2)的确满足空间坐标变换的不变性.根据变换流体动力学,通过引入雅阁比空间变换矩阵(J)可以将方程(1)和方程(2)从虚拟空间x(x,y,z)变换到物理空间x′(x′,y′,z′),于是有
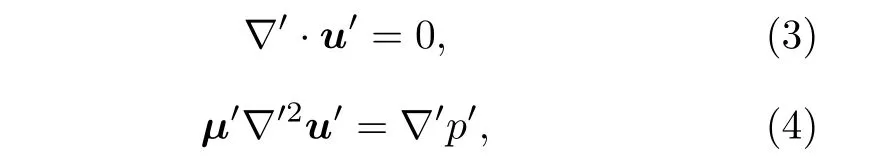
其中u′=Ju/det(J),
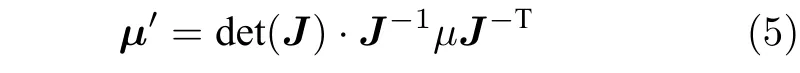
为变换动力粘度,用于调控隐身衣区域流体流动;J-1,J-T分别为雅阁比矩阵的逆矩阵与逆矩阵的转置.
为实现流动隐身,需要对虚拟空间施加流动隐身所需的坐标变换.因此流动隐身衣的空间坐标变换映射关系式可以写成如下形式:
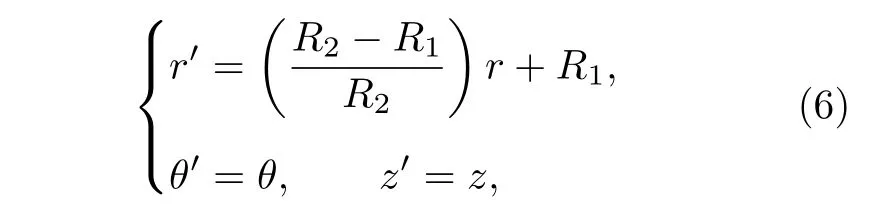
其中R1,R2分别为流动隐身衣的内外半径,如图1(a)所示.根据该映射关系,虚拟空间中心处一点被拉伸成物理空间中的一个半径为R1的圆柱障碍物(r′ <R1),而背景域(r′ >R2)的空间保持不变,作用效果如图1(b) 所示.

图1 模型示意图 (a) 边界条件;(b) 空间坐标变换Fig.1.Schematic models:(a) Boundary conditions;(b) the coordinate transformation.
实现这种作用效果的关键之处,即虚拟空间中的流体流经具有均匀各向异性粘度张量的流动隐身衣时,流体将被压缩进预定义的物理空间中.而这种变换效果则是由(5)式所示的变换粘度引起的,该变换粘度可以表示为[18,34]

值得注意的是,该变换粘度为不均匀各向异性张量,而根据流动超材料的等效介质理论[34-36],依靠微米柱的空间排布规则可使得流体在流经每一层微米柱时都会有不同的流速,继而等效为各向异性的粘 度张量,也即μeff=(〈u0〉s/〈upillar〉s)·μ,其 中upillar与u0分别代 表有无 微米柱 的速度 场,〈·〉s表示平均值,μ为背景流体粘度值.具体的制备方法可以在文献[34]中找到.
不可忽略的是(7)式中的变换粘度在实验室中往往很难设计,这是因为μ′是随半径r′不断变化的.与热学[18,24]、流体动力学[34-36]等领域相同,可以采用一种简化方法得到简化的变换粘度μ′′,将其表示为
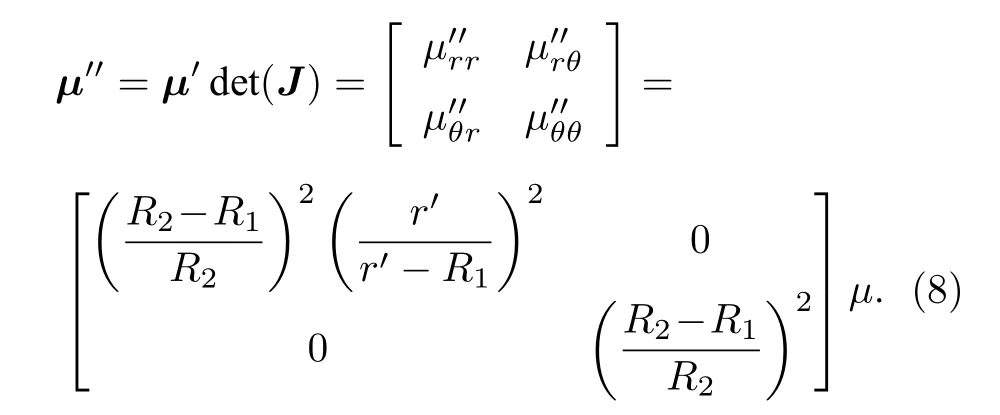
实际上,(8)式在使用时为达到隐身效果还需要乘上补偿系数,该补偿系数可以通过优化获得.经过简化,变换粘度的切向分量便不再随 半径r′变化.但是,变换粘度的径向分量却仍取决于半径r′,这意味着仍然需要非均匀的设计参数.虽然这种经过简化的设计参数可以通过多层流体与微米柱交替的结构实现在流动隐身衣中以阶梯式的方式离散化[34]),但是这仍对制备工艺要求较高.
为了进一步降低制备难度,可以采用等效介质理论与积分中值定理处理简化过的变换粘度.经过计算,可以得到均匀的流动隐身衣,其平均变换粘度为
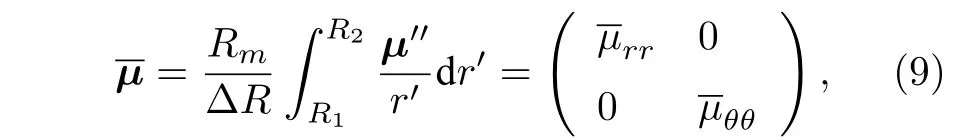
其中Rm=(R1+R2)/2,ΔR=R2-R1,经过积分可以得到


求解定积分还需要代入流动隐身衣的内径R1与外径R2分别作为积分的下限与上限.然而,r′=R1为(10)式的一个奇点,这导致无法将R1作为下限代入(10)式求解径向平均粘度.实际上,在自然界中也并不存在粘度为无穷大的流体.不过由于在r′=R1处为无 滑移固 体壁面(固体壁 面可等效为粘度无穷大的流体),流体无法穿透该壁面,所以此处的等效粘度已经天然满足流动隐身衣对径向粘度值无穷大的要求.于是在求解平均变换粘度时,便可以取壁面R1附近的半径作为积分下限,即NR1(R2/R1>N >1),代入求得定积分结果为
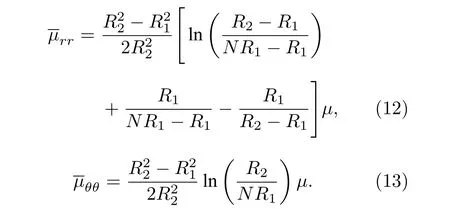

图2 (a)径向粘度与(b)切向粘度随 r ′/R1 的分布Fig.2.Distributions of (a) radial viscosity and (b) azimuthal viscosity with r ′/R1 .
3 数值模拟结果与讨论
根据得到的变换粘度值等式(7)式,(12)式和(13)式,可以使用有限元软件COMSOL Multiphysics 中提供的自定义偏微分方程(Partial Differential Equation,PDE)计算模块验证我们的设计结果.其中,COMSOL 的离散化方案与线性算法采用Galerkin 有限元方法.
如图1(a)所示,流动隐身衣的内外径分别为R1=1.5 cm,R2=3 cm (基于此计算得到N≈1.1).计算流域尺寸为L×H ×D,即是流域长10 cm×高10 cm×深50 μm,其中深度为流域沿z轴的尺寸.由于流域的深度远远小于流域的长度与宽度,即D≪L和H,该流场的流动为Hele-Shaw 流动[39],可以被视为二维流动.流场沿y方向自下向上流动,且进出口压差 Δp=1 kPa (p1>p2) ;流场的左右两边界均为无滑移壁面.此外,计算流域的流体选用室温293.15 K 的水,该流体介质的动力粘度μ=1×10-3Pa · s,密度ρ=9 97.1kg/m3.
图3 所示为均匀背景流场下的速度分布图.图3(a)中给出了背景流场,流场中流线与等压线都平行且均匀分布.当圆柱形障碍物放入流场后,如图3(b)所示,流场中原本平行均匀分布的流线与等压线由于障碍物的干扰变得扭曲.在图3(b)的基础上将非均匀流动隐身衣添加在障碍物周围,如图3(c)所示,在障碍物“穿”上隐身衣之后,位于隐身衣之外(r′ >R2)的流线与等压线又一次恢复到图3(a) 的状态,达到了中心障碍物隐身的效果,这与Park 等[34]设计的非均匀流动隐身衣的作用效果一致.同样地,当使用本文设计的均匀流动隐身衣替换障碍物周围的非均匀流动隐身衣时,如图3(d)所示,隐身衣外的流场也恢复到图3(a)的状态,这表示均匀流动隐身衣具有与非均匀流动隐身衣相同的隐身效果.

图3 均匀流场下的速度分布图,黑色线条为流线,白色线条为等压线 (a) 不含障碍物;(b) 含障碍物;(c) 含障碍物与非均匀隐身衣;(d) 含障碍物与均匀隐身衣Fig.3.Velocity distributions superimposed with streamlines (black color) and isobars (white color) for uniform flow fields:(a) Obstacle absent;(b) obstacle existent;(c) obstacle and inhomogeneous cloak existent;(d) obstacle and homogeneous cloak existent.
为了进一步定量化对比验证所设计的均匀流动隐身衣,可以在r′=R2处取若干点,在背景流场、含非均匀流动隐身衣的流场与含均匀流动隐身衣的流场中分别对这些点的压强进行比较.这些点在隐身衣作用前后压强偏差值的大小,即可用来表示流动隐身衣作用后对背景流场的干扰程度.如图4(a)所示,在计算流域r′=R2处取24 个点进行对比,可以看到这些点在非均匀流动隐身衣与均匀流动隐身衣作用下的压强均与背景流场中该点处的压强重合,这表示我们设计的均匀流动隐身衣与非均匀流动隐身衣一样具有不干扰背景流场的效果.此外,如图4(b)所示,可以取y=0 处流场的速度分布图与背景流场的流速vin进行比较,通过比较确定流动隐身衣外 (|x/R2>1|) 的速度与背景流场的速度值相同,也可证明我们所设计的均匀流动隐身衣具有流动隐身效果.

图4 (a) 压强分布图,黑色线条、红色三角形与蓝色三角形分别表示图3(a)、图3(c)与图3(d)在 r ′=R2 处的压强;(b) 速度分布图,黑色线条、红色线条与蓝色线条分别表示图3(a)、图3(c)与图3(d)在 y=0 处的速度分布Fig.4.(a) Pressure distributions.Black line,red triangle and blue triangle indicate the pressure at r ′=R2 in Fig.3(a) (only background),Fig.3(c) (with inhomogeneous cloaks) and Fig.3(d) (with homogeneous cloaks) respectively.(b) Velocity distributions.Black line,red line and blue line indicate the velocity at y=0 in Fig.3(a) (only background),Fig.3(c) (with inhomogeneous cloaks) and Fig.3(d) (with homogeneous cloaks) respectively.
上述数值模拟验证都是基于均匀背景流场进行的,为了进一步验证所设计的均匀流动隐身衣在非均匀流场中的可行性,将计算流域的进出口边界条件进行修改.分别将进出口边界的左半边与右半边作为新的进出口边界条件并将其余边界均设置为无滑移壁面,进出口压力与其他参数保持不变,得到的数值模拟流场速度分布图如图5 所示.
如图5(a)所示为非均匀背景流场,流场内的流线与等压线不再均匀分布.将圆柱形障碍物与非均匀流动隐身衣“放入”到该非均匀流场中,如图5(b)所示,同均匀流场一样,流动隐身衣外(r′ >R2)的流线、等压线再一次恢复到图5(a)背景流场中的分布状态.如果采用所设计的均匀流动隐身衣替换图5(b)中的非均匀流动隐身衣,如图5(c)所示,背景流场中的流线、等压线分布状态与图5(a)所示相同,这表示本文设计的均匀流动隐身衣一样可以实现非均匀流场中障碍物的流动隐身效果.
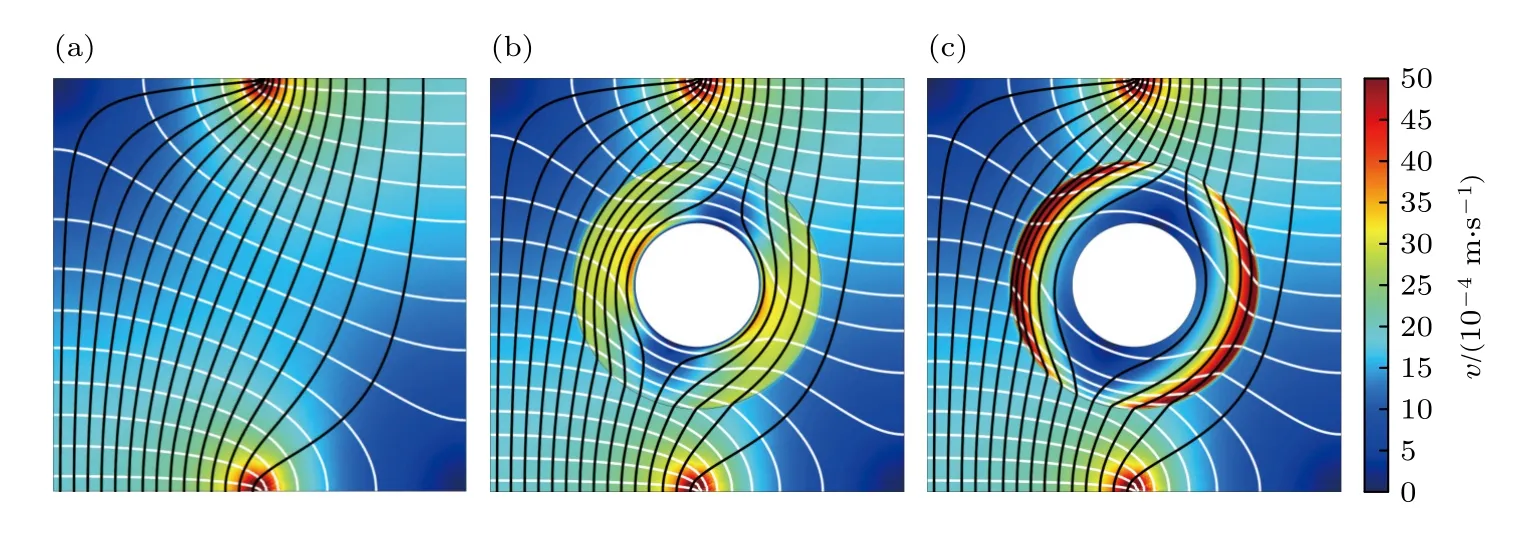
图5 非均匀流场下的速度分布图,黑色线条为流线,白色线条为等压线 (a) 不含障碍物;(b) 含障碍物与非均匀隐身衣;(c) 含障碍物与均匀隐身衣Fig.5.Velocity distributions superimposed with streamlines (black color) and isobars (white color) for non-uniform flow fields:(a) Obstacle absent;(b) obstacle and inhomogeneous cloak existent;(c) obstacle and homogeneous cloak existent.
实际上,流动隐身衣除了可以在流场中隐藏目标以外,还可以实现流场的伪装分布.如图A1 所示,当对指定障碍物进行流动隐身的同时在隐身衣周围放置其他伪装物体,那么隐身衣外流场的表现仅与伪装物体有关,于是可以将指定障碍物隐蔽并将原始流场分布伪装为其他物体的流场分布.
根据上述分析验证,可以确定所设计的均匀流动隐身衣在蠕动流中是有效的.虽然在设计之初并没有考虑对流项(ρu·∇u),但是为了进一步确认所设计的均匀流动隐身衣在雷诺数更大的非蠕动流中是否有效,将在控制方程(2)和方程(4)中加入对流项后做进一步分析验证.而对于定量评定隐身衣的隐身效果,仍然采用与图4(a)类似的办法.在背景流场、含非均匀流动隐身衣的流场与含均匀流动隐身衣的流场中,分别在隐身衣外径R2处取n个点,计算其均方差Ω,可以表示为
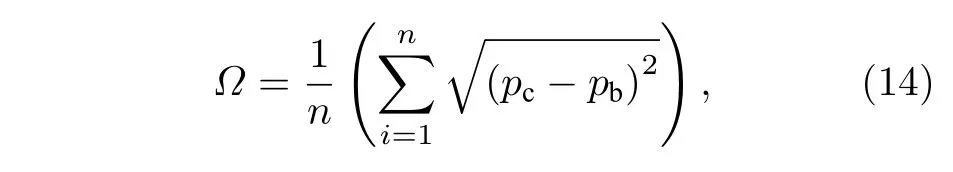
其中pc,pb分别表示含隐身衣流场与不含隐身衣流场中R2处的压强,计算得出的均方差Ω就可以表示放入隐身衣后的流场与纯背景流场的差异程度.如图6 所示,为不同雷诺数下计算得到的均方差,随着雷诺数逐渐增加进入非蠕动流阶段后,无论是均匀隐身衣还是非均匀隐身衣,计算得到的Ω都在持续增加,这表示两种隐身衣的隐身效果都在逐渐降低.这主要是因为此时控制方程中的对流项在起作用,通过方程(1)—(5)(忽略对流项)设计出的流动隐身衣已经不能完美适用.此外,通过数值模拟得到当雷诺数Re=1 与Re=10 时两种流动隐身衣的速度分布图,如图6(c)和图6(d)所示.虽然此时的Ω相比于蠕动流已经增加很多,但流动隐身衣也仍然具有一定适用性.

图6 (a) 隐身效果,其中Ω 表示含隐身衣流场与纯背景流场的差异程度;(b) 减阻效果,其中 ηreduce 表示隐身衣的减阻程度;(c)当流域雷诺数 R e=1 时,非均匀流动隐身衣(c1)与均匀流动隐身衣(c2)的速度分布;(d) 当流域雷诺数 R e=10 时,非均匀流动隐身衣(d1)与均匀流动隐身衣(d2)的速度分布Fig.6.(a) Cloaking effects,in which Ω presents the difference between flow fields with cloaks and pure background flow fields;(b) Drag reduction effects,in which η reduce denotes the degree of drag reduction of cloaks;(c) Velocity distributions of inhomogeneous cloaks (c1) and homogeneous cloaks (c2) at R e=1 ;(d) Velocity distributions of inhomogeneous cloaks (d1) and homogeneous cloaks (d2) at R e=10 .

尽管随着雷诺数的增加,均匀流动隐身衣的隐身性能要比非均匀隐身衣差,如图6(a)所示.但是,流动隐身衣具有的现实意义更偏向于降低隐身对象所受到的流动阻力.因此,为定量分析均匀流动隐身衣的减阻性能,采用阻力计算公式[40]计算隐身障碍物的表面阻力.如图6(b)所示,随着雷诺数的不断增加,虽然已经进入非蠕动流阶段,但是两种流动隐身衣的隐身效率仍然较高,并且均匀流动隐身衣的减阻效率要更好.根据图6,当雷诺数增加时,本文所设计的均匀流动隐身衣相比于非均匀流动隐身衣虽然在隐身效果上有所降低,却拥有了更佳的减阻能力.
4 结论
从变换流体动力学出发,可以得到传统流动隐身衣的设计参数,而该设计参数的非均匀性对实际制备流动隐身衣造成了较大的阻碍.基于此,本文提出了一种将非均匀流动超材料简化为均匀流动超材料的方法,该简化方法利用等效介质理论与积分中值定理,可以得到一组均匀各向异性流动隐身衣的设计参数.通过有限元仿真软件的数值模拟,验证了基于均匀设计参数设计的流动隐身衣与非均匀流动隐身衣具有相同的隐身效果,而且同样适用于多种流场.这种简化非均匀超材料的方法可以拓展到其他领域,采用该方法得到的均匀设计参数将大大降低实际制备超材料的难度,进一步推动超材料的实际应用.此外,基于所设计均匀流动隐身衣对不同流场的适用性,提出了一种可以改变流场分布的流动伪装装置.最后,通过对比分析发现,均匀流动隐身衣的隐身效果随着雷诺数增加而不断降低,尽管不能完美适用于层流流动,但对于缓慢层流流动状态也仍具有一定适用性.通过分析被隐身对象的表面阻力特性发现,均匀流动隐身衣的减阻效率相比于非均匀流动隐身衣要更高.随着雷诺数的不断增加,均匀或非均匀流动隐身衣的减阻性能均有所降低,但仍然都拥有较高的减阻效率,且均匀流动隐身衣的减阻性能更稳定.
附录A 流动伪装装置
图A1(a)所示为原始流场的分布图,流域中心为圆柱形障碍物,此时根据流场分布状态可以轻易地判断出障碍物的位置信息.而当中心障碍物“套上”流动隐身衣后,如图A1(b)所示,此时再根据隐身衣外流场的分布状态就不能确定障碍物的位置.在此基础上将流动隐身衣左右分别添加一个圆柱形物体作为伪装物体,如图A1(c))和(图A1(d)所示,此时流动伪装装置外(红色虚线外的区域)流场的分布状态仅与左右两个伪装物体的位置和大小有关,再根据流场分布状态很难辨别出中心障碍物的位置信息.这样一种具有伪装功能的装置,可以将原始由中心障碍物所产生的流场分布变成伪装物体所产生的流场分布.
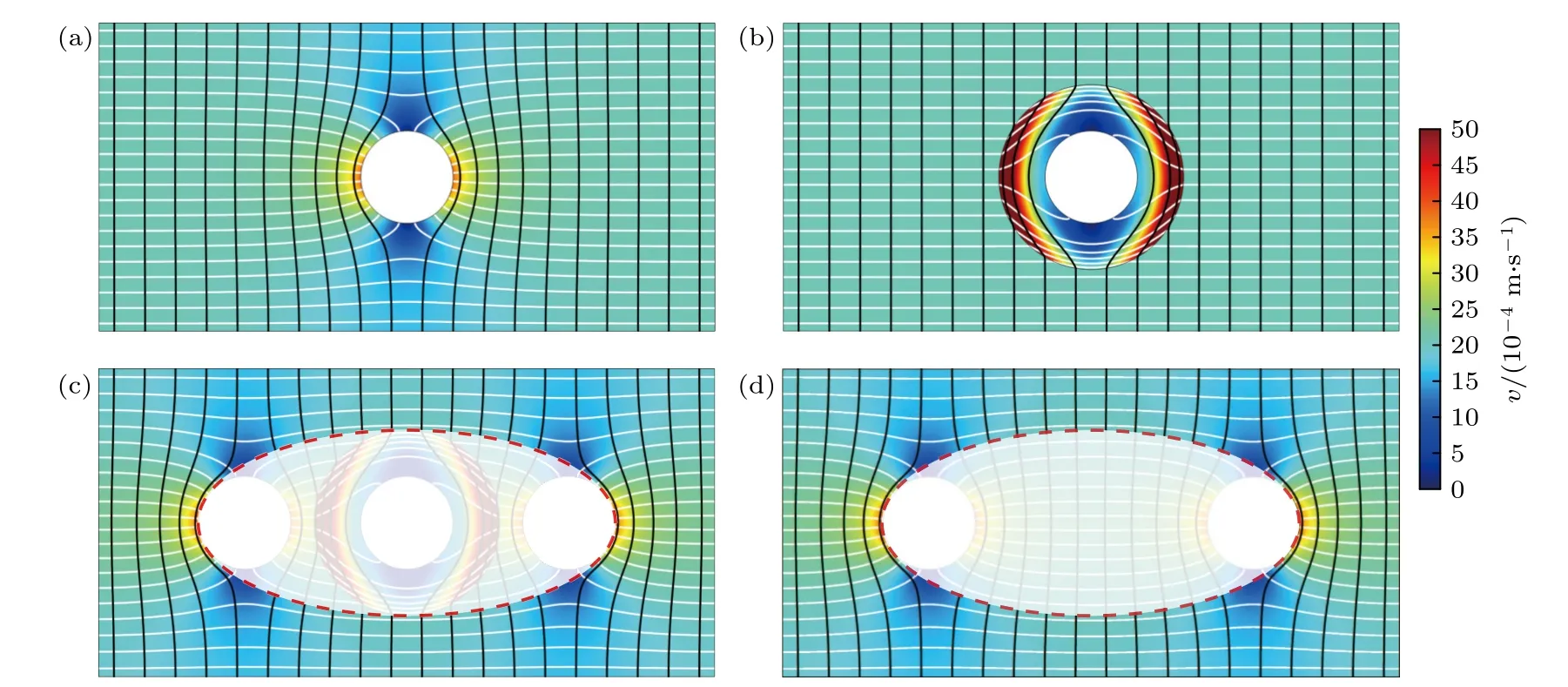
图A1 流动伪装示意图 (a) 仅含障碍物;(b) 隐身状态;(c) 一个障碍物被伪装成两个;(d) 含两个障碍物.从伪装图中可以看出,图(c)红色虚线外的流场与图(d)两个目标物体的流场一致,说明一个物体已经被隐藏并伪装成两个物体Fig.A1.Schematic of hydrodynamic camouflage:(a) Only one obstacle exists;(b) cloaking;(c) one obstacle camouflaged as two obstacles;(d) two obstacles exist.As can be seen from the camouflage devices,the flow fields outside the red dashed line in panel(c) coincide with the flow fields of the two-target objects in panel (d),indicating that one object has been hidden and camouflaged as two objects.

