无人机重力投放展开过程研究

程宇轩, 周洲, 王正平

(西北工业大学 航空学院, 陕西 西安 710072)

空中发射技术是指利用空中发射平台(飞机、飞艇、导弹等)将有效载荷携带到空中,利用发射平台自身的速度和高度实现有效载荷与平台的分离及自主飞行[1]。将空中发射技术应用于无人机起飞阶段,可以达到扩大无人机的作战半径以及提高无人机的生存力和战场突防能力的目的。但是由于空中发射平台上空间有限,无人机需要机翼可收拢来改变空间几何尺寸,改善储存与运输性能,提高包括发射平台与无人机在内的投放系统的机动能力和作战性能[2-3]。然而机翼的收拢在带来有益效果的同时也会带来一些问题。相较于无须收拢展开的传统无人机起飞方式,在储存运输过程中将无人机机翼收拢,意味着在空中投放发射阶段,无人机机翼的展开所带来的额外自由度会使得无人机的动力学模型更为复杂[4]。机翼的大尺度变形还会引起无人机气动参数以及质心、转动惯量等总体参数的变化,这种变化会进一步给无人机的操纵性和稳定性带来影响,严重的甚至会出现失稳。因此针对这种空基投放无人机展开发射阶段的动力学建模与仿真研究显得尤为重要[5]。

由于这种空基重力投放无人机需要在相当大的尺度内改变自身的气动外形,因此不能像常规飞行器那样将其视为单个刚体进行动力学建模,而是需要建立一种包含变形自由度的多体动力学模型[6]。Grant等[7]利用Newton-Euler方程建立了变后掠飞行器的动力学模型,并研究了飞行器的时变惯性效应。Yue等[8]利用Newton-Euler方程建立了折叠翼变形飞行器的非线性动力学模型,并对其进行解耦,研究了飞行器的纵向动力学响应。Seigler等[9]利用Kane方程建立了大型变形飞行器的非线性动力学模型。Obradovic等[10]提出了一种基于Kane方程的变体飞行器动力学模型,并在一种鸥式翼飞行器中进行了仿真验证。Ameri等[11]研究了翼尖形状改变时变体飞机的动力学响应特性。

本文将这种空基重力投放无人机视为一个由机翼、机身等部件组成的多刚体系统,基于Lagrange方程推导并建立对应的多体动力学模型,通过气动的计算结果拟合建立了包含展开角非线性项的气动参数模型,并基于上述模型对空基投放无人机从投放出箱到完全展开的动力学响应进行仿真分析。此外,在相同的控制指令下,对比分析是否考虑无人机展开过程对于空基投放无人机在出箱拉起阶段动力学响应的影响,表明虽然无人机展开速度快用时短,但是展开过程对无人机后续飞行状态的影响不容忽视,也进一步说明了对这一类空基投放无人机出箱投放过程进行研究的必要性。最后,将本文所得的仿真结果与试验数据对比,对比结果进一步说明了本文所建立多体动力学模型的可靠性,并为后续基于动力学模型的控制系统设计提供重要依据,具有一定的参考意义。

1 空基投放无人机多刚体系统模型

本文以某型空基重力投放无人机作为研究对象,基于拉格朗日方程建立投放无人机的动力学模型。如图1所示,假设机体、机身质量均匀分布,几何形状完全对称,机体重心、机翼重心以及机翼和机身的铰接点在同一直线上,即机体与机身之间的相对转动不改变全机质心位置。

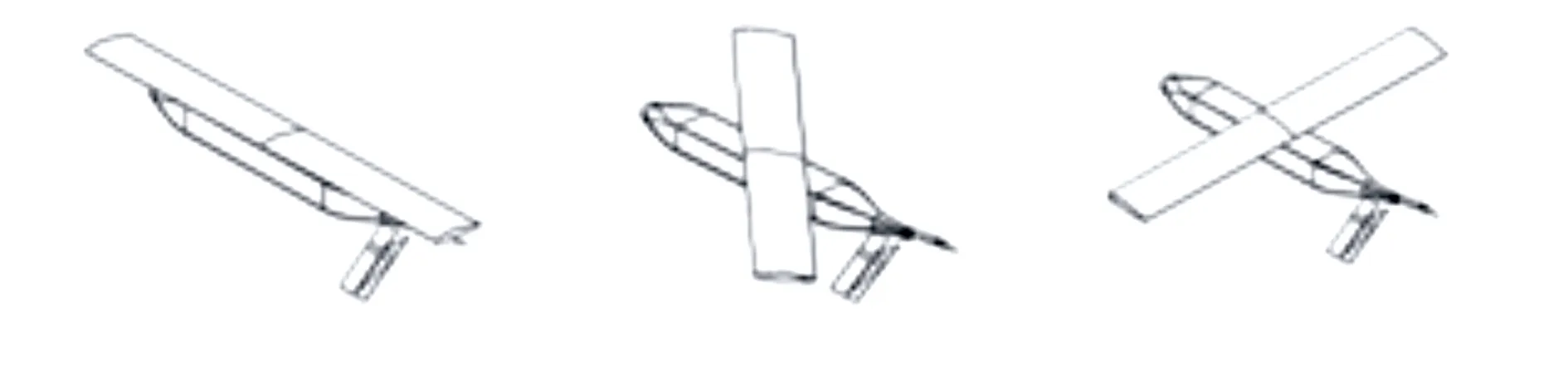
图1 机翼展开过程示意图

1.1 坐标系建立

将机体视为主刚体,机翼视为从刚体,整个系统可以看成由2个刚体组成的多刚体系统,质量分别为mb,mf,其中b表示机体,f表示机翼,总质量为m。

为了描述各刚体的运动,如图2所示定义以下坐标系:

1) 地面坐标系Ogxgygzg:原点Og为地面上固定一点,xg轴指向正北方向,yg轴指向正东方向,zg轴竖直向下指向地心方向。

2) 机体坐标系Obxbybzb:原点Ob取在全机质心,xb轴在飞行器对称面内与飞行器的轴线平行并指向机头方向,yb轴垂直于机体对称面并指向机体右侧,zb轴在飞行器对称面内,与xb轴垂直指向机体下方。

3) 机翼坐标系Ofxfyfzf:原点Of位于机翼重心处,xf轴指向右侧机翼,yf轴指向机翼后缘,zf轴指向机翼下方,与xf轴和yf轴构成右手坐标系。

4) 气流坐标系Oaxayaza:原点Oa取在全机质心,xa轴与飞行器飞行速度矢量的方向重合,za轴在飞行器对称面内并与xa轴垂直指向机体下方,ya轴与xa轴和za轴构成右手坐标系。

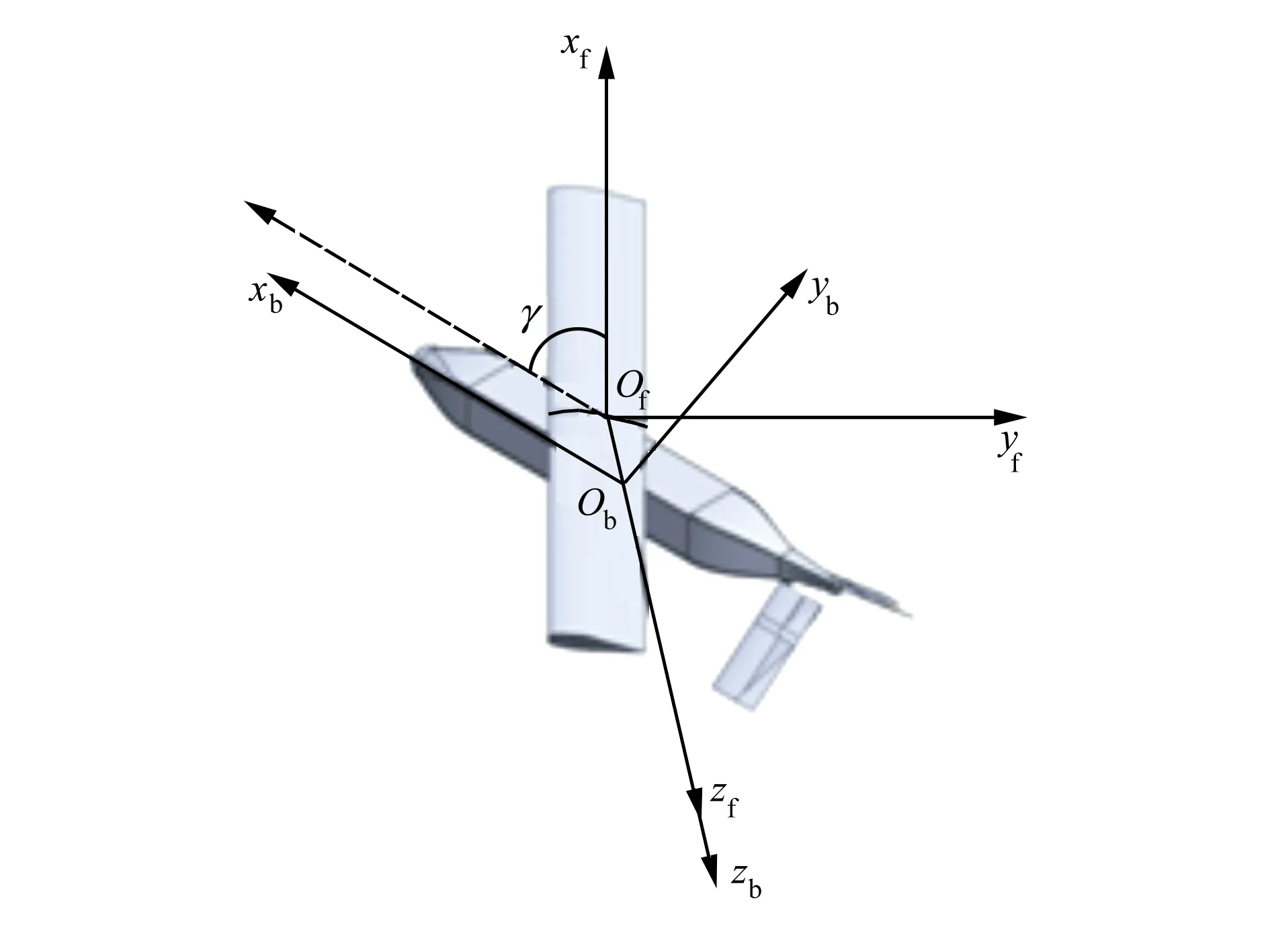
图2 无人机坐标示意图

1.2 广义坐标与广义力

根据广义坐标的定义,刚体系需要构建的广义坐标的数目,等于该刚体系的自由度数目。对于本文中研究的空基重力投放无人机,由2个刚体组成,相对于地面坐标系具有6×2=12个绝对坐标,2个刚体之间的连接方式为铰接,约束个数为5,则刚体系的自由度为12-5=7,对应地需要定义7个适当的广义坐标来描述该系统。

7个广义坐标设为q=[xyzφθψγ]T,其中q(1∶3)=[xyz]T为刚体系的笛卡尔坐标,分别表示机体坐标系相对地面坐标系在xg,yg,zg轴上的位置坐标值;q(4∶6)=[φθψ]T为机体坐标系相对地面坐标系的欧拉角,分别表示俯仰、滚转和偏航;q(7)=γ表示机翼坐标系相对机体坐标系绕zb轴的旋转角度。

根据拉格朗日力学分析,广义力的数目与广义坐标的数目相等,且广义力的量纲与广义坐标的量纲相关。当广义坐标qi的量纲是长度时,对应广义力Qi的量纲就是力的量纲;反之当广义坐标qi的量纲是角度时,对应广义力Qi的量纲就是力矩的量纲。因此Q(1∶3)为刚体系所受力F的广义形式,Q(4∶7)为刚体所受力矩M的广义形式。刚体系所受广义力一般通过虚功原理进行求解。

假设刚体系由刚体y1,y2,…,yl组成,这些刚体的质量分别为m1,m2,…,ml,在各个刚体上施加力fyi,由力fy1,fy2,…,fyl通过虚位移δry1,δry2,…,δryl所作用在刚体系上的虚功可以记为

(1)

而基于拉格朗日方程的动力学建模不考虑约束力及内力做功,因此(1)式可以写成

(2)

式中，fyiex表示刚体yi所受外力。

在(2)式中,虚位移δryi可以写作

(3)

进而虚功的表达式可以写为

(4)

进一步得到

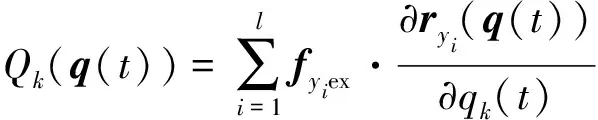
(5)

即为广义坐标所对应的广义力和广义力矩。

广义力和广义力矩也可以写成列向量的形式

对于本文研究的空基投放无人机来说,机体和机翼组成的刚体系统所受外力包括飞行过程中受到的气动力、气动力矩以及机体和机翼之间的扭力弹簧提供的扭转力矩

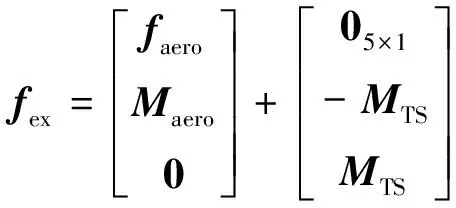
(6)

扭力弹簧所提供的扭转力矩的计算公式为

MTS=kTS·(γ0-γ)

(7)

式中：kTS表示扭力弹簧的刚度系数；γ0表示扭力弹簧预载荷对应的转动角度。

刚体系统所受外力是在机体坐标系Obxbybzb下通过(6)式计算得到的,利用公式(5)将其转换至广义坐标下对应的广义力和广义力矩

Q(q(t))=CQ·fex

(8)

式中，CQ为外力至广义力的转换矩阵

CQ=diag(CGB,CGB,1)

(9)

CGB表示机体坐标系Obxbybzb到地面坐标系Ogxgygzg之间的转换矩阵

(10)

1.3 空基投放无人机的拉格朗日动力学方程

多刚体系统的动力学方程可以根据拉格朗日原理建立,拉格朗日动力学方程以达朗贝尔原理和虚位移原理为基础,是一类基于能量平衡的方程,其具体形式如下所示。

对于任何机械系统,拉格朗日函数L定义为系统总动能T与系统总势能U之差,即

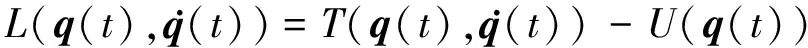
(13)

式中，系统总势能U(q(t))仅与刚体系统的广义坐标相关,与广义坐标的时间变化率无关,因此(13)式可以写成

由于广义坐标是相互独立的,即(15)式对任意δqk均成立的条件是

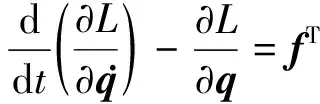
(16)

(16)式即为本文所研究的空基投放无人机多刚体系统无约束的拉格朗日方程。

多刚体系统的动能T可以分为两部分

T=Tv+Tω

(17)

式中：Tv表示多刚体系统质心平动的动能；Tω表示多刚体系统绕质心转动的动能,分别由(18)式和(19)式表示：

式中

对于空基投放无人机来说,其姿态角是指机体坐标系相对惯性坐标系的角度,其导数也是相对惯性坐标系而言,而飞行器的角速度则是绕机体坐标系3个坐标轴旋转的速度,是相对机体坐标系而言的,这一点不同于单纯的姿态角的导数,这也是转换矩阵A存在的原因。

与动能类似,空基投放无人机组成的多刚体系统的势能同样可以分为两部分

U=Ug+UTS

(20)

式中：Ug表示多刚体系统的重力势能；UTS表示扭簧的弹性势能,分别由(21)式和(22)式表示

式中，g表示重力加速度,其余变量同前文定义。

2 空基投放无人机气动力模型

空基投放无人机在收拢展开的变形过程中,作用在无人机上的气动力和气动力矩会随着展开角的变化而发生大幅变化,而且机翼收拢展开的动态运动过程时刻影响着空基投放无人机的气动力,因此很难对其气动特性进行精确的建模。为了在后续的仿真计算和控制器设计过程中较为准确地模拟气动力和气动力矩的变化,本文先利用计算流体力学相关软件,以迎角α、侧滑角β以及机翼和机身之间的夹角γ为变量,得到无人机在不同变量限制的飞行状态下对应的气动力和气动力矩,然后在此基础上,对无人机收拢展开变形的气动力进行非线性化建模。此外,本文采用准定常假设,即假定空基投放无人机的气动力和气动力矩仅与当前飞行状态和构型参数有关,忽略机翼收拢的动态运动对气动特性的影响,最终得到机翼收拢展开过程的气动力和气动力矩如下所示

将所得模型与软件计算结果进行对比以验证模型的可靠性,结果图3～8所示。

图3 阻力系数随迎角变化曲线 图4 升力系数随迎角变化曲线图5 俯仰力矩系数随迎角变化曲线

图6 侧力系数随侧滑角变化曲线 图7 滚转力矩系数随侧图8 偏航力矩系数随侧滑角变化曲线滑角变化曲线

3 仿真结果与动态响应分析

3.1 展开过程仿真结果

为了研究无人机在投放的初始阶段,即展开过程的动力学响应,依据某型空基投放无人机的设计方案及参数,空基投放无人机展开过程的仿真结果如图9～12所示。

从仿真结果可以看出,无人机在出箱后完全展开所需时间为0.8 s,与无人机的飞行总航时相比极为短暂,但是这一过程对无人机后续飞行状态的影响是深远的,不可忽视。从图9可以看出,无人机机身与机翼之间的扭簧同时作用于两者,因此出箱之后机身和机翼会反向旋转,且旋转角度与惯量成反

图9 展开角随时间变化曲线 图10 姿态角随时间变化曲线 图11 气动角随时间变化曲线

图12 高度随时间变化曲线

比。对于仿真所用的空基投放无人机,当机身机翼之间夹角达到90°即展开完成时,机身与投放初始方向夹角为27.2°。

从图10中的俯仰角变化曲线,图11中的迎角变化曲线以及图12的高度变化曲线中可以看出,无人机的展开过程对于其纵向飞行状态不会产生太大影响,且在俯仰力矩的作用下,无人机具有抬头拉平的趋势。

图11中的侧滑角变化曲线说明由于扭簧力矩的作用,展开完成之后无人机的侧滑角达到了27°,图10中的滚转角变化曲线和偏航角变化曲线也体现了无人机在横航向无法保持稳定的飞行状态。

3.2 是否考虑展开过程的对比仿真

为了进一步研究展开过程对无人机后续拉平阶段的影响,在相同的控制指令输入条件下,分别对是否考虑展开过程这2种不同的情况进行仿真。其中不考虑展开过程表示无人机以完全展开即机翼和机身之间夹角为90°的状态开始投放,而考虑展开过程表示无人机投放的初始状态为收拢状态,即机翼和机身之间的夹角为0°。无人机出箱拉起阶段的仿真结果对比如图13～19所示。

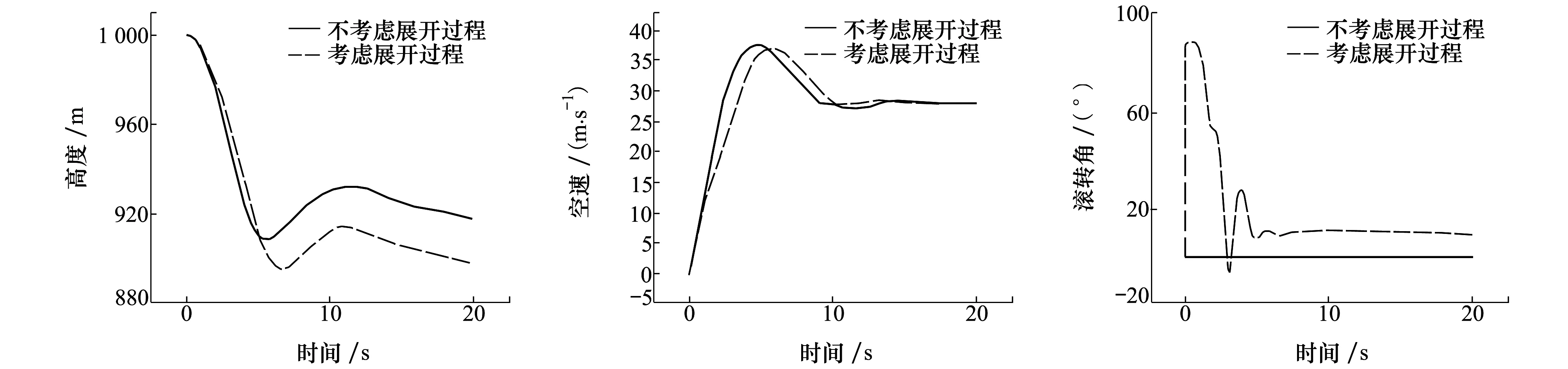
图13 高度随时间变化曲线 图14 空速随时间变化曲线 图15 滚转角随时间变化曲线

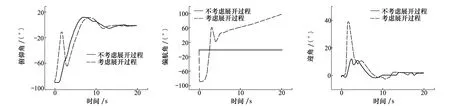
图16 俯仰角随时间变化曲线 图17 偏航角随时间变化曲线 图18 迎角随时间变化曲线

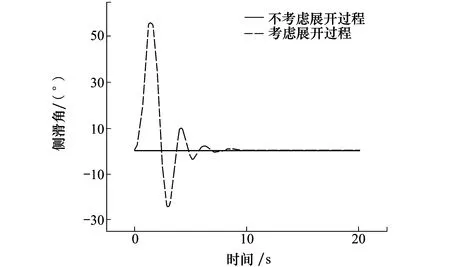
图19 侧滑角随时间变化曲线

图13和图14分别是无人机的高度和空速在出箱拉起阶段随时间的变化曲线,2种不同初始条件下的投放对于空速变化影响不大,考虑展开过程的放会使得拉起后的飞行高度略低于不考虑展开过程的飞行高度。

图15～17是无人机的姿态角随时间的变化曲线,可以明显看出考虑展开过程会使得无人机的姿态角在出箱之后有较大幅度的变化,虽然无人机的俯仰角最终受控达到稳定状态,但是无人机的滚转角最终趋于10°左右,偏航角甚至处于增大的发散状态,可见展开之后应合理控制无人机的滚转角和偏航角,否则会给无人机的投放带来风险甚至是失败的可能。

3.3 数字仿真与飞行试验对比

为了进一步验证本文提出的针对此类空基投放无人机的动力学研究方法的可靠性,提取本文研究对象某次试验中投放改出阶段的数据,并与考虑展开过程的仿真结果进行对比,如图20～22所示。

图20 高度随时间变化曲线 图21 俯仰角随时间变化曲线 图22 空速随时间变化曲线

由图20可见,飞行仿真中无人机投放改出过程的飞行高度与试验值的变化趋势较为接近,且仿真得到无人机最终高度降低了101.3 m,试验值为119 m,相对误差在15%以内。由图21可见,投放改出过程的初期阶段仿真所得俯仰角与试验值相差较大,具体原因在于试验是基于直升机这一动基座进行投放,无人机无法保持静止的初始状态,会以一定的初始角速度进入改出过程。在趋于稳定后,仿真得到无人机的俯仰角为1.4°,试验值为2.4°,误差仅为1°。由图22可见,投放改出过程中,无人机的空速变化仿真结果与试验值的变化趋势也基本一致,且相对误差在10%以内。考虑到本文的动力学模型及仿真无法对试验现场的风速等环境因素进行复现,本文所得仿真结果与试验值之间的误差是合理的,说明本文推导得到的空基投放无人机多体动力学模型是合适可靠的。

4 结 论

1) 基于拉格朗日方程,建立了空基投放无人机的多体动力学模型,模型中的7个广义坐标可以准确表达出空基投放无人机的运动姿态,并求解得到对应的广义力和广义力矩。

2) 考虑无人机机翼与机身相对旋转的影响,可知展开角的存在使得无人机的压力分布不对称,导致常规的气动力模型不再适用。本文引入展开角作为额外变量,建立了空基投放无人机的非线性气动力模型,和气动计算软件结果对比显示所得气动力模型是合适可靠的。

3) 基于空基投放无人机的气动模型和多体动力学模型,进行了展开过程的仿真,并对比了在考虑展开过程的情况下,无人机拉起改出阶段的动力学响应与不考虑展开过程的响应的区别,说明了在此类空基投放无人机的研究过程中,对展开阶段进行研究的必要性。

4) 通过与试验数据的对比,进一步验证了本文建立的多体动力学模型的合理性及可靠性,可为今后基于模型设计控制律提供重要参考和依据。