一类复矩阵方程的双结构解及最佳逼近

黄敬频，徐 云

(广西民族大学 数学与物理学院， 南宁 530006)

0 引言

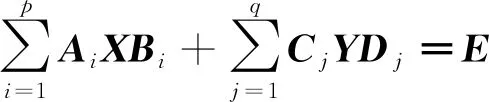
在复数域上讨论方程

(1)

具有三对角-箭形同元双结构解(X,Y)及其最佳逼近问题。

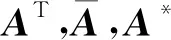
定义1复数域C上2个n级矩阵:

(2)

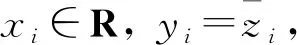
三对角矩阵在船体数学放样中3次样条插值函数的建立，以及微分方程边值问题的求解等方面有重要应用。箭形矩阵来源于孤立分子的无辐射跃迁与费米液体的耦合问题，它可作为非线性调节控制系统中的参数矩阵，也可用来描述星形弹簧质量系统的振动问题。提出并具体讨论如下2个问题：

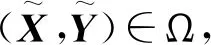
1 问题1的解

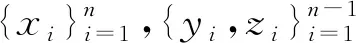
w=(x1,…,xn,y1,…,yn-1,z1,…,zn-1)T∈C3n-2

(3)

引理1设X是形如式(2)的三对角矩阵，ei为单位矩阵In2的第i列，构造一个列正交矩阵T如下：

(4)

则vec(X)=Tw， 其中w,T见式(3)(4)所示。

证明根据定义1和矩阵(4)的构造方法可得

vec(X)=x1e1+…+xie(i-1)n+i+…+xnen2+

y1e2+…+yie(i-1)n+i+1+…+yn-1en2-n+

z1en+1+…+ziein+i+…+zn-1en2-1=

(e1,…,e(i-1)n+i,…,en2)(x1,…,xn)T+

(e2,…,e(i-1)n+i+1,…,en2-n)(y1,…,yn-1)T+

(en+1,…,ein+i,…,en2-1)(z1,…,zn-1)T=

α1(x1，…,xn)T+α2(y1，…,yn-1)T+

α3(z1,…,zn-1)T=(α1,α2,α3)w=Tw

因此引理1关于vec(X)的表达式成立。证毕。

引理2设Y是形如式(2)的箭形矩阵，ei为单位矩阵In2的第i列，构造一个列正交矩阵U：

(5)

则vec(Y)=Uw,其中w,U如式(3)(5)所示。

证明根据定义1和矩阵(5)的构造方法可得

vec(Y)=x1e1+…+xie(i-1)n+i+…+xnen2+

y1e2+…+yiei+1+…+yn-1en+

z1en+1+…+ziein+1+…+zn-1en2-n+1=

(e1,…,e(i-1)n+i,…,en2)(x1,…,xn)T+

(e2,…,ei+1,…,en)(y1,…,yn-1)T+

(en+1,…,ein+1,…,en2-n+1)(z1,…,zn-1)T=

β1(x1,…,xn)T+β2(y1,…,yn-1)T+

β3(z1,…,zn-1)T=(β1,β2,β3)w=Uw

所以引理2关于vec(Y)的表达式成立。证毕。

引理3[3]复矩阵方程AX=B有解的充要条件是AA+B=B。有解时，它的一般解和最小二乘解均可表示为：X=A+B+(I-A+A)V， 其中V是适当阶数的任意矩阵。

引入记号

v=vec(E)

则矩阵方程(1)等价于

F·vec(X)+G·vec(Y)=v

(6)

如果(1)存在解(X,Y)∈TAn，则由引理1和引理2得

vec(X)=Tw,vec(Y)=Uw

其中w、T、U分别如式(3)(4)(5)所示。把vec(X)和vec(Y)代入式(6)得

(FT+GU)w=v

(7)

这里FT+GU∈Cml×(3n-2),v∈Cml。设FT+GU的奇异值分解为

(8)

∑r=diag(σ1,…,σr)>0,P∈Uml×ml,Q∈U(3n-2)×(3n-2)是酉矩阵。令

(9)

其中vr,wr∈Cr,v3n-2-r,w3n-2-r∈C3n-2-r。于是关于问题1的解，有如下结果：

定理1给定Ai,Cj∈Cm×n,Bi,Dj∈Cn×l(i=1,…,q),E∈Cm×l,并设(7)中FT+GU的奇异值分解为式(8)，则方程(1)存在解(X,Y)∈TAn的充要条件是分解式(9)中向量vr=∑rwr,v3n-2-r=0。有解时，它的一般解表达式为

(10)

其中∑r,Q,vr由分解式(8)(9)给出，w3n-2-r∈C3n-2-r是任意向量，解(X,Y)由w唯一确定。

证明方程(1)存在解(X,Y)∈TAn等价于方程(7)关于w有解。又由式(7)(8)(9)可得

因此有vr=∑rwr,v3n-2-r=0。 再由式(9)可得

于是式(1)有解(X,Y)∈TAn的充要条件是vr=∑rwr，v3n-2-r=0，且其通解为(10)。证毕。

在方程(1)中取Cj=0(j=1,…,q)或Ai=0(i=1,…,p),并由方程组(7)及引理3可得以下2个推论。

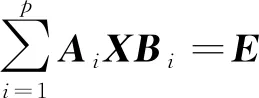
wt=(FT)+v+(I3n-2-(FT)+FT)γt

其中γt∈C3n-2是任意向量，解X由wt所确定。

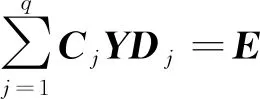
wa=(GU)+v+(I3n-2-(GU)+GU)γa

其中γa∈C3n-2是任意向量，解Y由wa所确定。

下面讨论方程(1)在HTAn中的解。先对复矩阵Ai,Cj,Bi,Dj(i=1,…,p;j=1,…,q),E及X,Y作实分解为：

Ai=Ai0+Ai1I,Cj=Cj0+Cj1I

Bi=Bi0+Bi1I,Dj=Dj0+Dj1I

E=E0+E1I,X=X0+X1I,Y=Y0+Y1I

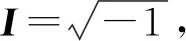
(11)

引入记号

(12)

则方程组(11)等价于

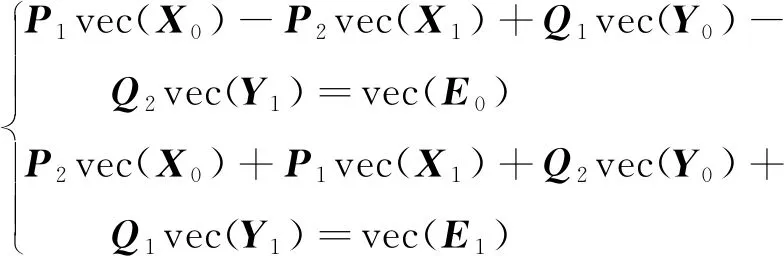
(13)

当(X,Y)∈HTAn时，由X=X*,Y=Y*可得

因此(X0,Y0)及(X1,Y1)分别由下列2个实向量唯一确定

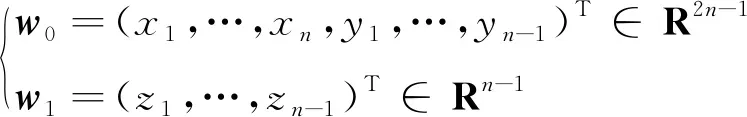
(14)

类似于引理1和引理2的方法，设ei为单位矩阵In2的第i列，构造矩阵T0、U0、T1、U1：

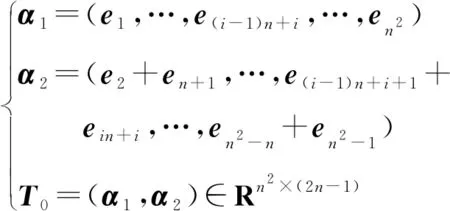
(15)

(16)

T1=(en+1-e2,…,ein+i-e(i-1)n+i+1,…,

en2-1-en2-n)

(17)

U1=(en+1-e2,…,ein+1-ei+1,…,

en2-n+1-en)

(18)

其中T1,U1∈Rn2×(n-1)。于是有

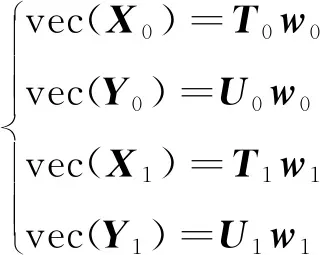
(19)

将式(19)代入式(13)整理得

Hwh=vh

(20)

其中

于是关于方程(1)在HTAn中的解，有如下结果：

定理2给定Ai,Cj∈Cm×n,Bi,Dj∈Cn×l(i=1,…,p；j=1,…,q),E∈Cm×l,则方程(1)存在Hermite三对角-箭形同元双结构解(X,Y)∈HTAn的充要条件是

HH+vh=vh

(21)

有解时，它的一般解表达式为

wh=H+vh+(I3n-2-H+H)γh

(22)

其中γh∈R3n-2是任意向量，解X、Y由wh所确定。

证明方程(1)存在解(X,Y)∈HTAn等价于方程(20)关于wh有解，于是根据引理3可知(1)存在解(X,Y)∈HTAn的充要条件是式(21)成立，且其通解由式(22)给出。证毕。

根据定理2的结果，容易得到以下推论3和推论4。

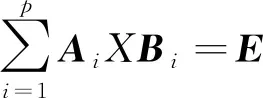
有解时，它的一般解表达式为

其中γht∈R3n-2是任意向量，解X由wht所确定。

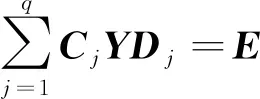
有解时，它的一般解表达式为

其中γha∈R3n-2是任意向量，解Y由wha所确定。

2 问题2的解

假定方程(1)存在解(X,Y)∈TAn,即定理1中解集w非空。对于给定的三对角矩阵M和箭形矩阵N，设它们对应的3n-2维向量为

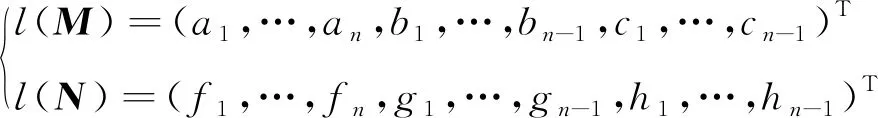
(23)

并对向量Ql(M)和Ql(N)分解如下

(24)

这里Q∈U(3n-2)×(3n-2)是由式(8)给出的酉矩阵。于是关于问题2的解，有如下结果：

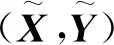
(25)

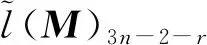
证明根据矩阵(X,Y)的向量化表示式(3)及定理1可得

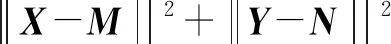
其中w3n-2-r∈C3n-2-r是待定向量，因此有

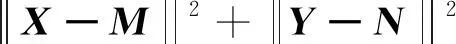
当且仅当

(26)

利用Frobenius范数定义及二元函数极值方法，容易求得式(26)关于w3n-2-r具有唯一解

(27)

把式(27)代入式(10)即得表达式(25)。证毕。

3 数值算例

给定矩阵A,C∈C2×4,B,D∈C4×2,E∈C2×2，试用本文方法判断方程AXB+CYD=E是否存在解(X,Y)∈TA4或(X,Y)∈HTA4。

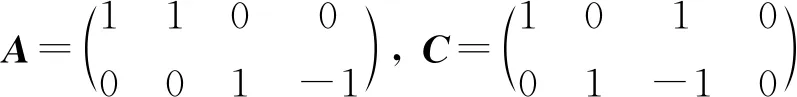
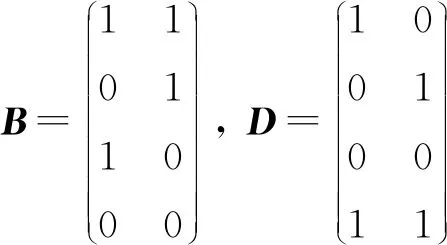
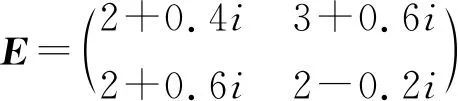
判断是否存在解(X,Y)∈TA4。根据引理1和引理2及(7)写出T,U,F,G,v如下：

T=(e1,e6,e11,e16,e2,e7,e12,e5,e10,e15)

U=(e1,e6,e11,e16,e2,e3,e4,e5,e9,e13)

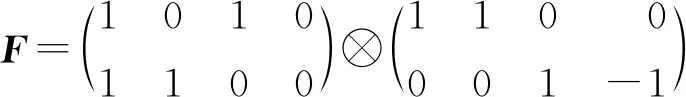
v=vec(E)

其中ei为单位矩阵I16的第i列。直接计算可得

(FT+GU)(FT+GU)+v=v

因此，根据定理1知，方程AXB+CYD=E存在三对角-箭形双结构解(X,Y)∈TA4且由式(10)确定。

判断是否存在解(X,Y)∈HTA4。先按方程(20)写出H,vh。由于

P1=BT⊗A,P2=0,Q1=DT⊗C,Q2=0

E=E0+E1I

T0=(e1,e6,e11,e16,e2+e5,e7+e10,e12+e15)

U0=(e1,e6,e11,e16,e2+e5,e3+e9,e4+e13)

T1=(e5-e2,e10-e7,e15-e12)

U1=(e5-e2,e9-e3,e13-e4)

于是

vh=(2,2,3,2,0.4,0.6,0.6,-0.2)T∈R8

直接计算可得HH+vh=vh，因此根据定理2可知，方程AXB+CYD=E存在解(X,Y)∈HTA4且由式(22)确定。下面给出其中1组解

4 结论

复系统(1)是一类涵盖Sylvester方程和Lyapunov方程，具有广泛实际背景的矩阵方程，本文研究了它的三对角-箭形同元双结构解及最佳逼近问题。针对问题1，主要利用三对角矩阵和箭形矩阵的结构特点，给出它们的向量化刻划，获得原方程在TAn和HTAn中有解的充要条件及其解表达式。针对问题2，利用结构矩阵的向量化技巧及Frobenius范数酉矩阵乘积不变性，在问题1解集Ω≠∅条件下，获得问题2的最佳逼近解。数值算例验证了本文结果的正确性。