横断山区森林土壤饱和导水率传递函数的评价与构建研究①
孙志祥,崔俊芳*,杨汝馨,唐翔宇,王根绪
横断山区森林土壤饱和导水率传递函数的评价与构建研究①
孙志祥1,2,崔俊芳1*,杨汝馨1,2,唐翔宇1,王根绪3
(1 中国科学院、水利部成都山地灾害与环境研究所,成都 610041;2 中国科学院大学,北京 100049;3 四川大学水力学与山区河流开发保护重点实验室,成都 610207)
利用国际上具有代表性的9种土壤饱和导水率(s)传递函数模型估算了横断山地区贡嘎山不同类型森林土壤的s,并与实测数据进行了比较,结果表明,现有模型在横断山地区的拟合结果与实测数据的偏差极大,其在研究区的适用性差。结合研究区土壤含石率偏高的特点,增加土壤石砾含量(粒径 >2 mm)作为输入变量,同时选取土壤容重、有机质含量和颗粒分布3种土壤基本特性参数作为输入变量,构建了本区域s传递函数模型:s= 9.48 + 12.32×BD + 0.29×SOM – 1.94×GF + 2.89×silt – 5.34×sand,结果显示,模型预测值与实测值相关系数为0.67,该模型可以作为横断山地区自然林地s传递函数使用,从而为山地森林水文过程和自然灾害预警研究提供实用的参数估算工具。
森林土壤;饱和导水率;传递函数;横断山地区
土壤通过入渗、蒸散发、地表径流和地下水补给等途径调节水分平衡,从而对区域和全球地表水分和能量平衡产生重大影响[1-2]。土壤饱和导水率(soil saturated hydraulic conductivity,s)是研究地下水产流机制、径流发生以及土体可蚀性的重要参数。传统获取s值是通过原位测量或野外取样进行室内测定的方式获得,所获数据准确性高,但该方法成本高、耗时耗力,同时由于s较大的空间变异性,所测数据很难应用到大区域范围内[3]。1989年荷兰土壤学家Bouma[4]首次提出传递函数(pedo-transfer functions,PTFs)的概念,旨在通过大量数据建立土壤易获取性质(有机质、质地、容重等)与土壤水力学参数之间的关系,间接计算土壤水力学参数。传递函数的提出弥补了大量土壤水力学参数的缺失值,大大促进了土壤水分运动、溶质迁移和土壤侵蚀的研究[5]。近半个世纪,尤其是近30年来,科研工作者围绕s传递函数做了大量的研究工作,取得了丰硕的研究成果,也提出了基于不同因子的传递函数。Campbell和Shiozawa[6]根据英国大量的土壤样本数据,将土壤容重和颗粒大小分布作为因子构建土壤传递函数用于预测s;Wang等[7]利用青藏高原382个土壤数据,将土壤粒径分布、容重、有机碳含量以及首次加入纬度作为输入因子建立了s传递函数;同样,Zhang和Schaap[8]根据1 306个土壤数据,采用神经网络方法分别建立了将土壤颗粒分布、容重、田间持水量作为输入因子的多个传递函数并用于预测s。然而,影响s的因素极其复杂,其中土壤类型、质地、结构以及土壤大孔隙是影响s的主要因素[9-11],同时s还受区域气候以及土地利用类型的影响[12-13],导致s呈现极大的时空变异性。因此,在采用土壤传递函数预测s时,需要进行区域验证。
横断山地区位于四川盆地西部、云贵高原西北部和青藏高原东部,处于中国第一、二级地势阶梯的过渡部位,属高山峡谷地貌。区内地形地貌、气象水文、地质构造等地质环境条件复杂,土壤侵蚀严重,出露的岩层主要有三叠系上统灰白色砂板岩夹少许灰岩,第四纪松散沉积物质组成为古河床沉积形成的砂、卵石层,岩体较为破碎,风化强烈[14],在暴雨季节,崩塌、滑坡、泥石流爆发频繁,严重威胁居民生命安全及重大工程建设[15-16]。s是横断山地区土壤水分运动、自然灾害预测的重要参数[17]。然而,关于横断山地区s的相关研究鲜有报道,且目前在横断山地区水力学参数指标的可用数据非常有限[18-20]。战海霞[21]的研究发现,横断山地区土壤多为林地土壤,土体结构松散,根系发达且石砾含量高,土壤大孔隙结构丰富,由此导致的土体渗透系数高达25 mm/min。因此,现有的s传递函数在该类土壤s参数估算上有待验证。基于此,本研究结合研究区土壤含石率偏高的特点,增加土壤石砾含量(粒径 >2 mm)作为输入变量,同时选取土壤容重、有机质含量和颗粒分布3种土壤基本特性参数作为输入变量,拟构建本区域s传递函数模型。
1 材料与方法
1.1 研究区概况
本研究以贡嘎山海螺沟流域(29°20′ ~ 30°20′ N,101°30′ ~ 102°15′ E)为研究区。贡嘎山位于青藏高原东缘,主峰海拔7 556 m,是横断山地区的最高峰,区域内地势总体呈东西两侧和北面高、中部和东南部低的趋势,岭谷高差一般1 500 ~ 3 000 m,各支沟狭窄,多呈“V”型谷,谷坡坡度多35° ~ 55°;在支沟和主沟交汇处相对开阔,坡度较支沟两岸处低缓,为25° ~ 35°[22]。该区域属于亚热带季风气候区,年均气温4.1 ℃,年均降水量1 903 mm,雪线和林线分别位于海拔4 900 m和3 700 m附近[23]。海螺沟流域属于典型山地生态系统,垂直气候带完整,随海拔升高,依次为亚热带、暖温带、寒温带、亚寒带、寒带等不同气候类型[24]。同时随着气候类型不同,形成明显的植被带,其中,1 900 ~ 2 200 m是阔叶林带,年降水量约2 000 mm,土壤类型为棕壤,植被以苞槲柯()为优势种;海拔2 200 ~ 2 800 m为针阔混交林带,年降水量2 500 mm,土壤类型为暗棕壤,植被有铁杉()、槭树(r)、桦树()等组成;海拔2 800 ~ 3 600 m为针叶林带,年降水量2 800 ~ 3 100 mm,土壤类型为山地灰化土,主要树种以麦吊杉()和峨眉冷杉()为主。研究区土壤均具有粗骨性强、土薄、石砾含量丰富的基本特征[25-26]。
1.2 样品采集与分析
于2019年8月在海螺沟流域开展野外调查,在常绿阔叶林、针阔混交林、针叶林3种植被带各选取3块代表性样地,除去地表凋落物后,每个样地挖一个1 m深的土壤剖面。每个剖面分四层(0 ~ 10、10 ~ 20、20 ~ 50和50 ~ 100 cm),用环刀(高度5 cm,直径5 cm,体积100 cm3)取原状土样用于测定土壤容重、石砾含量和s;并在环刀周围0 ~ 20 cm范围内采集土样,带回实验室自然风干后研磨分别过0.25 mm和2 mm筛孔用于土壤有机质和颗粒组成的测定。s利用定水头下的马氏瓶渗透仪进行测定[27],容重采用环刀烘干法测定[28],石砾含量以环刀内土样的全部石砾(粒径>2 mm)与环刀内全部土样的体积百分比计算,土壤有机质采用重铬酸钾外加热法测定[29],土壤颗粒组成采用吸管法测定[30],土壤颗粒粒级按照美国制土壤颗粒组成分组,分为3级:0.05 ~ 2 mm砂粒,0.002 ~ 0.05 mm粉粒和<0.002 mm黏粒。
1.3 研究方法
本研究利用Excel 2010及SPSS 22.0对研究区所测得土壤参数进行基本统计分析,并将研究区实测数据分别代入不同土壤传递函数模型中进行计算,比较估算值与实测值的误差,采用平均误差(ME)、均方根误差(RMSE)、决定系数(2)评价传统土壤传递函数的预测精度。在此基础上,选取土壤容重、石砾含量、有机质含量、土壤粒径组成作为输入参数,利用相关分析、主成分分析和多元逐步回归分析研究s的主要影响因素,建立横断山地区森林土壤s传递函数。
本研究所选取的9种经典传递函数包括Weynants模型[31]、Cosby模型[32]、Wosten模型[33]、Campbell模型[6]、Pucket模型[34]、Vereecken模型[35]、Saxton模型[36]、Julià模型[37]、Ahuja模型[38],其具体的函数表达式见表1。
新建传递函数的具体构建步骤如下:①建立多元回归模型=a + b×1+ c×2+ d×3(a、b、c分别为各自变量1、2、3的回归系数);②回归系数显著性检验,将不显著变量剔除,再次进行回归;回归方程显著性检验,确保<0.05;③模型检验:进行模型多重共线性检验,如果变量之间存在共线性,则剔除该变量;自相关检验,消除自相关带来的误差;④重复以上步骤① ~ ③,直至模型中各自变量与因变量达到统计学意义上的显著相关。

表1 研究采用的土壤传递函数
注:式中s为饱和导水率(mm/min);sand、silt、clay分别为土壤砂粒、粉粒和黏粒的含量(以质量分数计,%);BD为土壤容重(g/cm3);OM为土壤有机质含量(g/kg);OC为土壤有机碳含量(g/kg);qe为土壤孔隙度;s为土壤饱和含水量;b为与粒径有关的变量;topsoil是值为1(深度0 ~ 30 cm)或0(深度>30cm)的序数变量,本研究中取1。
模型评价指标的计算:

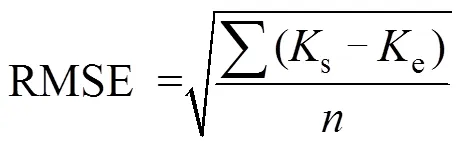
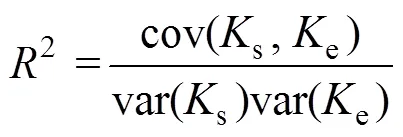
式中:s为实际测量的土壤饱和导水率(mm/min);e为模型预测的土壤饱和导水率(mm/min);为测量的数据点的数量;ME反映了估算值对实测值的平均偏离程度,ME值越接近0,模型拟合效果越好;RMSE反映估算值与实测值的吻合程度,RMSE值越小,则越接近于实测值;2反映了估算值与实测值在变化趋势上的相似性,2越接近1,说明估算值与实测值在变化趋势上越相似[39]。
2 结果与讨论
2.1 研究区土壤理化性质
研究区属于典型高山森林系统,不同土层的基本理化性质如表2所示,可见,不同土壤深度土壤理化性质变化较为明显,随土壤深度增加,容重和土壤黏粒含量逐渐增大,表层土壤容重范围介于0.69 ~ 0.98 g/cm3,这是由于森林表层土壤因根系丰富,土壤较疏松,随着土壤深度的增加,土壤结构越为紧实,导致较深层次土壤容重增加[40]。表层(0 ~ 10 cm)土壤凋落物丰富,有机质含量平均含量为46.59g/kg,平均含石率为2.77%;随土壤深度增加,含石率逐渐升高,而有机质含量逐渐降低,50 ~ 100 cm土层有机质含量仅为15.33 g/kg,而含石率增加到19.33%。从土壤颗粒组成看,砂粒是主要的粒级,占比介于77.81% ~ 97.27%,且表现出随土层深度的增加逐渐增加的趋势。变异系数可反映实测数据与平均值之间的差异性,可表示数据的离散程度,用实测数据标准差与平均值的比来表示。变异系数 <0.15属于弱变异性,0.16 ~ 0.35属于中等变异性,>0.36表示较强的变异性[41]。由表2可知,不同土层容重变异系数 <0.35,在空间变异上属于弱变异性;表层土壤有机质含量变异程度较小,深层土壤有机质变异系数>0.36,变异程度较大;土壤表层含石率变异系数为0.80,变异程度较大;全土层土壤砂粒变异系数范围介于0.02 ~ 0.07,变异程度最小。

表2 横断山地区0 ~ 100 cm土壤的基本理化性质统计特征
注:L1、L2、L3、L4分别代表 0 ~ 10、10 ~ 20、20 ~ 50、50 ~ 100 cm 土壤深度。
2.2 经典土壤饱和导水率传递函数在研究区的适用性
本文选用表1所列举的9种经典土壤传递函数,对研究区土壤s值进行估算。表3为应用9种s传递函数计算所得的估算值与实测值的RMSE、ME和2。结果发现,9种传递函数ME值均大于10,表明估算值大大低估了研究区实测s值,无法达到预测效果,Ahuja模型预测效果优于其他8种传递函数,但仍然达不到预测精度;9种传递函数RMSE值介于16.60 ~ 24.46 mm/min,预测精度均较差,Ahuja模型RMSE值最小为16.60,预测精度高于其他8种传递函数,但预测效果仍属较差。从估算值与实测值的2看,9种经典传递函数预测精度均很差,即使相对略好的Saxton模型和Ahuja模型的2值分别为0.51和0.31,仍无法实现准确预测。从图1也可以看出,Weynants、Cosby、Wosten、Campbell、Pucket、Saxton和Julià模型的估算结果均位于1∶1线底部,严重低估实测值,无法达到预测效果。Vereecken和Ahuja模型结果虽分布于1∶1线两侧,但较1∶1线偏离程度较大。
从输入变量的构成来看,Cosby、Pucket和Julià传递函数仅将土壤颗粒组成作为输入变量来估算s,适用于低海岸平原地区黏粒含量大于20% 且大孔隙不发达的土壤[32,34,37];Campbell传递函数在考虑土壤粒径分布的基础上加入容重作为输入变量,构建s传递函数,适用于美国北部土壤类型[6];Rawls等[42]指出土壤有机质含量是影响s的重要因素,Weynants、Wosten和Vereecken传递函数在考虑土壤粒径分布和容重的基础上,将有机质含量作为输入变量构建传递函数;Saxton模型则加入土壤饱和含水量作为因子;Ahuja模型是以孔隙度为唯一变量构建的模型。然而,目前以传统影响因子构建的传递函数均大大低估了本研究区土壤s。究其原因,有两个方面,其一,横断山地区高山森林生态系统植物根系发达,容易形成土壤大孔隙,为土壤优先流提供通道[43],大大改变土壤s,然而,目前经典传递函数均没有考虑土壤大孔隙对土壤s的影响;其二,由坡积物发育的研究区土壤的石砾含量高,而石砾是形成大孔隙的重要因素之一[44],因此,此类土壤大孔隙极为丰富。土壤大孔隙是影响s的重要因素,关于土壤大孔隙与s之间的关系已有大量报道,王金悦等[45]研究发现林地土壤大孔隙的总数量决定了s66% 的变异,大孔隙的平均体积决定了s79% 的变异;刘目兴等[46]发现半径 >1 mm 的大孔隙数量决定了s85%的变异。显然,大孔隙的数量与体积对土壤水分的运移与分布有着重要的影响,大孔隙的数量越多、体积越大,土壤s值越大。综上所述,本研究区植物根系发达,土壤石砾含量高,导致土壤大孔隙发达,土壤导水能力极强,故而采用传统经典传递函数会大大低估本区的s值。因此,本研究将土壤石砾含量作为新增的输入变量,考虑由石砾作用所造成的土壤优先流对土壤s的影响,从而构建适合本研究区的s传递函数,用于预测土壤s值。

表3 9种经典传递函数和新建传递函数的Ks估算值误差
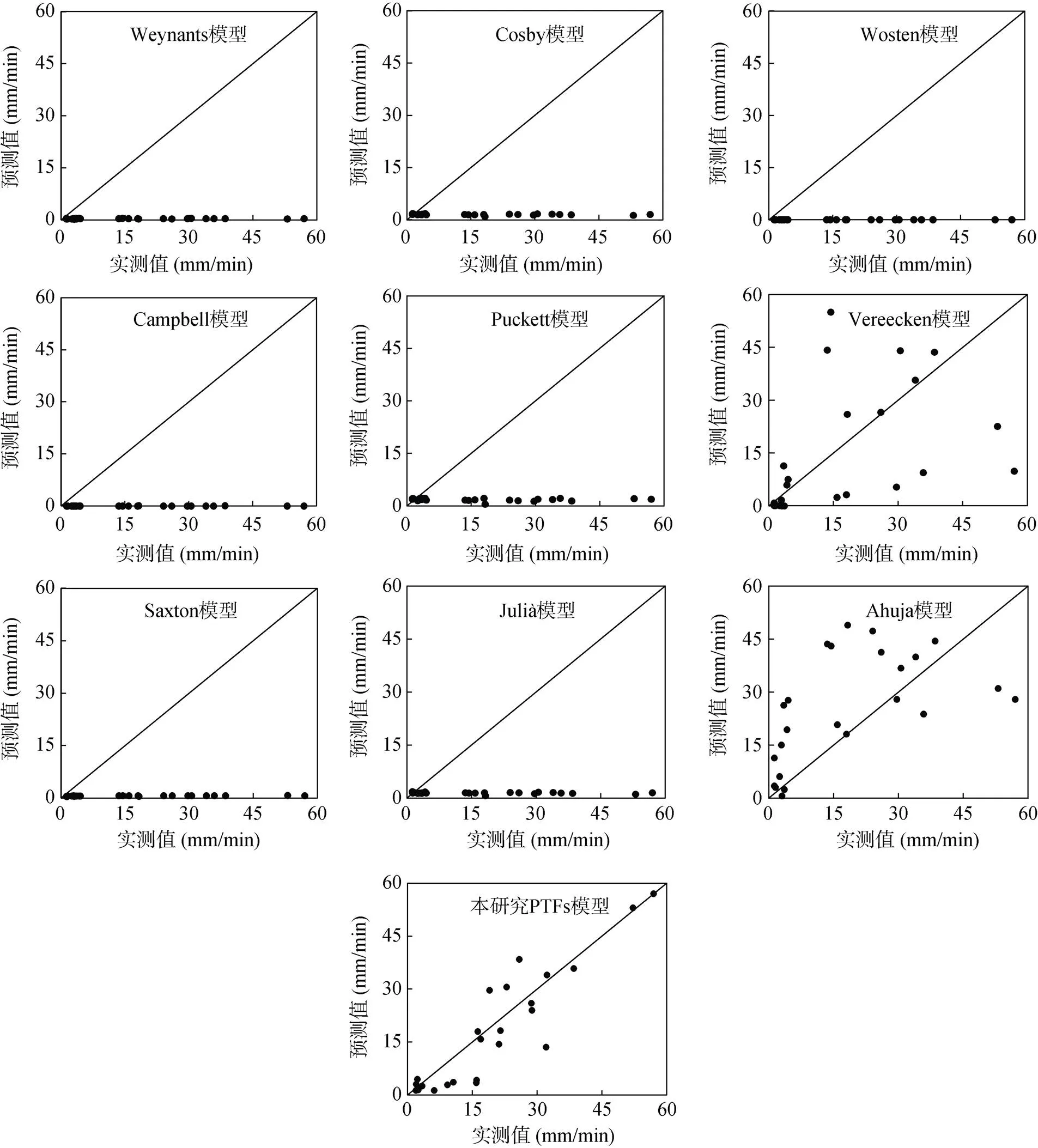
图1 不同传递函数的土壤饱和导水率估算值与实测值对比
2.3 研究区土壤饱和导水率与基本理化性质的相关性
土壤s与理化性质的相关性分析结果如图2所示,可见,s与含石率(GF)在<0.01水平下显著负相关,与容重(BD)在<0.05水平下显著负相关,表明土壤含石率和容重是影响横断山区森林土壤s的主要限制因子。s与有机质含量(SOM)、黏粒含量(clay)的相关性不大,表明横断山区土壤s受有机质含量和土壤颗粒组成影响不显著。

(图中Ks为饱和导水率;sand、silt、clay分别为土壤砂粒、粉粒和黏粒的含量;BD为土壤容重;SOM为土壤有机质含量;*、**、***分别代表在P<0.05、P<0.01、P<0.001水平显著相关)
2.4 研究区土壤饱和导水率传递函数的构建
目前,国内外s传递函数主要采用容重、有机质含量、土壤孔隙度以及土壤粒级分布作为输入变量[32-36],经验证,并不适用于横断山研究区。在石质山区,只针对土壤部分展开研究而不考虑石砾的作用是不全面的,横断山地区土壤属森林土壤,具有较高的石砾含量、发达的根系以及丰富的大孔隙,这些特点对土壤入渗、蒸发、径流等水文过程产生重要影响[47]。一方面,王慧芳等[48]的研究表明,土壤中存在的石砾有显著增加s的作用,且碎石含量越高,增幅越明显,导致传统s传递函数对含石砾土壤的适用性很差[49]。另一方面,当土壤中石砾含量较高时,石砾与土壤交界处更容易形成大孔隙,而土壤中大孔隙的数量及连通性是影响s的主要因素,当石砾含量增加到某一范围时,大孔隙之间的连通性会显著提高,形成有效的大孔隙通道,发生优先流,水分移动速度加快,s发生明显的跃升[50]。Xu等[51]等研究发现,当石砾含量 >15% 时,s随着石砾含量的增加呈现显著增加趋势。本文在研究石砾含量对s的影响时,重点关注土壤中>2 mm 的石砾[52],研究成果可为石砾含量丰富的森林土壤s研究提供帮助。针对此类林地土壤,本研究选择土壤含石率(GF)、容重(BD)、有机质含量(SOM)、黏粒含量(clay)以及粉粒含量(silt)作为初始输入变量,利用多元逐步线性回归分析法分析不同变量组合构建模型的AIC值,AIC鼓励数据拟合的优良性同时尽量避免出现过度拟合的情况。所以优先考虑的模型应该是AIC值最小的组合。由表4可知,其他变量不变的情况下,减少土壤容重作为输入变量增加模型AIC值,同时降低2;加入土壤含石率明显降低模型AIC值,同时提高模型2。选择土壤容重、含石率、黏粒含量和粉粒含量作为输入变量,构建传递函数,模型AIC值最低同时2最大,效果最佳。本研究新建的s传递函数表示为:s= 9.48 + 12.32×BD + 0.29×SOM – 1.94×GF + 2.89×silt –5.34×sand,经检验,新建传递函数ME值为5.13 mm/min,RMSE值为7.04 mm/min,预测误差明显低于9种经典传递函数,2达0.67(=40)(表3)。从图1可以看出,新建传递函数预测值和实测值分布于1∶1线两侧,预测效果较好。
杜阿朋等[53]研究表明,六盘山叠叠沟小流域森林土壤石砾中最多的是粒径在2 ~ 4 mm和 4 ~ 6 mm的破碎石砾,二者之和占总石砾体积的 62.39%,在该区研究石砾对水文的影响时应将重点放在2 ~ 6 mm 的石砾上。喻明美等[54]研究表明,环刀尺度测量s在白云山5种不同类型含石砾林地土壤具有一定的代表性。因此,充分兼顾理论和实际可操作性,本研究基于环刀尺度样品数据构建的s传递函数具有可靠性和可行性,基本适用于本研究区土壤。
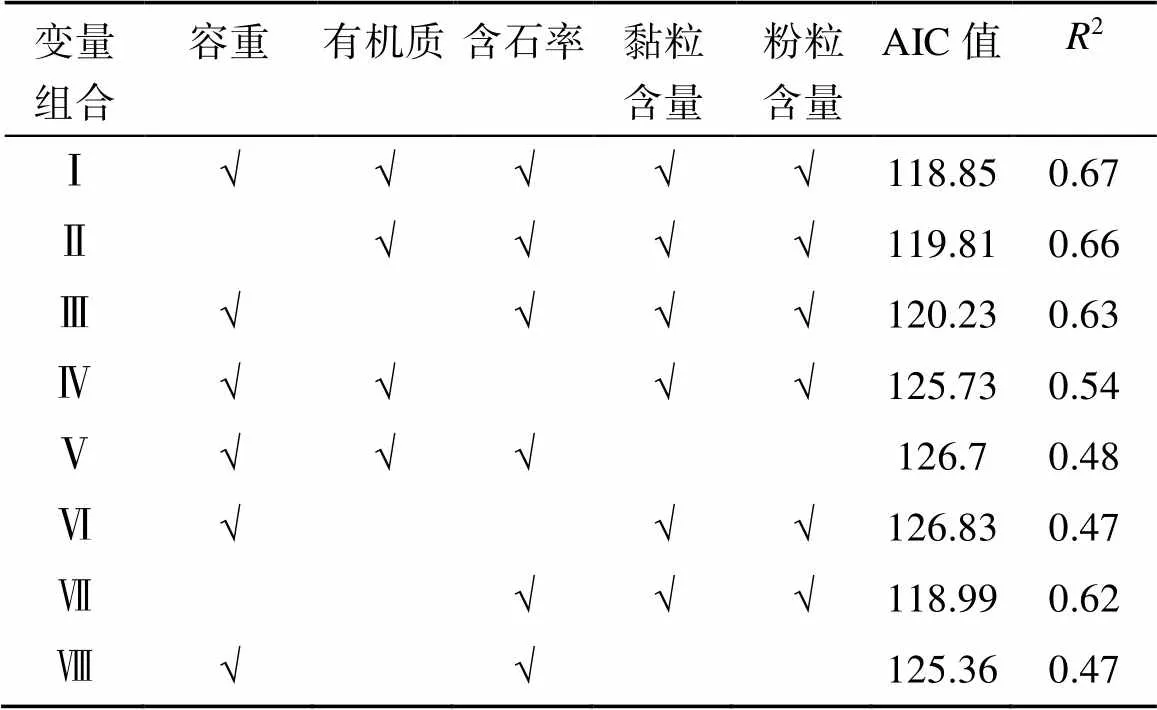
表4 土壤Ks的多元逐步线性 PTFs 回归模型及其参数检验
注:√代表选取对应参数作为模型输入变量;AIC值:赤池信息量准则,即akaike information criterion,是衡量统计模型拟合优良性的一种标准。
3 结论
研究区土壤石砾含量高,大孔隙丰富,导水能力强,表层土壤s值最高可达57.01 mm/min,经验证,现有9种经典传递函数对该区的s预测值与实测值偏差极大,不在同一个数量级上,大大低估了实测值,不适用于该区域森林土壤s预测。本研究增加土壤石砾含量(粒径 >2 mm)作为输入变量,新建传递函数:s= 9.48 + 12.32×BD + 0.29×SOM – 1.94×GF + 2.89×silt – 5.34×sand,预测值与实测值相关系数为0.67,可获得较为准确的s估算值,该模型可作为研究区s传递函数使用。
[1] Amundson R, Berhe A A, Hopmans J W, et al. Soil and human security in the 21st century[J]. Science, 2015.
[2] Bittelli M, Campbell G S, Tomei F. Soil Physics with Python[M]. New York, USA: Oxford University Press, 2015.
[3] Dai Y J, Shangguan W, Duan Q Y, et al. Development of a China dataset of soil hydraulic parameters using pedotransfer functions for land surface modeling[J]. Journal of Hydrometeorology, 2013, 14(3): 869–887.
[4] Bouma J. Using soil survey data for quantitative land evaluationadvances in soil science[A]//Stewart B A. Advances in soil science. New York: Springer, 1989: 177–213.
[5] van Looy K, Bouma J, Herbst M, et al. Pedotransfer functions in earth system science: Challenges and perspectives[J]. Reviews of Geophysics, 2017, 55(4): 1199–1256.
[6] Campbell G S, Shiozawa S. Prediction of hydraulic properties of soils using particle-size distribution and bulk density data[M]. 1992.
[7] Wang Y Q, Shao M G, Liu Z P. Pedotransfer functions for predicting soil hydraulic properties of the Chinese loess plateau[J]. Soil Science, 2012, 177(7): 424–432.
[8] Zhang Y G, Schaap M G. Weighted recalibration of the Rosetta pedotransfer model with improved estimates of hydraulic parameter distributions and summary statistics (Rosetta3)[J]. Journal of Hydrology, 2017, 547: 39–53.
[9] Jarvis N J, Zavattaro L, Rajkai K, et al. Indirect estimation of near-saturated hydraulic conductivity from readily available soil information[J]. Geoderma, 2002, 108(1/2): 1–17.
[10] Deb. Variability of hydraulic conductivity due to multiple factors[J]. American Journal of Environmental Sciences, 2012, 8(5): 489–502.
[11] Bouma J, Jongerius A, Schoonderbeek D. Calculation of saturated hydraulic conductivity of some pedal clay soils using micromorphometric data[J]. Soil Science Society of America Journal, 1979, 43(2): 261–264.
[12] Elhakeem M, Papanicolaou A N T, Wilson C G, et al. Understanding saturated hydraulic conductivity under seasonal changes in climate and land use[J]. Geoderma, 2018, 315: 75–87.
[13] Hirmas D R, Giménez D, Nemes A, et al. Climate-induced changes in continental-scale soil macroporosity may intensify water cycle[J]. Nature, 2018, 561(7721): 100–103.
[14] 聂小军, 刘淑珍, 刘海军, 等. 藏东横断山区草地利用变化对土壤质量的影响[J]. 山地学报, 2009, 27(6): 676–682.
[15] 徐瑞池, 李秀珍, 胡凯衡, 等. 横断山区山地灾害的动态危险性评价[J]. 灾害学, 2019, 34(3): 196–201, 208.
[16] 胡凯衡, 魏丽, 刘双, 等. 横断山区泥石流空间格局和激发雨量分异性研究[J]. 地理学报, 2019, 74(11): 2303–2313.
[17] 李慧霞, 刘建立, 朱安宁, 等. 预测天然文岩渠流域土壤饱和导水率的土壤转换函数方法比较研究[J]. 土壤, 2010, 42(3): 438–445.
[18] 熊东红, 翟娟, 杨丹, 等. 元谋干热河谷冲沟集水区土壤入渗性能及其影响因素[J]. 水土保持学报, 2011, 25(6): 170–175.
[19] 刘芝芹, 黄新会, 王克勤. 金沙江干热河谷不同土地利用类型土壤入渗特征及其影响因素[J]. 水土保持学报, 2014, 28(2): 57–62.
[20] 张建辉, 李勇, 杨忠. 云南元谋干热河谷造林区植被生长与土壤渗透性的关系[J]. 山地学报, 2001, 19(1): 25–28.
[21] 战海霞. 鲁中南山区不同植物群落下土壤颗粒分形与水文特征[D]. 泰安: 山东农业大学, 2009.
[22] 倪化勇. 海螺沟景区典型泥石流流域地貌特征及灾害防治[J]. 水土保持研究, 2010, 17(1): 154–158.
[23] 沈泽昊, 方精云, 刘增力, 等. 贡嘎山东坡植被垂直带谱的物种多样性格局分析[J]. 植物生态学报, 2001, 25(6): 721–732.
[24] Sun H Y, Wu Y H, Yu D, et al. Altitudinal gradient of microbial biomass phosphorus and its relationship with microbial biomass carbon, nitrogen, and rhizosphere soil phosphorus on the eastern slope of Gongga Mountain, SW China[J]. PLoS One, 2013, 8(9): e72952.
[25] 张保华, 何毓蓉, 苗国增, 等. 贡嘎山东坡亚高山林区土壤结构综合评价[J]. 山地学报, 2006, 24(4): 504–509.
[26] 何毓蓉, 张保华, 黄成敏, 等. 贡嘎山东坡林地土壤的诊断特性与系统分类[J]. 冰川冻土, 2004, 26(1): 27–32.
[27] 邵明安, 王全九, 黄明斌. 土壤物理学[M]. 北京: 高等教育出版社, 2006.
[28] 王庆礼, 代力民, 许广山. 简易森林土壤容重测定方法[J]. 生态学杂志, 1996, 15(3): 68–69.
[29] 鲁如坤. 土壤农业化学分析方法[M]. 北京: 中国农业科技出版社, 2000.
[30] 王红兰, 唐翔宇, 张维, 等. 施用生物炭对紫色土坡耕地耕层土壤水力学性质的影响[J]. 农业工程学报, 2015, 31(4): 107–112.
[31] Weynants M, Vereecken H, Javaux M. Revisiting vereecken pedotransfer functions: Introducing a closed-form hydraulic model[J]. Vadose Zone Journal, 2009, 8(1): 86–95.
[32] Cosby B J, Hornberger G M, Clapp R B, et al. A statistical exploration of the relationships of soil moisture characteristics to the physical properties of soils[J]. Water Resources Research, 1984, 20(6): 682–690.
[33] Wosten T J H M . pedotransfer functions to evaluate soil quality. 1997.
[34] Puckett W E, Dane J H, Hajek B F. Physical and mineralogical data to determine soil hydraulic properties[J]. Soil Science Society of America Journal, 1985, 49(4): 831–836.
[35] Vereecken H, Maes J, Feyen J. Estimating unsaturated hydraulic conductivity from easily measured soil properties[J]. Soil Science, 1990, 149(1): 1–12.
[36] Saxton K E, Rawls W J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions[J]. Soil Science Society of America Journal, 2006, 70(5): 1569–1578.
[37] Julià M F, Monreal T E, Jiménez A S D C, et al. Constructing a saturated hydraulic conductivity map of Spain using pedotransfer functions and spatial prediction[J]. Geoderma, 2004, 123(3/4): 257–277.
[38] Ahuja L R, Cassel D K, Bruce R R, et al. Evaluation of spatial distribution of hydraulic conductivity using effective porosity data[J]. Soil Science, 1989, 148(6): 404–411.
[39] 孙丽, 刘廷玺, 段利民, 等. 科尔沁沙丘-草甸相间地区表土饱和导水率的土壤传递函数研究[J]. 土壤学报, 2015, 52(1): 68–76.
[40] 韩光中, 王德彩, 谢贤健. 中国主要土壤类型的土壤容重传递函数研究[J]. 土壤学报, 2016, 53(1): 93–102.
[41] Yavitt J B, Harms K E, Garcia M N, et al. Spatial heterogeneity of soil chemical properties in a lowland tropical moist forest, Panama[J]. Soil Research, 2009, 47(7): 674.
[42] Rawls W J, Nemes A, Pachepsky Y. Effect of soil organic carbon on soil hydraulic properties[J]. Developments in Soil Science, 2004, 30: 95–114.
[43] 敖家坤, 牛健植, 谢宝元, 等. 土壤大孔隙结构对饱和导水率的影响[J]. 北京林业大学学报, 2021, 43(2): 102–112.
[44] 董辉, 罗潇, 李智飞. 堆积碎石土细观孔隙空间特征对其渗透特性的定量影响[J]. 中南大学学报(自然科学版), 2017, 48(5): 1367–1375.
[45] 王金悦, 邓羽松, 李典云, 等. 连栽桉树人工林土壤大孔隙特征及其对饱和导水率的影响[J]. 生态学报, 2021, 41(19): 7689–7699.
[46] 刘目兴, 吴丹, 吴四平, 等. 三峡库区森林土壤大孔隙特征及对饱和导水率的影响[J]. 生态学报, 2016, 36(11): 3189–3196.
[47] 白一茹, 赵云鹏, 王幼奇, 等. 宁夏砂田不同砾石覆盖厚度土壤入渗过程及模型分析[J]. 水土保持学报, 2017, 31(4): 81–85.
[48] 王慧芳, 邵明安, 王明玉. 小碎石与细土混合介质的导水特性[J]. 土壤学报, 2010, 47(6): 1086–1093.
[49] Nasri B, Fouché O, Torri D. Coupling published pedotransfer functions for the estimation of bulk density and saturated hydraulic conductivity in stony soils[J]. CATENA, 2015, 131: 99–108.
[50] 高鹏飞, 冉卓灵, 韩珍, 等. 含岩屑紫色土水力特性及饱和导水率传递函数研究[J]. 土壤学报, 2021, 58(1): 128–139.
[51] Xu L H, Shi Z J, Wangle Y H, et al. Contribution of rock fragments on formation of forest soil macropores in the stoney mountains of The Loess Plateau, China[J]. Journal of Food Agriculture & Environment, 2012, 10(2): 1220–1226.
[52] 张英虎, 牛健植, 李娇, 等. 石砾参数对土壤水流和溶质运移影响研究进展[J]. 土壤, 2014, 46(4): 589–598.
[53] 杜阿朋, 王彦辉, 管伟, 等. 六盘山叠叠沟小流域的土壤石砾含量坡面分布特征[J]. 水土保持学报, 2009, 23(5): 76–80, 127.
[54] 喻明美, 谢正生. 广州市白云山五种森林类型的土壤渗透性研究[J]. 水土保持研究, 2011, 18(1): 153–156.
Evaluation and Construction of Pedo-transfer Function of Saturated Hydraulic Conductivity of Forest Soils in Hengduan Mountain Region
SUN Zhixiang1,2, CUI Junfang1*, YANG Ruxing1,2, TANG Xiangyu1, WANG Genxu3
(1 Institute of Mountain Hazards and Environment, Chinese Academy of Sciences, Chengdu 610041, China; 2University of Chinese Academy of Sciences, Beijing 100049, China; 3 Key Laboratory of Hydraulics and Mountain River Development and Protection, Sichuan University, Chengdu 610207, China)
Nine classical pedo-transfer functions (PTFs) of soil saturated hydraulic conductivity(s) were used to estimatesof soils under different forests types in the Hengduan Mountains region. The results show that the estimatedsby these PTFs deviate greatly from the measured data, indicating that current PTFs models are not applicable to the soils in the Hengduan Mountains. Considering the enrichment of soil gravels in study area, a new pedo-transfer function ofsis established which containing soil gravel content (>2 mm, GF), bulk density (BD), organic matter content (SOM), and particle size distribution:s= 9.48 + 12.32×BD + 0.29×SOM – 1.94×GF + 2.89×silt – 5.34×sand. The new pedo-transfer function can better predictsof forest soils in studied area with the correlation coefficient up to 0.67, which provides a crucial parameter estimation tool for studies on forest hydrological processes and natural hazards in mountainous areas.
Forest soil; Saturated hydraulic conductivity; Pedo-transfer function; Hengduan Mountain region
S152.7
A
10.13758/j.cnki.tr.2022.03.021
孙志祥, 崔俊芳, 杨汝馨, 等. 横断山区森林土壤饱和导水率传递函数的评价与构建研究. 土壤, 2022, 54(3): 594–601.
第二次青藏高原综合科学考察研究项目(2019QZKK0903)、中国科学院战略性先导科技专项(A类)(XDA23090202)和国家自然科学基金重大项目(41790431)资助。
(jfcui@imde.ac.cn)
孙志祥(1994—),男,安徽舒城人,博士研究生,主要从事土壤水文学研究。E-mail:sunzhixiang915@163.com

