浑水含沙率对一维垂直入渗特性及致密层形成特性的影响①
钟 韵,费良军,朱士江*,何 军,康守旋
浑水含沙率对一维垂直入渗特性及致密层形成特性的影响①
钟 韵1,2,费良军3,朱士江1,2*,何 军1,2,康守旋3
(1 三峡大学三峡库区生态环境教育部工程研究中心,湖北宜昌 443002;2 三峡大学水利与环境学院,湖北宜昌 443002;3 西安理工大学省部共建西北旱区生态水利国家重点实验室,西安 710048)
水中带沙是浑水灌溉较清水灌溉的本质区别,为揭示浑水含沙率对一维垂直入渗特性及致密层形成特性的影响,通过室内一维垂直入渗试验,以清水入渗为对照,设置了4个浑水含沙率水平(3%、6%、9%、12%),研究了浑水含沙率对一维垂直入渗能力、湿润锋运移距离、致密层土壤颗粒组成及落淤层厚度等的影响,分别提出了以浑水含沙率和入渗历时为自变量的累积入渗量模型和湿润锋运移距离模型,建立了不同含沙率的浑水一维垂直入渗落淤层厚度与入渗历时之间的关系。结果表明:浑水累积入渗量、入渗率和湿润锋运移距离均随含沙率的增加而减小,而落淤层厚度随浑水含沙率的增加而增大;入渗初期(0 ~ 20 min)的落淤层厚度较小,入渗中期(20 ~ 130 min)的落淤层厚度增加较快,而其厚度增加速率逐渐变小,入渗后期的落淤层厚度稳定增加;随着浑水含沙率的增大,滞留现象越明显,落淤层细颗粒相对含量越少,粗颗粒相对含量越多;滞留层细颗粒相对含量随着含沙率的增加而增多,其物理性黏粒含量显著高于原土壤,特别是在入渗深度为0 ~ 1 cm处。
浑水含沙率;一维垂直入渗;入渗特性;致密层;土壤颗粒组成
我国黄河流域大部分区域均处在干旱半干旱地区,该地区雨量稀少而集中,水资源严重不足[1-2],且水土流失十分严重,致使黄河成为世界上含沙量最高的河流[3-4]。为解决水资源短缺问题,该地区一些灌区结合自身流域特点及生产实际,开展了引浑淤灌[5-6]。多年来,引浑淤灌的实践证明,浑水灌溉不仅缓减了该地区的旱情,而且显著提高了土壤肥力,改善土壤结构,促进作物增产提质[7-8]。浑水灌溉与清水灌溉的本质区别在于灌溉水中挟带泥沙,浑水入渗过程中泥沙颗粒易在土壤表层沉积形成致密层使得土壤结构发生变化,从而改变了水分入渗的上边界条件,影响了土壤的入渗机制[9-11],因此现有的清水入渗条件下的有关灌溉研究成果已不再适用于浑水条件下应用,浑水入渗机理亟待研究。
浑水入渗过程中致密层的形成,将土壤变成了上实下松的双层结构,其中土壤上层致密层是整个水分入渗的控制层,对水分入渗起到关键作用,即浑水灌溉条件下,土壤的入渗能力将主要受浑水泥沙致密层的影响[12]。致密层的形成包含两种性质不同的现象:一种是泥沙颗粒沉积形成落淤层,落淤层对水分入渗的影响增加了入渗介质层,延长了水分进入土体的路径;另一种是泥沙颗粒滞留形成滞留层,入渗滞留改变的是介质层内颗粒级配,使得土壤孔隙发生变化,减小了水分入渗通道[13]。关于浑水入渗的研究,目前国外相关报道较少,目前有文献报道的仅有Bouwer等[14]曾针对大池塘渗漏问题对浑水入渗规律进行了探讨,主要研究了浑水泥沙沉积中的泥沙颗粒运动状况对渗流的影响特性。国内学者对浑水入渗问题的研究重点在于落淤层对入渗的影响,没有考虑滞留层的影响,曹惠提等[15]通过一维垂直入渗试验,探讨了浑水土壤一维垂直入渗特性及其影响因素,指出浑水降低了土壤入渗能力,这主要与浑水含沙率和泥沙中物理性黏粒含量有关;费良军和王文焰[16]基于不同的已知条件和影响因素,提出了3个浑水间歇入渗模型;汪志荣等[17]提出了基于不同含沙率的浑水波涌灌入渗的Green-Ampt模型;费良军等[18]、钟韵等[19]、刘利华等[20]、张全菊等[21]对浑水膜孔灌入渗特性及影响因素进行了一系列研究,指出浑水中泥沙对土壤入渗能力影响显著。以上针对浑水入渗的研究均只简单阐述浑水入渗特性及其影响因素,而未涉及到田面地表土壤孔隙、泥沙沉积致密层形成与发展规律等方面,而浑水灌溉的入渗机制较清水更为复杂。因此,本文拟基于现有研究成果,开展浑水含沙率对一维垂直入渗特性及致密层形成特性的影响研究,以期为进一步深入探讨浑水灌溉提供理论依据。
1 材料与方法
1.1 试验材料
试验在西安理工大学西北旱区生态水利工程国家重点实验室进行,试验土样为粉砂壤土(美国制标准USDA),采自西安市灞桥区,风干碾碎后过2 mm筛,土壤初始质量含水量为0.03 kg/kg,土壤饱和质量含水量为0.37 kg/kg,物理性黏粒含量为25.06%,饱和导水率为0.017 2 cm/min,田间持水量为0.26 kg/kg,土壤颗粒组成通过Mastersizer-2000型激光粒度分析仪测定,粒径在≤0.002mm,0.002mm<≤0.05mm,0.05mm<≤2 mm分别占12.58%、74.98%、12.44%,各粒径含量为体积分数。将从黄河流域泾惠渠灌区渠底取得的泥沙风干后过1 mm筛后,通过称重法人工调配成质量含沙率分别为3%、6%、9% 和12% 的浑水,其泥沙颗粒级配组成见表1。

表1 浑水泥沙的颗粒级配组成
1.2 试验方法
浑水一维垂直入渗试验装置由两部分组成:土柱和马氏瓶。试验土柱采用内径为12 cm、高60 cm的有机玻璃制成,壁厚10 mm。试验前将土柱内壁清理干净,土样按照干容重1.40 g/cm3分层(5 cm)称重均匀装入土柱,采用夯实工具将土壤压实到预定高度后,在土壤表面覆膜,静置24 h。试验过程中通过加装有自动搅拌系统的马氏瓶调整水室水头为2.5 cm,使浑水的含沙率维持在稳定的范围。入渗结束后每隔1 cm取土30 g左右,烘干碾碎过2 mm筛后,测定各层的土壤颗粒组成。每组试验均进行3次重复,取其平均值进行结果分析。
1.3 测定项目
浑水灌溉后土壤的结构见图1所示,本文将致密层分成落淤层和滞留层两个部分来分析。

图1 浑水入渗后土壤结构示意图
1)累积入渗量:按照先密后疏的时间间隔通过马氏瓶读取。
2)湿润锋运移距离:由于所用风干土壤颜色较淡,湿润体颜色显著加深,因此,在透明有机玻璃外壁上定时描绘出不同入渗时刻所对应的湿润锋的位置及形状,试验结束后进行测量。
3)落淤层厚度:土样均匀装入试验土柱后,在透明有机玻璃土柱外壁标记上表土位置,将土柱表土处的标记作为表土“本体”和落淤层“客体”的分界线;入渗开始后,每隔5 min使用精度为0.01 mm的游标卡尺测量从表土标记处到落淤层表面的距离即为落淤层厚度,待厚度变化稳定后逐渐加大时间间隔,直至入渗结束。
4)落淤层、滞留层颗粒组成:采用Mastersizer- 2000型激光泥沙粒度仪测定。
1.4 数据处理与分析
利用统计学中均方根误差(RMSE)、偏差百分比(PBIAS)和平均绝对误差(MAE)3个指标,对计算值与试验观测值之间的符合度进行评价分析。其中,RMSE和MAE越接近0、PBIAS<±10% 时,表示计算值与试验观测值差异越小,两者吻合越好。各指标定义如下:


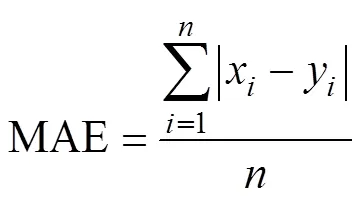
式中:x为第个观测值;y为第个计算值;为数据总个数。
2 结果与讨论
2.1 含沙率对入渗特性的影响
2.1.1 含沙率对入渗能力的影响 反映土壤入渗能力的指标为累积入渗量和入渗率。由图2、图3可以看出,不同浑水含沙率的累积入渗量随着入渗历时的延长不断增大,而入渗率则不断变小,最终趋于稳定。入渗历时相同时,累积入渗量和土壤入渗率随浑水含沙率的增加而减小。当浑水含沙率由3% 增大至12% 时,入渗结束时其累积入渗量由7.90 cm减少至4.90 cm,降幅为37.97%;相对应的稳定入渗率由0.021 6 cm/min降低至0.010 3 cm/min,降幅为52.31%,表明含沙率对浑水一维垂直入渗能力影响显著。这与文献[22-23]的研究结论类似,其中王全九等[23]将浑水泥沙对一维垂直入渗能力的减渗原因归咎于浑水泥沙对湿润锋处吸力的减小,并且研究表明湿润锋处平均吸力与浑水含沙率呈负相关关系。土壤浑水入渗特性与土壤自身特性和浑水含沙率密切相关[20, 24],浑水入渗时,泥沙颗粒逐渐在土壤表面挂淤落於,沉积在土壤表层(落淤层),并伴随着入渗水将细颗粒带入土壤孔隙中,浑水泥沙滞留减少了表层土壤的孔隙率(滞留层),形成一个密度较大的致密层[23]。这个致密层阻渗作用强,而浑水中含沙率越大,该致密层形成越快、越密实,对土壤的入渗能力影响越大。
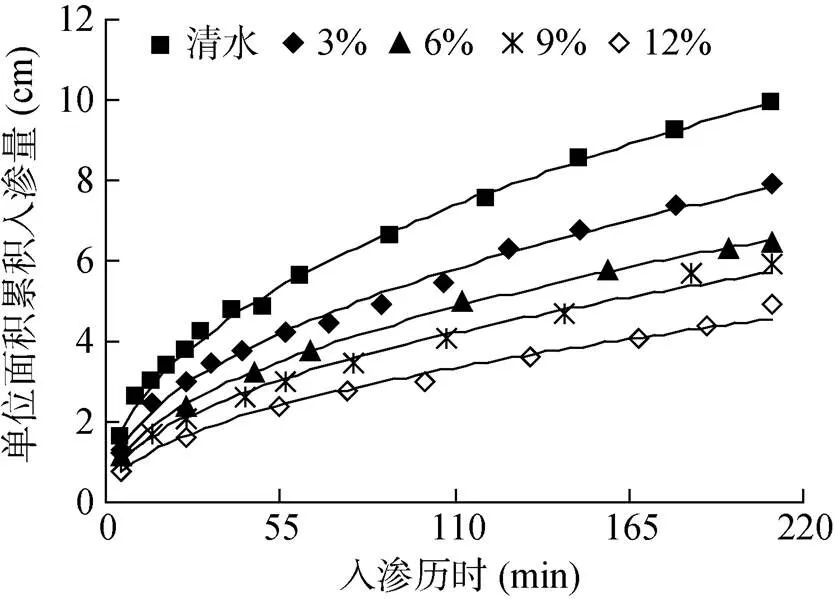
图2 一维入渗土壤累积入渗量曲线

图3 一维入渗土壤入渗率曲线
研究表明,不同浑水含沙率的累积入渗量与入渗历时的关系曲线均符合Kostiakov入渗模型。
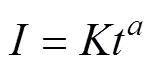
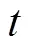
利用式(4)拟合累积入渗量与入渗历时的关系曲线结果见表2,拟合的决定系数均接近于1,表明利用Kostiakov入渗模型建立的相关关系显著。从表2可以看出,随着浑水含沙率的增大,入渗系数减小,表明随着浑水含沙率的增大,入渗开始后第一个单位时段内浑水单位面积累积入渗量减少;而入渗指数随之逐渐增大,表明随着入渗时间的延长,浑水含沙率越大,其入渗率衰减的速率较快,最终达到了稳渗阶段。研究表明,入渗系数与入渗指数随着含沙率的变化十分明显,其关系为[22, 25]:

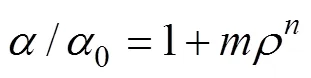
式中:0、0分别为清水的入渗系数和入渗指数;为浑水含沙率,%;、、、为拟合参数。
对表2 数据进行拟合得:


经分析,入渗系数和入渗指数与浑水含沙率关系拟合的决定系数均接近1。将式(7)和式(8)代入式(4)得到以浑水含沙率和入渗历时为自变量的浑水一维垂直入渗的累积入渗量模型,即:
0≤≤2109)
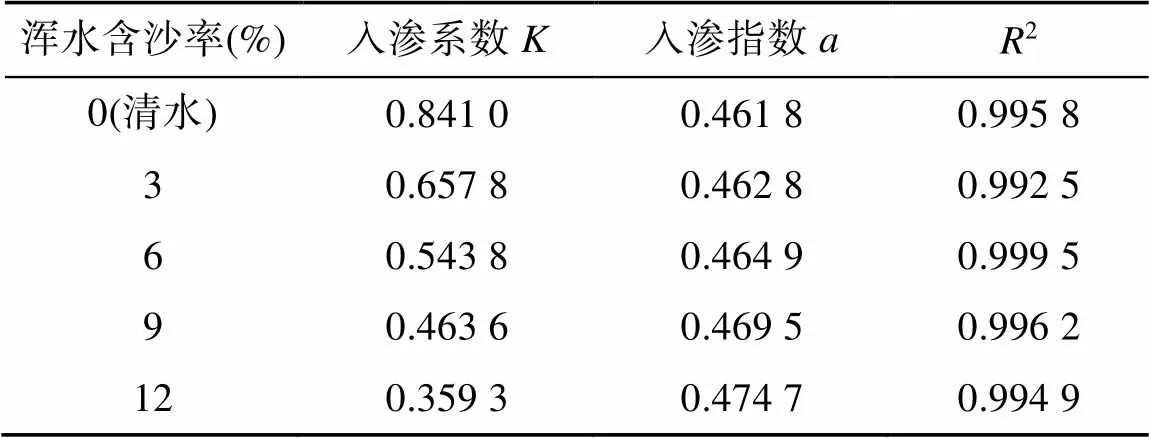
表2 不同浑水含沙率的浑水累积入渗量拟合参数
为评价该经验模型的精确度,利用相同试验条件下浑水含沙率为5% 的试验资料验证,通过式(9)计算该浑水含沙率的累积入渗量,试验实测值与模型计算值对比结果见表3。可以看出,试验实测值与模型计算值的相对误差均在±10% 以内,两者的RMSE、PBIAS和MAE分别为0.14 cm、–2.40% 和0.11 cm,RMSE和MAE都接近0,|PBIAS|<10%,表明该经验模型计算精度较高。

表3 累积入渗量实测值与计算值对比表(ρ=5%)
2.1.2 含沙率对湿润锋运移的影响 由图4可以看出,入渗历时相同时,湿润锋运移距离随浑水含沙率的增加而减小,如浑水含沙率由3%增大至12% 时,入渗结束时其湿润锋运移距离由21.15 cm减少至17.75 cm,降幅为16.08%,表明浑水含沙率对湿润锋运移距离影响显著,这与白瑞等[11]的研究结果相似。这主要是由于浑水入渗时,浑水中泥沙逐渐在土壤表面挂淤落於,形成一个密度较大的致密层,而浑水含沙率越大,该致密层形成越快越密实,对水分的阻渗作用越强,因此导致其湿润锋运移距离越小。
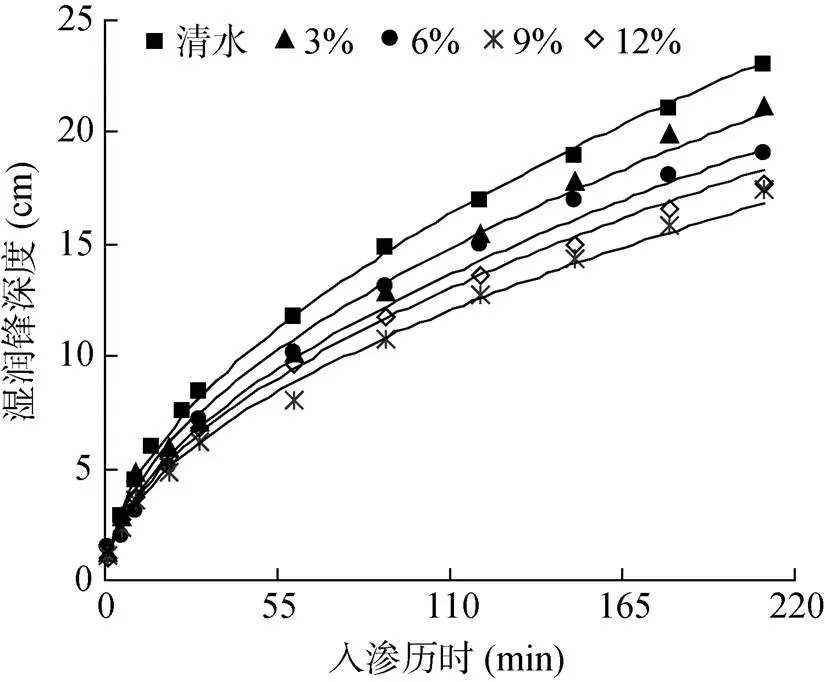
图4 一维入渗湿润锋运移曲线
经分析,浑水入渗湿润锋运移距离与入渗历时之间符合幂函数规律,即:

式中:为湿润锋运移距离(cm);为湿润锋拟合系数;为湿润锋拟合指数。
利用式(10)对图4中实测数据拟合的结果见表4。经研究表明,拟合系数、拟合指数与浑水含沙率关系为[22, 25]:
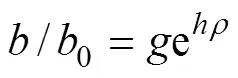

式中:0、0分别为清水入渗湿润锋的拟合系数和指数;、、、为拟合参数。
对表4 数据拟合得:
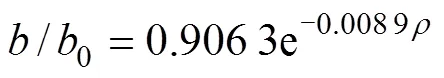
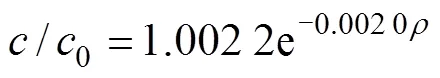
0≤≤210(15)
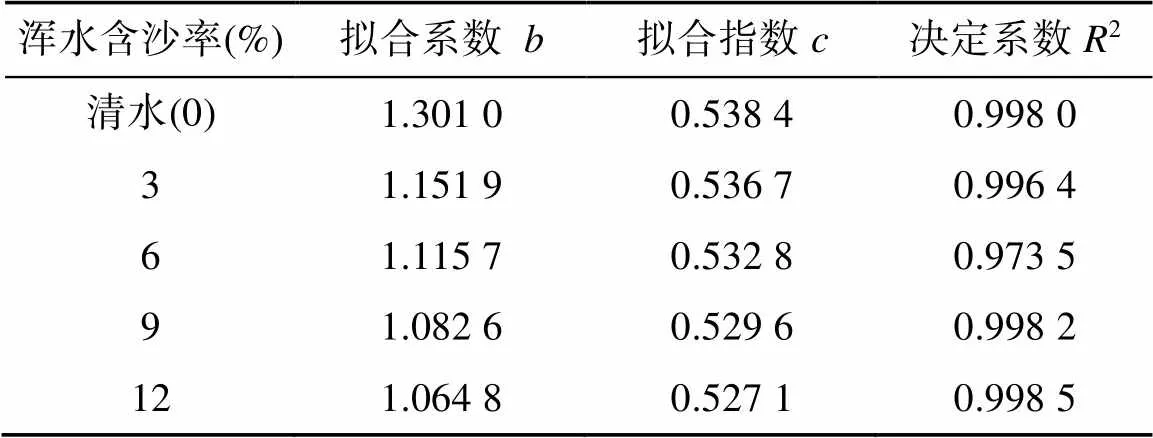
表4 不同浑水含沙率的一维垂直入渗湿润锋拟合参数
为评价该经验模型的精确度,利用相同试验条件下浑水含沙率为5% 的试验资料验证发现,试验实测值与模型计算值的相对误差均在±11% 以内,两者的RMSE、PBIAS和MAE分别为0.48 cm、–3.14%和0.39 cm,RMSE和MAE都接近0,|PBIAS|<10%,表明该经验模型计算精度较高。
2.2 含沙率对致密层形成特性的影响
2.2.1 含沙率对落淤层厚度的影响 由图5可以看出,不同含沙率对应的落淤层厚度均随入渗历时的增大而不断增大;相同入渗历时,落淤层厚度随浑水含沙率的增加而增大,入渗结束时,含沙率为3%、6%、9%、12% 的落淤层厚度分别为3.02、3.56、4.51、5.29 mm。入渗初期(0 ~ 20 min),落淤层厚度较小,这主要是由于浑水中泥沙颗粒伴随着入渗水将进入到土壤孔隙中,主要以滞留层形式进入到土壤表面,所以落淤层厚度小得无法测量。入渗中期(20 ~ 130 min)的落淤层厚度增加较快,随着入渗历时的增大,厚度增加速率逐渐变小,这是由于随着浑水累积入渗量的增加,土壤孔隙逐渐被泥沙颗粒填充,浑水中泥沙小颗粒继续洗入到土壤孔隙中,以滞留形式进入到土壤,而浑水中较大泥沙颗粒则沉积在土体表面形成落淤层,入渗过程中落淤层逐渐加厚,阻塞入渗通道,并延长了水分进入土体的路径,使得土壤导水能力变弱,进一步阻碍浑水入渗,由于浑水入渗量减小,供水速度减慢,导致落淤层厚度增加速率逐渐变小。入渗后期(130 ~ 210 min)的落淤层厚度随着入渗时间稳定增加,此时土壤表面致密层已经形成,泥沙颗粒主要以落淤层形式沉积于土壤表面,浑水入渗能力随入渗时间减小的幅度较小,所以落淤层厚度增幅也逐渐趋于基本稳定。

图5 不同浑水含沙率下落淤层厚度随入渗时间的变化曲线
研究表明,浑水一维垂直入渗落淤层厚度随入渗时间的变化曲线符合幂函数关系,根据两者的关系构造如下幂函数模型:
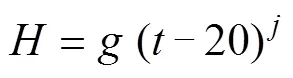
式中:为落淤层厚度(mm);、为拟合系数和拟合指数。
利用式(16)对图5中实测数据拟合的结果见表5。可以看出,拟合的决定系数均接近于1,拟合系数和拟合指数均随着浑水含沙率增大而不断增大,经分析发现拟合系数和拟合指数与浑水含沙率之间均呈线性正相关关系。


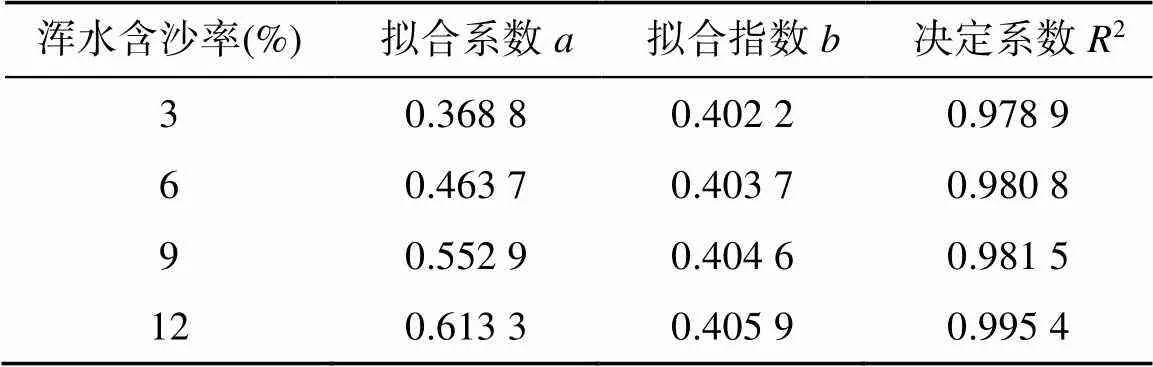
表5 不同浑水含沙率的一维垂直入渗落淤层厚度拟合参数
将式(17)和式(18)代入式(16)可得到以浑水含沙率和入渗历时为自变量的浑水一维垂直入渗的落淤层厚度计算模型,即:
0≤≤210 (19)
利用相同试验条件下浑水含沙率为5% 的试验资料对该经验模型进行验证发现,试验实测值与模型计算值两者的相对误差均在±15% 以内,两者的RMSE、PBIAS和MAE分别为0.17 mm、–6.14% 和0.15 mm,RMSE和MAE都接近0,|PBIAS|<10%,表明该经验模型计算精度较高。
2.2.2 含沙率对致密层颗粒组成的影响 由图6A的落淤层土壤颗粒组成含量曲线可知,在灌水结束时,不同浑水含沙率的落淤层中土壤细颗粒含量均低于浑水泥沙,大颗粒含量均高于浑水泥沙,表明浑水入渗过程中存在滞留现象,细颗粒进入了原土壤中,即损失了部分细颗粒的泥沙沉积在表层土壤形成落淤层。以浑水泥沙的颗粒组成为对照,含沙率为3%、6%、9%、12% 的落淤层对应的黏粒相对含量减幅依次为3.82%、25.95%、29.01% 和48.09%,表明随着浑水含沙率的增大,滞留现象越明显,落淤层细颗粒损失越多使得其相对含量越少;砂粒相对含量增幅依次为17.04%、37.53%、42.89% 和52.56%,表明随着浑水含沙率的增大,滞留现象越明显,落淤层粗颗粒相对含量越多。落淤层土壤颗粒分析结果见表6,可以看出,不同浑水含沙率的落淤层土壤物理性黏粒含量显著低于浑水泥沙,以浑水泥沙的颗粒组成为对照,浑水含沙率3%、6%、9%、12% 的落淤层对应的物理性黏粒含量0.01减幅依次为16.72%、42.55%、46.30% 和61.50%,表明浑水中泥沙含量越大,细颗粒伴随着入渗水洗入到土体的越多,其沉积在土壤表面形成落淤层的相对含量越少。

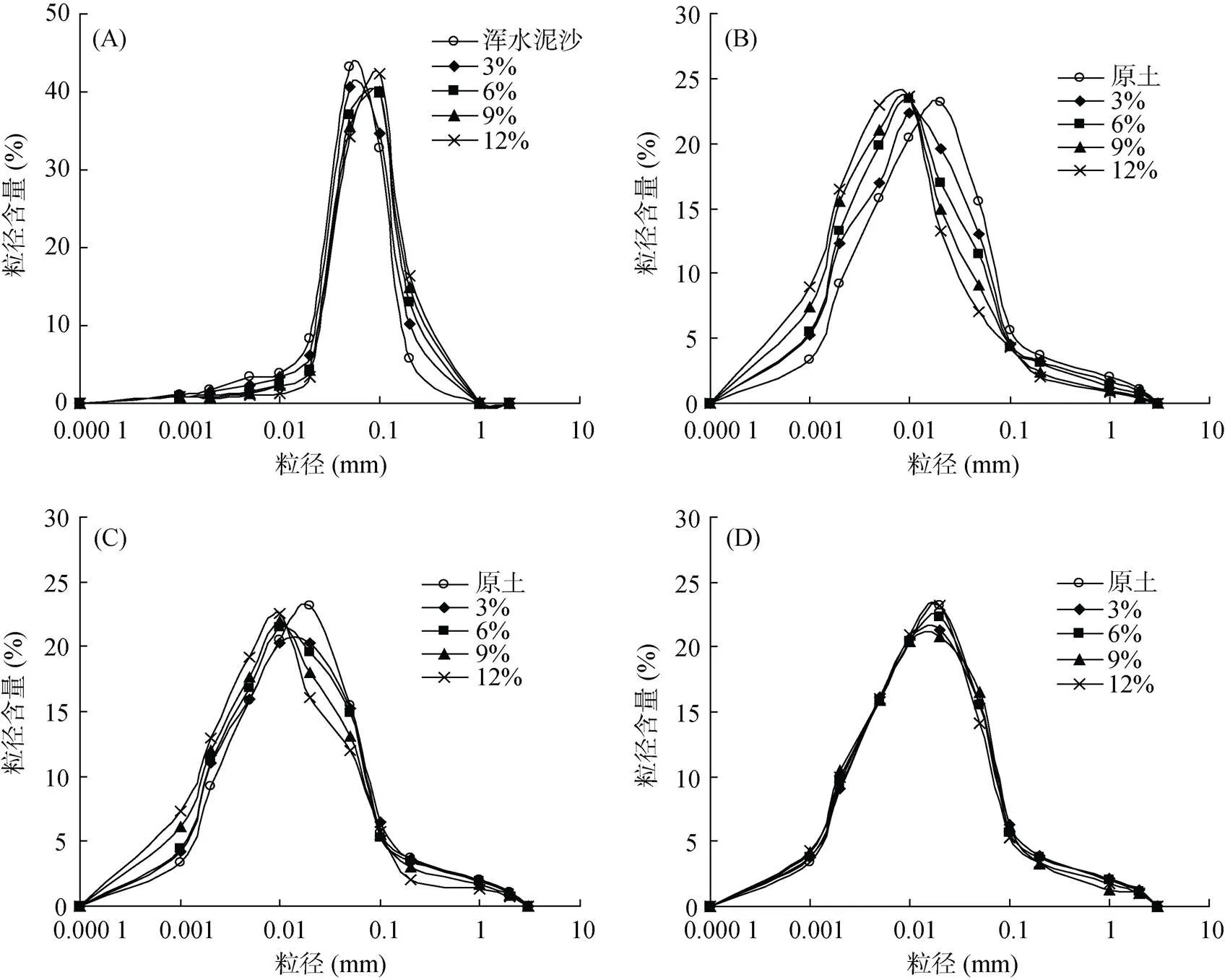
(A. 落游层;B. 滞留层0~1 cm;C. 滞留层1~2 cm;D. 滞留层1~3 cm)

表6 入渗结束后不同浑水含沙率的入渗致密层土壤颗粒分析结果
注:0.01表示泥沙颗粒级配中小于0.01 mm的粒径体积含量,其是浑水泥沙颗粒中十分活跃的部分,其含量直接影响浑水入渗规律。表中同列数据小写字母不同表示差异达<0.05显著水平,下表同。
3 结论
1)浑水累积入渗量和入渗率随含沙率的增加而减小,不同含沙率下的累积入渗量与入渗历时的关系均符合Kostiakov模型,其中入渗系数与含沙率呈幂函数负相关关系,入渗指数与含沙率呈幂函数正相关关系。
2)湿润锋运移距离随浑水含沙率的增加而减小,不同含沙率下的湿润锋运移距离与入渗历时之间符合幂函数关系,其中拟合系数和拟合指数与含沙率均呈指数函数负相关关系。
3)不同浑水含沙率对应的落淤层厚度均随入渗历时的增大而不断增大,两者符合幂函数关系,拟合系数和拟合参数均随着含沙率增大而不断增大,两者与含沙率之间均呈线性正相关关系;相同入渗历时,落淤层厚度随浑水含沙率的增加而增大。
4)随着浑水含沙率的增大,滞留现象越明显,落淤层细颗粒相对含量越少,物理性黏粒含量均显著低于浑水泥沙,粗颗粒相对含量越多;滞留层细颗粒相对含量随着含沙率的增加而增多,其物理性黏粒含量显著高于原土壤,特别是在入渗深度为0 ~ 1 cm处。
[1] Song Z W, Zhang H L, Snyder R L, et al. Distribution and trends in reference evapotranspiration in the North China plain[J]. Journal of Irrigation and Drainage Engineering, 2010, 136(4): 240–247.
[2] 李昌峰, 高俊峰, 曹慧. 土地利用变化对水资源影响研究的现状和趋势[J]. 土壤, 2002, 34(4): 191–196, 205.
[3] 夏星辉, 王君峰, 张翎, 等. 黄河泥沙对氮迁移转化的影响及环境效应[J]. 水利学报, 2020, 51(9): 1138–1148.
[4] 陈同德, 焦菊英, 王颢霖, 等. 青藏高原土壤侵蚀研究进展[J]. 土壤学报, 2020, 57(3): 547–564.
[5] 侯鹏, 肖洋, 吴乃阳, 等. 黄河水滴灌系统灌水器结构-泥沙淤积-堵塞行为的相关关系研究[J]. 水利学报, 2020, 51(11): 1372–1382.
[6] Liu L H, Fei L J, Chen L, et al. Effects of initial soil moisture content on soil water and nitrogen transport under muddy water film hole infiltration[J]. International Journal of Agricultural and Biological Engineering, 2021, 14(3): 182–189.
[7] 王锦辉, 费良军, 聂卫波. 浑水灌溉入渗特性研究进展与展望[J]. 干旱地区农业研究, 2016, 34(2): 265–270.
[8] 卞艳丽, 曹惠提, 张会敏, 等. 浑水灌溉下泥沙级配对土壤水入渗影响的试验研究[J]. 节水灌溉, 2018(11): 39–47, 50.
[9] Liu L H, Fei L J, Zhu H Y, et al. Study on the influence of fertilizer solution concentration on soil water and nitrogen transport characteristics under film hole irrigation[J]. Journal of Soil Science and Plant Nutrition, 2021, 21(2): 1653–1665.
[10] 姚雷. 浑水入渗滞留试验研究[D]. 北京: 清华大学, 2004.
[11] 白瑞, 费良军, 陈琳, 等. 含沙率对层状土浑水膜孔灌单点源自由入渗特性的影响[J]. 水土保持学报, 2020, 34(2): 43–49, 55.
[12] 纪亚男. 山东引黄灌区不同灌水定额对田间泥沙入渗规律的影响机理研究[D]. 泰安: 山东农业大学, 2015.
[13] 姚雷, 马吉明, 任理. 浑水入渗的滞留物分布特征及影响因素分析[J]. 水力发电, 2004, 30(11): 20–23.
[14] Bouwer H, Ludke J, Rice R C. Sealing pond bottoms with muddy water[J]. Ecological Engineering, 2001, 18(2): 233–238.
[15] 曹惠提, 卞艳丽, 黄福贵. 浑水灌溉下土壤水分入渗规律研究综述[J]. 人民黄河, 2010, 32(3): 69–70, 73.
[16] 费良军, 王文焰. 浑水间歇入渗模型研究[J]. 水利学报, 1999, 30(2): 39–42.
[17] 汪志荣, 王文焰, 王全九, 等. 浑水波涌灌溉入渗机制及其Green-Ampt模型[J]. 水利学报, 1998, 29(10): 44–48.
[18] 费良军, 王锦辉, 金世杰. 不同膜孔直径的浑水膜孔灌自由入渗特性研究[J]. 农业机械学报, 2016, 47(2): 172–178.
[19] 钟韵, 费良军, 傅渝亮, 等. 土壤容重对浑水膜孔灌单点源自由入渗特性的影响[J]. 水土保持学报, 2016, 30(2): 88–91, 96.
[20] 刘利华, 费良军, 陈琳, 等. 浑水含沙率对膜孔灌肥液入渗土壤水氮运移特性的影响[J]. 农业工程学报, 2020, 36(2): 120–129.
[21] 张全菊, 费良军, 刘利华, 等. 多因素影响下浑水膜孔肥液入渗土壤水分运移特性[J]. 水土保持学报, 2021, 35(1): 265–270.
[22] 王文焰, 张建丰, 王全九, 等. 黄土浑水入渗能力的试验研究[J]. 水土保持学报, 1994, 8(1): 59–62.
[23] 王全九, 王文焰, 邵明安, 等. 浑水入渗机制及模拟模型研究[J]. 农业工程学报, 1999, 15(1): 135–138.
[24] Selim T, Bouksila F, Berndtsson R, et al. Soil water and salinity distribution under different treatments of drip irrigation[J]. Soil Science Society of America Journal, 2013, 77(4): 1144–1156.
[25] 费良军. 浑水波涌灌理论与技术要素试验研究[D]. 西安: 西安理工大学, 1997.
Effect of Sediment Concentration of Muddy Water on One-dimensional Vertical Infiltration Characteristics and Dense Layer Formation Characteristics
ZHONG Yun1,2, FEI Liangjun3, ZHU Shijiang1,2*, HE Jun1,2, KANG Shouxuan3
(1 Engineering Research Center of Eco-environment in Three Gorges Reservoir Region, Ministry of Education, China Three Gorges University, Yichang, Hubei 443002, China; 2 Water Conservancy and Environmental Sciences, China Three Gorges University, Yichang, Hubei 443002, China; 3 State Key Laboratory of Eco-hydraulics in Northwest Arid Region, Xi’an University of Technology, Xi’an 710048, China)
Sediment in water is the essential difference between the irrigation of muddy and clean water. The one-dimensional vertical infiltration experiment with muddy and clean water was conducted to reveal the influence of sediment concentration in muddy water on one-dimensional vertical infiltration characteristics and dense layer formation. Four sediment concentrations (3%, 6%, 9%, 12%) were set up to study the effects of sediment concentration on one-dimensional vertical infiltration capacity, wetting front movement distance, soil particle composition in dense layer and the thickness of deposition layer. The models of cumulative infiltration and the wet front movement distance with sediment concentration in muddy water and infiltration duration as independent variables were proposed respectively, and the relationship between the thickness of deposition layer and the infiltration duration of one-dimensional vertical infiltration of muddy water with different sediment concentrations were established. The results showed that the increase of sediment concentration in muddy water, the cumulative infiltration, the infiltration rate and the movement distance of wetting front of muddy water all decreased, while the thickness of deposition layer increased. The thickness of the deposition layer was small at the initial stage of infiltration (0-20 min), increased rapidly in the middle stage of infiltration (20-130 min) but the increasing rate gradually decreased, and increased steadily in the late infiltration stage.With the increases of sediment concentration in muddy water, the sediment retention became more obvious, so the fine particles decreased while the coarse particles increased in the deposition layer. The fine particles increased in the stranded layer with the increase of sediment concentration, and the physical clay particles was significantly higher than that of the original soil, especially at 0-1 cm infiltration depth.
Sediment concentration of muddy water; One-dimensional vertical infiltration; Infiltration characteristics; Dense layer; Soil particle composition
S275.3
A
10.13758/j.cnki.tr.2022.03.022
钟韵, 费良军, 朱士江, 等. 浑水含沙率对一维垂直入渗特性及致密层形成特性的影响. 土壤, 2022, 54(3): 602–609.
国家自然科学基金项目(52079105、52000120)和湖北省水利重点科研项目(HBSLKY201919)资助。
(784471206@qq.com)
钟韵(1992—),男,江西宜春人,博士,讲师,主要从事节水灌溉研究。E-mail: zhongyunjx92@163.com

