TM-CFAR的适用场景分析和实现方式对比

游英杰 杜 力 陈颖哲 杨 刚 胡 迪

(1.西安电子工程研究所 西安 710100；2.中国人民解放军32382部队 北京 100071)

0 引言

针对目标分布和杂波的不同特性，采取适合的雷达恒虚警方法可以获得更优的检测性能。从理论分析的角度看，可以选取的方法很多，基于单元平均cfar和有序统计cfar方法，又提出了OSGO-CFAR、OSSO-CFAR等方法，但是目前工程实践中最常用的方法仍然是经典的单元平均选大GO-CFAR。一方面是在很多情况下，实际环境满足单元平均CFAR所需的基本条件：目标保持独立，即目标分布在不同的参考窗内且参考窗的干扰数据是均匀的；另一方面是GO-CFAR在DSP实现中具有很大的时间优势。而当实际环境不满足GO-CFAR的使用条件时，比如：当一个目标横跨多个距离单元，或者当杂波发生突变时。如果仍然采用GO-CFAR，会引起检测性能的急剧下降。针对这些情况，采用OS-CFAR等方法，能够在一定程度上提升检测性能，对于资源比较充足的硬件平台，采用TM-CFAR能够在OS-CFAR的基础上进一步减少cfar损失，同时还能解决OS-CFAR在杂波边缘虚警率较高的问题。本文构造了地杂波边缘场景和多目标场景，通过Matlab仿真分析GO-CFAR、OS-CFAR及TM-CFAR的检测性能，针对当前TM-CFAR常用的排序方法，给出了效率更高的实现方式，统计各种实现方法的运算时间，为工程应用提供了思路。

1 三种CFAR数学模型和分析

GO-CFAR是单元平均选大恒虚警处理技术，具体做法如下:以检测单元为中心，分为前后两个参考窗，每个参考窗内有个数据，在检测单元和参考窗之间还可以添加个保护单元。对前后两个参考窗内的数据进行平均处理，以较大的那个作为对干扰功率的估计值，将该值乘以门限系数得到检测门限，再与检测单元进行比较，检测单元过门限则认为当前值为目标。GO-CFAR的阈值因子是以下方程(1)的解为

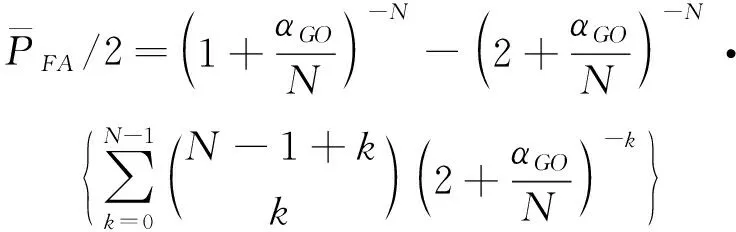
(1)

OS-CFAR是有序统计恒虚警处理技术，将检测单元前后两个参考窗内的数据合并，然后进行排序，得到一个升序排列的序列。从排完序的序列中选第个值作为对干扰功率的估计值，将该值乘以某个因子得到阈值并与检测单元进行比较，判断检测单元的值是否大于阈值，大于则认为当前检测单元为目标。OS-CFAR的阈值因子为

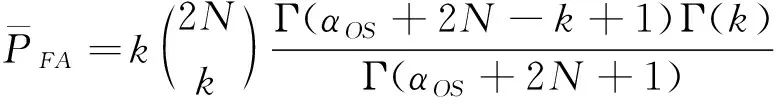
(2)

对于整数自变量，Γ()=(-1)!。当为整数时，可以化简为

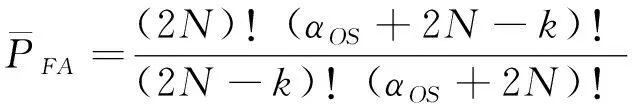
(3)

TM-CFAR也叫剔除平均CFAR，它与OS-CFAR类似，直接将两个参考窗内的数据合为一个序列，经过排序或者直接选出其中拥有最小功率值的个数据单元，以及拥有最大功率值的个数据单元并进行舍弃，对剩下的元素取平均得到对干扰功率的估计值，将估计值乘以门限系数得到检测门限，通过比较检测单元与门限值的大小判断检测单元是否包含目标。在实际应用中，优先考虑拥有最大功率值的目标，本文中将最小功率值的目标个数设为0。数学模型如图1所示。

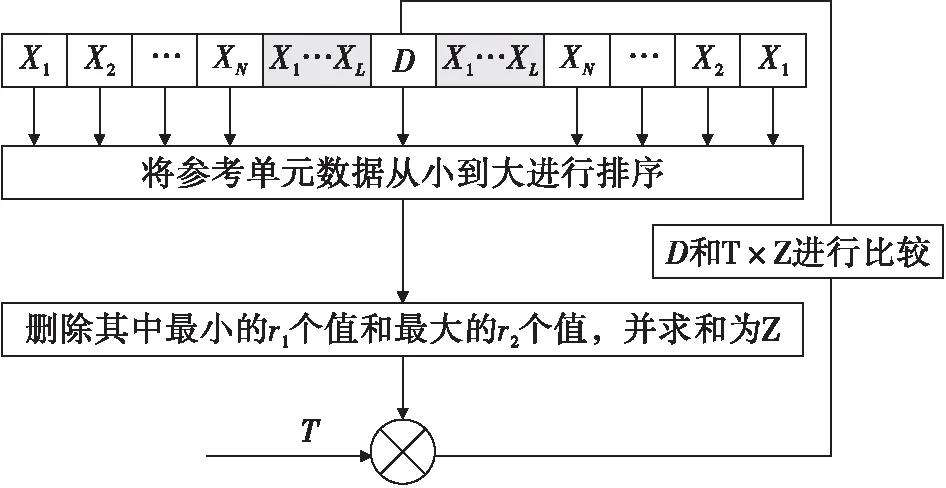
图1 TM_CFAR算法模型

检测单元杂波功率强度的估值的取值为

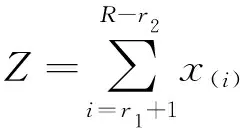
(4)

虚警概率为

(5)

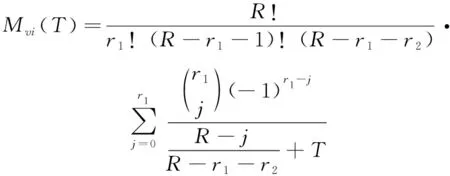
(6)

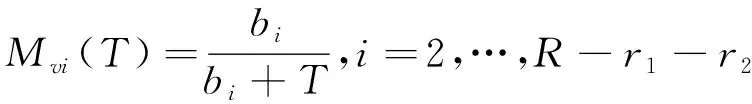
(7)

=(--+1)(---+1)

(8)

2 三种算法在不同场景下性能比较

门限因子的取值与干扰功率和虚警概率有关，在这里取虚警概率为10，并构造相同的杂波环境。具体仿真条件如下：距离单元取0～200，在0～100距离范围内生成20dB的杂波，100～200距离范围内生成30dB的杂波，杂波在前后不同的距离段符合均匀随机分布特性。在距离单元44处设置15dB的目标，在距离单元47和105处设置8dB的目标，在距离单元52和92处设置12dB的目标。参考单元的数量为36个，保护单元的数量为2个，OS-cfar选取的值为20，仿真结果如图2至图4所示。

图2 GO-CFAR检测效果图

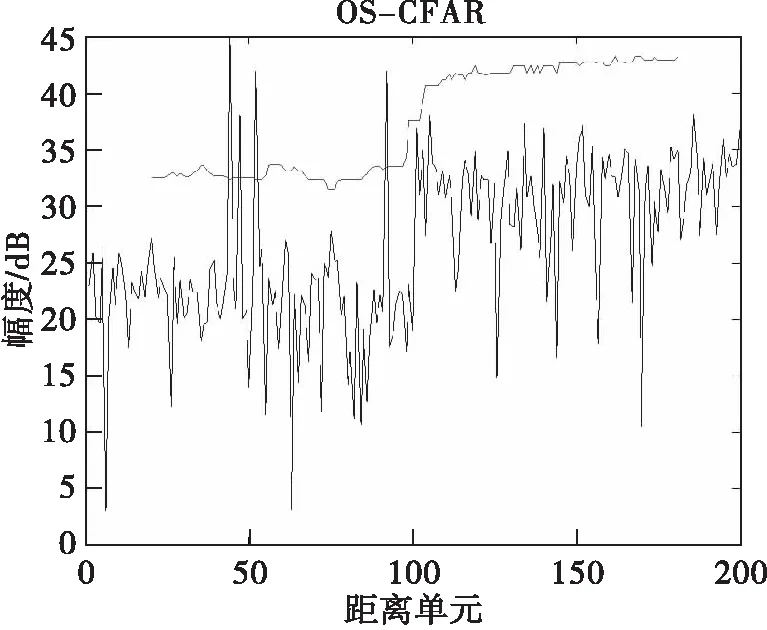
图3 OS-CFAR检测效果图

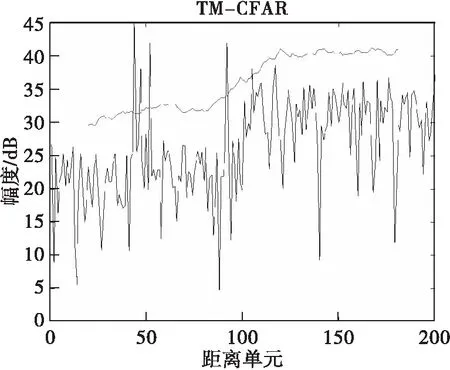
图4 TM-CFAR检测效果图

从图2可以看出，GO-CFAR对于强目标后相邻的两个弱目标都无法检测出来，存在比较严重的目标遮蔽效应，在杂波突变后，杂波边缘处的弱目标也没有检测出来。图3中，OS-CFAR能够检测出强目标后连续的两个弱目标，但是杂波边缘处存在漏警，当减小值后，有可能检测出目标，但是会提升虚警的概率，从实际应用的角度看，需要保证被干扰目标污染的参考单元数不能大于-个，而且对于值的选取存在很大的不确定性。图4中，TM-CFAR既能够检测出连续的3个强度不一的目标，对于杂波边缘处的弱目标也具有比较好的检测效果，剔除的最大功率数据单元数目可以从/4-/2之间选取，而且可以根据干扰的先验信息，比如干扰单元的数目，做出更加合理的选择。因此，TM-CFAR在某些场景下具有优于OS-CFAR的性能，对TM-CFAR的DSP实现进行研究具有一定的实用价值。TM-CFAR减小了由于目标遮蔽效应引入的CFAR损失，并在某种程度上避免了杂波边缘处理性能的降低，但是在实现过程中需要类似排序的操作，比GO-CFAR和OS-CFAR使用的时间要长。

3 TM-CFAR在DSP中的实现

本文中选用的DSP芯片是FT-M6678，这是一款高性能军用多核浮点DSP，与TI公司的TMS320C678指令集兼容。TM-CFAR的关键在于求出参考窗中前大的数据，如果采用排序的方法，每次都要对所有的参考单元进行排序，存在冗余过程。因此在这里只是运用排序的思想，用尽可能少的步骤求出结果，下面对本文选用的四种从个数中求取前大数的方法进行介绍。

3.1 运用固定数组的思想

从数组的前个数中选出最小值，用最小值和原数组第+1个数进行比较，如果大于，将放入的位置，并再次从数组的前个数中选出最小值，用最小值和第+2个数进行比较，直到数组中的最后一个元素。

3.2 运用选择排序和交换排序的思想

先将数组遍历一次，找到最大值，并将其与数组中第最后一个数进行交换。接着将数组再遍历一次，这一次只需要遍历到第-1个数，求出-1个数中的最大值。循环上述过程次，则数组中的最后个数是前大数。这种方法是一种原地运算的方法，不额外占用空间。

3.3 运用快速排序的思想

假设个数存储在数组中，选取数组中的第一个元素，把数组分为两部分和。中的元素大于等于，中的元素小于。这时有两种可能性：一种可能性是中元素的个数小于，中所有的数和中最大的-||个元素(||指中元素的个数)就是数组中最大的个数。第二种可能性是中元素的个数大于或等于，则需要返回中最大的个元素，分到元素个数较少的数组中。这样递归下去，不断把问题分解成更小的问题，平均时间复杂度为(·log2)。在具体实现的过程中，数组中第一个元素的选取要满足一定的随机性，否则有可能导致分组失败，本文引入了随机数对当前数组元素个数取余的算法，得到一个数组中的随机位置，并将随机位置上的数与第一个数进行交换。

3.4 运用堆排序的思想

首先用数组的前个数，构建一个容量为的最小堆。最小堆的堆顶元素就是当前个数中的最小的一个。然后从第+1个数开始，每次新考虑一个数，如果比堆顶的元素小，则不需要改变原来的堆。如果比堆顶的元素大，那么用替换堆顶的元素。在替换堆顶的元素之后，可能破坏最小堆的结构，需要更新堆来维持堆的性质。更新过程花费的时间为(2)，完成前大数求取需要更新的最多次数为-次。

4 TM-CFAR不同实现方法的性能比较

为了验证TM-CFAR各种实现方法的正确与否和性能优劣。先仿真雷达检测的流程，选用16个脉冲，带宽为2×10Hz，脉冲宽度为42×10s，脉冲重复周期为2.56×10s，采样率为4×10，距离点数计算得1024，目标个数设置为3个，速度分别为100m/s，150m/s，230m/s，距离分别为5000m，6300m，24000m，杂波模拟为均匀的地杂波。经过脉压，MTD和TM-CFAR检测之后的结果如图5所示。从图5中可以看出，正确的检测出了3个目标。以该仿真过程中的MTD结果作为输入，在DSP中进行检测，在验证结果正确的情况下，对各种算法检测所需时间进行记录。实际工程运用中，通过开-O3优化DSP程序可以大幅提升程序性能。图6为未开-O3优化的情况下，各种算法的运行时间随TM-CFAR剔除点数的变化情况。

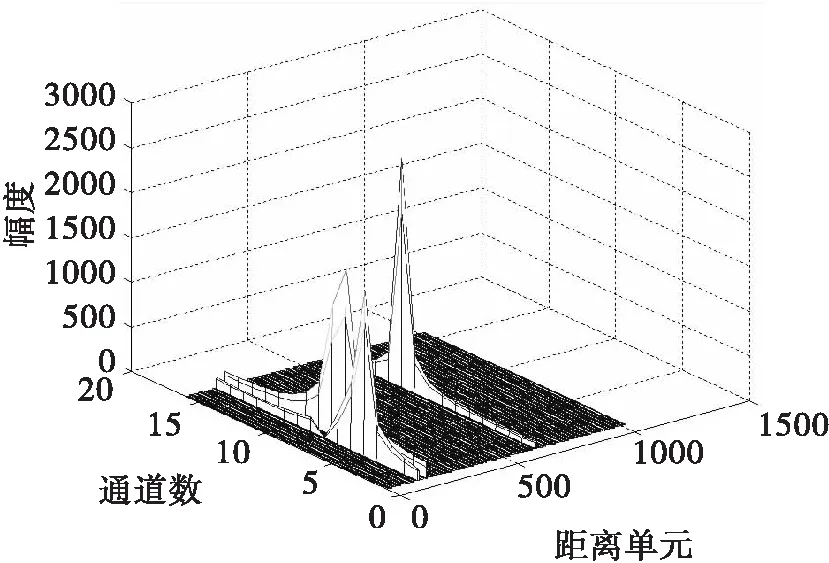
图5 TM-CFAR检测结果

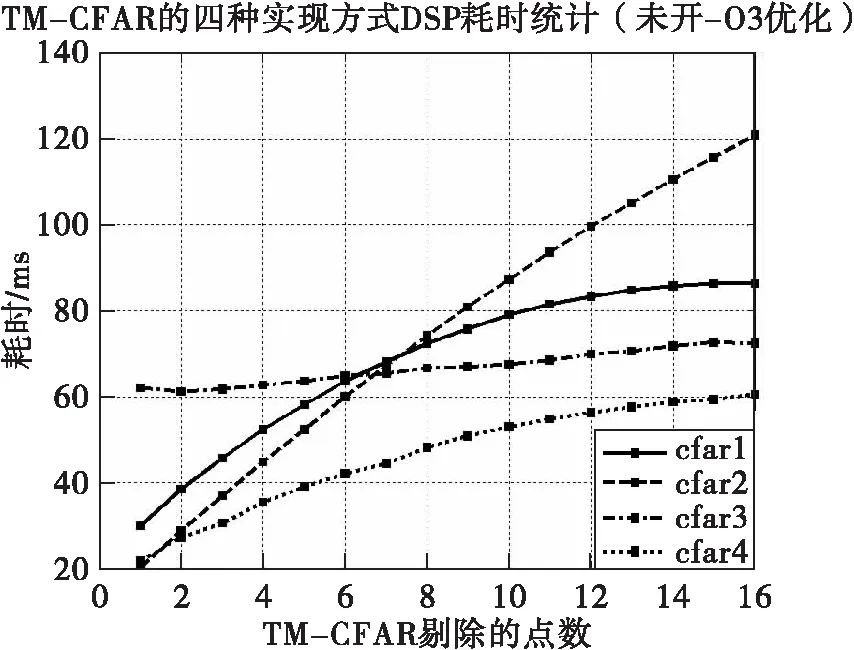
图6 未开-O3优化的情况下，不同实现方式所花费时间

从图6可以看出，在不开-O3优化时，采用cfar4即堆排序思想的实现方式具有很明显的优势，且随着剔除点数的增加，时间呈对数增长，增长较缓。采用cfar2即选择排序思想和cfar1即固定数组思想的方法在8个点之前，前者具有一定优势，但在8个点之后，前者呈线性增长，效率明显比后者低。采用cfar3即快速排序思想的方法所需时间随剔除点数的增加缓慢增长，在观测范围内基本稳定在60～70ms之间，这个时间比堆排序思想的最长时间还要长。在开-O3优化后，由于不同方法的可优化空间不同，结果与图6差别很大，具体时间统计情况如图7所示。

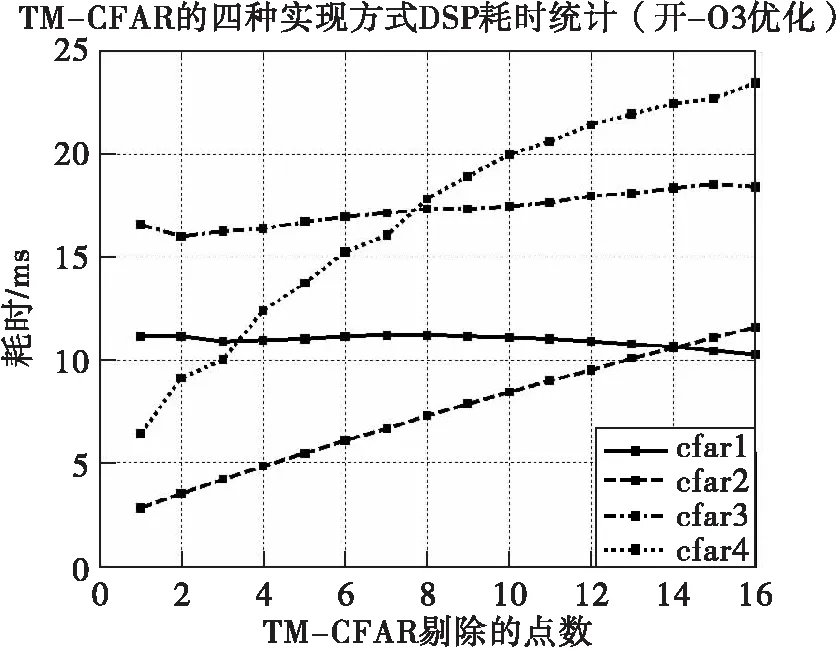
图7 开-O3优化的情况下，不同实现方式所花费时间

从图7可以看出，之前表现好的cfar4方法性能不再优越，cfar3方法耗时也很不理想。在大多数情况下cfar2方法所消耗时间相比其他算法有明显优势，只有在剔除点数大于14的情况下，cfar1比cfar2稍好一些。

再来分析一下实现TM-CFAR的四种算法在优化前后迥异表现的原因。在不指定优化标识的情况下，编译产生的代码之间指令是独立的，最明显的特点就是这个时候可以通过断点追踪程序执行的每一步。O3优化是采用-opt_level方法的最高级别的优化，这种优化会在保证变换之后的程序与源程序语义等价的情况下提升运行的速度，也就是说优化之后程序的结构会改变。具体采用的方法包括如下几种：

1)消除没有用到的分配及共用的表达式；

2)使用流水线技术对循环进行优化；

3)允许将循环进行拆分；

4)将循环中使用的数组改为指针形式；

5)将小规模的函数调用改为内联的形式等等。经过优化之后，程序运行的速度加快，但是程序结构发生变化。也正因为如此，虽然堆排序思想和快排思想在算法设计层面具有较低的时间复杂度，但是经过优化之后，这两种算法的可提升空间没有另外两种算法大，出现了运行效率不如简单算法的情况。

作为纵向对比实验，相同规模数据也做了GO-CFAR和OS-CFAR的检测处理,均采用快速算法且用O3优化后，所用时间分别为490μs和1.8ms，可以看出：GO-CFAR所用时间最短，OS-CFAR所用时间为GO-CFAR的4倍左右，TM-CFAR为OS-CFAR所用时间的2～5倍左右，当剔除点数较少时TM-CFAR与OS-CFAR效率相当，但是对于资源相对充足的处理器，都能够满足CFAR运算实时性的要求。

5 结束语

TM-CFAR在均匀杂波背景中具有良好的检测性能，在杂波边缘的虚警控制能力强于OS-CFAR，还可以根据干扰的先验信息灵活地选择合适的剔除数目。所以在目标遮蔽和杂波突变的环境中，当GO-CFAR和OS-CFAR表现不佳时，可以考虑采用TM-CFAR。本文中提出的TM-CFAR的实现方法，不需要对全部的检测单元进行排序，可以提升运行效率，满足CFAR运算实时性的要求。