基于改进型2SFCA 的梅州城区公园绿地与人口耦合度的分析
陈志云,蔡润鹏,谢作轮
(嘉应学院 地理科学与旅游学院,广东 梅州 514015)
0 前言
随着城市化进程加快,居民生活水平不断提高,其对公共绿色空间的需求愈发强烈.公园绿地作为绿色休闲空间的一部分可为居民提供休闲游憩、运动健身、舒缓身心的场所[1],也兼有减轻城市热岛效应、健全生态、美化景观等功能[2].公园绿地的数量及质量可作为一项衡量城市环境和居民生活质量的指标[3].常用的城市公园绿地建设指标有人均公园绿地面积、公园数量等,此类指标能够较好地显示城市间的差异,但反映其空间布局的合理性和居民到达公园绿地所耗成本的差异性.因此城市内部的公园绿地供给应与需求相互适应[4].
可达性(accessibility)是指从源地克服各种阻力到达目的地的相对或绝对难易程度,其指标有距离、时间、费用等[5].城市公园绿地的可达性受多种因素的影响,如公园绿地的吸引力、公园绿地的空间布局、人口分布情况等.可达性定量分析方法有缓冲区 分析法[6]、统计指标法[7]、费用加权距离法[8]、网络分析法[9]、引力模型法[10]以及两步移动搜索法[11]等.其中,网络分析法以现实路网为基础,并对道路进行阻力设置,以此模拟真实的公园绿地可达范围[12],其实质是以时间或距离等为成本进行分析,因而未能将居民实际需求纳入考虑范畴.两步移动搜索法(Two-step floating catchment area method,2SFCA)可较为充分地考虑公园绿地供给以及人口需求[13],此前常用于衡量就医空间等公共设施的可达性.国外方面,2SFCA 最早是由Radke等提出,由Luo 等进一步改进并命名为两步移动搜索法[14].之后Dai 采用改进的高斯两步移动搜索法对亚特兰大市的绿地进行可达性评估[15].国内方面,程岩等最早将2SFCA 应用于南京市郊区公园绿地可达性评估[16].此后,关于2SFCA 的应用研究不断发展,但截至目前,2SFCA 在城市公园绿地的应用较少.且多数相关文献的研究尺度多聚焦于街道、小区或者采取格网化的方式[17-19],上述尺度或方式在一定程度上影响可达性结果的准确性.2SFCA 所生成的空间作用域呈现标准圆形,而在实际情况中居民出行范围受路网等各类因素的影响,即搜索半径的不固定性.与此同时,2SFCA 的原式与引入衰减函数(高斯衰减函数)后的实际变化亦未被阐明.
采用网络分析法与高斯型2SFCA 量化梅州市中心城区公园绿地可达性.在研究过程中,将尺幅缩小至居住单元(房屋建筑),同时采用网络分析法修正2SFCA 运算过程中过于规整的空间作用域,以此提高可达性结果精度,并分析2SFCA 原式与改进式(高斯型衰减函数)的变化特点,为梅州市中心城区公园绿地规划建设提供科学依据.
1 研究区域
梅州市位于广东省东北部,介于东经 115°18′至116°56′,北纬23°23′至24°56′之间,下辖2个市辖区、1 个县级市、5 个县.其中梅江河呈几字形穿过城区,受河流分隔影响研究区域内人口分布和路网格局的空间分异显著.本研究以梅州市中心城区为主要研究范围,包括三角镇、城北镇、程江镇、扶大镇、金山街道、江南街道、西郊街道和新城办事处.按实际道路、河流等要素进行研究区域范围划分(图1),研究区域面积为81.92 km2,研究区内人口数量约为45.31 万人,公园绿地数量为15 个,公园绿地总面积为2.33 km2,占区域总面积的2.84%.
2 数据与方法
2.1 数据来源与处理
利用Bigemap 软件下载Google Earth 的2020 年梅州市高清卫星遥感影像数据(TIF)及梅州市街道(镇)级行政边界数据,根据研究需要解译遥感影像中的道路、公园绿地(最小面积为1 hm2)、公园绿地出入口、居住单元(居住房屋)等数据.采用公园绿地出入口作为实际到达公园绿地的标志,若公园绿地无特定出入口,则选择其拐角处或道路交叉口作为出入口.
依据上述数据分别建立梅州市中心城区的公园绿地数据库、道路数据库以及居住单元数据库.人口数据采用梅州市第六次人口普查资料,按照单个居住单元占总居住单元的面积比例求得各个居住单元的人口数据(表1).基于GIS 技术将获取的居住单元面数据以其质心为人口重心转换为居住点数据.并采用高清影像图比对、结合现场调研等方式修正数据(图1).
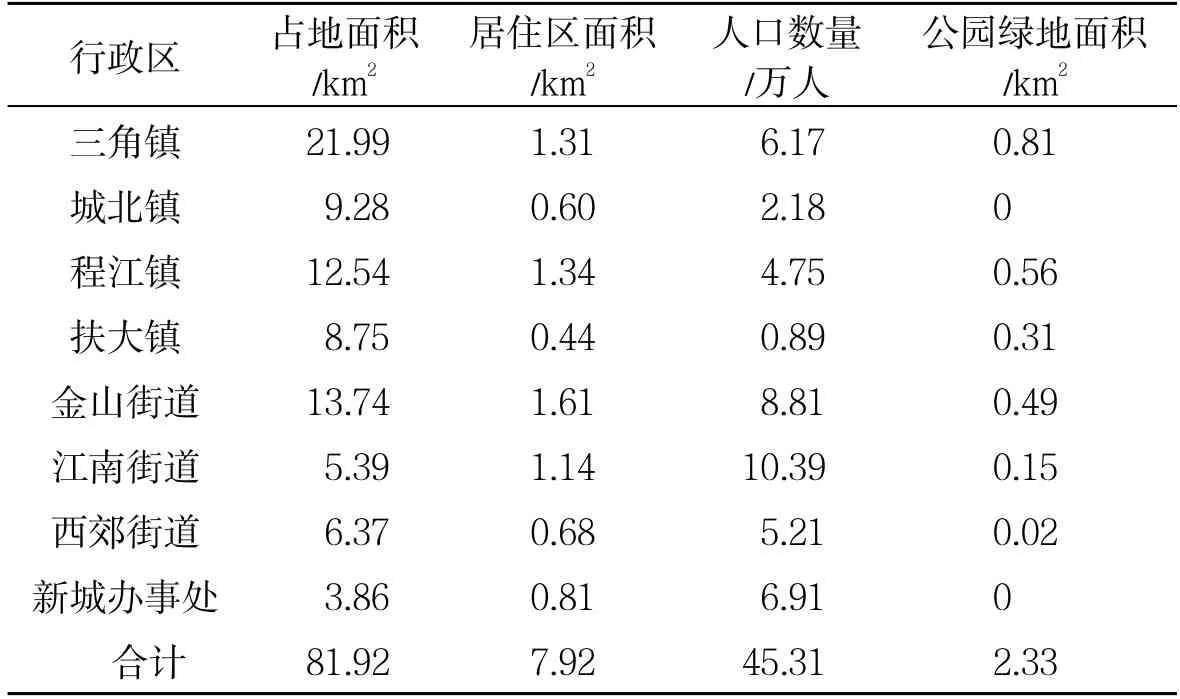
表1 行政区内面积、人口及公园绿地统计
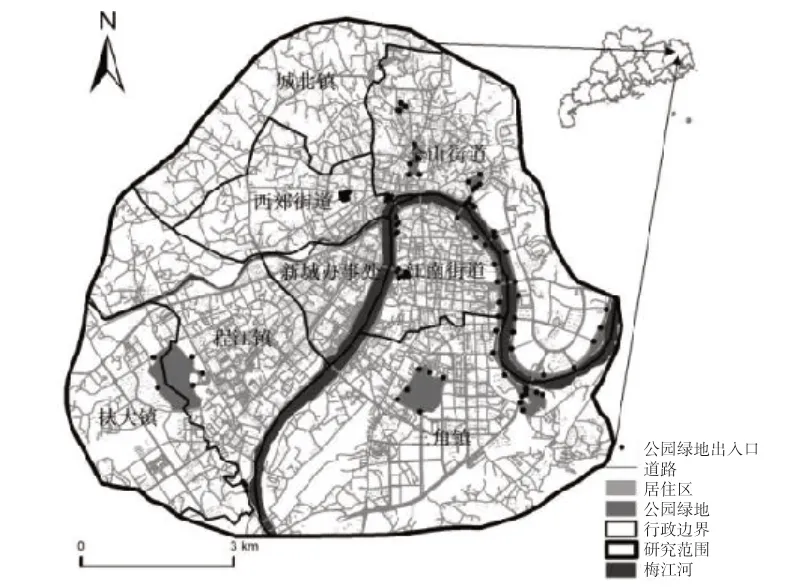
图1 道路、公园绿地、街道(镇)级行政边界
2.2 研究方法
(1)网络分析.网络分析(Network Analysis)是指对城市各类基础设施进行地理化和模型化的过程[9].网络中的中心、链、节点和阻力在本研究中分别以公园出入口、道路、道路交叉口以及通过某一条链耗费的费用及时间为代表.根据公园绿地的不同面积,进行服务半径的划定:≥3 000 m2的公园绿地,≥50 000 m2的公园绿地,≥100 000 m2的公园绿地,分别划定服务半径为500 m、1 000 m 以及2 000 m[20-22].并根据梅州市实际情况选择步行、骑行(摩托车)以及自驾(汽车)三种出行方式,基于道路宽度划分4 个等级并将其理论平均速度设定为实际速度.步行方式下设定步行速度1 m/s[9],骑行方式在1 到4 级道路上速度分别为60 km/h、40 km/h、30 km/h、20 km/h,自驾出行方式在 1 到4 级道路速度分别设定为70 km/h、50 km/h、35 km/h、25 km/h[23],上述出行方式的路口红绿灯等待时间均为设置为 30 s,选用上述数据及参数进行网络分析.采用可达面积比与可达人口比作为衡量网络分析可达性的指标,公式如 下[12]:式中,1为公园绿地的可达面积比,1为公园绿地面积,2为公园绿地可达范围(面积),2为公园绿地的可达人口比,1为公园绿地的服务人口数量,2为研究区总人口数量.
(2)高斯型2SFCA.2SFCA 可以较为全面地考虑公园绿地的供给以及人口需求,衡量居民可达公园绿地难易程度.由于2SFCA 在搜索半径内可达性相同,与需求点离供给点越近可达性越高的实际情况不符,相关文献引入距离衰减函数进行扩展.为探究引入高斯距离衰减函数后与原式的可达性计算结果之间的差异性,分别采用这两种公式进行可达性计算.以下公式为高斯型2SFCA,剔除高斯型距离衰减函数即为原式,公式如下[17]:
式中,为供需比; 为公园绿地j 在其空间作用域( ≤ )内居住单元的人口数量;是从居住单元k中心到公园绿地j 出入口的空间距离;为公园绿地设定的空间距离;为公园绿地面积;G( ,)是高斯型距离衰减函数;
3 结果与分析
3.1 基于网络分析法的公园绿地可达性
本研究选择从公园绿地服务范围(极限服务距离)和居民不同出行方式(时间)两种不同视角进行网络分析可达性度量.梅州市中心城区由于梅江河影响,其路网结构呈现团块状,致使网络分析结果展现出明显块状结构与平滑边缘.
由图2 可知,公园绿地可达范围基本分布在东部、东北部和西南部,位于研究区北部、西偏北和南偏西等地的城北镇、西郊街道、新城办事处、扶大镇南部、三角镇南部、程江镇东部及北部、金山街道北部未被公园绿地服务范围覆盖.由表2 可知,可达面积比合计为43.27%、可达人口比55.61%.不同出行方式会影响结果,下文将进一步研究在日常出行(步行)以及假期出行(骑行与自驾)的可达性.
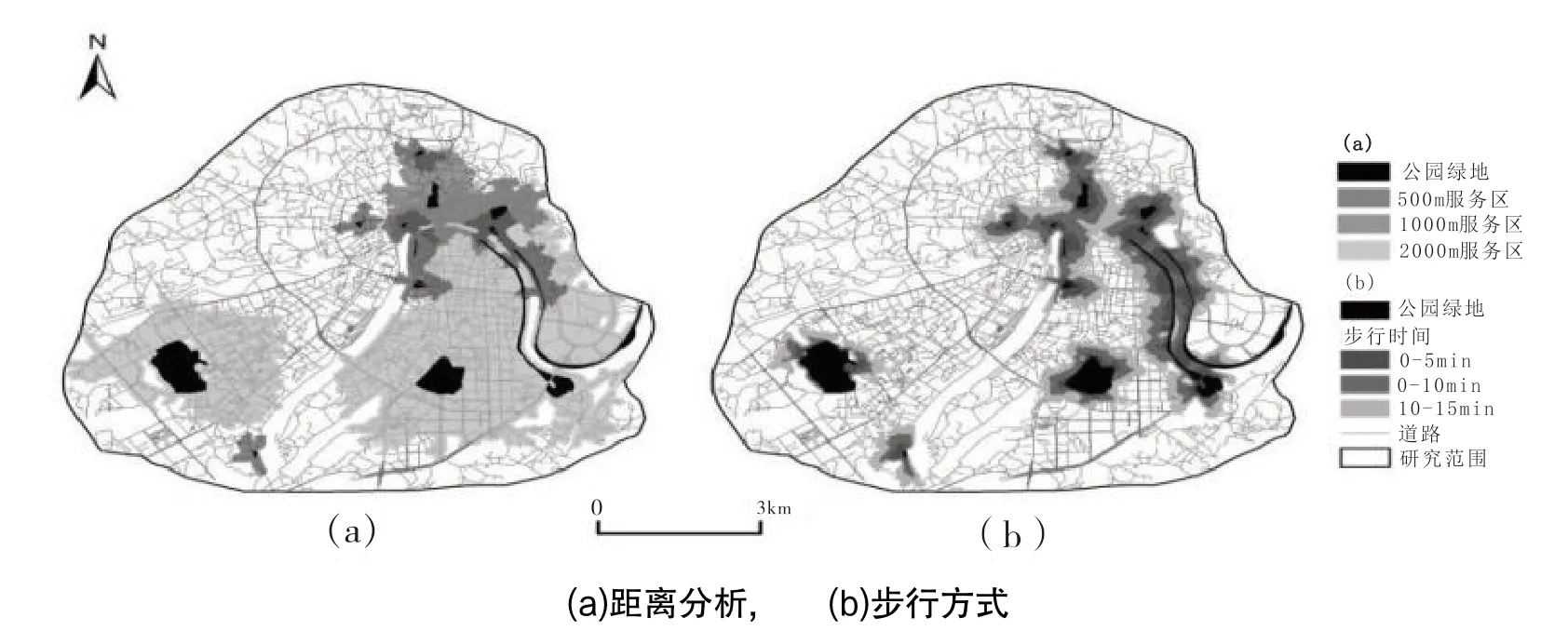
图2 城市公园绿地网络分析

表2 网络分析法可达性分析(公园绿地可达范围与步行方式)
步行为居民日常休闲生活中最主要的出行方式.确定0~5 min、5~10 min、10~15 min 三个时段的公园绿地服务范围(图3).在0~5 min、5~10 min、10~15 min 时段内,可达面积比依次为4.51%、7.04%、20.73%,可达人口比依次为4.38%、11.20%、15.22%(表3).由此可知,若采取步行出行方式,大部分地区的居民难以实现在较短时间内到达相应的公园绿地.
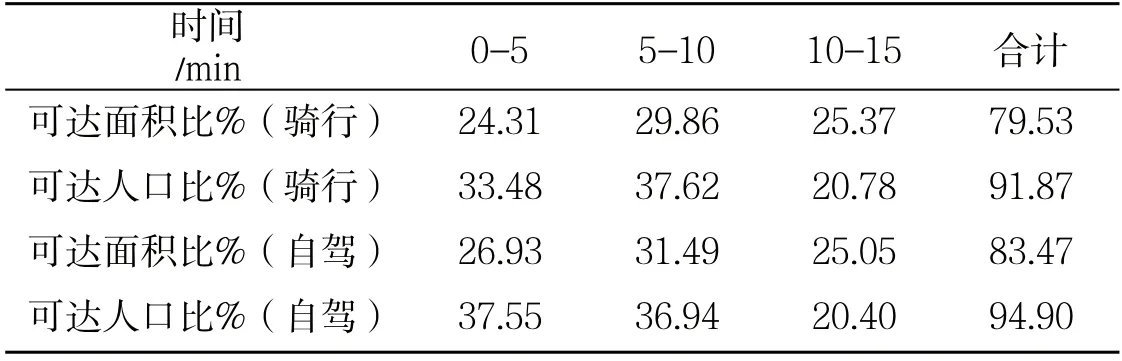
表3 网络分析法下城市公园绿地可达性(骑行与自驾方式)
由图3 可知,骑行与自驾方式下的公园绿地可达范围较接近,在三个时间段内的分布情况也较相似.经统计,在骑行条件下,总可达面积比为79.53%,总可达人口比为91.87%.私家车出行方式下,可达面积比为83.47%,可达人口比为94.90%(表4).与步行方式相比公园绿地的可达范围极大的增加,除研究区域东北部及南部等地区外,基本已覆盖整个研究区域.综合考虑网络分析法得到可达性,可知研究区域西北部、北部、中部、南部等大面积区域可达性低.

表4 2SFCA 下城市公园绿地可达性

图3 城市公园绿地网络分析
3.2 基于高斯型2SFCA 的公园绿地可达性
由于目前城市人口密度逐渐增大以及人口数量空间分布不均,可能出现供不应求或供过于求的情况.本研究采用高斯型2SFCA,进一步分析梅州市中心城区公园绿地与人口需求分布的空间耦合度.同时,为探究原式与引入高斯距离衰减函数后的可达性结果,以及考虑不同公园绿地的面积大小带来的吸引力差异,采用图2 的网络分析结果进行空间作用域修正,并分别进行原式与改进型的2SFCA 的计算[24-25].并利用克里金(Kriging)空间插值对居住单元 (18 100 个)可达性进行插值计算 .参照梅州市城市总体规划(2015-2030)中的人均公园绿地20 m2/人等指标作为克里金(Kriging)插值中断值的划定依据,结果如图4.
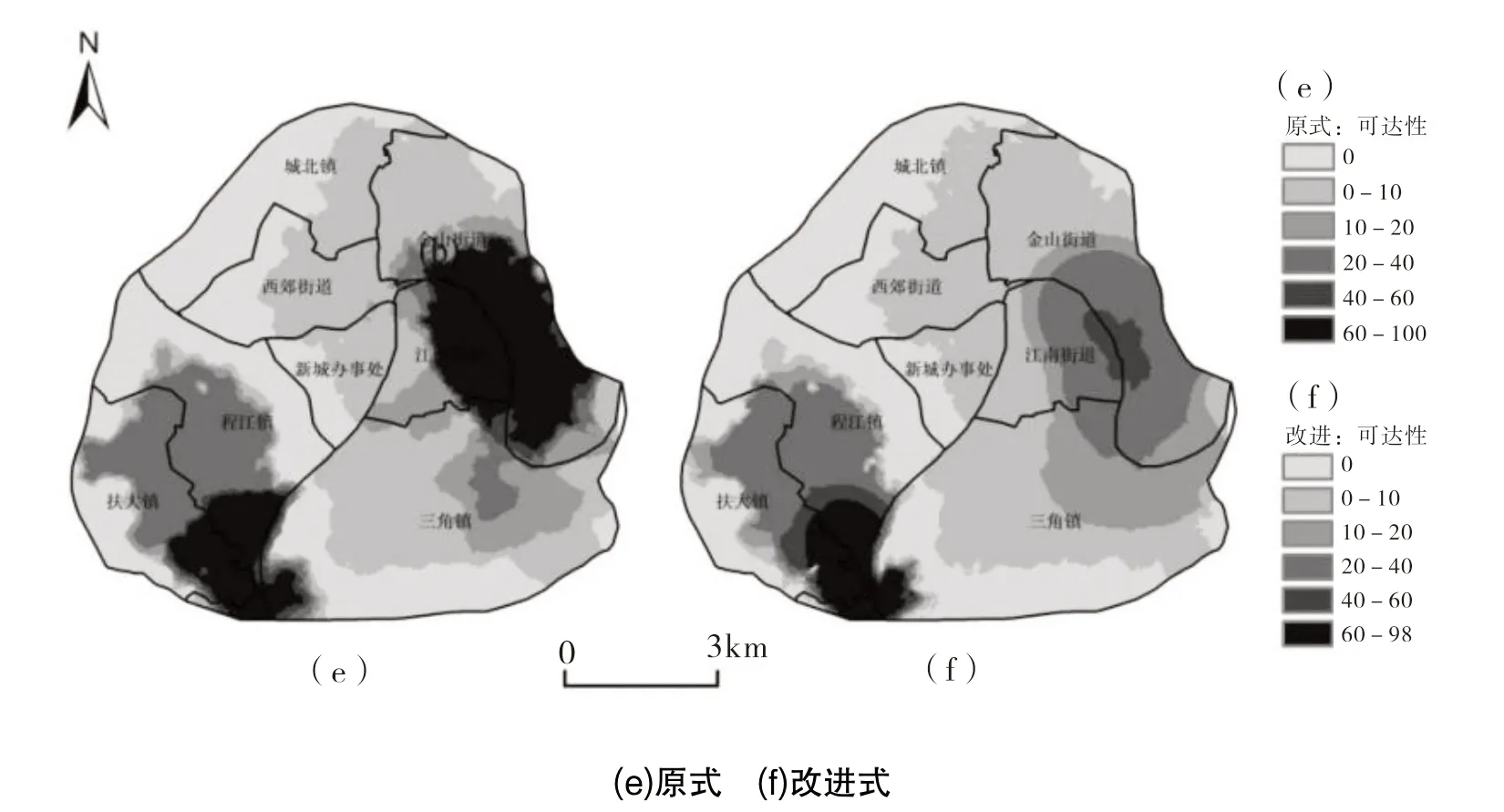
图4 2SFCA 公园绿地可达性分析
基于网络分析法修正后的2SFCA 可达性结果边缘呈现锯齿状,与居民实际出行范围更加契合,获得较为符合现实情况的可达性结果.对比图4 中原式与改进型的2SFCA 两种可达性结果,采用改进后方法计算的可达性结果比原式整体降低,但可达性总体分布基本一致,其空间差异主要在东北部与西南部的极值区域.研究区域东部及西南部地区,可达性较高,值在10 以上.城北镇西部、西郊街道西部、新城办事处西南部、程江镇北部及东北部、三角镇南部以及扶大镇西南部可达性为0,主要原因是这些区域未建设相应的公园绿地.可达性在0~10 之间的区域基本未建设公园绿地或人口需求大、供给不足,导致可达性降低.由表4 可知,原式较与改进式的可达性平均值大,但其相对数值大小较为一致.由于高斯型距离衰减函数的引入以及空间插值方法的选用,致使改进式可达性最小值出现负值,而在现实情况中未建设公园绿地情况的下应无可达性,故在实际应用中应进行相应处理.综合上述2SFCA 研究分析,研究区域内公园绿地供给与需求匹配情况较差,大多数地区可达性低.
4 结论与讨论
4.1 结论
基于2020 年梅州市高清影像数据,采用网络分析法进行公园绿地可达性计算.将研究尺度缩至居住单元,结合2SFCA 的原式及高斯型改进式,探讨梅州市中心城区公园绿地及人口分布的空间耦合度.
主要研究结论如下:
(1)依据网络分析结果,研究范围内西部、西北部以及南部边缘地带公园绿地不足.在步行方式下,大部分居民难以享受到公园绿地提供的休闲游憩服务,在骑行、驾车等方式下,其服务范围基本覆盖研究区域,但在研究区域西北部依旧未被覆盖;
(2)从供需的角度评价公园绿地与人口耦合情况,采用2SFCA 进行分析,研究区域整体可达性较低,可达性高值区仅位于东部及西南区.研究区域内公园绿地供给与需求匹配情况较差,难以满足城市居民对绿色空间的需求;
(3)本研究将2SFCA 中的研究尺度缩小至居住单元,在一定程度上提高了插值运算的准确性.并在计算过程中采用网络分析结果,避免了2SFCA 中空间作用域过于规整使得计算造成的误差.此外,对比分析了2SFCA 的原式及改进式,二者总体分布相差较小,但在极值区域展现出较大差异.总体而言,梅州市中心城区公园绿地与人口的耦合度低,应亟需对缺乏或供需不匹配的区域进行合理的公园绿地布局,满足居民日常游憩活动的需求.
4.2 讨论
本研究在对2SFCA 及其改进式的研究中发现,其以点状要素为中心,形成规整的空间作用域,与实际居民出行实际可达范围不相符[16].同时大多研究以街道等为研究尺度,易使插值结果偏离实际居住中心会造成较大误差[18].因此为提高2SFCA 的可达性计算的准确性,以居住房屋为基本单元(18100 个),以其质心为人口中心,减少基本单位面积过大带来的距离误差,并以网络分析结果为基础,剔除不在其可达范围内的居住单元,减小进行空间插值时的误差积累.采用网络分析结果中的实际居民出行范围对2SFCA 空间作用域进行修正这一方式具有普适性,也具有较强的可操作性,可应用于就医、养老等其他公共基础设施的2SFCA 的可达性计算中.
同时本文也存在诸多需改进的地方,第一,在应用网络分析时,对于公园绿地极限服务半径的确定仍需继续探讨[20],其易受到各类因素的影响,例如配套设施是否完善、景观吸引力是否足够等.第二,应用2SFCA 时,距离衰减函数的选择以及选取何种网络分析结果进行修正亦需进行讨论[14].第三,人口数据是由居住单元面积比例求得的,其推广性也需进一步研究[19],同时也并未考虑公园绿地受众群体的差异性.
梅州市中心城区形成了多个沿河分布的公园绿地,并呈现条带状,与传统的圆形或方形公园绿地有较大差异,如芹洋湿地公园、归读公园以及亲水公园等.就吸引力而言,此类公园绿地与传统的公园绿地之间的差异目前暂不明晰.因此对于因自然因素如河流、地形等所形成的公园绿地,其服务范围无法类似于平原型城市内部的公园绿地向四周提供服务,而呈现为单一方向的.在此后研究中应对考虑河谷型城市公园绿地的独特价值进而实现合理布局.

