复合式连拱隧道曲中墙施工力学行为时空演化规律

徐 晴， 张素磊, ， *， 刘 昌， 张国栋， 陈德刚

(1. 青岛理工大学土木工程学院， 山东 青岛 266033； 2. 青建集团股份公司， 山东 青岛 266071；3. 北京交通大学 城市与地下工程教育部重点实验室， 北京 100044)

0 引言

我国早期修建的连拱隧道主要为整体式直中墙形式，由于复合式中墙连拱隧道具有相对完善的防排水系统，已逐步应用于隧道工程。由于隧道施工过程中力学演化规律复杂[1-4]，中隔墙作为连拱隧道主要承载结构，其力学特性决定了隧道结构的稳定性，因此近年来中隔墙一直是研究的重点和热点。

国内外学者主要采用现场监测、数值分析及模型试验等方法对中隔墙力学特性展开研究。例如： 邱军领等[5]基于现场试验对黄土地区某整体式连拱隧道中隔墙内力进行了系统测试，其研究成果对黄土地区连拱隧道设计、施工具有重要参考价值； 丁智等[6]通过现场监测获取了施工各阶段中隔墙不同部位应力分布特征，指出中隔墙中部为受力薄弱位置； 杨果林等[7]依托某公路双连拱隧道对中隔墙主筋轴力及基底压力进行了监测，提出隧道主洞上台阶开挖引起的围岩卸载是造成中隔墙内力增大的主要因素； 周丁恒等[8]针对浅埋大断面连拱隧道探讨了不同施工阶段直中墙轴力变化规律，研究表明连拱隧道繁琐的施工工序是造成中墙内力变化的重要原因； 邱长林等[9]基于室内模型试验，对施工阶段连拱隧道直中墙应力分布规律进行了分析； 瞿永等[10]介绍了一种中隔墙主应变监测新方法，发现中隔墙应力主要为围岩荷载引起的竖向应力； 胡长明等[11]通过数值分析，从力学机理层面分析了掌子面纵向间距及仰拱开挖长度等施工参数对中隔墙稳定性的影响机制； Yang等[12]基于室内试验模拟，指出连拱隧道中隔墙顶部是保证结构稳定性的重点关注部位； Lai等[13]建立地震反应模型，分析了中隔墙的抗震特性； Yan等[14]通过现场监测结果发现靠近中隔墙一侧初期支护与围岩之间的接触压力小于其他部位； Zhang等[15]分析了中隔墙背后空洞条件下连拱隧道结构力学特性，结果表明中隔墙底部为结构最薄弱部位。综上，关于施工阶段中隔墙内力的研究已取得较丰硕的成果，对于指导连拱隧道的施工具有重要意义。

连拱隧道非对称施工会导致中隔墙承受显著的偏压，例如： 曾宪营等[16]对施工阶段连拱隧道中隔墙顶部压力进行了监测，分析后发现中隔墙始终存在向先行洞一侧的弯矩； 李建宇等[17]通过现场监测发现连拱隧道非对称施工导致钢筋轴力呈非对称分布； Huang等[18]通过对非对称地层连拱隧道现场监测，发现中隔墙承受小偏压荷载一侧裂缝扩展更为严重； Wang等[19]结合现场监测结果发现，中隔墙应力经多次施工转换后具明显偏压特征； 杨果林等[20]指出施工期间中隔墙偏转降低了隧道稳定性； 夏永旭等[21]采用线弹性应变计算模型，分析了中隔墙在隧道开挖过程中的偏转变形效应； 邱明明等[22]发现隧道先开挖一侧更易引起曲中墙结构破坏； 王胜辉等[23]研究发现连拱隧道非对称开挖使得直中墙承受较大的偏心荷载； Li等[24]分析得出中隔墙部位应力分布具有复杂性及非对称性的特点。

综上可见，连拱隧道非对称施工会造成中隔墙承受显著偏压现象，恶化了隧道结构力学特性。然而，目前关于连拱隧道的研究主要集中在中隔墙应力分布规律及变形特征方面，而曲中墙施工阶段的力学状态决定着连拱隧道的施工安全性，却未见关于隧道开挖时空效应及中隔墙自身构造对曲中墙应力分布及偏压效应影响的研究。为弥补既有研究不足，依托在建复合式曲中墙连拱隧道，采用数值分析及现场监测等方法对施工阶段曲中墙应力演化规律及偏压效应进行系统分析； 在此基础上，分别就连拱隧道主洞开挖步距及中隔墙自身厚度对曲中墙偏压效应影响机制进行剖析，以期为复合式曲中墙连拱隧道的设计及施工提供参考。

1 工程概况

本文所依托的隧道工程位于浙江省杭州市淳安县，隧道为双向4车道，起讫里程为K38+613～+994，全长381 m，最大埋深60 m，设计时速80 km，隧道净高10.35 m，总跨度24.56 m。隧道位于低山丘陵带，洞身穿越中风化粉砂岩、局部夹砂砾岩，围岩结构呈碎裂状，开挖过程中存在渗水、滴水等现象。隧道支护结构为复合式衬砌，初期支护由喷射混凝土、钢拱架、钢筋网及锚杆组成，二次衬砌及中隔墙为C30模筑混凝土。隧道支护参数见表1，隧道洞口照片见图1。

表1 隧道支护参数

连拱隧道先开挖中导洞，然后浇筑中隔墙，主洞采取上、下台阶法交替施工，具体施工步骤如下： 1)开挖中导洞、施作临时支护； 2)中导洞开挖结束后施作中隔墙； 3)开挖左上台阶； 4)施作左洞拱部初期支护； 5)开挖左下台阶； 6)施作边墙初期支护； 7)施作左洞仰拱； 8)施作二次衬砌。上述2)—6)步骤施工完成后，进行右洞施工，具体施工步骤根据现场情况进行调整。施工工序见图2。

(a) (b)

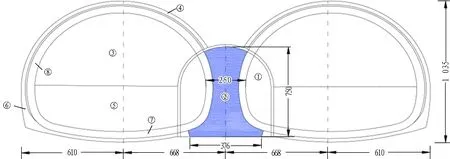
图2 施工工序图(单位： cm)

2 计算模型建立

基于有限元软件ABAQUS对复合式连拱隧道施工阶段曲中墙力学特性及偏压效应进行分析。选取隧道K38+690～+750段建模计算，围岩采用摩尔-库仑本构模型，围岩级别为Ⅳ级，中隔墙、初期支护均假设为均匀线弹性材料，中隔墙及支护结构均采用C3D8R实体单元模拟，其中，钢拱架采用等效刚度折算到初期支护及中隔墙的弹性模量中[25]。计算模型中材料力学参数来源于现场钻探资料，见表2。

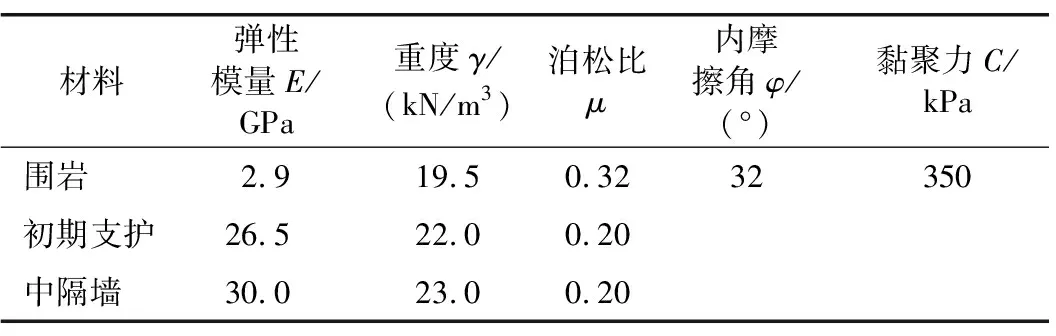
表2 材料力学参数

为减小边界效应对隧道开挖的影响，计算模型在隧道两侧取约4倍洞径，计算模型中隧道埋深与现场监测断面埋深一致，按照30 m考虑，模型尺寸为110 m×80 m×60 m。计算过程中分别限制模型底部、两侧、前后边界面的法向位移。数值计算网格模型如图3所示。

图3 数值计算网格模型

建模分析时，中隔墙在中导洞开挖后施作。隧道左线为先行洞，右线为后行洞，2个主洞之间的开挖步距为30 m，采用上下台阶法进行开挖。上、下台阶开挖间距为15 m，每个开挖步3 m。在施工步1—20时仅左洞开挖，在施工步21时右洞开挖，左、右线之间保持20个施工步距。计算过程中的施工工序见图4。考虑到围岩的应力释放过程，初期支护延后1个施工步施作。本文重点分析隧道施工阶段中隔墙的力学演化规律，计算过程不考虑二次衬砌。

图4 计算工序示意图

3 施工阶段曲中墙力学特性

3.1 曲中墙应力分布特征

图5示出了左洞上台阶开挖至Z=30 m时(Z为纵向开挖深度)曲中墙水平和竖向应力分布。由图5可见，先行洞(左洞)开挖后，因左侧隧道围岩应力释放导致曲中墙已开挖段承受非对称荷载，具体表现为： 1)后行洞一侧中隔墙顶部水平应力大于先行洞一侧，而先行洞一侧中隔墙底部水平应力明显大于后行洞一侧，其中最大水平应力为3.50 MPa，位于后行洞一侧曲中墙顶部； 2)曲中墙靠近先行洞一侧竖向应力大于后行洞一侧，且曲中墙竖向应力远大于水平应力。

(a) 水平应力

(b) 竖向应力

选取隧道开挖方向Z=30 m处曲中墙横断面应力分布情况进行重点分析，如图6所示。由图6(a)可见，水平应力在曲中墙顶部两侧集中，中部应力水平较低，水平应力沿曲中墙中轴线呈近似对称分布；由图6(b)可见，先行洞开挖导致曲中墙左侧中部竖向应力明显高于右侧，且在曲中墙高度方向上呈“中部大、两端小”的分布特征。综上可知，施工阶段曲中墙主要承受竖向应力，与文献[9]结论一致，而连拱隧道非对称开挖显著改变了曲中墙竖向应力分布规律，导致曲中墙承受偏压荷载。

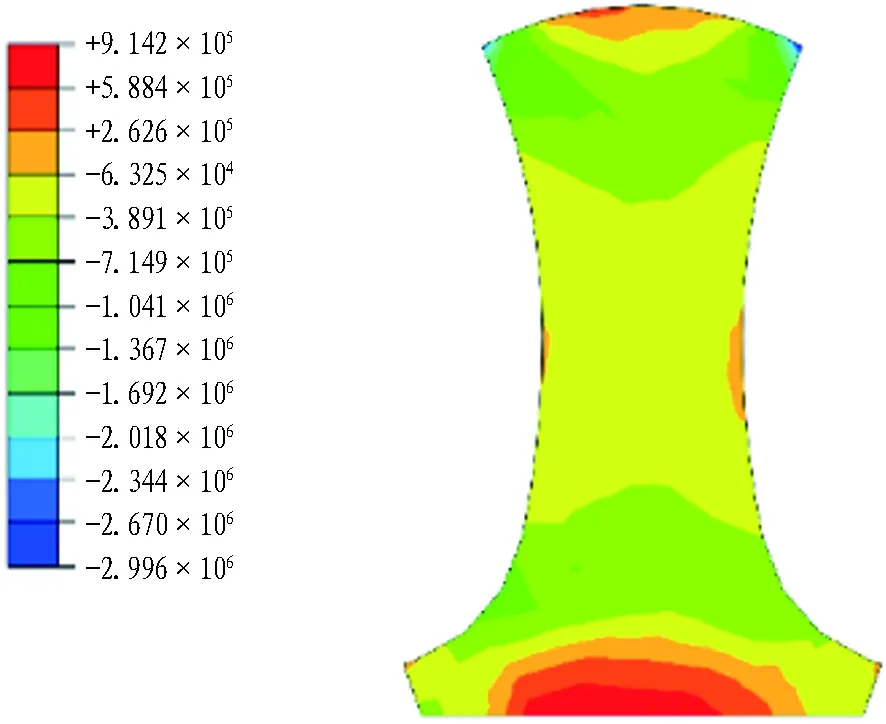
(a) 水平应力

(b) 竖向应力

3.2 曲中墙竖向应力演化规律

选取Z=30 m处曲中墙横断面左、右两侧的上、中、下共6个特征点竖向应力进行分析，如图7所示。图中1#、2#为上部特征点，3#、4#为中部特征点，5#、6#为下部特征点。由图可见，整个施工阶段曲中墙竖向应力经历了“缓慢增长阶段”、“快速增长阶段”及“减速稳定阶段”，其中“快速增长阶段”为主要应力增长阶段，在距掌子面-1D～1D(D为洞径)处。左上台阶开挖后，左洞围岩应力释放，中隔墙左侧应力急剧增大，此阶段中隔墙右侧应力呈微弱增大趋势， 曲中墙中部竖向应力明显大于顶部和底部，导致曲中墙中部承受明显的偏压荷载；左下台阶开挖后，围岩逐渐由“二次应力状态”过渡到“三次应力状态”，此时中隔墙左侧应力增大速率逐渐减缓；右上台阶开挖后，中隔墙右侧应力迅速增大，直到右下台阶开挖后右侧应力趋于平缓，右侧隧道开挖对中隔墙左侧应力分布影响较小。开挖结束后，曲中墙两侧同一截面处应力终值相差不大，说明施工开挖顺序对最终应力影响不大。

图7 曲中墙竖向应力变化曲线图

图8示出曲中墙在A-A截面上的竖向应力分布曲线。由图可见，中隔墙竖向应力在A-A截面呈“端部小、中部大”的分布特征，曲中墙竖向应力稳定后最大值位于中隔墙中部，达到5.24 MPa。从施工过程来看，当开挖面距监测断面-1D～1D时应力曲线变化幅度明显增大，而当开挖断面超过监测断面1D后应力变化率逐渐减小，最终应力值趋于稳定。分析可见，曲中墙上下两侧应力终值相差不大，而竖向应力最大值位于曲中墙横断面上最小截面位置(B-B截面)，应是施工过程中重点关注部位。

图8 曲中墙竖向轴线上竖向应力分布(单位： MPa)

3.3 中隔墙偏压效应分析

曲中墙中部为竖向应力集中区域，这里选取曲中墙横断面最小截面(图8中B-B截面)进行偏压效应分析。在此之前对B-B截面竖向应力分布规律进行分析，由3.2节中已知应力“快速增长阶段”为应力主要增长阶段，因此，重点对本阶段应力进行分析。图9示出B-B截面在“快速增长阶段”竖向应力分布曲线。拟合曲线斜率为0.117—2.001—0.245，说明应力偏压现象在施工过程中呈先增大后减小现象。

图9 曲中墙B-B截面竖向应力分布曲线

曲中墙偏压效应如图10所示，这里引入截面弯矩M来描述曲中墙的偏压效应。σ左、σ中、σ右分别为中隔墙左侧、中部及右侧应力值，H为中隔墙厚度。B-B横截面在单位纵向长度上的弯矩

M=M左-M右。

(1)

式中：M以逆时针方向为正；M左、M右分别为左、右侧应力对轴线求弯矩，Mi(i=左，右)可按式(2)求解：

(2)

图10 曲中墙偏压效应示意图

图11示出施工阶段曲中墙偏压弯矩分布曲线。由图可见，连拱隧道先行洞开挖后，中隔墙在逆时针偏压弯矩作用下向先行洞一侧偏转，先行洞下台阶开挖后中隔墙偏压弯矩达到峰值780 kN·m；后行洞的开挖使得中隔墙靠近后行洞一侧应力迅速增大，中隔墙两侧应力差缩小，此阶段偏压效应逐渐削弱。施工完成后中隔墙始终存在着向先行洞一侧的弯矩，偏压效应并未完全消除，表明先行洞施工对中隔墙受力性能的影响大于后行洞。

图11 曲中墙偏压弯矩分布曲线

3.4 曲中墙内力现场监测分析

3.4.1 监测项目与测点布置

对复合式连拱隧道曲中墙压力及钢筋轴力进行现场监测，主筋轴力测试采用JTM-V1000H系列振弦式钢筋计，曲中墙压力测试采用型号为JTM-V2000D振弦式土压力计。在曲中墙K38+723断面两侧主筋上各布设3个钢筋计，在顶部及底部各布置3个压力盒，传感器布置见图12。

(a) 现场布置情况 (b) 布置示意图

3.4.2 中隔墙压力分析

图13示出曲中墙顶部及底部压力监测时程曲线。曲中墙施作后，围岩荷载由临时支护逐渐传递到曲中墙，受隧道左、右线开挖多次扰动，压力时程曲线波动幅度较大。从压力曲线整体变化趋势来看，上台阶开挖后应力迅速增大，且曲中墙上部受开挖影响大，因此，重点选取顶部压力盒M1—M3的压力变化过程进行分析。左洞上台阶开挖后，M1、M2、M3的压力值分别为-0.72、-0.64、-0.43 MPa； 随着围岩荷载增大，围岩压力由曲中墙左侧转移至中部及右侧，当开挖至左洞下台阶时，M2、M3的压力值达到-1.03、-0.82 MPa；随着右洞上台阶开挖，右侧M3的压力值增长至1.25 MPa，此阶段M3增幅达52%，同时M1、M2压力值缓慢增大； 监测到第95 d时，右侧下台阶开挖后曲中墙压力逐渐稳定。M1、M2、M3压力盒最终压力值分别为-1.55、-1.29、-1.47 MPa，M4、M5、M6最终压力值分别为-1.20、-1.04、-1.22 MPa，说明曲中墙顶部受围岩荷载的影响程度要大于底部区域。

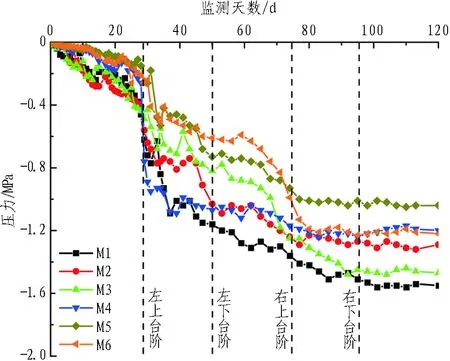
图13 曲中墙压力实测曲线图

将数值计算及现场监测曲中墙左上、左下、右上、右下台阶分别开挖至监测断面-1D～1D应力增量的比例进行了统计，如图14所示。主洞上台阶开挖对同侧曲中墙应力影响显著，本阶段应力增量约占整个施工阶段的50%，并且先行洞上台阶开挖对中隔墙应力分布的影响大于后行洞上台阶开挖。数值计算和现场监测分析所得的各阶段应力占比基本接近，验证了数值计算结果的可靠性。

3.4.3 曲中墙主筋轴力及偏压效应分析

图15示出曲中墙主筋轴力实测曲线，负值表示结构承受压力。由图可见，0—20 d曲中墙开始承载，钢筋轴力逐渐增大，到20 d后导洞位置处围岩应力释放基本完成，钢筋轴力暂时稳定。在25—40 d，隧道左洞上台阶开挖，当左洞上台阶开挖至监测断面时，同侧曲中墙内力急剧增大，曲中墙在非对称荷载作用下出现向先行洞一侧的偏转现象。当后行洞上台阶开挖至监测断面时(60—80 d)，右侧R1—R3轴力迅速增大，此阶段L1—L3轴力呈缓慢增大趋势，后行洞下台阶开挖后(100 d之后)钢筋轴力趋于稳定，施工结束后曲中墙两侧钢筋轴力值接近。从曲中墙主筋轴力变化过程来看，主洞上台阶开挖是轴力增大的主要原因，且上台阶开挖对同侧曲中墙钢筋轴力影响显著，这与第3.2节中数值计算获取的曲中墙应力演化规律相同，进一步验证了数值分析的可靠性。

(a) M1

(b) M3

中隔墙横截面上分布不均的竖向应力导致其承受偏压荷载，进一步对曲中墙偏压现象进行分析。为简化分析假设中隔墙处于单向偏压状态[26]，由材料力学组合变形计算公式可得结构应力

(3)

式中：N为结构轴力；A为截面面积；Mz为中隔墙弯矩；Iz为中隔墙惯性矩；y为作用点到中心点的距离。

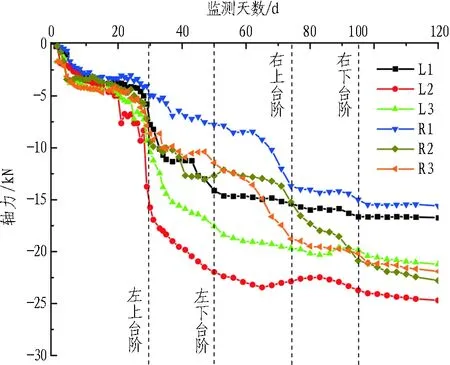
图15 曲中墙主筋轴力实测曲线图

根据共同变形理论，假设中隔墙钢筋与混凝土共同变形，结合胡克定律，可由式(4)计算中隔墙弯矩：

(4)

式中：NL、NR为左、右钢筋计轴力；E为混凝土弹性模量；ES为钢筋计弹性模量；AS为钢筋计截面积；Iz为中隔墙惯性矩，Iz=bh3/12，h为中隔墙宽度，b为轴向单位长度。

曲中墙弯矩时态曲线如图16所示。由图可见，连拱隧道先行洞开挖后，中隔墙在非对称竖向应力作用下出现偏压效应，中隔墙弯矩在隧道一侧施工转到双侧施工过程中变化幅度较大；后行洞开挖后，右侧围岩应力释放中和了中隔墙偏转效应，弯矩值逐渐减小，其中，曲中墙中部L2-R2截面弯矩最大值为1 170 kN·m，大于L1-R1截面及L3-R3截面弯矩最大值(见图12(b))。由于施工现场爆破扰动及支护不及时等因素，现场监测得到的中隔墙L2-R2截面弯矩值1 170 kN·m大于数值计算的780 kN·m，但两者的变化规律基本一致。

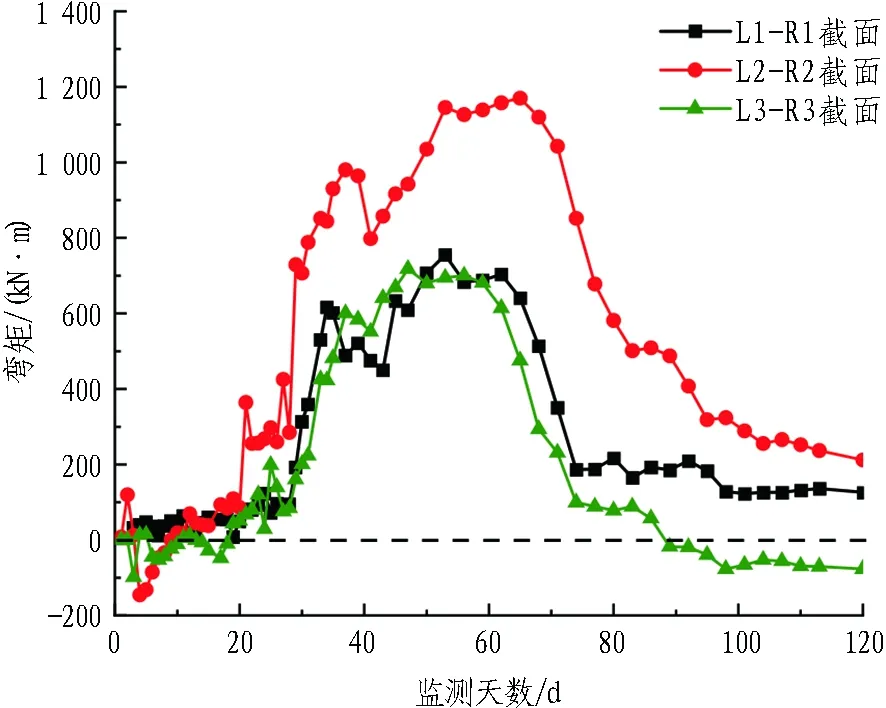
图16 曲中墙弯矩时态曲线

4 曲中墙应力及偏压影响因素分析

中隔墙设计是连拱隧道的关键环节，《公路隧道设计规范》提出了连拱隧道中隔墙最小厚度的概念，规定复合式连拱隧道中隔墙厚度不宜小于2 m(包括二次衬砌厚度)。但是，已有的关于中隔墙厚度设计值均是基于已有工程经验而来，对于保持稳定不开裂的中隔墙厚度并不明确，不同厚度的中隔墙在非对称施工荷载下的力学特性及偏压效应有待探究；并且，已有大量研究表明连拱隧道开挖间距对中隔墙稳定性影响较大。基于此，本节从设计、施工层面就中隔墙厚度及主洞施工步距对曲中墙应力及偏压影响进行分析。

4.1 曲中墙厚度对其应力及偏压影响

本文所依托的连拱隧道曲中墙厚度H=1.7 m(不包括二次衬砌厚度)，这里分别对H为1.3、1.5、1.9、2.1 m情况下曲中墙力学特性及偏压效应进行分析，如图17所示。需要说明的是，各工况下隧道尺寸相同，且模型尺寸及参数等与第2节所述计算模型一致。根据3.2节分析可知，主洞上台阶开挖对曲中墙应力分布的影响显著大于下台阶开挖。为提高计算效率，研究曲中墙厚度对其应力及偏压效应的影响时，采用全断面施工方法，主洞施工步距为30 m。

图17 不同厚度曲中墙(单位： m)

选取曲中墙横断面上最小截面进行分析，曲中墙左侧不同厚度下竖向应力变化曲线见图18。由图可见，随着曲中隔墙厚度H的增大，中隔墙承载能力提高，隧道施工阶段曲中墙应力整体呈减小现象，在图中表现为应力分布曲线整体上移。当曲中墙厚度减小至1.3 m时，中隔墙承载能力大幅下降，隧道开挖引起的曲中墙竖向应力显著增大，且当后行洞施工后应力仍然增大，表明中隔墙已有失稳趋势。从曲中墙应力演化过程来看，当H≥1.5 m时，中隔墙承载能力提高显著，主洞开挖仅引起同侧曲中墙应力急剧增大，曲中墙另一侧应力呈微弱减小现象；当曲中墙厚度减小至1.3 m后，曲中墙承载面积减小，此时，在隧道施工阶段曲中墙全截面承载，曲中墙整体应力受隧道开挖影响较大，且最终应力值较H≥1.5 m时有大幅提高。

图19示出曲中墙厚度不同时截面偏压弯矩分布曲线。由图可见，无论中隔墙厚度如何，非对称施工均会导致曲中墙发生偏转，曲中墙厚度不同时表现出不同的偏压效应。H=2.1 m及H=1.3 m时，曲中墙弯矩均有大幅度减小，但两者受力状态迥异，即H=2.1 m时，曲中墙承载能力提高，中墙应力减小使得偏压弯矩大幅减小；而H=1.3 m时，曲中墙承载面积减小，导致结构全截面承受较高应力，两侧应力值相差较小，因此结构偏压弯矩较小，此时中隔墙可能由于承载能力不足发生屈服失效。此外，台阶法施工时曲中墙最大弯矩值较全断面开挖时的最大值降低8%。因此，考虑到曲中墙的应力分布、偏压效应、稳定性及经济性等，建议单线2车道双连拱隧道曲中墙厚度设计值取1.5～1.9 m。

图18 曲中墙左侧竖向应力变化曲线

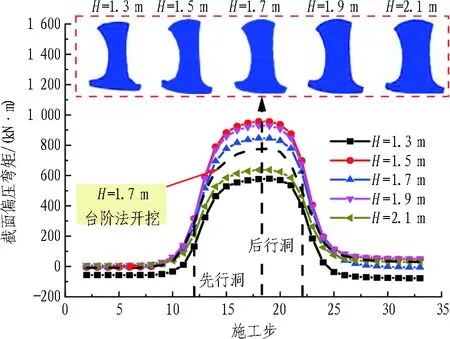
图19 不同厚度曲中墙偏压弯矩曲线

4.2 隧道主洞施工步距对曲中墙应力及偏压影响

取主洞施工步距l分别为0、6、12、18、24、30 m进行分析，如图20所示，模型尺寸及参数与第2节所述计算模型一致，同样采用全断面施工方法。

图20 主洞不同开挖步距(单位： m)

图21示出连拱隧道主洞不同施工步距l下曲中墙中部竖向应力曲线。

(a) 曲中墙左侧

(b) 曲中墙右侧

首先，对先行洞一侧曲中墙中部A点处的竖向应力进行分析，由于各工况下左洞开挖至监测断面的时间一样，在开挖至断面约1D范围内时应力开始增大，但各工况下应力变化规律基本相同。后行洞开挖至监测断面1D范围内时，应力增大速率逐渐减缓，直至开挖到监测断面后，应力开始减小，当掌子面距A点1D距离后，应力值达到稳定。图21(b)为曲中墙中部右侧应力变化曲线，可见，随着l的增大，B点应力曲线整体往右上方偏移，应力增大阶段“延迟”。当先行洞开挖至目标断面之前，各施工步B点应力变化规律一致；随着l的增大，非对称开挖造成曲中墙在偏压荷载作用下发生向先行洞一侧的偏转越显著，导致曲中墙右侧存在某种意义上的“拉作用”，因此，在后行洞距监测断面1D之前，B点应力呈减小现象，且l越大应力减小幅度越大；当后行洞开挖至监测断面1D范围之内，B点应力逐渐增大，应力增大速率在后行洞开挖至监测断面时达到峰值。

通过上述分析可得，l显著影响施工过程中曲中墙应力变化规律，但不改变应力终值，因此，施工过程中曲中墙工作性能评价尤为重要。图22示出不同施工步下曲中墙偏压弯矩曲线，可见，随着主洞施工步距l的增大，曲中墙偏压弯矩最大值越大，且曲中墙偏转效应持续时间越长。

图22 不同施工步距下曲中墙偏压弯矩曲线

图23示出不同l时曲中墙弯矩最大值分布曲线。横轴为主洞开挖步距l(已换算成洞径D的倍数)，对最大弯矩值与l的关系进行了拟合：

(5)

对拟合公式进行一次求导，得到弯矩拟合曲线梯度：

(6)

由图23可见，曲中墙截面最大弯矩值随开挖步距l增大而增大，但增大速率随l增大逐渐减小。根据《公路隧道设计规范》，连拱隧道施工时两主洞宜保持1～2倍洞径以上的距离，忽视了连拱隧道非对称开挖对曲中墙力学特性的影响。因此，结合本文研究结果，综合考虑曲中墙应力分布、偏压效应及主洞施工干扰等因素，建议连拱隧道主洞施工步距保持在1D～2D。

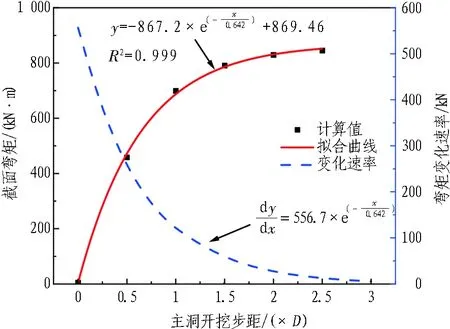
图23 不同施工步距下截面最大弯矩

5 结论与讨论

1)复合式连拱隧道施工过程中曲中墙竖向应力经历了“缓慢增长阶段”、“快速增长阶段”及“减速稳定阶段”；主洞上台阶开挖对中隔墙内力分布规律影响显著，曲中墙中部为受力最不利部位。

2)连拱隧道非对称开挖造成曲中墙承受偏压荷载，导致曲中墙发生向先行洞一侧偏转现象，偏转现象在先行洞上台阶开挖至后行洞上台阶之间最为显著，施工完成后中隔墙始终存在向先行洞一侧的偏压弯矩。

3)曲中墙厚度对施工阶段曲中墙应力分布、偏转效应影响显著，当曲中墙厚度为1.3 m时，中墙承载能力大幅下降，综合考虑到曲中墙稳定性及工程经济性，对于单线2车道双连拱隧道曲中墙厚度建议值为1.5～1.9 m(不包括二次衬砌厚度)。

4)主洞施工步距对曲中墙应力分布影响较大，但不改变曲中墙应力终值； 其次，曲中墙偏压弯矩随施工步距l增大而增大，且偏转效应持续时间越长，建议单线2车道双连拱隧道主洞施工步距保持在1D～2D。同时，选择合理施工方法及加强应力集中区域的配筋率也是避免曲中墙在不利偏压荷载作用下出现开裂、倾覆失稳等的重要措施。

本文主要采用数值计算及现场检测方法来对曲中墙连拱隧道力学演化机制及偏压效应进行研究，后续将开展室内模型试验，与其结果进行对比验证。