基于无监督学习的医学图像分割算法

何 斌,臧义华,梁 佳

(中国电子科技集团公司第十五研究所，北京 100083)

1 引言

脑是复杂的系统之一[1]，对脑的探索是人类生命本身和自然界现象的终极疆域，是挑战性很强的前沿研究之一。基于核磁共振图像分割技术，构建宏观“大脑地图集”，是研究大脑的结构和功能最直接、有效的方法，对于认识脑、保护脑、创造脑具有重要意义[2]。然而，由于大脑组织结构和功能复杂，不同个体之间差异较大；且磁共振成像过程中容易受到场偏移效应、组织运动等影响，物理噪声大，这些给医学图像分割算法带来较大的挑战。

1980年以来，聚类方法被应用到核磁共振图像的分割[3]，但由于算法本身的局限性，选择合适的聚类数一直是瓶颈问题。本文提出一种基于无监督学习的大脑核磁共振图像分割方法。首先，基于FSL 综合软件工具库对数据进行预处理，主要包括运动校正、失真校正、图像配准等[4-5]。然后利用纤维追踪技术求得感兴趣脑区到全脑体素点的连接矩阵，并基于最小二乘和非线性拟合算法构建主成分分析流程框架，确定聚类数目。最后以感兴趣脑区到全脑体素点的连接的特征矩阵作为输入，利用谱聚类算法实现大脑核磁共振图像分割。

2 基于连接的脑图像分割

弥散张量成像是一种较新的利用各向异性弥散来估计大脑组织结构的磁共振成像技术，由于安全无创性，被广泛的应用于人脑和非人灵长类动物的脑图像分割。其基本原理是根据大脑组织中水分子的弥散特性，通过施加梯度脉冲使磁场环境发生变化，进而影响质子产生共振，然后通过检测水分子的运动状况，对变化的信号进行测量估算，经过仪器处理输出不同组织的图像信息。

弥散张量模型通过D 来表征水分子在三维空间的弥散特性，由6 个变量组成的三维对称正定矩阵来描述，具体表示如下：

其中，Dij表示的是水分子在不同方向上的弥散属性，i，j[x，y，z]。基于上述6个扩散参量对应的特征是可以通过计算进一步度量多种水分子的扩散特性指标，比如各向异性FA和相对各向异性RA等，如下所示：

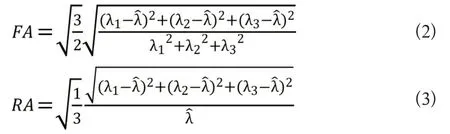
3 脑图像分割算法

3.1 数据预处理

3.1.1 图像校正

由于涡流畸变和组织运动，需要对图像产生的伪影进行校正。首先，基于磁共振图像提取出未施加扩散梯度脉冲的参考图像(b0 像)，然后以b0 像为标准，基于高斯过程(Gaussian Process，GP)对扩散信号建模，通过涡流校正(Eddy Current)对图像切片的扭曲和运动失真信号进行调整纠正，最后计算体素的扩散张量模型，得到不同方向上的特征值和每一个体素的张量估计和弥散属性分布。

3.1.2 图像配准

配准是图像处理领域的一个热点问题，是连通个体水平分割和群组水平分割的纽带。简单描述就是基于一定的变换规则实现图像之间的相互映射，数学表示如下：

式中，Ii和Ij表示给定的图像；F( )表示图像的映射函数；m表示变换的相似度测量；配准的目标是通过优化算法在实现m( )最大的基础上找到映射变换函数。

本文选用先进的图像标准化工具ANTs[6]，该工具优于一些传统的配准方法和基于深度学习的配准算法[7]，比如IRTK、AIR、NiftyReg、Elastix和VoxelMorph等，尤其对磁共振图像的配准效果非常优越。通过微分同胚的对称性正则化转换模型可以有效解决配准过程中的拟合性问题，而且基于均方差、互相关和交互信息可以实现多模态条件下的图像配准。

3.1.3 图像特征工程

弥散性纤维束追踪主要包含确定性纤维追踪和概率性纤维追踪两种，可有效提取图像结构和连接信息。通过设置感兴趣脑区，以起始体素作为种子点，沿着主方向以固定的步长向前进行追踪。确定性纤维追踪操作简单且速度快，但是容易受到噪声干扰，当组织出现容积效应或交叉纤维时，效果较差。概率性纤维追踪综合考虑主特征方向和穿过体素点内的纤维方向分布信息，通过计算各个方向上追踪到的纤维束得到概率图，对部分容积效应和不确定噪声有较好的适应性。本文基于每个体素点的流线分布，通过对纤维走向进行多次重复采样来生成体素的连通概率，实现了概率条件下的纤维跟踪特征提取。

3.2 图像分割算法

机器学习聚类算法常用于数据聚类、图像分割或锚框选定等，通过调研最相关的方法应用和大量理论研究[8-11]，本文基于主成分分析(Principal Component Analysis，PCA)算法和非线性最小二乘(Least Squares，LS)算法提出一种无监督学习的确定聚类数选取(Selection of Cluster Number，SCN)算法，算法基本流程如下：

图1 SCN算法基本流程图

SCN算法主要包含三个方面：

(1) 针对所有被试个体，基于特征工程得到感兴趣区每个体素点到全脑之间的连接，通过设计的算法对连接值进行提取并用矩阵表示。为了促进数据存储和加速计算，同时降低数据噪声，对矩阵结果进行下采样，构建感兴趣分割脑区在个体空间水平上的连接矩阵，并基于连接信息进行相关性分析，结果作为聚类分割算法的特征输入。

(2) PCA分析算法的主要思想是基于n维的特征数据，找到一组相互正交的坐标向量，通过映射变换重新构造出正交的k 维特征。为了实现PCA 算法重构映射，通过L2范数最小化原始输入x 和重构向量之间的距离，最终求解映射W，设置损失函数为：

表1 PCA算法基本流程

PCA 三准则包括累积贡献率，特征值和碎石检验。一般情况下，累计贡献率在70%-95%之间；特征值保留大于1；在个体水平上，每一个被试特征数据经空间变换后，基于LS约束提高功率曲线的拟合精度，通过对拐点求平均和离散度阈值化处理最终确定聚类数。

(3) 谱聚类是优秀的无监督学习模型之一，被广泛的应用于脑图像分割。相比于Kmeans 等传统的聚类方法，SC 算法对数据分布的适应性能力较强，更容易捕获到复杂形状的数据结构规律，聚类效果较优。算法的基本流程如表2所示。

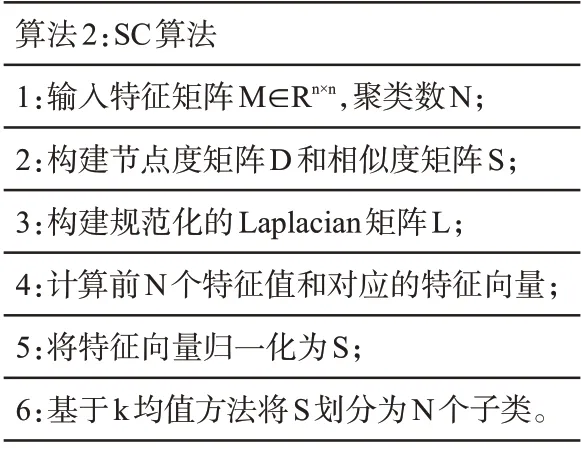
表2 SC算法基本流程

3.3 结果对比验证

3.3.1 组水平概率性图谱

为了进一步验证SCN 算法的合理性，将图像分割结果配准到标准空间，计算组水平上的图像最大概率分割结果，估算图像分割结果的分割模式一致性，并和SCN方法的结果进行对比评估。图像最大概率分割结果数学模型表达如下：

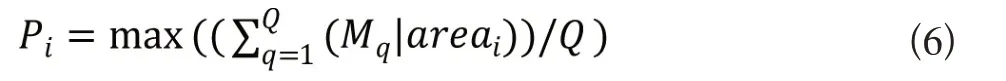
其中，Q表示被试数量，qQ；通过反向配准将个体弥散空间的分割结果转换到得到标准空间的被试Mq的分割结果areai，i表示第i类图像分区。

3.3.2 验证指标

基于克莱姆相关系数[12](Cramer’s V，CV)和拓扑距离指标验证图像分割的一致性，衡量细分区域之间拓扑分布的相似性。

给定r×c的列联表T，克莱姆相关系数的数学计算表达式如下：

式中，φ表示Phi 系数；Tij表示Mp的分区结果所包含的子区areai和Mq的分区结果所包含的子区areaj之间地重叠度，i=1，2，…，r，j=1，2，…，c。CV的取值范围是[0，1]，值越大表示分区模式一致性越好，说明不同个体间分区结果的重合程度大。

对于所有的被试，将左侧和右侧感兴趣区对应的归一化拓扑矩阵进行向量化表示，通过计算余弦距离可以得到拓扑距离指标值TpD。其取值范围是0 到1，值越小则图像分割效果越好。

4 实验结果与分析

4.1 实验设计

本文的实验数据为猕猴脑图像数据[13]，数据采集回波时间(TE)为21．8ms，重复时间(TR)为9800ms，翻转角(FA)为90°，采集矩阵为140×110，视野场为94mm×66mm，图像分辨率为0．6mm×0．6mm×0．6577mm，最大梯度幅值为276mT/m，帧数为64。模板选用美国科学家绘制的INIA19图谱数据[14]，整合图谱的后扣带和扣带峡作为感兴趣区，基于互相关信息进行图像配准；对感兴趣区体素点的连接计算采样流线数为15000，并采用距离校正算法补偿相隔较远的体素点之间连接值；为了降低数据噪声和促进数据存储和计算，下采样各向同性分辨率为2mm×2mm×2mm；个体水平分割时，SCN 算法特征值准则阈值为1，累计贡献率阈值为80%。采用组水平验证指标对个体水平图像分割结果进行交叉验证时，根据先验知识[13]和脑区大小，图像分割最大数值设为12。

4.2 实验结果

通过实验计算，最终感兴趣区图像分割聚类数为4。如图2所示，为不同被试个体水平上左右侧感兴趣区图像分割的特征值和累计贡献率指标结果，其中柱状图表示特征值分布情况，折线图表示累计贡献率的分布情况。在设置的特征值和累计贡献率的阈值规则约束下，分割聚类数为4时满足要求。

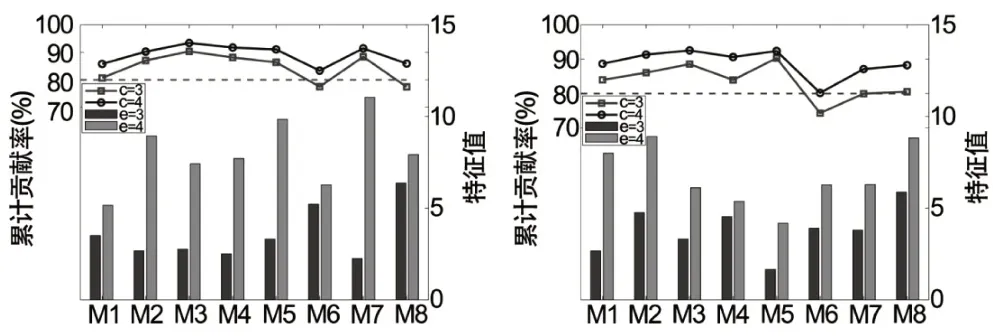
图2 个体水平上特征值和累计贡献率指标

如图3所示，为左右侧感兴趣区图像分割的碎石检验结果图。通过碎石检验，计算所有被试个体的拟合特征曲线的拐点，然后再进行均值化处理，最终综合上述指标确定最终聚类数。由图结果，左侧和右侧的感兴趣区可被分割为4个明显差异特征的精细亚区。

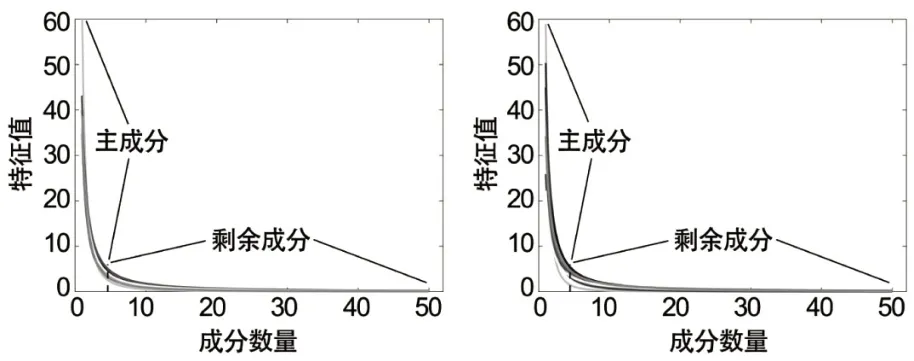
图3 个体水平上碎石检验指标

确定合适的分区聚类数，随后基于机器学习谱聚类算法对所有图像数据进行分区聚类，并在标准空间模板上显示最终的分区结果。如图4所示，为轴状面的不同层选的图像分割结果显示，上方为左侧感兴趣脑区图像分割结果，下方为右侧感兴趣脑区图像分割结果。

图4 轴状面不同层选的图像分割结果

4.3 实验验证分析

为了进一步验证SCN 算法的合理性，在组水平结果上对结果进行实验验证评估。如图5 所示，为基于对半采样法的克莱姆相关系数验证指标。由图通过观察克莱姆相关系数曲线变化趋势，相比于其他分区数目，将感兴趣脑区分为4 个亚区时，分区模式一致性较好且分区结果更精细。此时左侧和右侧感兴趣脑区图像分割的重合度分别为81．86%和74．65%。

图5 克莱姆相关系数指标

如图6 所示，为基于拓扑距离相似性计算的验证指标。一般情况下，对于同一个体的左右脑半球和不同个体之间大脑图像分割的结果具有假定的同源性，即双边大脑在结构上是相似的。由图可知，根据拓扑距离相似性指标曲线变化，将感兴趣脑区图像分割为4个区域时，分割区域之间的拓扑分布比较相似，分区效果较好。

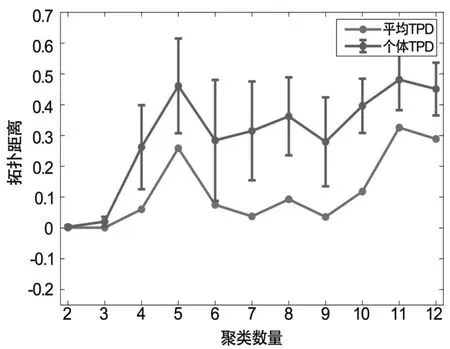
图6 拓扑相似性指标

综上分析，最终聚类数为4，该结果和个体空间水平上确定的分区数目一致。

5 结束语

本文提出了一种基于无监督学习的图像分割算法，通过提取图像的生物特征信息，基于非线性最小二乘法构建主成分分析框架流程确定聚类分割数目，最后利用谱聚类算法实现图像区域分割。通过对猕猴磁共振脑图像的分割实验表明，该算法不仅使图像分割更高效，而且分割结果和其他方法相比具有较好的一致性，具有良好的分割效果。