变截面梁桥车桥耦合振动分析

张佳荣

（中交城市投资控股有限公司 广州 510000）

0 引言

中国地域辽阔、山河众多，随着经济和社会的发展，越来越多的道路交通设施需要进行修建。桥梁作为道路的咽喉，其安全性不容忽视。车辆经过桥面时，会因车辆自身的振动和桥面的不平整对桥梁造成冲击，导致桥梁发生振动，而振动会对桥梁安全带来极大的威胁。当激振频率与桥梁的固有频率接近时会产生共振现象，桥梁就会破裂，甚至发生坍塌而酿成灾害事故。这不仅会造成严重的经济损失，还会危及人民群众的生命安全，因此移动荷载作用下车桥的耦合振动问题成为工程界研究的热点[1-3]。对于等截面均匀梁的车桥耦合动力分析，国内外已有大量的研究[4]，而对于变截面梁，只有少量的数值模拟研究。在当前四通八达的交通网络中，变截面桥梁的应用越来越多，而变截面桥梁受截面变化的影响，其振动特性更为复杂，加之车辆自身振动的影响，使得桥梁安全受到更大的威胁。已有学者对简支梁桥的车桥耦合振动进行了研究[5]，其他边界条件的研究开展较少。因此，本文对两端固结的变截面梁桥车桥耦合振动进行了分析，并研究了部分参数变化对振动的影响，旨在指导实践，促进桥梁振动分析理论的进一步发展。

1 两端固支变截面梁的动力响应

1.1 理论分析

本文所讨论的弹性体都假定为理想的线弹性体，即材料为均匀和各项同性的，且在弹性范围内服从胡克定律。

式中：F为车辆重力，Δx为脉冲函数。

根据相关文献[6-7]，其控制方程为

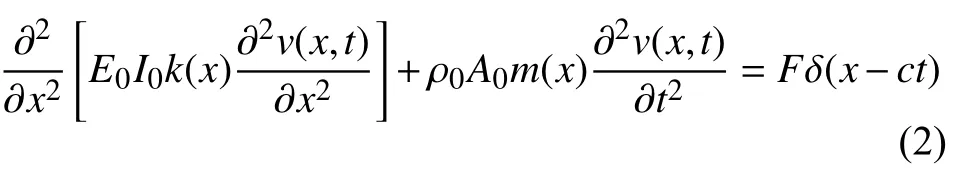
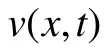
将方程的解分离变量，写作模态函数的线性组合

把式（4）代入式（3），在方程两边同时乘以ϕj，并从0到1积分

根据主质量与主刚度的定义，有

常数c1、c2、c3、c4由系统的边界条件确定。

简谐作用力F具有式（13）的形式：

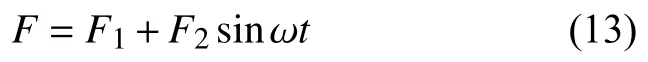
两端固支梁的边界条件为：固定端处梁的挠度v和转角∂v/∂x均等于零。即

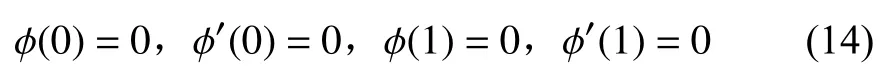
得到关于c1、c2、c3、c4的1个四元一次齐次线性方程组

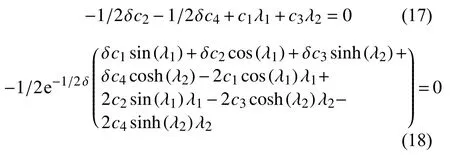
将方程的解c1、c2、c3、c4带入（12）式，得到系统的振动频率方程，经化简得到式（19）

根据已求得的结果，计算M，q（t）：

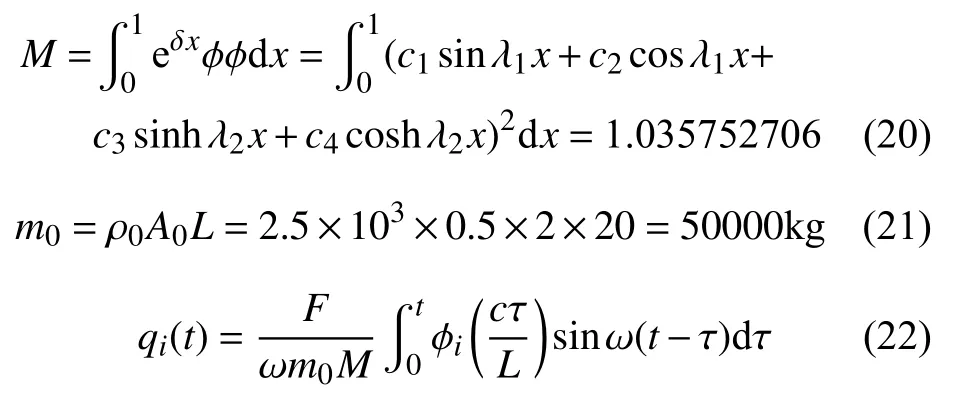
只求解第一阶模态，最后的系统响应方程可以写为

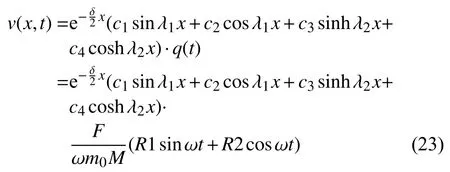
（23）式再加上移动常力作用下梁的响应方程，即可得到力 F1+F2sinωt作用下系统的振动响应方程，如式（24）所示

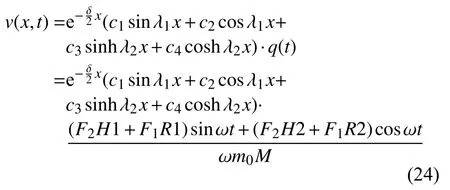
1.2 算例分析与对比

1.2.1 算例分析

某桥梁长20 m，非均匀系数为0.1，杨氏弹性模量为108Pa，密度ρ=2.5×103kg/m3，梁高h=0.5 m，梁初始宽度b0=2 m。车辆以车速c=4 m/s、Δ=0.1、振动频率ω=10工况通过桥梁，运用理论解分析跨中挠度时程曲线（时间归一化）如图1所示。

从图1可以看出，在移动简谐力作用下，桥梁跨中变形先增大后减小，车辆经过桥梁跨中后，挠度达到最大值，之后开始减小，在车辆离开桥面时，跨中挠度出现剧烈振荡。

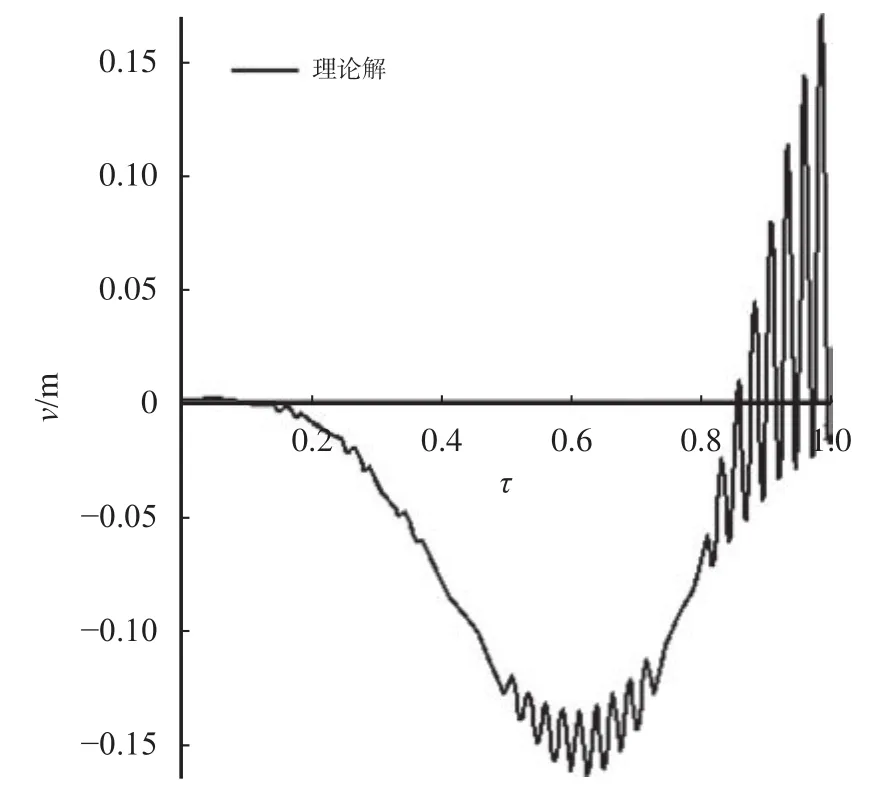
图1 理论解跨中挠度时程曲线

1.2.2 实测值对比

桥梁跨中布设位移计，车辆以c=4 m/s的速度通过桥梁，在桥梁通过的过程中对挠度进行采样，采样频率为2 Hz，实测跨中挠度值分别为：4 mm、13 mm、32 mm、67 mm、131 mm、151 mm、140 mm、73 mm、-2 mm、-71 mm。根据实测挠度值进行挠度时程曲线绘制，将实测值时程曲线时间进行归一化处理，并与理论解挠度曲线进行对比，如图2所示。

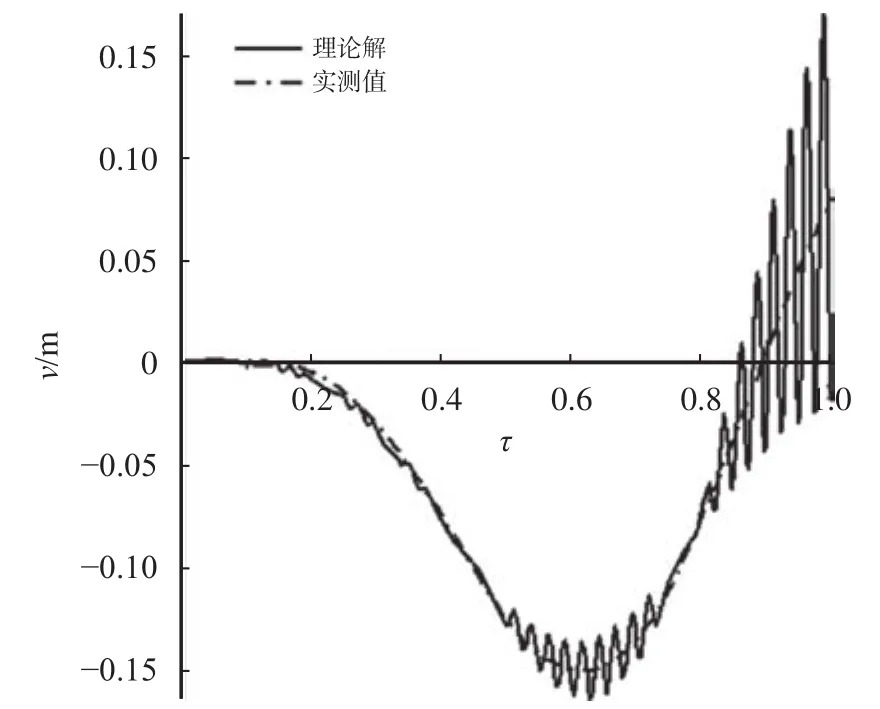
图2 实测值与理论解跨中挠度时程曲线对比

从图2可以看出，理论解与实测值时程曲线基本吻合，说明本文推导的理论解是合理的，可以为相关车桥耦合震动分析提供参考。

2 不同因素对振动的影响

桥梁的振动受很多因素的影响，为此我们选择击振频率和不均匀系数作为变量，研究其对桥梁振动特性的影响。

2.1 改变非均匀系数

保持行车速度和击振频率不变，改变非均匀系数，对桥梁跨中挠度进行分析，时程曲线如图3所示。

图3 两种非均匀系数跨中挠度时程曲线

由图3可以看出，当非均匀系数0.1增大为0.9，桥梁跨中挠度的变化趋势基本不变，在绝对挠度值方面随着非均匀系数的增大，跨中挠度变小。

2.2 改变击振频率

同样保持行车速度和非均匀系数不变，改变击振频率，对桥梁跨中挠度进行分析，时程曲线如图4所示。

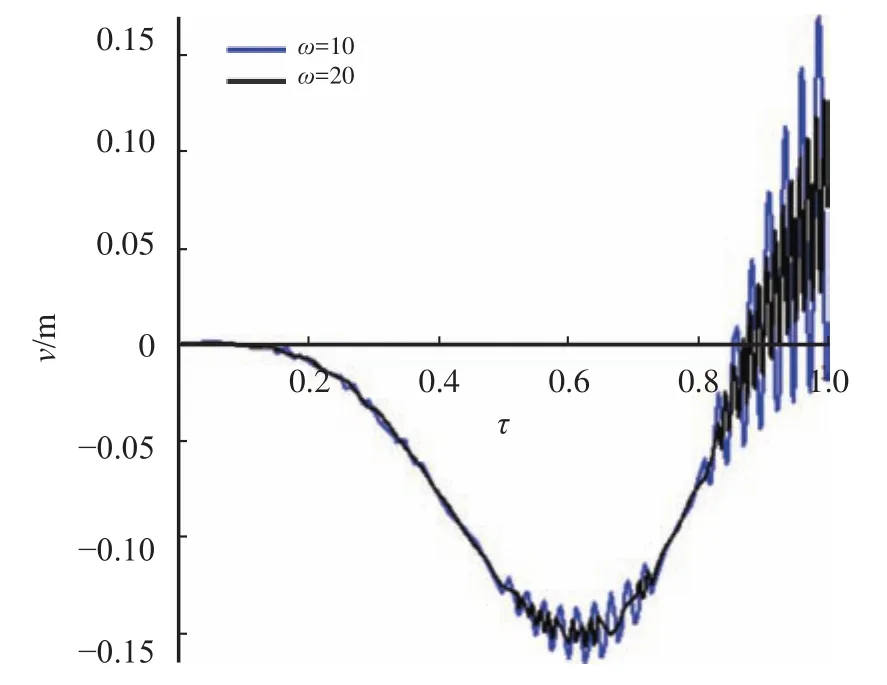
图4 两种击振频率跨中挠度时程曲线

分析图4可知，当击振频率ω由10增加到20，跨中挠度最大值及最大值出现的时间均无明显变化，最大跨中挠度变小。

3 结论

文章运用既有理论对变截面桥梁车桥耦合振动特性进行了分析研究，推导出了振动计算的理论公式，并将理论解与实测值进行了对比。在此基础上，对不同参数变化对振动的影响进行了分析研究，得出如下结论：

1）本文所推导的车桥耦合振动分析理论解公式与实测值相差不大，可以为设计计算提供参考。

2）当桥梁的非均匀系数改变，其他参数不变时，随着非均匀系数的增大，桥梁的跨中挠度变小；当击振频率改变，其他参数不变时，桥梁的振动频率增加。参数的改变对桥梁的振动存在一定的影响，但是对桥梁挠度最大值和最小值出现的时间没有明显影响。