氢燃料电池极板S 型流道结构的仿真优化
刘利娜,饶国燃,张冬洁
(北京理工大学珠海学院工业自动化学院,珠海 519088)
引言
在当前能源和环境问题日益严峻的局面下,氢能作为一种清洁高效的能源材料,逐步受到人们的关注。作为氢能利用的手段之一,质子交换膜燃料电池因具有比功率高、能量转换效率高、操作温度低、耐久性较好等优点而备受青睐[1,2]。在现行商业化的燃料电池设计思路中,膜电极和双极板是组成燃料电池的两大核心组件,其中双极板承担着输送反应气体、排出反应产物、集流、支撑的作用[3]。双极板的流场设计十分重要,合理的流场设计不仅要保证燃料和氧化剂供应充足且分配均匀,还要把反应生成的热和水及时排出,避免发生超温或水淹[4],维持燃料电池正常运行。
有关双极板流场的研究使用较多的有直型流道流场、蛇形流场和交指形流场,研究者一般采用数值模拟方法研究岸宽、流道深度和宽度等形貌尺寸的影响。例如,沈俊等[5]采用Fluent 软件分别研究了在流道中加凸台和扩散层开孔两种方法对强化电池内部传质的效果,得出两种方法均能强化电池内部传质,提高电池性能的结论。Ge[6]等提出了一种二维、稳态燃料电池模型,研究了操作条件、气体流向、膜的厚度等对燃料电池性能的影响,并认为提高阴极压力可改善阳极加湿的问题。Atyabi[7]等新提出了一种新型流场,并采用数值模拟方法将新型流场与传统平直流场进行对比分析,得出了新型流场性能优于传统流场的结论。
本文基于以上研究内容,以S 型流道为研究对象,通过解构S 型流道结构,采用数值模拟方法从全流场层面建立了单流道燃料电池的三维模型,分析了S 型流道主要设计参数对电池性能的影响,同时考虑到阴极是水生成的主要区域,而单电池组装时阴阳极不同对应方式会造成阴极流场结构的不同,故进一步研究了S 型流道对应方式对电池性能的影响,从而为双极板流场结构改进与优化提供参考。
1 模型和方法
1.1 基于FLUENT 的燃料电池物理化学过程建模
质子交换膜燃料电池内部的反应是发生在多体之间的并由多物理场参与的复杂的电化学反应。一个完整的三维全尺寸燃料电池多体模型包括了阳极集流板(AC)、阳极流道(AH)、阳极扩散层(GDL)、阳极催化层(CAT)、质子交换膜(MEM)、阴极催化层(CAT)、阴极扩散层(GDL)、阴极流道(CH)和阴极集流板(CC)等九个部分,其结构示意图如图1 所示。Fluent 软件中的PEMFC 模块可以针对全尺寸燃料电池模型来进行多物理场耦合求解,其中涉及到的控制方程有质量守恒方程,动量守恒方程,能量守恒方程,组分扩散方程,电荷守恒方程和气体扩散方程等[8-10],具体方程如下(1)~(7)所示。通过设置合理的边界条件并耦合求解上述方程就能得到燃料电池内部各组分的分布情况和各反应气体的流动情况。在反应气体流量分配均匀的情况下,极板上每条流道中的反应气体流动、传质与化学反应强度大体相同,为了节约计算成本,本文只选取其中一条流道进行分析。
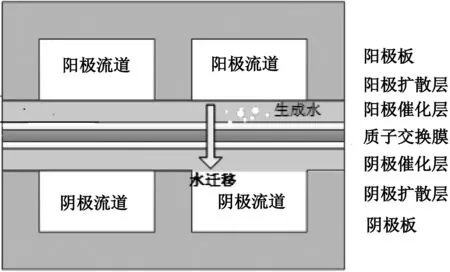
图1 质子交换膜燃料电池的结构示意图
式中:
ρ、ε、P、μ、cp、keff、T、σ 和φ—分别代表密度、孔隙率、压力、粘度、定压比热容、有效热导率、温度、电导率和电势;
Sm、Su、SQ、Sk、Rs和Rm—分别为质量源项、动量源项、能量源项、组分源项、电子电流源项和质子电流源项;
ck、Dkeff、Dk—分别为组分k 的浓度、有效扩散系数和在多孔介质中的扩散系数。
1.2 S 型流道结构
在质子交换膜燃料电池极板流场设计中,直型流道、蛇形流道是两类常见的基本流道型式。前者工质流动阻力小,结构简单,但传质效果相对较差;后者工质流动路径复杂,阻力较大,且在大型极板流场设计中较难应用,但传质和排水效果相对较好。S 型流道结构可看成是直型流道与蛇形流道的一种结合,整体上呈现直通型,比直型流道具有更高的湍流度(一定程度上强化了传质),也比蛇形流道具有较小的流动阻力。此外,在金属双极板流场设计中,S 型流道还易于布置双极板中间的冷却液流动通道,例如本田在其专利中即披露了一款采用S型流道的金属双极板燃料电池结构。本文的研究针对S型流道展开。直型、蛇形和S 型流道的结构示意如图2所示。
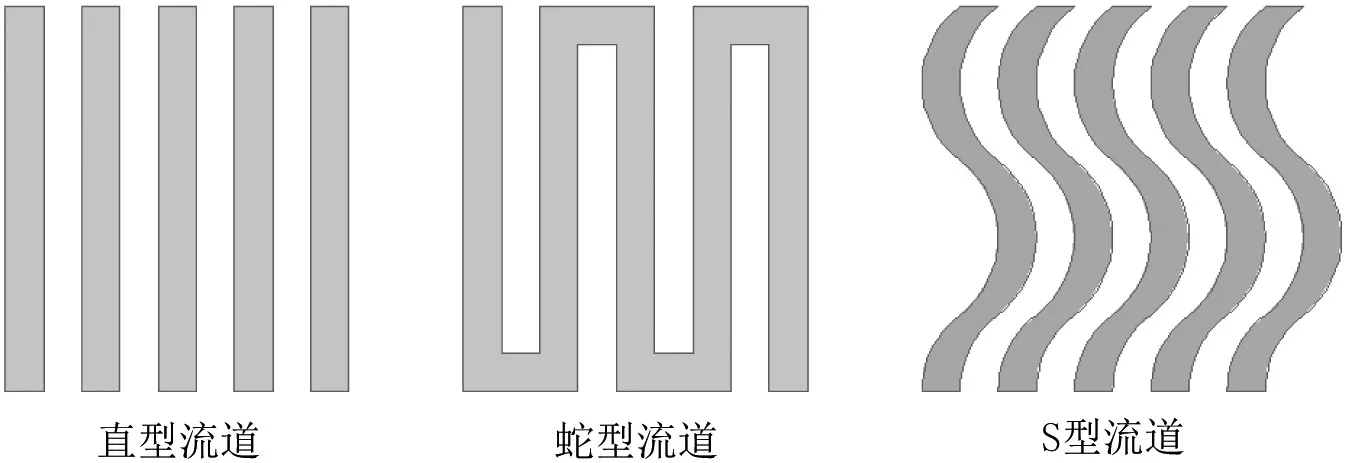
图2 直型、蛇形和S 型极板流道结构
本文将S 型流道结构进行解构,其型线可由三个具有相切关系的圆弧描述,如图3 所示。其中圆A、B 在同一直线上,相距L,且均与圆C 相切(圆A 和B 并不要求相切),三个圆的半径并不要求相同,设其半径分别为R1、R3、R2。将三段相切的弧线平移w 可得到流道宽度为w 的S 型流道。

图3 S 型极板流道型线描述
定义r=d/L 为S 型流道型线的相对弯曲度,其中d 为弯曲度,即为S 型线底部到顶部的距离;L 为拉伸度,即为两个圆心的距离。当R1≠R3时,d 不唯一,故本文仅考虑R1=R3的情形(事实上,R1与R3不同时的S 型流道结构效果处于两种本文所考虑的情形之间,故可忽略),一般要求R1+R2≥L/2,此时,
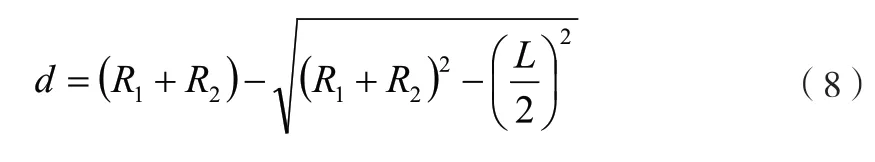
虽然流道的其余参数即流道宽度和深度对流体流动特性和燃料电池性能都存在影响,但已有不少学者进行了研究,本文主要讨论S 型流道拉伸度和弯曲度对工质流动、传质特性和燃料电池性能的影响。在保证流道宽度和深度不变的前提下,通过改变弯曲度和拉伸度的值搭建不同的单流道燃料电池模型来对上述问题进行研究,为了便于模型搭建,假定R1=R2。
除了S 型流道型线之外,本文进一步讨论了燃料电池膜电极两侧阴阳极板上S 型流道的对应方式对燃料电池性能的影响。在保证流道深度、宽度等条件相同的情况下,只改变阴阳极S 型流道的对应方式,建立了两种不同的对应模型,根据阴阳极流道结构相对于膜电极是否对称,将两种模型分别称为正对应模型和反对应模型,如图4 所示。从图中可以看出,两种模型的阳极流道完全相同,而阴极流道弯曲方向相反。本文将通过研究两种模型的单流道燃料电池极化曲线对上述问题进行研究。
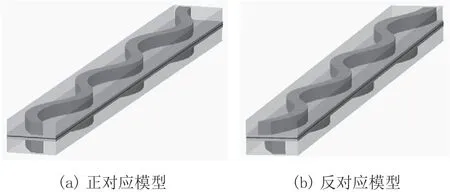
图4 单流道燃料电池几何模型
正反对应模型单流道燃料电池的整体几何尺寸为50 mm(长)×4 mm(宽)×2.66 mm(高),其中膜电极的有效活性面积为50 mm×4 mm,流道截面尺寸为1 mm×1 mm,其余几何尺寸如表1 所示。而进行S 型流道设计参数影响研究时,电池组装方式采用正对应方式建模,且保证流道截面尺寸相同。

表1 单流道燃料电池的几何尺寸
边界条件的设置对燃料电池模型的求解结果非常重要。将阴、阳极进口边界全部设置为质量流量进口,通过改变工作电压来得到不同工况下的电流密度,从而得到燃料电池的极化曲线。出口边界采用压力出口,氢氧进气方式采用逆流,即阴阳极流道内气体流动方向相反。各计算区域材料物性参数保持不变,主要材料和边界条件的设置情况如表2 所示。
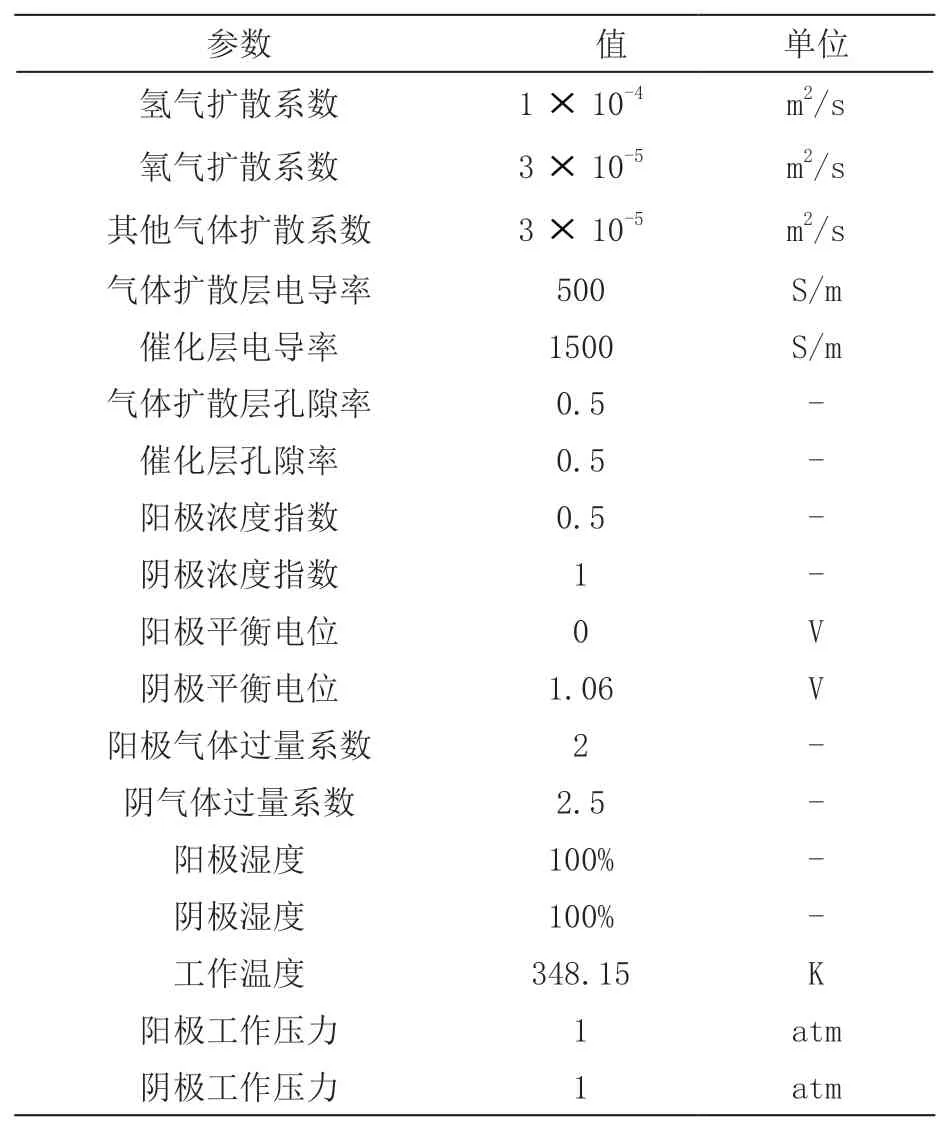
表2 主要材料参数与边界条件
燃料电池的多体模型具有跨尺度的特点,具体表现在其流道长度方向的尺寸和宽深度方向的尺寸一般相差一个数量级,这样给网格的划分和模型的求解带来巨大的困难。为排除网格数量对计算结果的影响,将膜电极中阴极气体扩散层、阴极催化层、质子交换膜、阳极催化层和阳极气体扩散层等五个区域的网格进行细分,并进行独立性验证,使网格数量满足计算要求。求解方法采用SIMPLE 算法,全部方程的求解采用BCGSTAB 方法和F-cycle 循环,并调节松弛因子来加速结果收敛。
2 结果与讨论
2.1 模型验证
为验证模型的准确性和可靠性,将模拟得到的极化曲线与Wei Yuan 的实验数据进行对比[10],如图5 所示。在进行模拟计算时所用各种材料的物性参数、边界条件等均参照文献进行选取和设置,电池的运行工况即操作条件也与实验保持一致。从图中可以看出,模拟结果与实验数据基本吻合,说明模型具有准确性和可靠性,可满足计算要求。
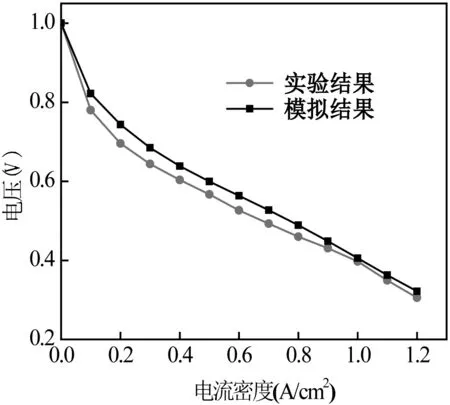
图5 模拟结果与实验数据对比
2.2 S 型流道型线结构的影响
为研究S 型流道拉伸度对燃料电池性能的影响,采用控制变量法保证流道深度、宽度和弯曲度等参数不变,只改变拉伸度可得到六种不同的S 型流道设计方案,如表3 所示。全部采用正向组装方式建立相应的单流道燃料电池模型,在相同工作电压下比较六种方案的电池性能,并与相同条件下直型流道的结果进行对比。

表3 不同拉伸度的设计方案
图6为不同拉伸度对燃料电池性能的对比,从图中可以看出,氧气的流动阻力和单电池的电流随着拉伸度的增加均在减小,阻力的减小程度明显大于电流的变化。同时计算得到了相同条件下直型流道的流动阻力为138 Pa,电流为0.594 A,而方案6 中S 型流道的流动阻力为143 Pa,稍大于直型流道,电流为0.591 A,与直型流道几乎相同,这是因为拉伸度越大相同空间尺寸下可布置的S 型流道单元数目越少,对氧气的流动扰动越小,那么S 型流道越来越接近直型流道,所以其性能也越接近直型流道。
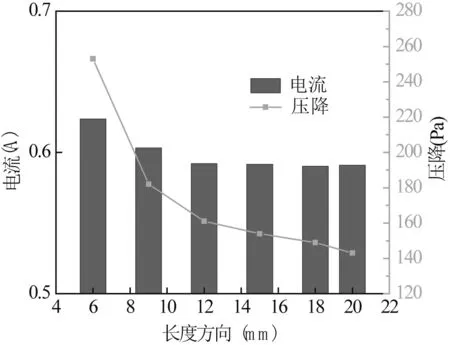
图6 不同拉伸度的对比
类似的,为研究S 型流道弯曲度对燃料电池性能的影响,表4 列出了不同弯曲度的设计方案,其对氧气流动阻力和电池性能的对比如图7 所示,从图中可以看出,弯曲度越大对氧气的流动扰动效果越强,传质效果也越好,氧气的流动阻力也越大,反之,弯曲度越小,流动阻力也越小,那么S 型流道也越接近直型流道。而单电池的电流并没有随着弯曲度的增加一直升高,这是由于扰动效果增强的同时加快了化学反应速率,使得反应生成的水增多,流道越弯曲排水越困难,更容易发生“水淹”,所以电流有所降低。方案10 中S 型流道的电流最大,最大电流为0.992 A,与直型流道相比,电流提升了的0.67倍。
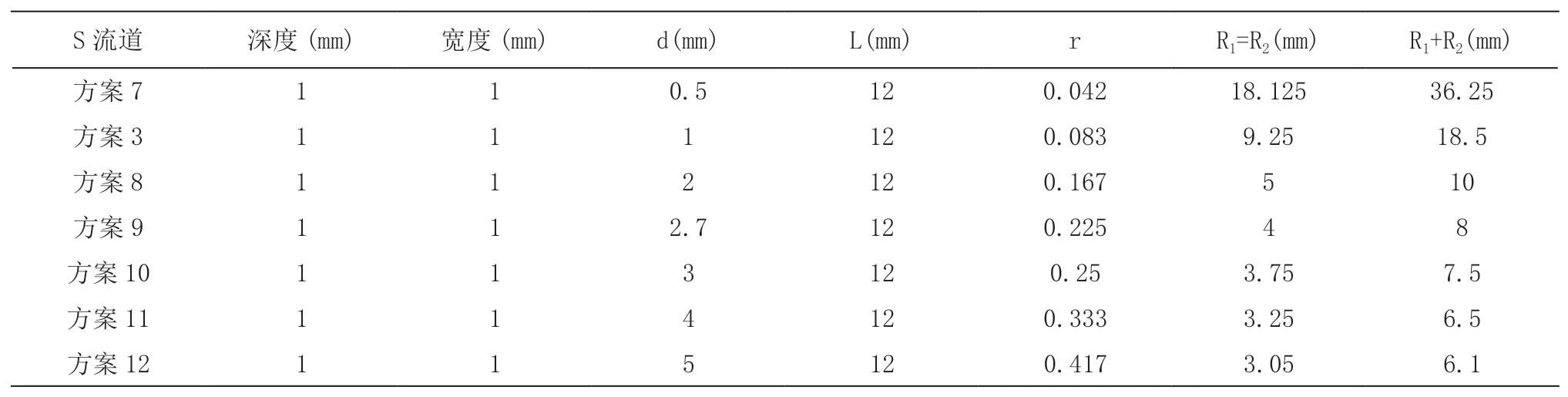
表4 不同弯曲度的设计方案

图7 不同弯曲度的对比
综合比较弯曲度和拉伸度对电池性能的影响作用,可以发现弯曲度对氧气的流动扰动作用较大,传质效果较好,所以单电池的电流较大。而相对弯曲度的大小是由两者共同决定的,单从相对弯曲度分析,流动阻力随着相对弯曲度的增加
单调递增,而单电池的电流随着相对弯曲度的增加先升高后降低,存在一个最优值。特别的对于方案1 和方案8,方案1 的电流为0.624 A,方案8 的电流为0.615 A,虽然两种方案中弯曲度和拉伸度均不相同,可相对弯曲度的大小却是相同的,所以两种方案的电流相差不大。
2.3 阴阳极S 型流道对应方式的影响
正反对应模型单电池的极化曲线如图8 所示。从图中可以看出,电池的电压随着电流密度的升高而逐渐降低,电池的功率密度随着电流密度的升高先有所升高然后降低。在低电流密度下,两者的极化曲线几乎重合,说明两者的性能相差不大,而在高电流密度下,两者的性能有了明显不同,尤其在电流密度大于1 A·cm-2时,反对应模型的电压和功率密度均高于正对应模型,说明在高电流密度下,反对应模型的电池性能优于正对应模型,因此优先采用反对应的方式来组装单电池。这是由于正对应模型阴阳极流道结构关于膜电极相互对称,氢气和氧气与膜电极的公共接触面积相同,同时阴阳极板与膜电极的公共接触面积也完全相同,导致膜电极的总暴露面积较小,而反对应模型,氢氧流道相互交叉,氢气和氧气与膜电极公共接触区域较小,但阴阳极板与膜电极的总暴露面积较大,提高了膜电极的利用率,从而使电池的性能有了提升。

图8 两种模型单电池的极化曲线
3 结论
本文基于S 型流道建立了多种不同的单流道燃料电池三维几何模型,并采用数值模拟方法分别研究了S 型流道主要设计参数和S 型流道对应方式对燃料电池性能的影响,研究表明:
1)S 型流道的弯曲度和拉伸度都会影响燃料电池的性能,与拉伸度的影响作用相比,弯曲度的影响作用较大,两者共同决定了相对弯曲度的大小,一般相对弯曲度越大,流动扰动越大,传质效果越好,流动阻力也越大,同时也会造成排水比较困难电池性能下降,故存在最优的相对弯曲度值,使得流道在流动阻力和传质效果上达到平衡。
2)通过对比正反对应模型的极化曲线可以发现,在高电流密度下,反对应模型膜电极的利用率有所提升,使得其单电池的性能优于正对应模型。因此,在单电池组装时,优先选用反对应方式。

