几何参数对矩形薄壁蜂窝网格高桥墩稳定性的研究
许琼方,薛 江
(天津城建大学 土木工程学院,天津 300384)
交通建设用地开发是土地利用最重要的内容之一,随着我国西部地区的开发工作逐渐展开,山区桥梁日益增多,跨山跨河桥梁的建设不可避免,高墩高架桥成为山区桥梁建设的主要类型[1].当桥墩高度超过40 m时,实体墩明显已经不适应设计要求,空心薄壁高墩形式应运而生,本文针对高架桥发展提出一种新型高墩结构——矩形薄壁蜂窝网格高桥墩.
矩形薄壁蜂窝网格高桥墩是一种由蜂窝夹层结构发展而来的空心薄壁结构,桥墩墩壁是由钢筋混凝土构成的曲面薄壁结构,桥墩内部是由多块矩形薄板连接形成的四边形蜂窝结构.蜂窝夹层结构由上下面板和蜂窝芯层组成,上下面板被中间芯层隔开使其具有高比刚度和比强度的同时,还比非夹层结构具有更轻的自重[2-4].国内外对蜂窝夹层结构的研究和应用大多在航天航空领域,王宝芹[5]、杜正兴[6]、唐俊[7]等采用有限元模型和工程方法分析计算以及试验手段对复合材料蜂窝夹层结构的总体稳定性进行了研究,并指出了夹层板总体铺设为对称时,可忽略面板耦合刚度对临界载荷带来的影响.张铁亮等[8-9]建立考虑芯层几何特征的有限元模型进行屈曲分析,并研究了芯层几何参数对结构稳定性的影响.杨相展[10]、杨建林等人[11]从线性屈曲和非线性弹塑性屈曲两方面对空心薄壁高墩稳定性进行了分析,并通过对不同壁厚桥墩的一阶屈曲模态与特征值的分析,给出了局部失稳与整体失稳的临界条件.段志岳[12]提出增加横系梁和材料强度对空心薄壁高墩稳定性有利,但提高幅度不大,增加壁厚可以提高全桥的稳定性,但同时增加了材料的用量,增大墩身截面刚度,不利于箱梁的受力和变形,故壁厚选择需控制在合理区间内.
由于蜂窝芯层的高度几何复杂性,既有研究大多研究横隔板对空心薄壁高墩局部失稳的影响[13-14],对多网格空心薄壁高墩稳定性研究较少.本文采用相同材料的加劲板来替代蜂窝芯层,使其在提高桥墩的整体刚度和稳定性的同时也具有更简单的结构形式,并基于桥墩网格几何参数对矩形薄壁蜂窝网格高桥墩稳定性的影响规律做一系列研究.
1 结构稳定原理
1.1 线性屈曲理论
结构线性屈曲分析即特征值屈曲分析,在结构平衡稳定状态,假定结构线性,根据最小势能原理,得到结构临界平衡状态平衡方程
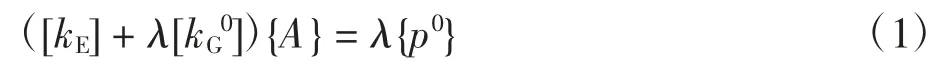
在任一微小扰动后,结构进入另一平衡状态,此时结构承载力不变,方程转化为求刚度矩阵特征值问题

结构i阶临界荷载

式中:[kE]为结构线弹性刚度矩阵;[kG]为结构初始刚度矩阵;{A}为节点位移量;{p0}为结构所受外荷载;λi为结构i阶特征值,即结构第i阶屈曲系数;δi为对应于的特征向量.
1.2 能量变分原理
由能量变分原理可知,在稳定问题中,临界荷载应使结构总势能(即外力势能K与内力势能U之和)取极值.以双薄壁空心墩为例(见图1),桥墩外框尺寸A×B,墩高H.
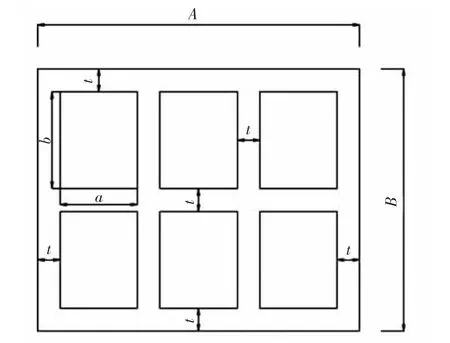
图1 双薄壁空心墩截面示意图
以纵桥向为x轴,横桥向为y轴,竖向为z轴,桥墩空心网格排列形式m×n,则内力势能U和外力势能K为:

式中:ω为结构挠曲函数;D为结构抗弯刚度,D=EI;E为材料弹性模量;I为结构惯性矩.
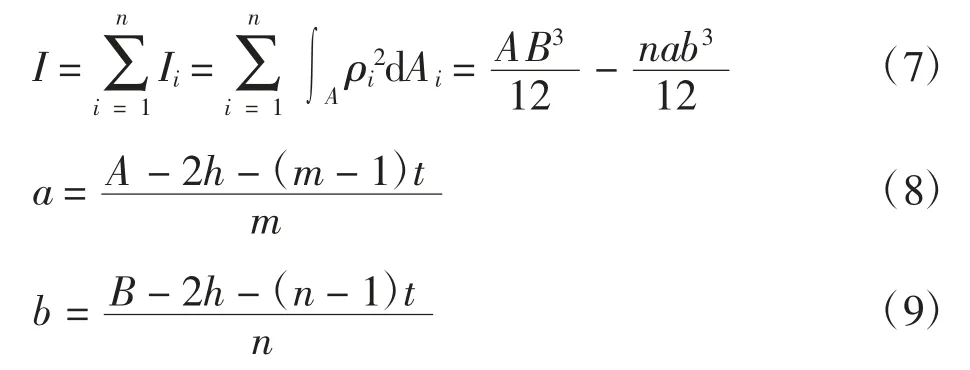
式(5)-(9)可得结构临界荷载

2 算例分析
某矩形双薄壁空心墩,桥梁全长76 m,主墩外框尺寸A×B=10 m×8 m,墩高H=100 m,a=3.8 m,b=6.4 m,h=t=0.8 m,截面面积S=31.36 m2结构模型示意图如图2所示.
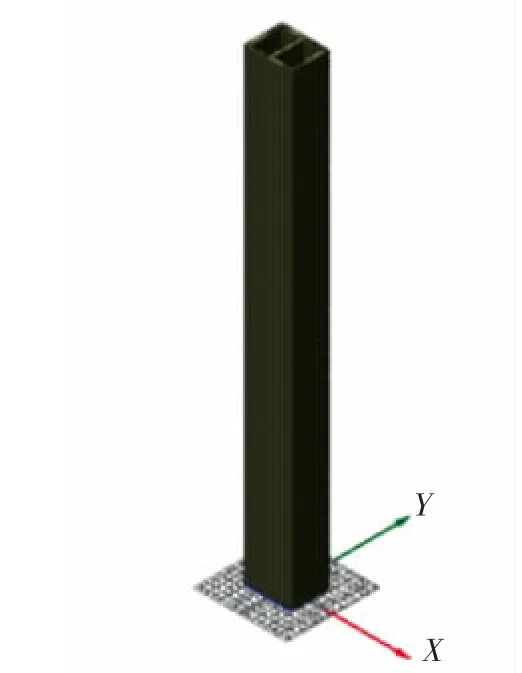
图2 矩形双薄壁空心墩模型图
模型初始设定轴压荷载
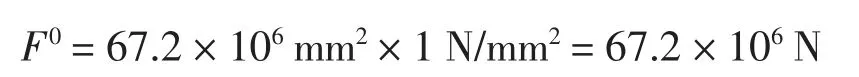
均布轴压荷载

桥墩模型屈曲系数
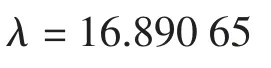
临界荷载
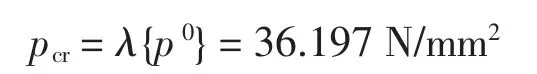
对以上桥墩模型墩柱壁厚、网格壁厚、空心网格数量和网格排列形式等几项几何参数进行改变后再次建模分析,屈曲系数变化见表1-4.
由表1-4可知,桥墩屈曲系数随其墩柱壁厚、网格壁厚、空心网格数量和网格排列形式的改变会产生不同程度的变化,下文将对其具体变化规律进行研究.
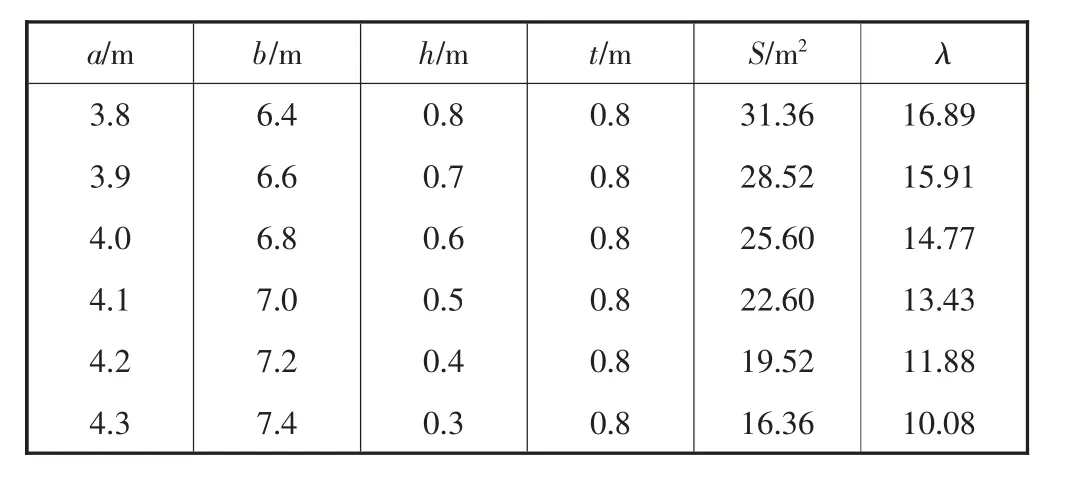
表1 桥墩墩柱壁厚变化参数表
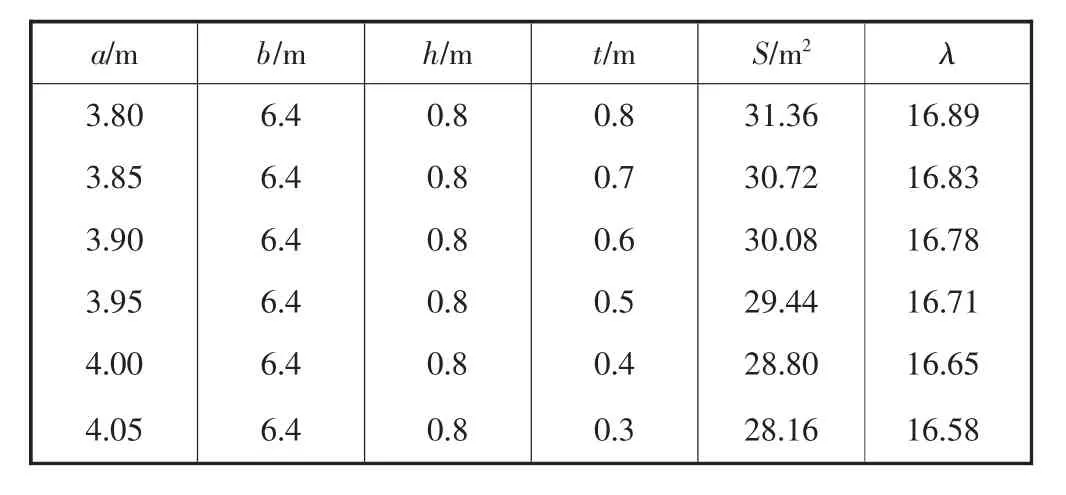
表2 桥墩网格厚度变化参数表
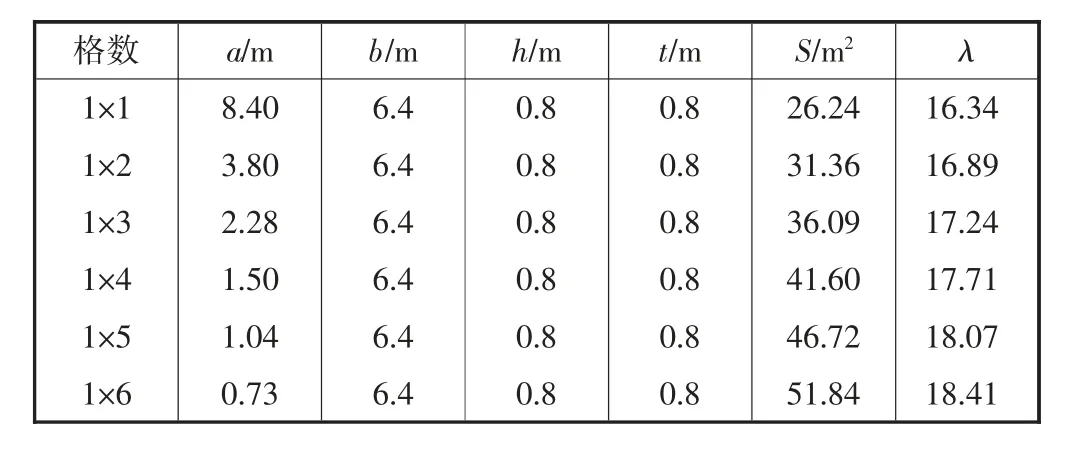
表3 桥墩网格数量变化参数表
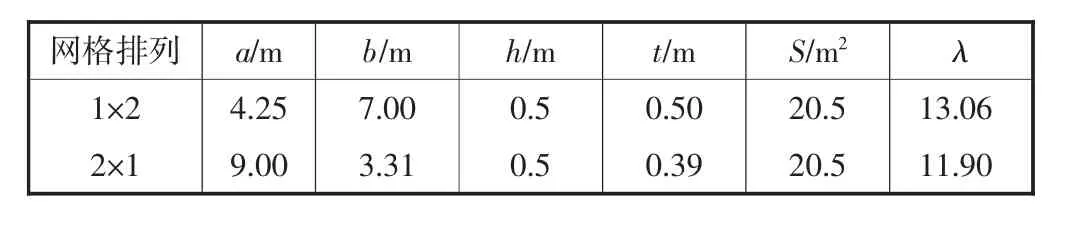
表4 桥墩网格排列变化参数表
3 网格不同排列形式下桥墩截面面积及高度的影响
3.1 桥墩截面面积的影响
以算例为研究对象,不改变桥墩外轮廓尺寸和形状,调整矩形网格的数量、位置和面积,建立模型分析不同网格类型下,桥墩截面面积对稳定性的影响.模型按照网格数量和排列形式分为14组(见图3),图3c中2×3表示桥墩截面网格排列形式为2排3列共6个网格布置.模型计算结果见图4.
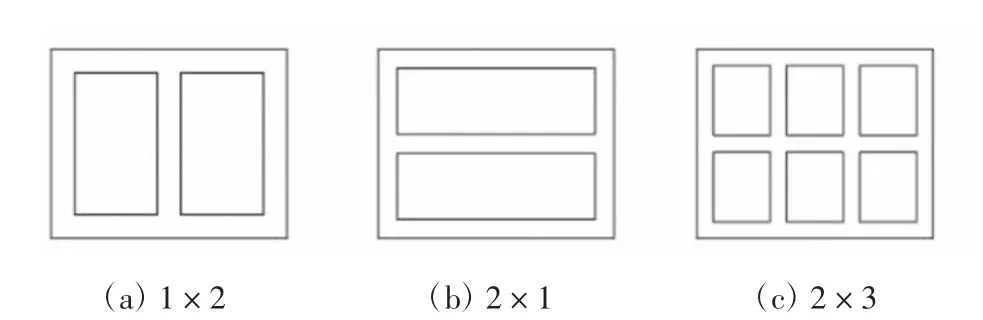
图3 桥墩网格布置形式示意图
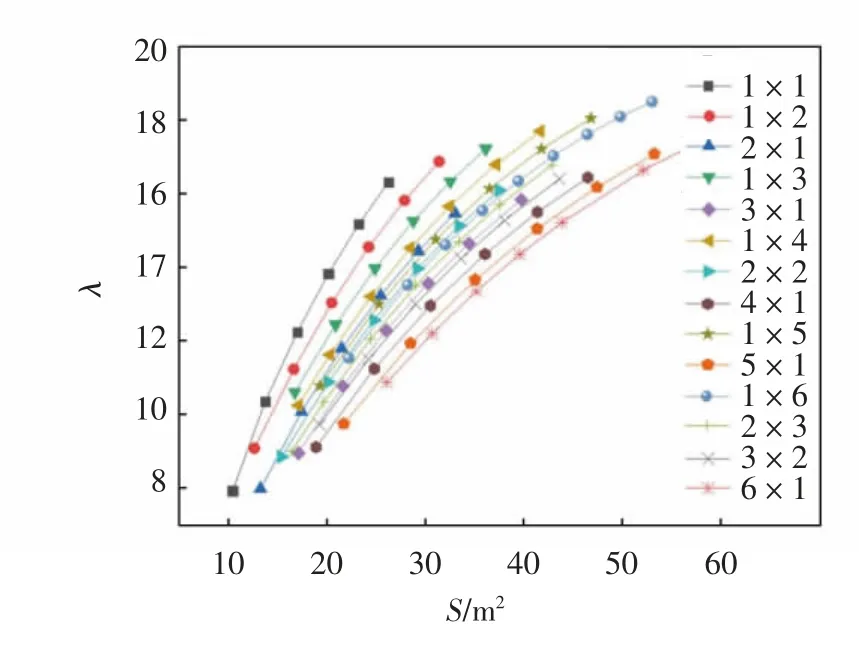
图4 桥墩S-λ图
通过对图4的分析,可以得出以下结论:
(1)曲线图整体呈“扇形”分布,随桥墩截面积增大,桥墩截面网格数量和网格排列形式对桥墩稳定性的影响逐渐增大.
(2)矩形薄壁蜂窝网格高桥墩屈曲系数随桥墩截面面积增大呈凸形抛物线形增加趋势.相同网格数量和排列形式下,随桥墩截面面积增加,桥墩自重的增大对稳定性的降低趋势增大,但截面惯性矩的增大对其稳定性的提高始终大于自重增大对桥墩稳定性的降低.
(3)随网格数量增加,结构S-λ曲线斜率减小,曲线位置聚集.相同网格形式和截面面积情况下,网格数量增加对截面惯性矩的减小呈下降趋势.
(4)网格数量越多,桥墩屈曲系数上限越高,即桥墩可通过改变其他参数来提高稳定性的空间越大.
(5)随着网格排列形式由横向单排转变为多排,桥墩惯性矩减小,屈曲系数减小,因此,横向“一”字型排列为矩形薄壁蜂窝网格高桥墩网格最佳排列形式.
3.2 桥墩高度的影响
以算例为研究对象,通过调整矩形网格的数量、位置和桥墩高度,分析不同网格类型下,桥墩高度对稳定性的影响,计算结果见图5.
网格数量1~6的桥墩模型截面面积分别为:S1=17 m2、S2=20.5 m2、S3=26 m2、S4=24.75 m2、S5=31 m2、S6=29 m2.
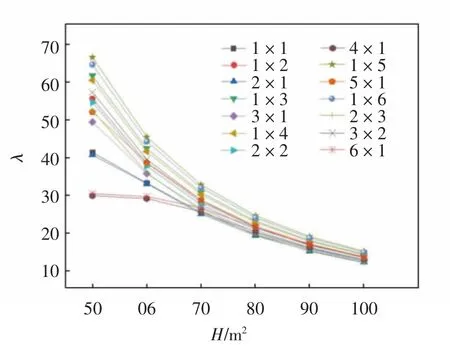
图5 桥墩H-λ图
通过对图5的分析,可以得出以下结论:
(1)矩形薄壁蜂窝网格高桥墩,墩高变化区间为50~100 m时,桥墩曲线整体呈现“喇叭”状,即桥墩高度越大时,桥墩H-λ截面惯性矩和桥墩自重对其稳定性的影响越小.
(2)矩形薄壁蜂窝网格高桥墩屈曲系数随桥墩高度的增加而减小,同时曲线呈凹形抛物线形状,先迅速减小,然后逐渐趋于平缓.
(3)同等网格数量和截面面积的矩形薄壁蜂窝网格高桥墩,网格“一”字型排列时,结构最不容易失稳.
(4)在桥墩网格排列形式为4×1和6×1时,桥墩截面各几何参数对其稳定性的影响规律出现变化,曲线出现拐点,前半段形状变为凸形.相同网格排列形式下,桥墩网格数量大于5后,截面空心率增加对惯性矩的提高开始低于桥墩自重增加、墩柱壁厚和网格厚度减小对截面惯性矩的减小,因此桥墩稳定性发生突降;在相同网格数量下,由桥墩网格排列形式从横向单排转变为多排引起的截面惯性矩减小趋势与截面空心率成正相关,因此,桥墩屈曲系数在截面面积相邻的模型组中,在空心率差值最大的S5和S4之间产生最大下降值.
(5)桥墩网格数量从1增加到6时,其截面面积整体呈逐渐增加趋势,其中网格数量由3格增加到4格时和5格增加到6格时,后者截面面积较前者略微减小,由此时曲线变化可知:相同网格排列形式下,桥墩网格数量小于5时,各几何参数对桥墩稳定性的影响大小排序为:桥墩高度>截面空心率>墩柱壁厚和网格厚度;桥墩网格数量大于5后,排序变为:桥墩高度>墩柱壁厚和网格厚度>截面空心率.
4 桥墩墩柱壁厚和网格壁厚的影响
以算例为研究对象,将网格排列形式固定为横向“一”字型排列,调整矩形网格的数量、墩柱壁厚和网格壁厚,分析不同网格数量下,桥墩墩柱壁厚和网格壁厚对稳定性的影响,计算结果见图6所示.
通过对图6分析,可以得出以下结论:
(1)桥墩墩柱壁厚与网格壁厚相等时,桥墩空心率的增加与网格数量的增加成正比,网格数量越多,结构稳定性越好.故不同网格数量的桥墩h(t)-λ曲线基本平行分布,桥墩墩柱壁厚和网格厚度对不同网格数量的桥墩稳定性影响规律基本相同.同时,桥墩h(t)-λ曲线均呈凸形抛物线上升趋势,随桥墩墩柱壁厚和网格厚度增加,其对桥墩稳定性的影响逐渐减小.
(2)随桥墩墩柱壁厚增大,不同墩柱壁厚和网格壁厚比值的高桥墩一阶屈曲系数均呈凸形抛物线形增大趋势,当桥墩墩柱壁厚和网格厚度大于墩宽的1/70后,其增大引起的截面惯性矩增大对桥墩稳定性的提高与自重增大对桥墩稳定性的减小逐渐趋于平衡.
(3)随桥墩网格数量增多,曲线变化上限由16.89增加到18.43,可知网格数量越多,结构稳定性上限越高,但影响不大,故应该控制网格数量的增加.
(4)桥墩h-λ曲线图整体均呈“扇形”收拢分布,即相同网格数量下,随桥墩墩柱壁厚增大,由网格厚度增加导致的桥墩稳定性的提高呈下降趋势.
(5)网格数量越多,网格厚度为300 mm到800 mm区间内的桥墩h-λ曲线越分散.即相同桥墩墩柱壁厚下,由网格厚度增大对桥墩稳定性的提高随网格数量增加呈上升趋势.
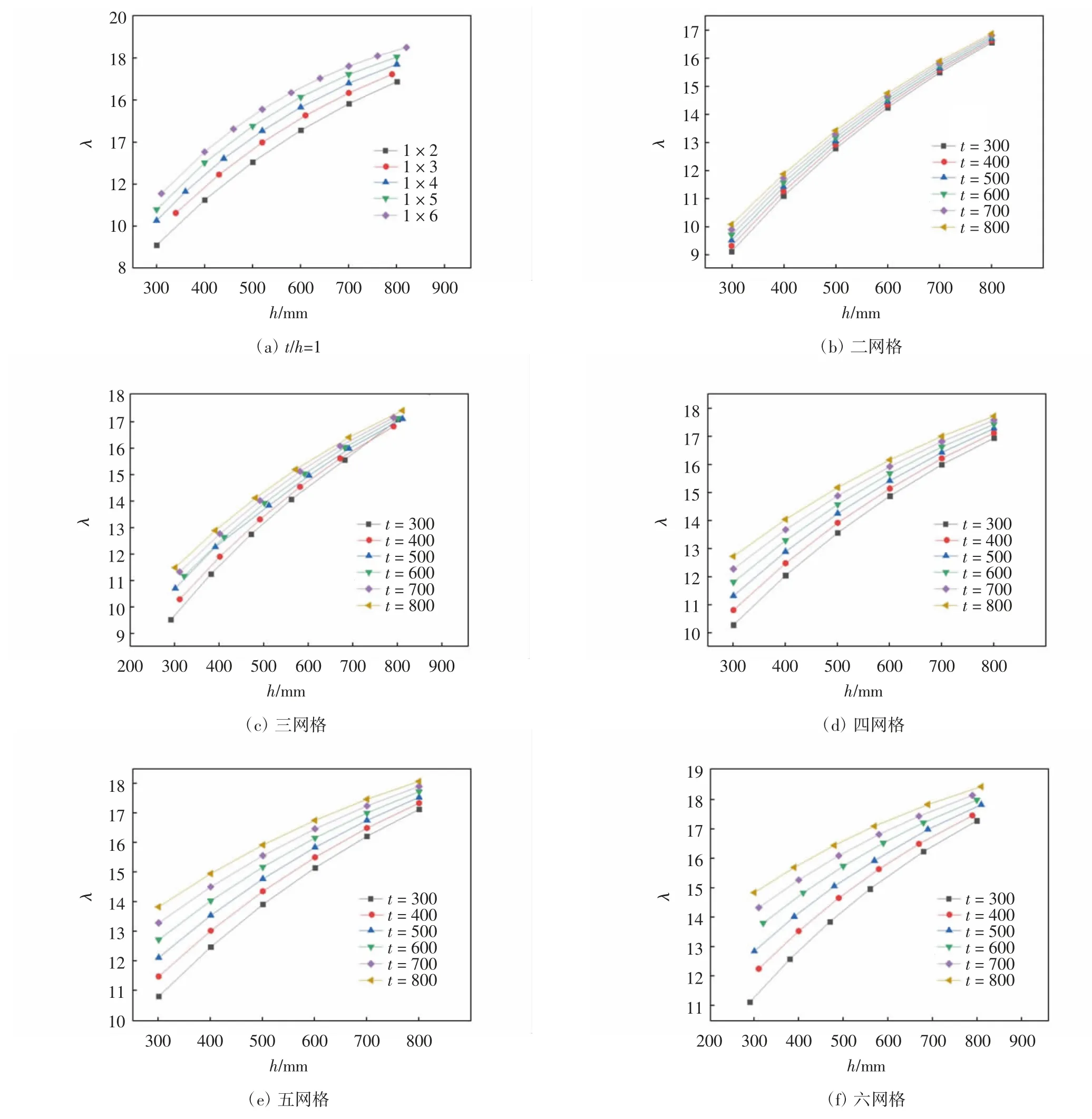
图6 桥墩的h-λ图
5 结论
通过对矩形薄壁蜂窝网格高桥墩结构的设计与建模,并基于结构稳定原理进行的特征值屈曲分析,研究了网格排列形式、墩柱壁厚、网格壁厚和网格数量等主要几何参数对高桥墩稳定性的影响规律,得出以下结论:
(1)在桥墩设计时,可通过增加网格数量、墩柱壁厚和网格厚度来增加桥墩截面惯性矩,从而提高桥墩稳定性,但其对结构稳定性的影响都呈抛物线形变化趋势,在增加到一定程度后,对桥墩稳定性的影响都不再明显.故在此类结构设计时应将桥墩网格数量、墩柱壁厚和网格厚度控制在合理范围内.
(2)当桥墩截面形式对称布置,截面面积和网格数量固定时,减少截面网格列数有利于提高截面惯性矩,从而提高桥墩稳定性.因此,横向“一”字型排列为矩形薄壁蜂窝网格高桥墩网格的最优排列形式.
(3)桥墩截面面积较小时,网格数量和网格排列形式对其稳定性影响较小,随桥墩截面面积逐渐增大,桥墩网格数量和排列形式对其稳定性的影响也逐渐增大.
(4)矩形薄壁蜂窝网格高桥墩墩柱壁厚、网格厚度和网格数量都较小时,其对桥墩稳定性的提高趋势依次减小,因此,在此类桥墩结构设计时,应按照增加桥墩墩柱壁厚>网格厚度>网格数量的顺序采取措施来提高桥墩稳定性.

