一种新的混合粒子群优化算法

徐生兵 蹇柯 夏文杰

摘  要：针对粒子群算法在进化后期收敛精度低、收敛速度慢，尤其是高维时候容易早熟等问题，提出了一种新的混合粒子群优化算法。新算法首先设计了一种新的惯性权重，使惯性权重取值在进化初期和后期都较为适中;其次，为了有效抑制粒子陷入局部极值，引入了粒子最优速度和最差适应值的概念，并以此为基础，设计了粒子的一种新的自适应变异方式;最后引入了平均收敛率和最小平均收敛代数两个概念，可以更好地评价和比较本文算法的性能。八个标准测试函数在100 维、200 维进行的数值实验证实，新算法收敛精度高，收敛速度快，且有效预防了早熟现象。

关键词：粒子群优化;惯性权重;早熟;变异

中图分类号：TP183     文献标识码：A

Algorithm of a New Hybrid Particle Swarm Optimization

XU Shengbing， JIAN Ke， XIA Wenjie

（School of Computer and Information， City College of Dongguan， Dongguan 523419， China）

xusb@ccdgut.edu.cn; jianke@ccdgut.edu.cn; xiawj@ccdgut.edu.cn

Abstract： This paper proposes a new hybrid particle swarm optimization algorithm to solve the problems of low convergence accuracy， slow convergence speed of particle swarm optimization algorithm in the late evolution stage， and being prone to mature early especially in the high-dimensional case. The new algorithm first proposes to design a new inertia weight， which makes the value selection of inertia weight moderate in the early and late evolution. Secondly， in order to effectively restrain the particles from falling into the local extreme value， the concepts of particle optimal velocity and the worst fitness of particles are introduced. Based on this， a new adaptive mutation method of particles is designed. Finally， the concepts of average convergence rate minimum average convergence algebra are introduced， which can better evaluate and compare the performance of the proposed algorithm. The numerical experiments of 8 standard test functions in 100 and 200 dimensions verify that the new algorithm has high convergence accuracy， fast convergence speed， and effectively prevents premature phenomenon.

Keywords： particle swarm optimization; inertia weight; premature; mutation

1   引言（Introduction）

粒子群优化（PSO）算法是由Eberhart、Kenned于1995 年提出的一种基于种群智能行为的优化算法。由于其概念明确、需要设置的参数少、编程易于实现等优点，目前在工程领域已经得到广泛的应用。但PSO算法在优化复杂函数问题时极易陷入局部极值，并且会出现早熟现象，这又限制了其进一步应用。为提高PSO算法的优化性能，许多学者提出了各种改进的PSO算法[1-10]。其中，在惯性权重方面，SHI等人[1]于1998 年首次引入了惯性权重的概念，并提出了一种线性递减的权重策略（LDWPSO）;黄轩等人[2]提出了一种基于随机惯量权重的快速PSO算法（Faster PSO with Random inertia weight，FRPSO），即惯性权重在0.4—0.6的随机取值;LIANG等人[3]提出了一种利用种群质心和种群个体极值质心的PSO算法（PSO with Centroid，CPSO），使得粒子的更新不仅与传统PSO算法中的个体极值和全局极值相关，而且还与种群中其他粒子的位置和个体极值相关。

2  标准粒子群算法（Standard particle swarm optimization algorithm ）

標准粒子群算法的数学描述过程如下：

在d 维搜索空间中，PSO算法首先初始化s 个随机粒子，然后通过追踪两个极值（全局极值和个体极值）位置对粒子的位置进行更新，迭代运行直至满足停机条件，最后输出最优解。其中，在第t 代时，假设某个粒子的位置为，速度为，则第 代粒子的位置和速度分别为：

（1）                                 （2）

其中，式（1）、式（2）分别称为速度更新方程和位置更新方程;称为惯性权重，表示对前一代速度的保留程度，一般取值范围为;c1、c2称为学习因子，一般取值为2.0;是之间均匀分布的随机数;为粒子自身迄今为止找到的最好位置，即粒子的个体极值位置;为整个种群迄今为止找到的最好位置，即种群的全局极值位置。

上述的惯性权重是PSO算法的一个十分重要的参数。SHI等人通过大量的数值实验表明：较大的惯性权重有利于全局搜索，而较小的惯性权重有利于局部搜索，因而可以在迭代初期设置一个较大的惯性权重，以便较为迅速地定位到一个较优的搜索区域;在迭代后期使用一个较小的惯性权重，以便在这个较优的区域进行局部搜索，进而搜索到更好的解。因此，SHI提出了一种惯性权重线性递减（Linear-Decreased Weight， LDW）的策略，即：

（3）

其中，为最大惯性权重，为最小惯性权重，一般取，;为当前迭代次数;为总迭代次数。这样，就会随着迭代次数的增加而线性递减。因此，使用式（3）权重策略的PSO算法被称为惯性权重线性递减的PSO算法，即LDWPSO算法。

3  一种新的混合粒子群优化算法（A new hybrid particle swarm optimization algorithm， NHPSO）

3.1   一种新的惯性权重策略

由于惯性权重在PSO算法中可以控制算法的全局搜索能力和局部搜索能力，因此，关于惯性权重的研究已经取得了不少的进展[2，9]，其中文献[2]经过大量数值实验证实：惯性权重在0.4—0.6随机取值时，其总体实验效果要优于LDWPSO。与LDWPSO的惯性权重相比，FRPSO的特点是：初期惯性权重较小，后期惯性权重较大。但后期惯性权重较大是不利于粒子局部搜索的（这在文献[7]FRPSO与LDWPSO的对比实验中也可以看出来）。考虑到两种权重的各自特点和实验效果，本文构造了一种新的惯性权重，使其值在初期和后期均介于两者之间，具体如下：

（4）

其中，，。

是一个变化范围较小的惯性权重，其变化范围约为[0.1，0.37]，且在迭代后期权重稍有回升;是一个非线性递减的权重，其变化范围约为[0.14，0.9]，这样的变化范围约为[0.15，0.67]。因此，与LDWPSO中的惯性权重相比，新惯性权重初期较小，后期稍大;与FRPSO惯性权重相比，新惯性权重初期稍大，后期较小，符合设计的初衷。三种权重的变化如图1所示（以为例）。

3.2   一种新的变异策略

PSO算法在陷入局部极值的时候，粒子之间的差异性很小，因此，让部分粒子变异将使得算法有机会搜索到更好的解。本文利用粒子的速度信息和种群适应值的信息，构造了一种新的粒子位置的变异策略。为了叙述方便，先对粒子最优速度和最差适应值做如下定义：

定义1：PSO算法中，某个粒子在第代的最优速度

，表示粒子的初始速度。

定义2：PSO算法中，某个粒子在第代的最差适应值

，表示粒子的初始适应值。

那么，对粒子的变异操作是：

（5）

其中，表示粒子在第代的适应值;表示全局极值粒子的最优速度，表示整个种群的当前最优适应值，用来给一个速度扰动。由于是一个较大的数，因此粒子可以以很大概率远离当前位置。选取哪些粒子变异也是提高PSO算法性能的关键，本文变异的准则如下：

设种群在第 代各粒子的适应值分别为，则第 代种群的平均适应值，粒子与绝对偏差，检验值。其中，为粒子的个体极值，为粒子个数。对每个需要进行变异粒子的选取准则是。为了有效防止粒子陷入局部极值和确保算法的稳定性，在每一次迭代中对每一个满足准则且不是全局极值的粒子按式（5）进行变异操作。

3.3   NHPSO算法流程

NHPSO算法的计算流程与LDWPSO算法的计算流程基本一致，不同之处有：（1）需要计算初始化粒子的最优速度和最差适应值，在每次更新的时候也要更新粒子的最优速度和最差适应值;（2）在每一次迭代过程中，对满足变异条件的粒子均要进行变异操作。NHPSO算法的计算流程图如图2所示。

4   数值仿真实验（Numerical simulation experiments）

4.1   标准测试函数

在数值仿真实验中，选取如表1所示的八个标准测试函数对LDWPSO、FRPSO、CPSO和NHPSO进行性能对比实验。

上述测试函数的理论全局最优解均为0。其中，容易优化;低维容易优化，高维很难优化;的优化难度较大;优化难度最大，是典型的极难优化非凸病态函数，是带有一定欺骗性的函数，因为全局最优与最好的局部最优相距很远，因此搜索算法往往朝着错误的方向收敛，是一个最小化问题，一般的PSO算法极易陷入局部极值且极难优化。

4.2   实验参数设置及实验方案设计

4.2.1   實验参数设置

在实验中，所有算法的公共参数设置为：，为搜索区间长度的0.1，粒子的初始化区间为如表1所示的搜索区间，但的初始区间为[-300，300]。LDWPSO算法中，，;FRPSO和CPSO的参数设置均按参考文献设置，且算法优化性能也与参考文献一致。

4.2.2   实验方案设计

为了叙述方便，先给出算法平均收敛率和平均最小收敛代数的定义。

定义3：如果算法在指定代的运算中，最终优化结果，其中为预设精度，则称该次算法收敛。若算法在次运算中，有次收敛，则平均收敛率。

定义4：当算法收敛时，第一次满足预设精度的迭代次数称为该次算法的最小收敛代数;如果算法在 次运算中不收敛，则。设算法在 次运算中，最小收敛代数分

别为，则最小平均收敛代数。

实验方案1：在固定和的条件下，比较。该方案中，，，，如表1所示，实验结果如表2（其中在表2中分别用Ⅰ、Ⅱ表示）所示。

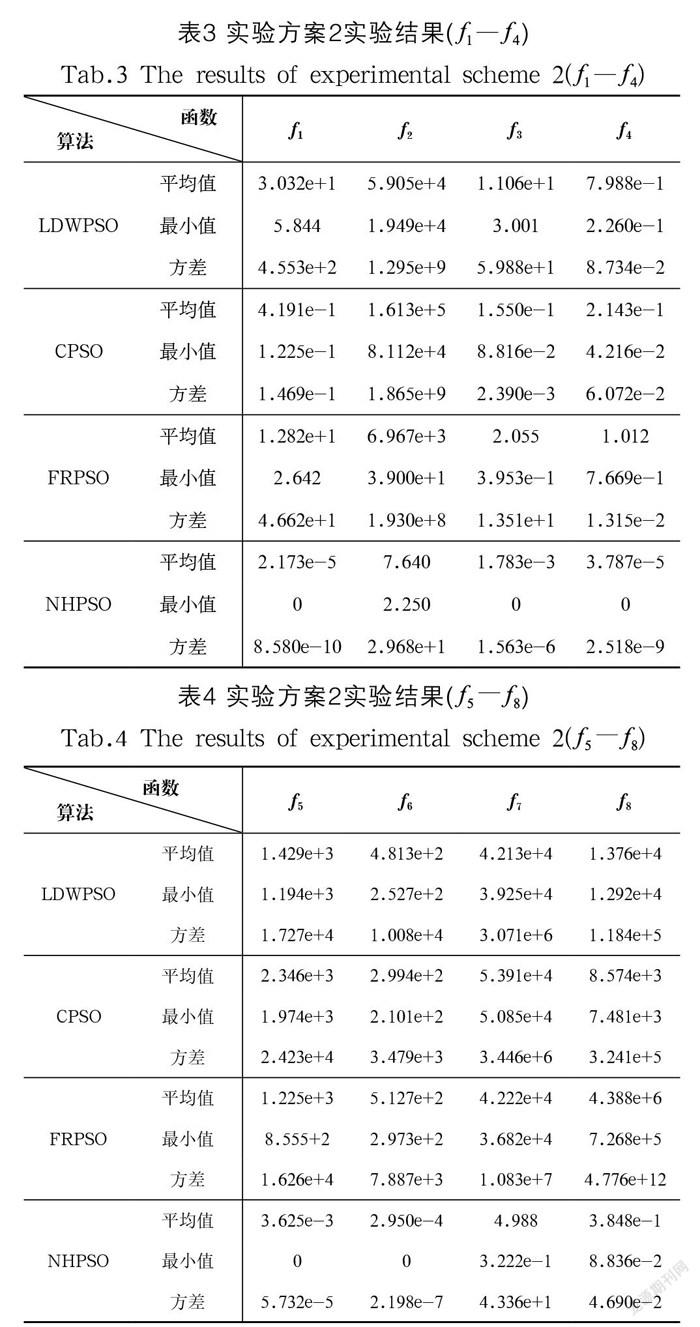
实验方案2：固定，比较算法在时的平均值、最小值、方差。此方案中，。实验结果如表3和表4所示，从至在时的进化曲线如图3至图10所示。

4.3   实验结果

表2、表3、表4是八个标准测试函数在实验方案1和方案2下得到的实验结果。

图3至图10分别是八个测试函数分别在LDWPSO、FRPSO、CPSO和NHPSO下的迭代进化图。

由上述实验结果可以看出，NHPSO无论在收敛精度、收敛速度还是收敛率方面，都要显著优于其他三种算法，并且在后期仍有很强的全局搜索能力，有效抑制了粒子早熟。这主要得益于NHPSO有较为适中的惯性权重，使之能在进化初期搜索到一个较好的候选优化位置，在进化后期收斂的同时仍具有较强的全局搜索能力;在每一次迭代中，对满足条件的粒子采取了一种新的自适应变异策略，提高了种群的多样性。

5   结论（Conclusion）

本文针对PSO算法的早熟收敛问题，提出了一种新的混合粒子群优化算法——NHPSO算法。在NHPSO中，使用新惯性权重策略有效平衡了粒子的全局搜索能力和局部搜索能力;在每次迭代中，按确定条件选择（而不是随机选择）粒子并对其进行新的自适应变异，不仅有利于算法的稳定性，而且有效抑制了粒子早熟。数值仿真实验证实了以上两点。

由于NHPSO在100 维和200 维有很好的优化效果，因此是一种很有实用价值的智能优化算法。

参考文献（References）

[1] SHI Y， EBERHART R. A modified particle swarm optimizer[C]// IEEE.1998 Proceedings of the IEEE International Conference on Evolutionary Computation（CEC）. Piscataway， USA： IEEE， 1998：69-73.

[2] 黄轩，张军，詹志辉.基于随机惯量权重的快速粒子群优化算法[J].计算机工程与设计，2009，30（03）：55-57.

[3] LIANG S J， SONG S L， LI K， et al. An improved particle swarm optimization algorithm and its convergence analysis[C]// IEEE. 2nd International Conference on Computer Modeling and Simulation（ICCMS）. New York， USA： IEEE， 2010：

138-141.

[4] 杨英杰.粒子群算法及其应用研究[M].北京：北京理工大学出版社，2017：1-186.

[5] 李根.基于云任务调度及粒子群算法的网络安全系统设计[J].软件工程，2018，21（05）：28-30.

[6] 赵红超，周洪庆，王书湖.无人机三维航迹规划的量子粒子群优化算法[J].航天控制，2021，39（01）：40-45.

[7] 陈强，王宇嘉，梁海娜，等.目标空间映射策略的高维多目标粒子群优化算法[J].智能系统学报，2021，16（02）：362-370.

[8] 田梦丹，梁晓磊，符修文，等.具有博弈概率选择的多子群粒子群算法[J].计算机科学，2021，48（10）：67-76.

[9] 杨博雯，钱伟懿.多惯性权重的自适应粒子群优化算法[J].渤海大学学报，2021，42（01）：45-52.

[10] 王建丽.基于随机微粒群算法的开放实验室规划研究[J].软件工程，2021，24（10）：28-30.

作者简介：

徐生兵（1980-），男，硕士，讲师.研究领域：智能计算及其应用.

蹇   柯（1983-），男，硕士，讲师.研究领域：智能优化，盲源分离.

夏文杰（1981-），男，硕士，讲师.研究领域：计算机专色油墨配色的理论与实现.