基于扩展卡尔曼滤波的球形机器人姿态解算

龙子洋 项鹏 隋国荣

摘  要：针对球形机器人在姿态解算的过程中，惯性测量元件精度不高、稳定性差和易受噪声干扰从而导致无法精确控制其运动姿态的问题，提出一种通过扩展卡尔曼滤波融合IMU（Inertial Measurement Unit）惯性测量元件数据来进行姿态解算的方法，利用多传感器测量数据进行融合，并使用扩展卡尔曼滤波得到精确的姿态信息。通过相关实验充分验证了基于扩展卡尔曼滤波的姿态解算方法的精度和鲁棒性明显提高，抗噪声干扰能力更强。实验表明，该姿态解算方法相比于互补滤波的姿态解算，全姿态角均方根误差和平均误差分别下降了0.0601和0.1984，可见其对于球形机器人的运动控制具有良好的适用性。

关键词：球形机器人;扩展卡尔曼滤波;互补滤波;姿态解算;四元数

中图分类号：TP273     文献标识码：A

Attitude Calculation of Spherical Robot based on Extended Kalman Filter

LONG Ziyang， XIANG Peng， SUI Guorong

（College of Opto-electronic Information and Computer Engineering， University of Shanghai for Science and Technology， Shanghai 200093， China）

lzy_1194633164@163.com; charlottexp@163.com; suigr@usst.edu.cn

Abstract： In the process of attitude calculation of spherical robot， the inertial measurement element has problems of low accuracy， poor stability and being easy to be disturbed by noise， which makes it impossible to accurately control its motion attitude. In view of these problems， this paper proposes an attitude calculation method which integrates extended Kalman filter and IMU （Inertial Measurement Unit） data. Multi-sensor measurement data is used for fusion and extended Kalman filter is used to obtain accurate attitude information. Relevant experiments fully verifies that the accuracy and robustness of the attitude calculation method based on extended Kalman filter are significantly improved， and the anti-noise interference ability is stronger. Experiments show that compared with the attitude calculation of complementary filter， the root mean square error and average error of the full attitude angle have decreased by 0.0601 and 0.1984 respectively. It can be seen that this method has good applicability for the motion control of spherical robot.

Keywords： spherical robot; extended Kalman filter; complementary filter; attitude calculation; quaternion

1   引言（Introduction）

球形機器人作为一种新型移动机器人，其所有机械结构和控制系统都包含于球形外壳内，通过质心偏移、动量守恒等[1]原理实现球形机器人的全向移动，其具有运动能力强、抗倾倒和能耗低等特点。因此，球形机器人在安防巡检、危险环境探测和野外侦察等[2]领域具有十分广阔的应用前景。

球形机器人具有独特的机械结构和运动方式，由于其运动姿态具有明显的非线性特征，实时获取球形机器人的姿态信息对其运动控制至关重要。近年来，IMU多传感器融合广泛应用于导航系统和姿态解算。但是，球形机器人工作时因惯性元件受随机噪声和外力加速度等因素的干扰，导致获取的姿态角误差增大和控制稳定性下降等问题。2013 年，李景辉等[3]通过PI（Proportion Integration）调节和互补滤波进行控制，提高了角速度精度;2016 年，ALLOTTA等[4]提出无迹卡尔曼滤波，减小了系统的线性误差，但是计算量相对较大;2021 年，余晨雨等[5]提出的基于互补滤波和粒子滤波融合的球形机器人姿态解算方法，提高了球形机器人姿态解算的实时性和准确性。

针对IMU惯性测量元件精度不高、稳定性较差和易受随机噪声干扰等问题，本文通过扩展卡尔曼滤波融合IMU的测量数据来进行姿态解算。考虑四元数偏差和角速度的误差，结合加速度计和磁力计的测量值，利用扩展卡尔曼滤波更新四元数以得到实时的全姿态角，并设计实验对所提出的姿态解算系统进行验证。

2   球形机器人系统设计（System design of spherical robot）

本文所搭建的球形机器人系统如图1所示，由圆形透明外壳球和内部硬件驱动模块组成，通过控制舵机改变万向轮，驱动电机来实现运动及转向等功能。透明球壳由两个直径25 cm的圆形透明亚克力半球拼装组合而成;内部驱动硬件模块包括含有两个霍尔编码器（额定功率为4.32 W）的直流电机，四节功率为5500 mWh的18650锂电池，一个电源分配板向核心板和电机供电，24 块铝块配重块（每块5 g）降低机器人重心。

图2为系统的控制结构。本文球形机器人系统采用STM32F103C8T6作为核心板;对于IMU模塊，采用MPU6050整合的六轴传感器获取陀螺仪和加速度计的数据，采用MAG3110三轴磁力计获取磁场强度信息;使用HC05蓝牙作为无线通信模块，根据自定义通信协议将姿态数据发送至上位机。

3   姿态解算与滤波算法（Attitude calculation and filtering algorithms）

3.1   欧拉角与四元数姿态解算

球形机器人的姿态角获取通常是将陀螺仪、加速度计和磁力计的测量值进行数据融合的滤波姿态解算，在计算过程中涉及两个坐标系之间的变换。其中惯性导航坐标系对应的为北东地（North East Down，NED）坐标系，而通常惯性传感元件的测量值定义在载体坐标系B中。通过惯性导航坐标系与载体坐标系不同X、Y、Z轴对应的夹角来描述载体的欧拉角，、和分别为俯仰角（pitch）、横滚角（roll）和偏航角（yaw），如图3所示。

用、、和、、分别表示惯性导航坐标系和载体坐标系，两者空间关系对应如下：

（1）

式（1）中，为惯性导航坐标系到载体坐标系的变化矩阵。设四元数[6]，通过四元数表示为：

（2）

由式（2）中的四元数转移矩阵可以得到四元数和欧拉角的转换关系为：

（3）

四元数的微分方程，写成矩阵形式为：

（4）

式（4）中，为利用传感器进行数据融合得到的载体坐标系下的三轴角速度。

球形机器人在探测、执行任务的过程中对姿态解算的精度与实时性具有较高的要求，通过多传感器进行数据融合得到三轴角速度信息，接着利用一阶龙格库塔法进一步更新四元数可以得到：

（5）

再结合式（3）可以得到实时更新的欧拉角[7]。

3.2   基于互补滤波的姿态估计

互补滤波算法通过不同传感器噪声的特性来实现姿态解算。陀螺仪具有良好的动态响应特性，其在较短的时间内具有很高的解算精度。然而随着时间的增加，积分的误差会逐渐增大，加速度计和磁力计解算的姿态角在短时间内精度较差，但测量误差不随着时间累积。因此，将陀螺仪获得的瞬时姿态角和加速度计、磁力计长时间积分计算得到的姿态角分别作为互补滤波器的两个输入。互补滤波器利用两者在频域上的互补特性提高姿态角的解算精度。对大多数互补滤波使用PI调节[8]，即：

（6）

其中，为比例调节，能够及时成比例地反映系统的偏差，比例增益的大小决定了滤波器的截止频率;为积分调节，能够使系统消除稳态误差，适当地减小积分增益能够提升滤波的性能。基于PI调节的互补姿态解算流程图如图4所示，其中Minimum error为根据实际情况设置的最小误差值。

分别将导航坐标系下的重力加速度和地磁场通过矩阵转移到载体坐标系下，并且进行归一化后得到加速度计测量值和磁力计测量值。接着，对转化前后的矢量进行叉乘得到矢量之间的误差角，总误差矢量为：

（7）

通过PI调节和矢量误差对陀螺仪得到的角速度进行修正可得：

（8）

式（8）中，为t时刻的角速度，为更新的角速度，利用修正后的角速度更新四元数进而反解得到欧拉角。

3.3   基于扩展卡尔曼滤波的姿态估计

卡尔曼滤波[9]是一种线性最小方差估计，其通过方差对测量值和预测值进行加权而得到系统的估计值，广泛使用于实时系统和嵌入式系统。其基本式如下：

（9）

式（9）中，为第k时刻的一步状态估计，表示上一时刻的状态估计值;为状态矩阵，为一步预测均方误差阵，为系统噪声矩阵;为测量矩阵，表示测量值和状态量之间的关系，为测量噪声矩阵;表示第k时刻的状态估计，表示第k时刻的测量值;表示第k时刻的估计均方误差矩阵，为单位矩阵。其中，前两项式表示状态更新，后三项式表示测量更新。通过给定初值和，利用第k时刻的测量值递推计算得到第k时刻的状态估计值。

上述经典的卡尔曼滤波更适用于已知噪声的先验统计的线性控制系统，但球形机器人属于非线性系统，测量噪声和系统噪声较难获取，不确定性高，实时性差，并且姿态解算抗干扰的能力较弱，因此采用基于扩展卡尔曼滤波的姿态解算来对球形机器人进行姿态估计。

在扩展卡尔曼滤波算法中，通过将陀螺仪的偏差和四元数的误差作为状态量，分别将磁力计和加速度计的测量值作为对应的测量更新，进而利用角速度误差纠正四元数，最终求得全姿态角。基于扩展卡尔曼滤波姿态解算原理的设计如图5所示。

4   实验与分析（Experiments and analysis）

为了验证本文所提出的姿态解算算法的精度与有效性，本文对以STM32F103C8T6为核心板搭载的球形机器人进行实验。系统利用Keil软件进行编程，通过MPU6050获得的陀螺仪和加速度计数据，以及磁力计MAG3110得到的磁场强度分别进行基于互补滤波算法和扩展卡尔曼滤波算法的姿态解算，获得不同解算得到的全姿态角数据。利用蓝牙串口通信导出数据并通过Python软件进行作图对比，从不同波形比较俯仰角、横滚角和偏航角的解算结果。

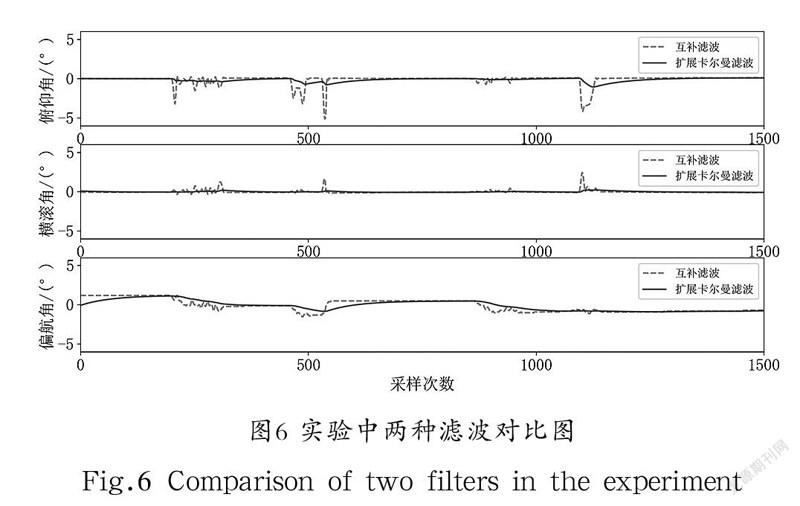
实验具体步骤为首先保持球形机器人三轴固定，设置采样频率为10 Hz，选取连续采样150 s的数据，得到不同算法下的俯仰角、横滚角和偏航角，将对比结果绘制成波形，如图6所示。

从图6可以看出，相对于互补滤波，基于扩展卡尔曼滤波的姿态解算能够有效抑制高频噪声，减小姿态角数据突变率，并且使得姿态角曲线变得平滑，提高了控制精度和鲁棒性。

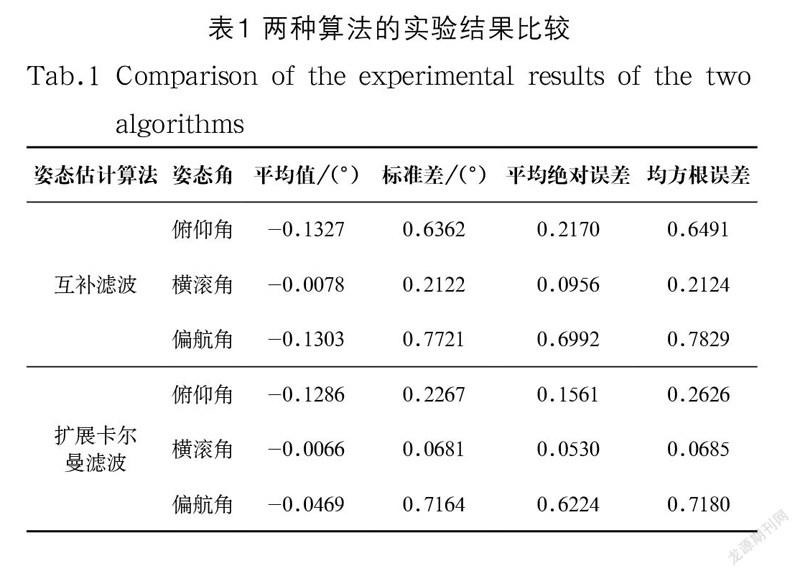
在实验中，理想的俯仰角、横滚角和偏航角输出都应该为0°，引入四种误差性能指标进行综合评价。从表1中互补滤波与扩展卡尔曼滤波对比结果可得出，后者四个误差比较指标都有所下降。以横滚角为例，扩展卡尔曼滤波算法相比于互补滤波的姿态解算，其均方根误差下降0.1439，平均绝对误差下降0.0426。对于全姿态角，经表1数据计算，其均方根误差和平均绝对误差分别下降了0.0601和0.1984。从实验中可以看出，扩展卡尔曼滤波算法在球形机器人系统下的姿态解算比互补滤波算法更为精确，波动范围更小，抗噪声干扰能力更强，总体曲线更加趋近于理论结果。

5   结论（Conclusion）

本文针对基于IMU多传感器的惯性测量元件精度不高、稳定性较差和易受随机噪声干扰等问题，提出一种基于扩展卡尔曼滤波的球形机器人姿态解算方法，利用该算法实时更新四元数以反解欧拉角获取全姿态信息。本文基于搭建的球形机器人系统，设计实验比较本文算法和互补算法的姿态解算结果，相比之下，扩展卡尔曼滤波算法的姿态精度更高，抗噪声干扰和收敛性效果更加显著。因此，本文提出的姿态解算方法在球形机器人的运动控制等领域具有良好的适用性，未来还需在球形机器人控制领域做进一步研究，以期得到更优的姿态解算效果。

参考文献（References）

[1] LI M， GUO S， HIRATA H， et al. Design and performance evaluation of an amphibious spherical robot[J]. Robotics and Autonomous Systems， 2015（64）：21-34.

[2] 戰强，李伟.球形移动机器人的研究进展与发展趋势[J].机械工程学报，2019，55（09）：1-17.

[3] 李景辉，杨立才.基于多传感器信息融合的人体姿态解算算法[J].山东大学学报（工学版），2013，43（05）：49-54.

[4] ALLOTTA B， CAITI A， CHISCI L， et al. An unscented Kalman filter based navigation algorithm for autonomous underwater vehicles[J]. Mechatronics， 2016（39）：185-195.

[5] 余晨雨，章政，黄卫华，等.基于互补滤波和粒子滤波融合的球形机器人姿态解算[J].机器人，2021，43（03）：340-349.

[6] 贾瑞才.基于四元数EKF的低成本MEMS姿态估计算法[J].传感技术学报，2014，27（01）：90-95.

[7] 秦永元.惯性导航[M].北京：科学出版社，2006：298-300.

[8] 张泽权.基于MEMS的运动捕捉装置及姿态解算算法设计[D].杭州：浙江大学，2021.

[9] 张栋，焦嵩鸣，刘延泉.互补滤波和卡尔曼滤波的融合姿态解算方法[J].传感器与微系统，2017，36（03）：62-65，69.

作者简介：

龙子洋（2000-），男，本科生.研究领域：多传感器融合导航控制.

项   鹏（2000-），男，本科生.研究领域：多传感器融合导航控制.

隋国荣（1974-），男，博士，副教授.研究领域：光电检测，机器视觉.本文通信作者.