基于行波理论的输电线路故障诊断方法研究

李立江 林海 王佳 陈换过 胡旭晓

摘  要：运行中的输电线路发生故障时，会在故障点产生向两侧传播的电流行波和电压行波。电流行波和电压行波又统称为故障行波，故障行波会在阻抗不连续点发生折射和反射，由此可以通过采集并分析故障行波得到线路故障信息。利用相模变换对三相电流行波进行解耦，通过解耦后得到的独立模量之间的关系可以确定故障类型和故障相，再利用小波变换模极大值的方法标定行波波头，通过波头信息可以得到故障点距离。仿真结果显示，该方法能准确地确定故障类型和故障相，对故障点距离的定位也能达到很高的精度。

关键词：输电线路;行波;故障诊断;小波变换;MATLAB

中图分类号：TP206.3     文献标识码：A

Research on Fault Diagnosis Method of Transmission Line

based on Traveling Wave Theory

LI Lijiang1， LIN Hai2， WANG Jia2， CHEN Huanguo2， HU Xuxiao2

（1.Beijing Sihuida Power Technology Co.， Ltd.， Beijing 101520， China;

2.School of Mechanical Engineering and Automation， Zhejiang Sci-Tech University， Hangzhou 310018， China）

26027960@qq.com; 2049535531@qq.com;Wangjiajia1118@163.com;

chen8025@126.com; huxuxiao@zju.edu.cn

Abstract： When a fault occurs in a running transmission line， a current traveling wave and a voltage traveling wave that propagate to both sides will be generated at the fault point. The current traveling wave and the voltage traveling wave are also collectively referred to as fault traveling waves， which will refract and reflect at the impedance discontinuity point. Therefore， line fault information can be obtained by collecting and analyzing fault traveling waves. The three-phase current traveling wave is decoupled by phase-mode transformation， and fault type and fault phase can be determined through the relationship between the independent moduli obtained after decoupling. Then the traveling wave head is calibrated by the method of wavelet transform modulus maxima， and the fault point distance can be obtained by the wave head information. The simulation results show that the method can accurately determine the fault type and fault phase， and it can also achieve high accuracy in locating the fault point distance.

Keywords： transmission line; traveling wave; fault diagnosis; wavelet transform; MATLAB （Matrix Laboratory）

1   引言（Introduction）

輸电线路是电力系统的重要组成部分，其输送距离长，跨越距离广，沿途气候及环境多变，所以发生故障的概率高，而故障处理的及时性将决定经济损失的大小，故障定位的精确度有助于输电线路故障的抢修。目前使用在输电线路中的故障定位方法主要有阻抗法和行波法两种。阻抗法的原理是根据故障时测得的电压和电流计算出故障回路的阻抗，由于线路长度与阻抗成正比，由此可以求出故障点位置，但阻抗法易受过度电阻、线路分布电容、线路模型和运行方式等多变因素影响，所以测量精度不高[1]。输电线路实际应用更多的是行波法，它是利用故障点产生的暂态行波分析得到故障相关信息，从原理上讲，其测量精度与线路长度、结构、过度电阻无关，能达到高精度故障诊断[2]。本文通过分析故障行波及其在输电线路上的传播特性，利用MATLAB建立仿真模型，对基于行波理论的故障诊断方法进行深入研究。

2   行波测距原理（Traveling wave ranging principle）

2.1   行波理论

输电线路发生故障后，会在故障点产生电压和电流的瞬间突变，形成电压和电流暂态分量，并且以接近光速向输电线路的两侧传播，这种暂态分量就称为暂态行波。下面以单根导线为例建立等效电路的数学模型，将电压源接通到输电线路上，以线路微元的角度分析电路，靠近电压源的线路分步电容立即充电，并且经过线路分布电感向相邻的分布电容充电。线路上远处的电容要经过一段时间才充上一定量的电荷，并且向更远的电容放电。电容依次充电，线路沿线就逐渐建立电场并形成电压，即存在电压行波以一定的速度沿线路方向传播[3]。在线路电容的充放电过程中，随着电流流过电感，在导线周围空间建立起磁场，因此也有电流行波以同样的速度沿导线方向传播[3]。在导线中取一微分长度为的导线段，整个均匀传输的导线可视为由无限多个这样的微分段连接而成，其等效电路模型如图1所示。

在一定的时间段内，沿轴正向电压增加量为，电流增加量为。对回路ABCD应用基尔霍夫电压定律，同时对B点应用基尔霍夫电流定律[3]，分别可得到如式（1）和式（2）所示的等式：

（1）

（2）

将式（1）和式（2）两边同除以并取，得到的关系式如式（3）所示：

（3）

对于无损线路，，，式（3）可以简化为式（4）：

（4）

式（4）为理想状态下无损单导线的波动方程。分别对x和t进行微分，就可以得到二阶波动方程，如式（5）所示：

（5）

式（5）的达郎贝尔（D'Alembert）解为：

（6）

式（6）中，为沿输电线路正方向传播的电压行波，为沿输电线路反方向传播的电压反向行波，为沿输电线路正方向传播的电流行波，为沿输电线路反方向传播的电流反向行波。v为行波的传播速度，其计算式[3]为：

（7）

其中，为线路单位长度电感，为线路单位长度电容。

2.2   行波解耦与相模变换

上述理论是以单根导线为基础进行阐述的，而在实际电力系统中都是三相电路，其中一相发生故障时，由于导线上存在电感，三相之间存在电磁耦合，因此非故障相上也会产生行波，且波动方程各相之间是互不独立的[4]。经过长期的探索，诞生了模式传输理论。模式传输理论也被称为模分量分析法或相模变换技术。根据模式传输理论，任意数量平行于地面的传输导线中，每种模式的电压和电流在导线中传播具有相同的传播常数[5]。运用矩阵相似变换，可以把存在耦合的相量变换为相互独立的模量。

存在电磁耦合的三相波动方程如式（8）和式（9）所示：

（8）

（9）

其中，表示单相输电线路单位长度的自感，表示两相输电线路单位长度之间的互感，表示单相输电线路单位长度的对地电容，表示两相输电线路单位长度之间的电容。

由于式（8）和式（9）中的矩阵和矩阵中非对角元素不为零，方程很难求解，为了解决求解问题，可以利用相模变换将相量变换为独立的模量。相模变换中模值与相值之间的关系如下：

（10）

（11）

其中，，，，，为相模变换矩阵。

常用的变换有对称分量变换、Clarke变换、Karenbauer变换，由于Karenbauer变换矩阵结构简单对称，无须复数计算，因此这里选择Karenbauer变换，其相模变换矩阵为：

相模变换过后，a相、b相、c相三相分量变换为线模分量分量、分量和零模分量。线模分量以导线为回路，其中分量在a相导体和b相导体之间流动，分量在a相导体和c相导体之间流动。线模分量波速接近光速，波阻抗比零模分量的波阻抗小，在传播过程中波速不易受到外界因素的影响。零模分量以大地为回路，其阻抗受到土壤的电阻率影响，所以阻抗较大，波速较小[5]。经过解耦后的模分量，其波動方程是完全独立的，可以利用前面单相线路的波动方程，单独求解到各模电流和模电压的值，最后通过相模反变换求得各相电流和相电压。通过对所有模量结合起来分析，可以得到所有的接地故障和短路故障类型。

2.3   单双端行波测距法

当线路发生故障时，根据叠加原理将故障行波等效为故障前正常行波和故障附加行波的叠加，从而可以利用故障附加行波对故障分量单独进行分析。由于短路点故障附加电势的作用，线路在故障点会产生行波，并且沿故障线路传播并经线路母线向整个电网传播，在波阻抗不连续点处发生折射和反射[6]。行波测距就是根据测量多次行波到达行波观测点的时差来计算故障距离。

行波测距方法主要有两大类：双端行波测距法和单端行波测距法，其中A型和D型行波测距原理由于无附加脉冲信号发生装置[7]，因此应用更广泛。A型行波测距原理是根据故障最先到达观测点的初始行波及其后续在故障点的首次反射波到达时间差来计算故障位置，属于单端行波测距法。D型行波测距原理是根据初始行波到达故障线路两端测量点的时间差来计算故障位置，属于双端行波测距法。

如图2所示，以沿x轴反方向传播的行波为例描述A型单端行波测距法。

假设线路在点F处发生接地故障，产生的故障行波沿M端和N端传播，在x轴的反方向，行波到达母线M端的时间为，

在母线M端发生反射后又经故障点F反射回到母线M端的时间为。假设行波的波速为，可以得到故障点F距离母线M端的距离为：

（12）

对于D型双端行波测距法，故障点F产生向母线M端和母线N端的故障行波，到达母线M端的时间为，到达母线N端的时间为。假设行波的波速为，MN的距离为，可以得到故障点F到母线M端的距离为：

（13）

2.4   小波变换理论

由行波测距公式（12）和公式（13）可以看出，无论是单端法还是双端法，行波波头的识别准确性十分重要。与初始行波相比，后续行波的衰减十分严重，并且难以同干扰波分开，单端测距所需要的第二个波特的检测十分困难。近年来由于小波理论的迅速发展，如今已成为行波波头分析最有效的方法之一[8]。小波变换有着严密、坚实的数学基础，其特有的多分辨率分析思想和良好的时频局部变换奇异分析功能，对行波波头检测表现出十分良好的效果。函数的小波变换可定义为：

（14）

式（14）中，a为伸缩因子，b为位移因子，a和b连续变换成为连续小波函数。通过小波变换对故障行波进行分解，小波变换的模极大值与奇异点是一一对应的，可以将模极大值出现的点作为行波到达的时刻[9]。

3  故障类型及故障相判定（Fault type and fault phase judgment）

由于采集到的行波信号是故障前正常行波与故障附加行波的叠加，因此将采集到的行波信号减去线路正常运行时的行波信号，就可以得到故障附加行波信号，再对所得到的故障附加行波信号进行相模变换，可得到故障附加行波的模值。下面对电流行波信号进行分析。

假设采集到的电流行波信号为、、，线路正常运行时的电流行波信号为、、，可以得到故障附加电流行波信号为：

（15）

利用式（2）—式（11）的Karenbauer变换对故障附加电流和行波信号进行相模变换，可以得到零模分量取模后的值和线模分量取模后的值、，最后结果如下：

（16）

为了便于进行模量分析，引入一个线模分量，由于其与、构成三相回路，其中分量在a相导体和b相导体之间流动，分量在a相导体和c相导体之间流动，因此应该在b相导体和c相导体之间流动，其值应为：

（17）

利用不同模量之间的关系，可以得到不同的故障类型，具体可分为单相接地、两相接地、三相短路但不接地和两相短路但不接地。根据零模分量的性质，发生接地故障时零模分量不为零，发生相间短路故障时零模分量为零。

如果=0，线路发生短路但不接地故障，故障相判别方式如下：

当时，a、b、c三相间发生短路但不接地故障;

当时，a、b两相间发生短路但不接地故障;

当时，b、c两相间发生短路但不接地故障;

当时，a、c两相间发生短路但不接地故障。

如果，线路发生接地故障，故障相判别方式如下：

当时，a相发生接地故障;

当时，b相发生接地故障;

当时，c相发生接地故障;

当时，a、b两相发生接地故障;

当时，a、c两相发生接地故障;

当时，b、c两相发生接地故障。

4  MATLAB仿真分析（MATLAB simulation analysis）

4.1   故障类型和故障相仿真分析

MATLAB软件是一个功能强大的科学计算软件，不但具有强大的数值计算功能，而且还提供许多扩展功能模块，包括本文用到的电力系统模块库（Power System Blockset）和小波分析工具箱（Wavelet Toolbox）。MATLAB还具有良好的图形绘制功能，使得到的仿真结果易于分析和理解。本文仿真流程如图3所示。

利用MATLAB/SIMULINK软件建立如图4所示的输电线路仿真模型。

三相电源的电源kV，相位角为0°，频率为50 Hz，电源的阻抗 Ω，电源电感 H，线路L1长度为90 km，线路L2长度为110 km。

线路正序电感mH/km，正序阻抗 Ω/km，正序电容 nF/km。

线路零序电感mH/km，零序阻抗 Ω/km，零序电容 nF/km。

正常運行时的三相电流波形如图5所示，图中深色实线代表a相，虚线代表b相，浅色点线代表c相。

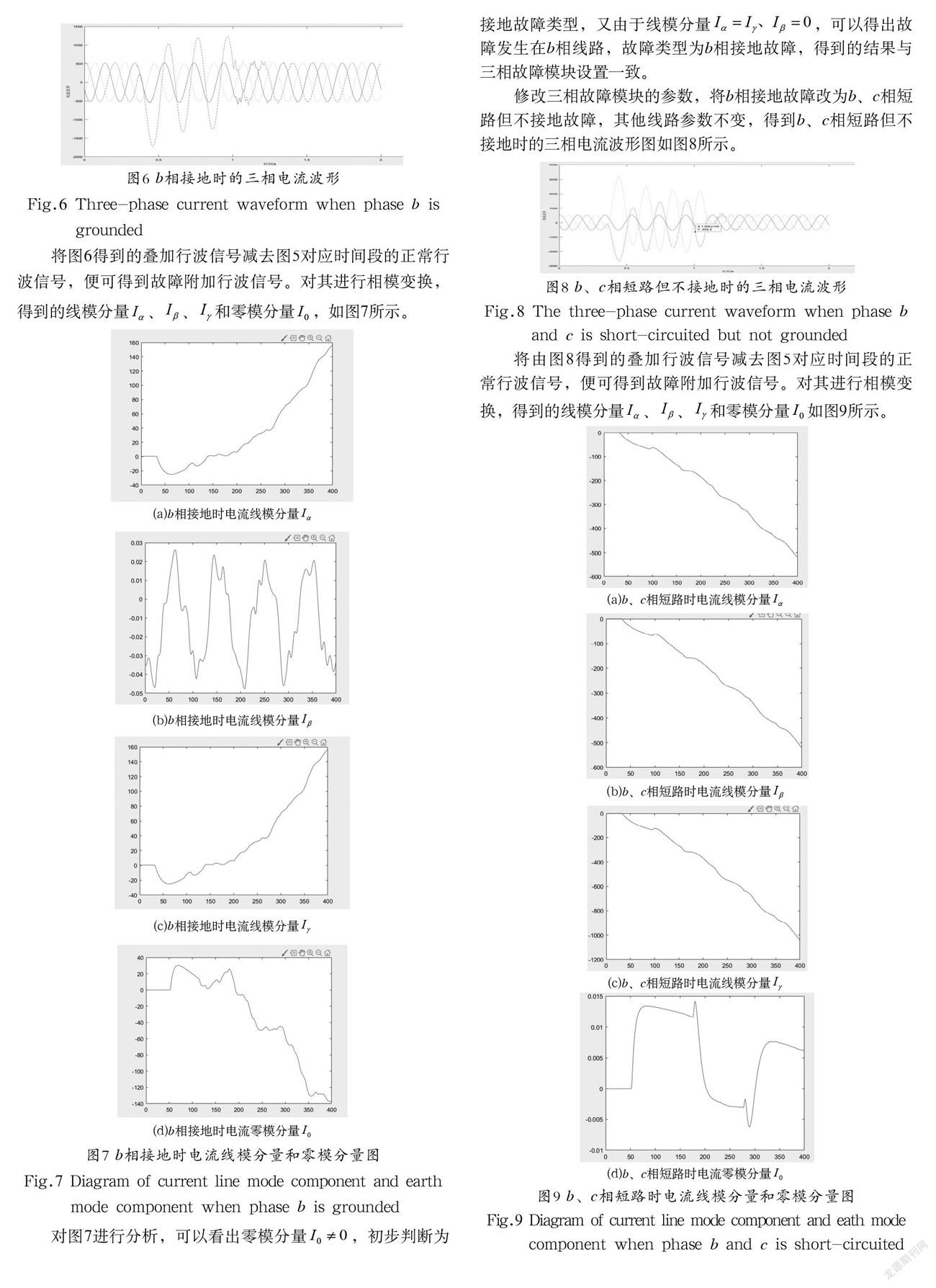
利用三相线路的故障模块模量b相接地故障，设置采用频率为1 MHz，仿真总时长为0.2 s，设置故障发生时间为0.035—0.1 s。通过仿真得到波形图如图6所示。

将图6得到的叠加行波信号减去图5对应时间段的正常行波信号，便可得到故障附加行波信号。对其进行相模变换，得到的线模分量、、和零模分量，如图7所示。

对图7进行分析，可以看出零模分量，初步判断为接地故障类型，又由于线模分量，可以得出故障发生在b相线路，故障类型为b相接地故障，得到的结果与三相故障模块设置一致。

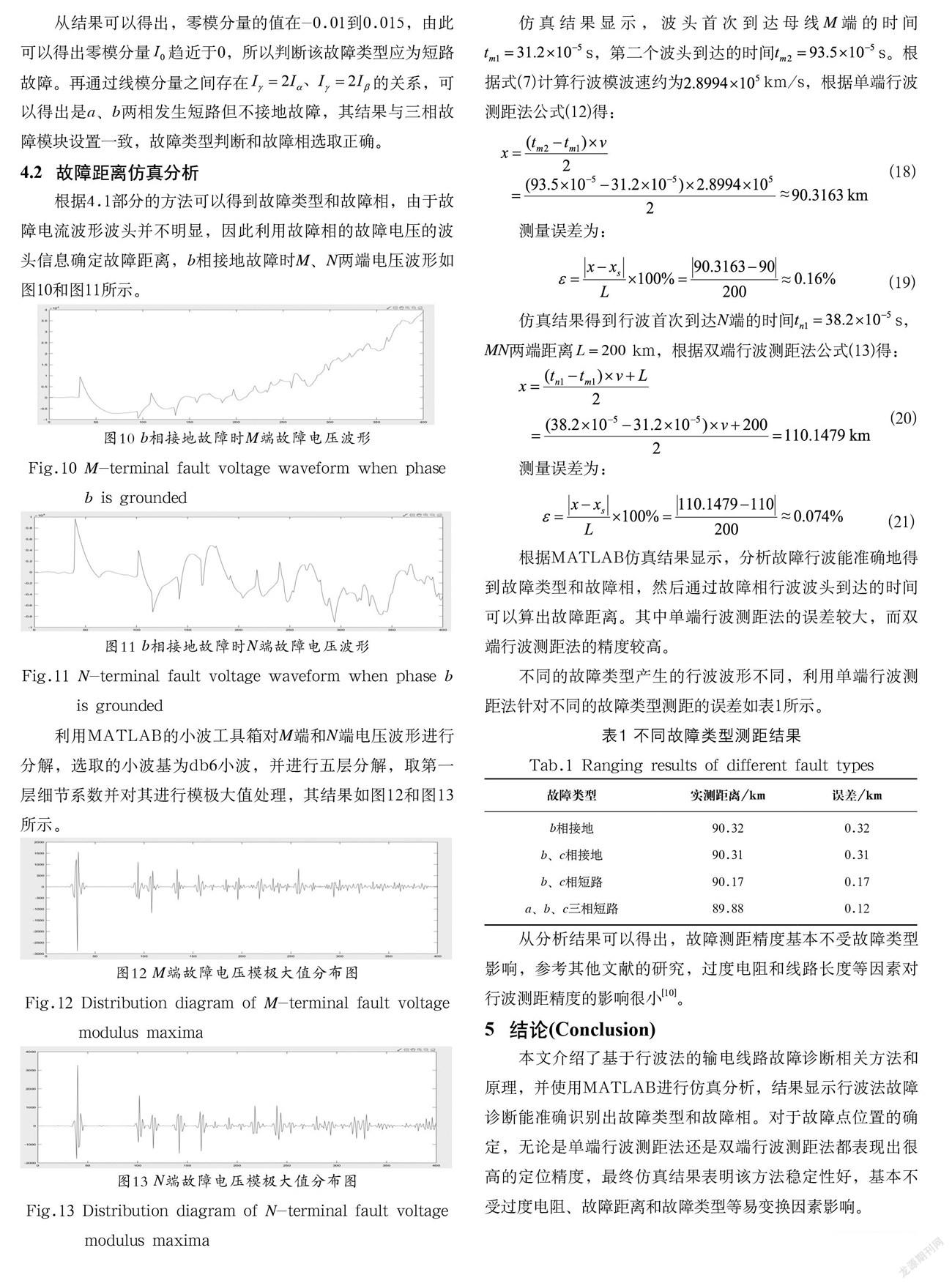
修改三相故障模块的参数，将b相接地故障改为b、c相短路但不接地故障，其他线路参数不变，得到b、c相短路但不接地时的三相电流波形图如图8所示。

将由图8得到的叠加行波信号减去图5对应时间段的正常行波信号，便可得到故障附加行波信号。对其进行相模变换，得到的线模分量、、和零模分量如图9所示。

从结果可以得出，零模分量的值在-0.01到0.015，由此可以得出零模分量趋近于0，所以判断该故障类型应为短路故障。再通过线模分量之间存在的关系，可以得出是a、b两相发生短路但不接地故障，其结果与三相故障模块设置一致，故障类型判断和故障相选取正确。

4.2   故障距离仿真分析

根据4.1部分的方法可以得到故障类型和故障相，由于故障电流波形波头并不明显，因此利用故障相的故障电压的波头信息确定故障距离，b相接地故障时M、N两端电压波形如图10和图11所示。

利用MATLAB的小波工具箱对M端和N端电压波形进行分解，选取的小波基为db6小波，并进行五层分解，取第一层细节系数并对其进行模极大值处理，其结果如图12和图13所示。

仿真结果显示，波头首次到达母线M端的时间 s，第二个波头到达的时间 s。根据式（7）计算行波模波速约为 km/s，根据单端行波测距法公式（12）得：

（18）

测量误差为：

（19）

仿真结果得到行波首次到达N端的时间 s，MN两端距离 km，根据双端行波测距法公式（13）得：

（20）

测量误差为：

（21）

根据MATLAB仿真结果显示，分析故障行波能准确地得到故障类型和故障相，然后通过故障相行波波头到达的时间可以算出故障距离。其中单端行波测距法的误差较大，而双端行波测距法的精度较高。

不同的故障类型产生的行波波形不同，利用单端行波测距法针对不同的故障类型测距的误差如表1所示。

从分析结果可以得出，故障测距精度基本不受故障类型影响，参考其他文献的研究，过度电阻和线路长度等因素对行波测距精度的影响很小[10]。

5   结论（Conclusion）

本文介绍了基于行波法的输电线路故障诊断相关方法和原理，并使用MATLAB进行仿真分析，结果显示行波法故障诊断能准确识别出故障类型和故障相。对于故障点位置的确定，无论是单端行波测距法还是双端行波测距法都表现出很高的定位精度，最终仿真结果表明该方法稳定性好，基本不受过度电阻、故障距离和故障类型等易变换因素影响。

参考文献（References）

[1] 苏丽娜.高压输电线路接地故障定位技术的研究[D].长春：长春工业大学，2012.

[2] 刘振亚.基于行波的输电线路故障测距方法研究[D].徐州：中国矿业大学，2019.

[3] 束洪春.行波暂态量分析与故障测距[M].北京：科学出版社，2016：18-69.

[4] EVRENOSOGLU C Y， ABUR A. Travelling wave based fault location for teed circuits[J]. IEEE Transactions on Power Delivery， 2005， 20（2）：1115-1121.

[5] 田梦楚.基于行波理论的110kv线路距离保护研究[D].南京：南京理工大学，2012.

[6] 傅国庆.暂态行波信息融合的输电线路故障定位方法研究[D].徐州：中国矿业大学，2016.

[7] 覃剑，葛维春，邱金辉，等.输电线路单端行波测距法和双端行波测距法的对比[J].电力系统自动化，2006（06）：92-95.

[8] 汪敏.小波变换在输电线路行波故障测距中的应用[D].北京：华北电力大学，2014.

[9] 爱玉，卢正通，贾文官.基于小波模极大值理论的架空输电线路故障测距研究[J].电工电气，2018（10）：49-53.

[10] 徐高，瞿峰，周强.基于小波分析法的行波故障测距方法研究[J].电工电气，2021（02）：49-52，73.

作者简介：

李立江（1977-），男，本科，中级工程师.研究领域：电网监测.

林   海（1998-），男，硕士生.研究领域：输电线路故障诊断.

王   佳（1998-），女，碩士生.研究领域：六自由度机械臂轨迹跟踪控制.

陈换过（1977-），女，博士，教授.研究领域：故障预测，机械零部件可靠性.

胡旭晓（1965-），男，博士，教授.研究领域：图像处理，机器人轨迹跟踪控制.