滑坡趋势的EMD-ANN方法预测

倪晓兰

（兰州交通大学数理学院，甘肃兰州 730070）

地质灾害（如地震、火山、滑坡、泥石流等）的频繁发生对人们的生活产生了一定的影响，其中滑坡无疑是一个最具危害性的隐患，每年都会对人们的生命财产安全造成大量的损害，对国家建设造成不可忽略的影响，因此开展对滑坡破坏问题的研究，了解滑坡的破坏趋势及其影响范围，对避免和减轻滑坡灾害带来的损失具有至关重要的作用，也对做好滑坡防治工作具有非常重要的现实意义.

产生滑坡的原因很多，国内外许多学者对滑坡破坏的研究非常广泛. 有的学者对滑坡位移进行预测，如成枢[1]等引入非线性惯性权重改进粒子群优化BP 网络模型，提出IPSO-BP 模型，相比于其他模型，该模型与实测数据拟合结果更接近，进而对滑坡位移趋势有较好的预测；刘红帅[2]等以中里滑坡为例利用改进的灰色预测模型—等维灰数递补动态预测模型进行滑坡位移预测；刘先珊[3]等提出基于退火交替迭代算法神经网络的位移预测方法，其预测精度明显优于BP 神经网络. 有的学者主要针对滑坡进行空间预测，如张敬一[4]、陈伟[5]、韩高[6]等分别介绍了滑坡灾害空间预测常用的理论方法以及各类空间滑坡灾害发展趋势，用最先进的人工智能算法组成的混合集成方法进行滑坡空间预测研究，采用Logistic 回归（LR）和支持向量机（SVM）对滑坡进行空间分类；Nguyen[7]等利用朴素贝叶斯对越南白岩省木仓柴区进行滑坡预测模型对比分析；蔡欣育[8]等针对降雨不同对边坡稳定性的影响进行研究，发现边坡失效概率随着降雨强度的增加而增大. 虽然很多学者对滑坡进行了不同角度的分析与研究，针对滑坡位移和滑坡空间预测的研究较多，对滑坡边坡稳定的研究也很广泛，但是对滑坡破坏趋势、滑坡破坏趋势预测等研究相对较少.

20 世纪80 年代以来，人工智能研究成为热点.李春生[9]利用FLAC3D数值模拟手段，对滑坡时空破坏规律进行了研究. 丁守銮[10]等利用动态学习比率BP 算法以双曲正切函数为功能函数的非线性时间序列预测方法，建立HFRS 发病率的ANN 预测模型. 蔡钊[11]等采用ARIMA-ANN 组合能量预测模型对OLSR 路由节点的剩余电量进行预测. Banga[12]等利用多元人工神经网络技术来评估和预测散装存储的豆类密度.潘大丰[13]等利用BP算法提出了时间序列和信息预测方法，并对比证实了该方法比统计回归模型有较强的预测能力. 本文借鉴以上方法，研究降雨和坡角不同时工况，分析滑坡破坏程度的大小，针对滑坡破坏趋势，提出一种基于经验模态分解（EMD）的人工神经网络（ANN）智能预测法（EMD-ANN），将原始序列进行经验模态分解后，进行人工神经网络预测滑坡破坏趋势.

1 经验模态分解

1.1 数据处理

数据来源于室内模拟坡角为30°的后锋降雨滑坡实验采集的三维点云数据（一组在三维坐标系统中组成的向量的集合）.根据三维点云数据画出滑坡滑动曲线，如图1所示.

图1 滑坡断裂曲线

用图像二值化处理，即用OpenCV 中的threshold 函数获取二元值的灰度图像（如图2），该函数中有四个参数：第一个参数表示原图像，第二个是分类的阈值，第三个参数是高于（或低于）阈值赋予的新值，第四个是阈值类型. 最后提取出由二维像素点坐标构成的滑坡滑动曲线.

图2 图像二值化处理

图像二值化处理后将所有曲线放入同一坐标，如图3 所示，接着固定x轴坐标，提取不同时刻的y轴坐标，由于x从小到大排序后中间有缺失值，补全缺失值的同时，y此时不是一一对应，因此取x未缺失的前后数值所对应的y值对其求平均进行插值，进而提取出x所对应的不同时刻的所有y值. 最终提取得到207 个不同的x，每个x对应102 个不同时刻的y值. 选取间隔一样的10 个不同x值所对应的不同时刻的y值进行预测，即X1，...，X10对应的Y1，1-Y1，102，...，Y1，10-Y10，102，对此10组不同的y进行预测.

图3 提取的若干曲线在同一平面展示

1.2 经验模态分解步骤

由于提取到的数据直接做预测误差会很大，因此将数据进行经验模态分解，从而减少误差，提高精度. 经验模态分解的本质是通过特征时间尺度来识别信号中所包含的所有振动模态，即将一组分布不规则的数据转化为多组分布规则的数据和残差项数据的形式.用公式可以表示为：

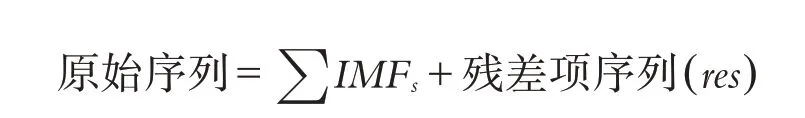
其分解方法有三个假设条件：首先数据至少要有一个最大值和一个最小值以及有两个极值；其次，局部时域特性是由极值点间的时间尺度唯一确定；最后，当数据中无极值点但是有拐点，那么可以通过对数据求导求极值，接着通过积分获得分解结果.

EMD分解步骤如下[14]：

第一步，根据原始序列确定X( )t的极大、极小值点.

第二步，由第一步分别画出原始数据的上、下外包络线；第二部，求出上G(t)、下H(t)外包络线.

第三步，画出均值包络线：

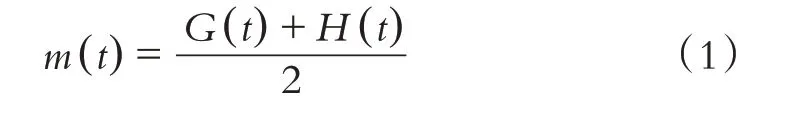
第四步，用原始数据减去均值包络线m( )t，得到中间序列l( )t：

第五步，判断中间序列l( )t是否还存在负的局部极大值和正的局部极小值，假如满足，说明该中间序列非本征模函数，需要继续重复上述步骤. 最后进行多次迭代，完成EMD分解，如图4所示.

图4 经验模态分解

2 基于人工神经网络的滑坡预测

2.1 人工神经网络原理

人工神经网络是指由大量的处理单元，也就是神经元互相连接而形成的复杂网络结构，是对人脑组织结构和运行机制的某种抽象、简化和模拟. 它是以数学模型模拟神经元活动，是基于模仿大脑神经网络结构和功能而建立的一种信息处理系统. 一般处理的序列具有非线性、非局限性、非常定性和非凸性这四个基本特征. 这里的非局限性就是模拟大脑的非局限性；非常定性是因为神经网络在处理信息时产生的各种变化；非凸性指系统在某个特定的状态函数下会产生多个极值以此来趋于多个较稳定的平衡状态，从而导致系统演化的多样性.

由EMD 分解后进行神经网络预测的技术路线如图5所示.

图5 技术路线图

神经元的组成结果如图6所示.

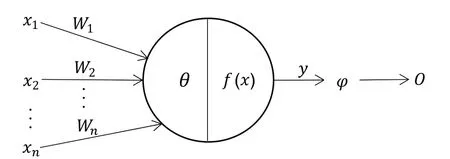
图6 神经元模型的基本结构

人工神经网络即是通过上述各变量来进行网络运算的，用公式表示为：

2.2 人工神经网络预测过程

第一步：准备数据集. 首先确定各个参数所表达的涵义：

(1)输入向量：X=(x1，x2，…，xi，…，xn)T；

(2)隐藏层输出向量：Y=(y1，y2，…，yj，…，ym)T；

(3)输出层输出向量：O=(o1，o2，…，og，…，ol)T；

(4)期望输出向量：D=(d1，d2，…，dg，…，dl)T；

(5) 输入层至隐藏层之间的权重矩阵：U=(u1，u2，…，uj，…，um)；

(6) 隐藏层至输出层之间的权重矩阵：W=(w1，w2，…，wi，…，wn)；

第二步：定义网络结构和激活函数：

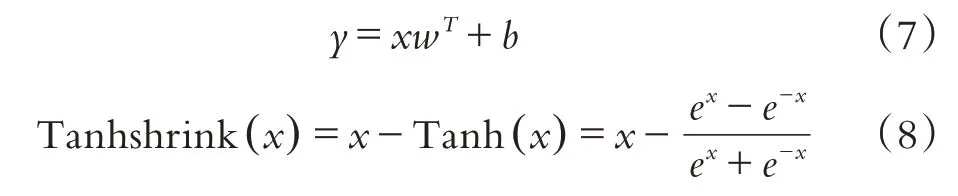
第三步：定义损失函数，本文使用最小平方误差函数：

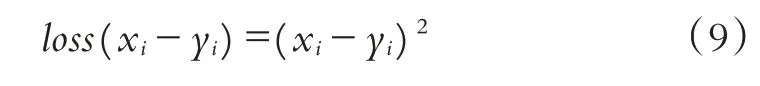
第四步：定义迭代优化算法，本文采用Adam 算法，该算法是一种可以代替传统随机梯度下降过程的一阶优化算法，能基于训练数据迭代地更新神经网络权重. 其实质是带有动量项的RMSprop，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率. 主要优点是经过偏执矫正后，每一次迭代学习率都有个确定范围，使得参数比较平稳.

第五步：迭代训练.首先计算前向传播网络；接着计算损失函数；然后反向传播更新参数；接着将上次迭代计算的梯度值清0；又反向传播，计算梯度值，更新权值参数；最后保存训练集和测试集上的损失函数以及准确率和训练模型.

第六步：画出原始曲线与神经网络拟合后的曲线.

第七步：画出损失函数在迭代的过程中的变化情况.

第八步：计算出均方根误差rmse和r2.

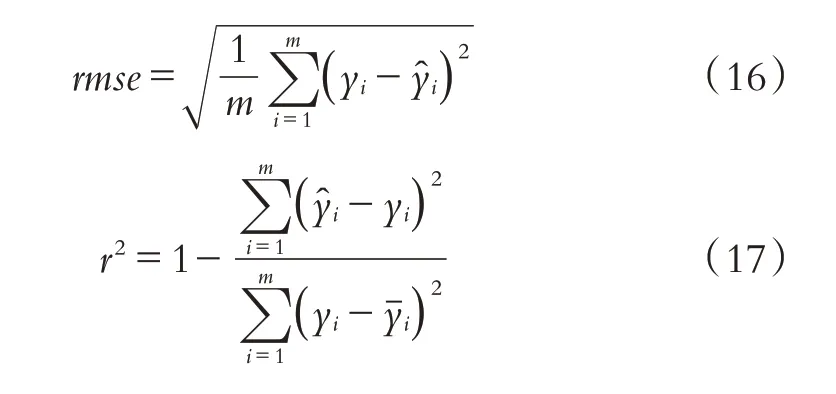
3 滑坡趋势预测分析

对Y1，1-Y1，102，…，Y1，10-Y10，102在进行图4 的EMD分解后，进行人工神经网络预测，一次输入一组Y值，输出预测值. 图7、图8 为选取展示的一组（Y1，1-Y1，102）.

图8 对残差项res的ANN预测

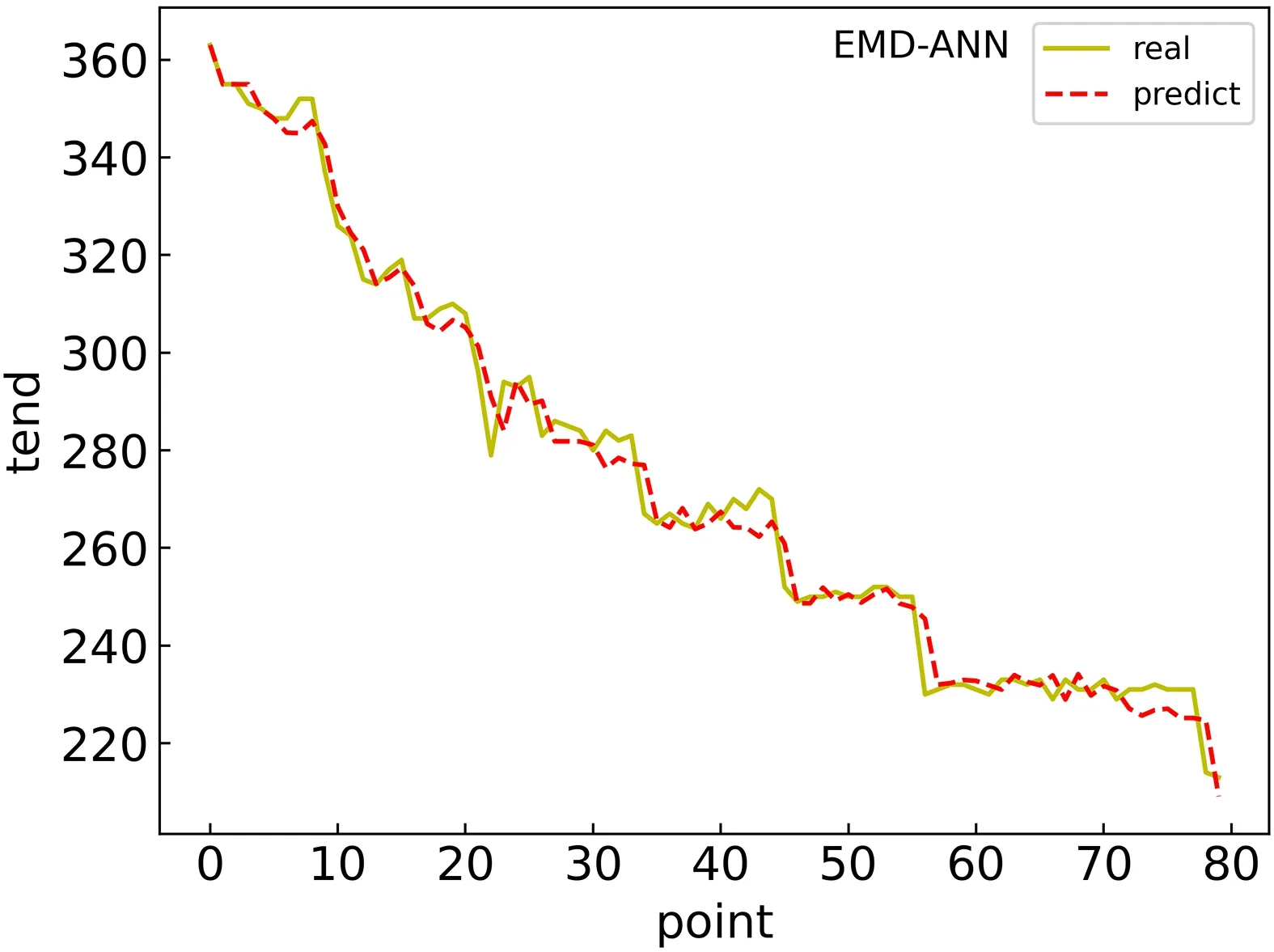
图9 对IMF1与res整合的ANN预测

最后，计算出十组数据的RMSE和r2，从表1 中可以看出，在进行经验模态分解后，极大地降低了原始数据的非平稳性，用分解后得到的平稳IMF分量对原始滑坡模拟数据进行预测，剔除滑坡模拟数据的干扰成分后，从而在预测数据样本时表现出较高的精度和稳定性.

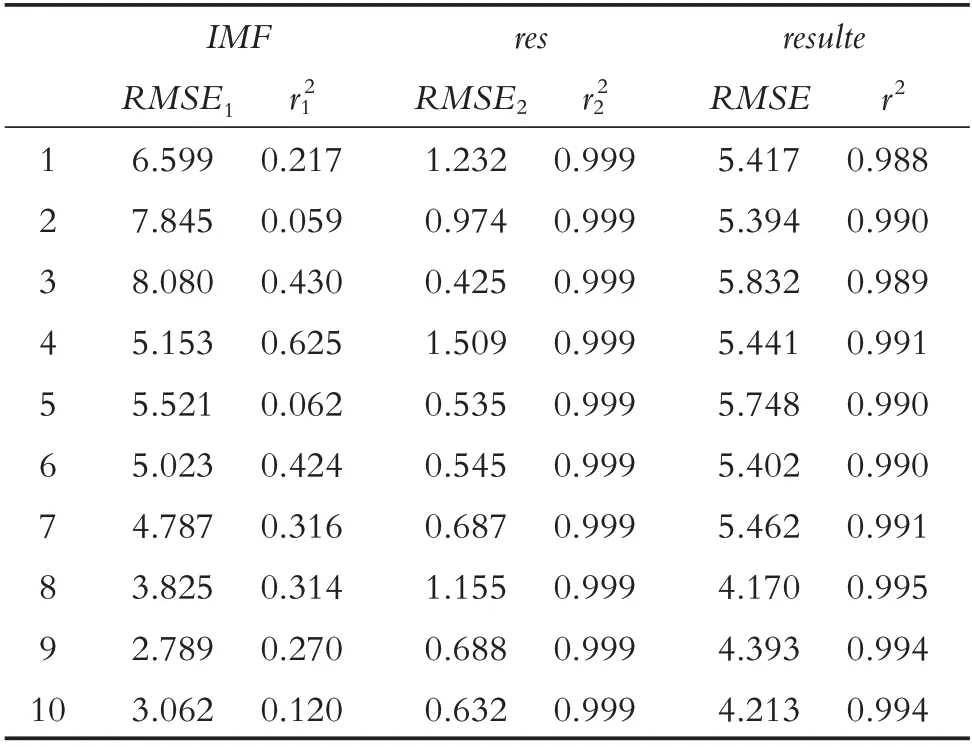
表1 预测结果

4 结论

（1）本文基于经验模态分解的人工神经网络预测滑坡趋势变化的方法，结合了经验模态分解和人工神经网络二者的优点，将原始滑坡模拟数据序列进行EMD 分解，降低了滑坡模拟数据的非平稳性，从而去掉了滑坡模拟数据中的干扰成分，用分解得到的IMF分量作为ANN 神经网络的输入变量进行预测，结果表现出较高的拟合精度及预测精度.

（2）本文通过实验模拟坡角为30°的后锋降雨的滑坡，未进行其位移预测，直接对其进行趋势预测，总体上，实验过程较为简单.

（3）对于滑坡破坏趋势的研究，在一些技术设备仪器方面还是有欠缺，使得实验结果不够完美，但是该预测模型作为神经网络的一种方法，适合于不同锋型降雨和不同坡角滑坡趋势预测.