基于ESO-GA多层次优化策略的减振器拓扑优化研究

盛 鹰，贾 彬，王汝恒，钟毅彬，吴时程

（1.西南科技大学土木工程与建筑学院，四川 绵阳 621000；2.西南科技大学工程材料与结构冲击振动四川省重点实验室，四川 绵阳 621000）

引 言

橡胶减振器因具有刚度易调节、形状设计自由、可吸收高/低频振动等优点，被广泛用于土木、机械、军工、航空、航海等行业的减振降噪中[1-4]。而刚度、阻尼系数、损耗系数等则是影响橡胶减振器减振效果的重要性能指标[5-7]。

圆柱形橡胶减振器因结构简单、加工方便、安装简便、规格多样，是工程中常用的一种形式，在建筑、桥梁、交通等对减振效能指标（如角位移、加速度传导比等）要求不高的工程领域中得到广泛应用。但对于振动工况下的精密仪器减振、文物防震预防性保护、运动载体中成像与测绘设备减振等对减振效果要求很高的领域，圆柱形橡胶减振器较难达到减振效能要求[8-10]。

为提高橡胶减振器的减振效果，除了优化减振器材料的胶料配方、工艺、材性等之外，不少学者研究了在特定的振动环境下橡胶减振器的几何形状对减振效果的影响。刘辉等[11]研究了“人”字型预弯柱体橡胶减振器在不同工况下的动刚度特性；鞠梓文等[12]研究了提高非等截面车辆橡胶减振器减振性能的影响因素；刘德宇[13]研究了列车用异型橡胶减振器的动刚度与等效阻尼等特性对列车安全性及舒适性的关系。

橡胶减振器的减振性能与胶料性能、几何形状、所处工况、被减振物的动力特性等密切相关，它们之间存在着复杂的非线性关系，难以通过普通的数学模型来描述。因此，学者们在设计橡胶减振器的几何形状时，大多采用经验方法，并将试验与数值模拟方法相结合，反复调整减振器的外形尺寸与中部镂空尺寸，使之满足被减振物在特定环境下的减振要求[14-16]。

在被减振物及其所受工况已确定的条件下，为快速确定橡胶减振器的几何形状与减振性能的关系，本文探究了一种多层次的优化策略，提出了一种使橡胶减振器具有最佳减振性能的拓扑优化结构设计方法。首先，基于渐进结构优化法（Evolutionary Structural Optimization，ESO）建立了橡胶减振器在指定工况下的拓扑优化模型；然后，将拓扑优化结果转化为可用参数度量的有限元模型，即建立基于APDL 参数化建模技术的有限元模型；最后，建立可量化的减振性能最优化目标函数，基于遗传算法（Genetic Algorithm，GA）与VC++对ANSYS 的二次开发技术，可快速求出使减振器具有最佳减振性能时所对应的最优几何参数解。本文的多层次拓扑优化策略为面向工程的结构优化设计提供了新思路。

1 减振器拓扑优化模型

1.1 结构减振原理的力学模型

三向减振装置的简化力学模型如图1所示。

图1 三向减振装置的简化力学模型

系统的振动可分解为竖直方向与水平方向的振动。选取中间支座的竖向位移y、被减振物的水平位移x和摆角θ为广义坐标。

先将上部结构视为整体，由式(1)可计算在外荷载P2(t)作用下中间支座的动力响应y：

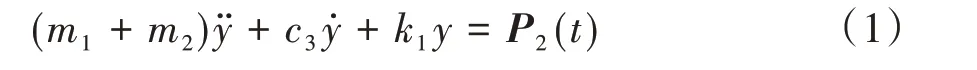
其中：m1、m2分别为被减振物和减振装置的质量。

上部结构的动能T、势能V和耗能函数D为：

其中：g为重力加速度。

取Lagrange 函数L=T-V，并将式(2)代入Lagrange方程：

即可建立系统运动微分方程，进而求出被减振物的动力响应x(t)和θ(t)。

1.2 结构拓扑优化的数学模型

结构拓扑优化问题可定义为确定某部分材料在设计空间中存在与否的问题，即：

其中：Ω 为初始给定设计区域，Ωs为实体材料所占的区域，Ω/Ωs为孔洞所占的区域。

拓扑优化的数学模型可表示为：

其中：f(u)表示目标函数。

拓扑优化的基本步骤为[17-18]：

（1）确定足够大的设计区域并明确设计变量、目标函数、边界条件；

（2）对结构作有限元分析，计算设计变量变化对目标函数变化的敏感度；

（3）用合适的优化方法计算当前的设计变量的新值；

（4）根据终止准则判断是否收敛和终止迭代；

（5）进行拓扑优化后处理，得到最优拓扑的形式。

2 ESO-GA多层次优化策略

2.1 ESO方法基本步骤

运用渐进结构优化法（ESO）进行结构拓扑优化，以应力作为优化准则，即基于应力水平来删除材料，其目标就是通过贯穿整个结构产生一个更均匀的应力水平来获得一个更有效的设计。

对于各向同性材料的拓扑优化问题，一般采用式(6)所示的Von Mises应力作为应力准则：

ESO方法的基本思想为：在某一局部，假设低应力的材料处于没有充分利用的状态，于是将该局部材料删除。如此逐渐地删除低应力的材料，逐渐更新设计，使经过优化后的结构应力水平变得更均匀。在这种优化准则下，通过逐渐去掉结构中的低应力材料，减小结构中应力分布的差异，使剩下的结构能更有效地承担荷载，进而使应力尽可能均匀地分布。

运用ESO 方法进行结构拓扑优化设计的流程如图2所示。

图2 ESO方法的计算流程图

2.2 GA算法基本步骤

当基于ESO 方法的结构拓扑优化完成后，将拓扑优化结果转化为可用参数度量的有限元模型，接下来用遗传算法（Genetic Algorithm，GA）[19-21]对结构的几何参数作进一步的精细化优化。

定义加速度传导比[22]为优化目标函数，如式（7）所示：

其中：η(X)为加速度传导比函数，X为各个变量构成的向量组，a0为减振装置底部受到的加速度，a1为被减振物顶部产生的加速度。

GA 是一类可用于复杂系统优化计算的鲁棒搜索算法，其基本特征是利用群体进化，即在求解的过程中，通过种群不断优化，从而找到满意解或最优解。本文针对橡胶减振器的拓扑优化结构，运用GA算法优化计算的主要步骤为：

（1）将待优化变量符号化，用二进制符号0 和1所组成的二值符号集{0，1}进行编码。选取橡胶减振器的4个参数为待优化参数：上表面外径D1、上表面孔径D2、下表面外径D3、下表面孔径D4，即决策向量D=[D1，D2，D3，D4]T。

将每个变量Di(i=1，2，3，4)用长度为l的二进制编码表示。假设某一变量Di的取值范围是[Umin,Umax]，则该变量总共可产生2l种不同的编码。于是，二进制编码的编码精度δ为：

设某一变量Di的二进制编码为：blbl-1,…,b2b1，则该变量对应的解码值di为：

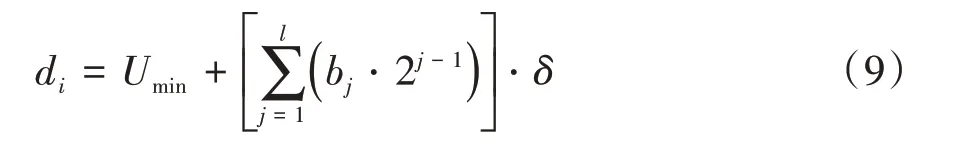
（2）初始化群体。遗传算法的运算过程是一个反复迭代过程，第n代群体记作P(n)，则设置进化代数计数器n= 0，设置最大进化代数N，并随机生成M个个体作为初始群体P(0)。

（3）运用VC++对ANSYS 的二次开发技术计算群体P(n)中各个个体目标函数值（加速度传导比）。

为实现VC++对ANSYS 的二次开发，其关键问题是解决VC++调用ANSYS 的APDL 命令流的接口问题。这一步的实现过程分为4小步：

①用VC++生成APDL 命令流文件，该命令流文件包含参数化建模、求解、结果后处理的全过程；

②实现VC++对ANSYS 的自动调用，即：VC++自动启动ANSYS，ANSYS 启动后自动读入第①步生成的APDL 命令流文件，完成建模、求解、结果输出的全过程，每一次计算完毕后退出ANSYS；

③在ANSYS启动后自动读入指定路径的APDL命令流，完成结构建模、计算分析和结果输出。

④VC++检测到ANSYS 进程退出后，从指定路径读入ANSYS 计算输出的结果，该结果即为GA 算法中群体P(n)中对应个体的目标函数值（加速度传导比）。

在VC++中可以利用CreateProcess 函数来创建一个进程去执行其他程序，而且可以设置该进程的优先级。以ANSYS 18.0 为例，用VC++启动ANSYS的关键代码为：

为了使ANSYS18.0 启动后自动读入指定路径的APDL 命令流（假设命令流文件的存储路径为E:program.txt），则只需在ANSYS 安装目录下找到文件“start180.ans”并打开该文件后写入以下代码：

INPUT,′program′,′txt′,′E:′,0

这样，当VC++程序运行后，程序就能自动启动ANSYS 并读入存储于“E:program.txt”的APDL 命令流，进而自动完成结构建模、计算分析和结果输出。

（4）依次进行选择运算、交叉运算和变异运算，分别将选择算子、交叉算子和变异算子作用于群体，于是得到下一代群体P(n+ 1)。

（5）若nN，则终止计算，并将进化过程中所得到的具有最大适应度的个体作为最优解输出。

由于遗传算法是一种概率搜索算法，因此在运算前需要预先设置群体大小M、遗传算法的终止进化代数N、交叉概率pc和变异概率pm4个运行参数。

本文运用GA算法优化计算流程如图3所示。

图3 GA算法的计算流程图

2.3 ESO-GA多层次优化步骤

ESO-GA多层次优化的步骤如图4所示。

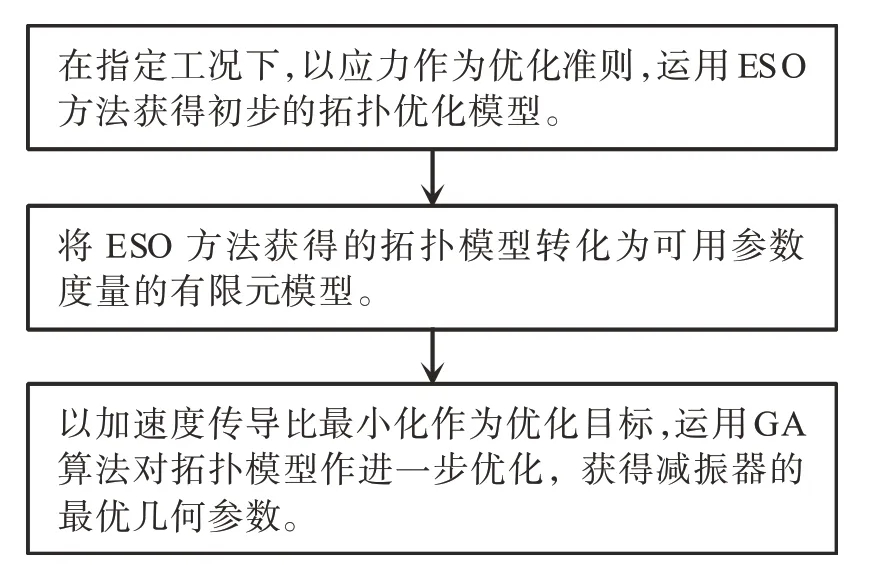
图4 ESO-GA多层次优化流程图

3 计算结果及分析

3.1 ESO优化结果

设计橡胶减振器的初始拓扑形状为圆柱体。选用的橡胶材料硬度为70 A，其压缩弹性模量为7.34 MPa，泊松比为0.47。在竖向正压力作用下，分别设置单元删除率为15%、35%、55%、75%、85%和95%时，得到的拓扑优化结果如图5所示。

图5 ESO-GA多层次优化流程图

根据橡胶减振器的应力水平，最终选取单元删除率为85%的拓扑模型，并将其转化为可用参数度量的有限元模型，如图6 所示。图6（a）所示为ESO算法拓扑优化模型，该模型外形呈“上小下大”形状，且中间有非等截面通孔。虽然ESO 算法能得到最优拓扑结构的大致形状，但该拓扑优化模型边界粗糙，特征尺寸不易表征。为方便进行APDL 有限元参数化建模，根据ESO 算法得到的大致拓扑形状，对模型边界进行了光滑和规则化处理，如图6（b）所示。并选取橡胶减振器的4个尺寸为特征尺寸：上表面外径D1、上表面孔径D2、下表面外径D3、下表面孔径D4。图6（a）和图6（b）的形状大致相似，从图6（a）到图6（b）的模型转化过程是人为观察后作出的合理简化，是后面运用GA 算法进行橡胶减振器特征尺寸优化的前提和基础。后面将运用GA 算法求出使橡胶减振器在指定工况下具有最佳减振效能（即加速度传导比最小）所对应的最优特征尺寸值。

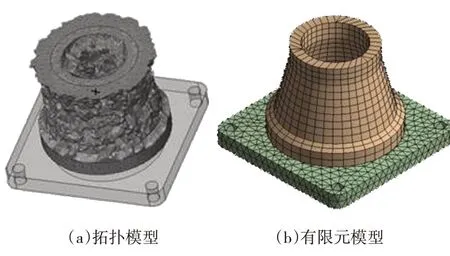
图6 拓扑模型与有限元模型的对应

建立如图7 所示的有限元模型，图中底部为4个橡胶减振器，减振器与支撑台面固连，支撑台面上放置被减振物（质量为75 kg，高宽比为1∶1），被减振物与台面的摩擦系数为0.15。在减振器底部施加水平方向半正弦冲击荷载如下：

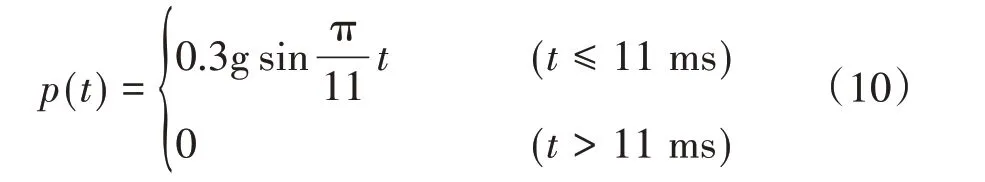
图7 减振系统有限元模型

拓扑优化前、后，被减振物顶面中心节点的加速度-时间曲线、加速度传导比-时间曲线分别如图8、图9所示。

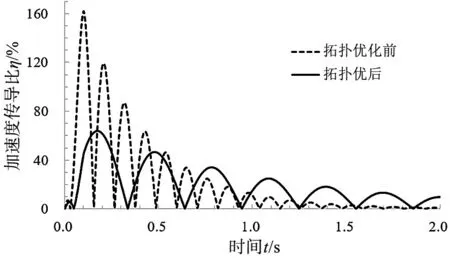
图9 被减振物顶面中心的加速度传导比-时间曲线

从图8 和图9 可知，拓扑优化前，被减振物顶面中心节点的最大加速度为4.77 m/s2，最大加速度传导比为161.98%，被减振物顶面加速度被显著放大，橡胶减振器未起到减振作用；拓扑优化后，被减振物顶面中心节点的最大加速度为1.87 m/s2，最大加速度传导比为63.30%，被减振物顶面加速度小于减振器底部加速度，橡胶减振器起到了良好的减振作用。

3.2 GA优化结果

为进一步提高橡胶减振器的减振效果，接下来用GA 算法对其外形与内孔尺寸作进一步优化。选取橡胶减振器的4 个参数为待优化参数：上表面外径D1、上表面孔径D2、下表面外径D3、下表面孔径D4。

在计算中，为防止早熟收敛，运用了隔离小生境技术，即将遗传算法的初始群体分为相互独立的多个子群体，各个子群体独立进化，其进化快慢取决于子群体中个体的平均适应度水平。

采用3 个子群体进行独立并行计算，每个子群体各包含10 个个体。由程序随机生成二进制代码对群体初始化。设置交叉概率为0.167，变异概率为0.040。以加速度传导比最小化作为优化目标，各子群体的进化曲线如图10所示。

图10 3个子群体进化曲线

子群体1、子群体2 和子群体3 优化得到的最大加速度传导比分别为30.1%、28.1%和28.2%。子群体2 仅进化了4 代就收敛到了减振器具有最优减振性能所对应的最优几何参数解，此时，被减振物顶面的偏转角-时间曲线如图11所示。

图11 减振器最优拓扑结构的偏转角-时间曲线

由图11 可知，被减振物顶面的最大偏转角为17.20′。结果表明，经GA 算法优化后得到的橡胶减振器对所研究的被减振物及其所处的工况环境具有优异的减振性能。

算例表明，本文基于ESO-GA 多层次优化策略对减振器进行拓扑优化的方法是可靠的。

4 结 论

提出了一种使橡胶减振器具有最佳减振性能的拓扑优化设计方法（ESO-GA 方法），并通过算例验证了该方法的有效性，得到结论如下：

（1）本文提出的ESO-GA 多层次优化策略将ESO 方法的拓扑优化与GA 算法的高效搜索结合起来，有很高的鲁棒性。其求解不依赖具体问题，优化能力和效率都有非常明显的优势。

（2）GA 算法的优越性不是独立的，在本文的算例中，将它与有限元软件的二次开发结合起来，采用参数化编程，从建模、加载求解、结果提取到优化设计都无须人工干预，设计效率显著提高。同时，GA 算法的引入，改变了传统的优化设计观念，其优化结果既不会过于“危险”，也不会过于“保守”，是一种经济的设计方法。本文建立的ESO-GA多层次优化策略对其他结构的动力响应优化设计也有一定的借鉴意义。