边缺陷诱导的双层锯齿型石墨烯纳米带能隙*

韩 超，龙 文

（首都师范大学物理系，北京 100048）

0 引 言

2004 年，英国曼彻斯特大学物理和天文学系教授Novoselov 等［1］用机械剥离方法成功制备出了石墨烯，并于2010 年获得了诺贝尔物理学奖.石墨烯晶格由2 个不等价子格构成，导带和价带在2 个不等价的Dirac 点以圆锥形相切［2-3］，这2 个Dirac 点手性相反，组成一个时间反演对，这使得二维石墨烯具有独特的电子特性［4-8］，如具有半整数量子霍尔效应［9］，没有背散射［10］等.石墨烯独特的电子结构使得其可以通过栅压［11］、磁场调控［12-14］、化学掺杂［15］和边缘缺陷［16］修饰其性能.

双层石墨烯［17-21］是由2 层石墨烯经范德华力耦合在一起，每层含2 个子格，分别称为A 子格和B 子格，通常有2 种堆叠形式，AA 和AB 堆叠（即伯纳尔形式堆叠）.双层石墨烯在许多方面表现出与单层石墨烯截然不同的性质，如量子霍尔效应［14，17］、边态［22］、弱局域态［23］、无序［24］和最小电导率［25-26］以及其他有趣现象［27-29］.通过外加电场［30-31］等方式可以连续调整零能量点附近的带隙，改变电荷密度分布［17］，诱导低密度铁磁性［32］.

当顶层石墨烯相对于底层石墨烯层旋转一定角度时会形成转角石墨烯，可显著改变双层石墨烯的电子能带.转角石墨烯所具有的扭转自由度进一步丰富了双层石墨烯的物理性质，使转角石墨烯成为探索电子奇特性质［33-37］、光学［38-41］以及范德华异质结构热行为［42-43］的重要元件.转角石墨烯的一个显著例子是魔角，即其以一个小扭角（如1.08°）错位，在费米能级附近具有平带［33，35，37］.最近的实验已经证实，这些扭角诱导的平带，产生了非常规的超导性［33］以及相关（莫特）绝缘状态［34］.这些发现激发了大量的理论和实验工作，试图阐明魔角石墨烯潜在的物理性质和应用［35，38-39，44-50］.转角石墨烯可以作为高阶拓扑绝缘体的有力候选材料［48］.

石墨烯纳米带是一种新型量子线，既可看作是条带状小尺寸的石墨烯，也可看作是纵向切割碳纳米管的产物，是一种新型的准一维碳纳米材料［51-53］.因其特殊的边缘限域效应，使石墨烯纳米带比石墨烯更灵活可控［54］，较高长宽比的结构特点使得电子在石墨烯纳米带中的横向移动受限，从而只能纵向移动导致其具有半导体的性能［55-56］.研究表明，石墨烯纳米带的边缘构型、宽度和层数对其电学性能、磁学性质和化学性质等产生决定性影响［57-58］.因此，石墨烯纳米带是一种极具应用潜力的新型纳米材料.

双层石墨烯纳米带是由单层石墨烯纳米带通过一定的堆叠方式形成的准三维结构系统，包括AA 和AB 堆叠.类似地，用纳米带的边界形状来定义双层石墨烯纳米带，即分为锯齿型和扶手型.不考虑电子自旋时，扶手型纳米带的电子特性和纳米带的宽度有关，宽度为3n+2 时，体系呈金属性，其余呈半导体性；而锯齿型纳米带的能带在费米面附近简并，体系只呈金属性［3，59-60］，这在一定程度上限制了双层锯齿型石墨烯纳米带在量子器件中的应用.

边缘态因其独特的物理性质，在介观输运中十分重要，这使得边缘态在固态电子学二维系统中成为研究的一个热点.改变纳米带边态能量［61-63］以及边缘无序［64］均会对石墨烯纳米带能带结构产生影响.对于锯齿型石墨烯纳米带而言，局域态一直存在于Dirac 点附近.因此，锯齿型石墨烯纳米带体现出类金属行为，这些特性与传统的半导体量子线的性质十分不同，这就为裁制输运和光学性质的石墨烯纳米带提供了可能［65］.因此，本文主要利用无相互作用的紧束缚模型，研究边界线缺陷对双层锯齿型石墨烯纳米带能谱及边态的影响.

1 模型和公式

双层锯齿型石墨烯纳米带堆叠类型和含线缺陷的单胞如图1 所示.t0是层内最近邻原子间相互作用，t1是上层A 原子与垂直下层B 原子间的层间相互作用，t2是上层六角中心B 原子与下层最近邻A原子间的层间相互作用，t3和t4分别是A 原子间和B原子间的最近邻层间相互作用.本文统一使用蓝色表示上层，黑色表示下层.带宽沿X方向分为N层，每层含一个锯齿链，有2 类格点原子，一类位于A 格点，另一类位于B 格点.每个单胞含4N个格点，纳米带沿Y方向具有周期平移不变性.

考虑如图1（c）和（d）所示的单胞，并让其两端向两侧沿Y方向无限延伸［66-67］.含边界线缺陷的无限长锯齿型双层石墨烯纳米带满足的等效差分方程为

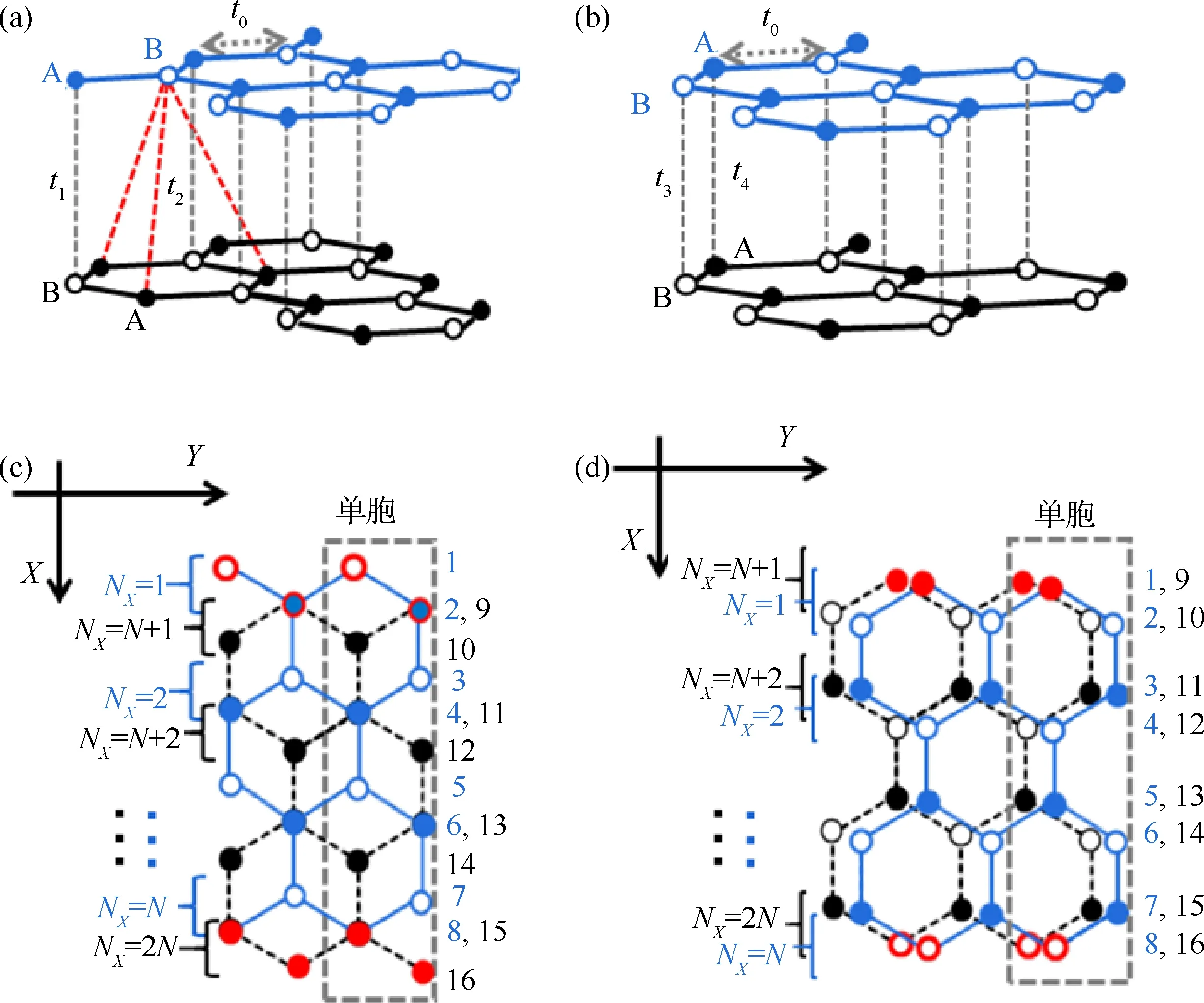
图1 双层锯齿型石墨烯层间相互作用及单胞

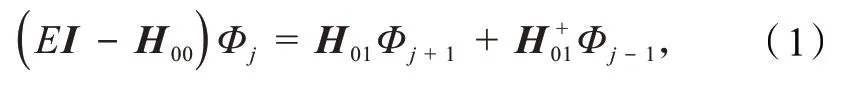
式中

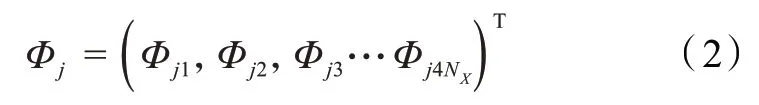
是双层锯齿型石墨烯纳米带的单胞格点波函数，T表示转置，E表示电子能量，H00和H01分别表示占位能矩阵和交叠积分矩阵，I为单位矩阵，这3 个矩阵都是4N× 4N的.利用双层锯齿型石墨烯纳米带沿Y方向具有平移不变性，考虑到波函数具有Bloch 波形式，可将式（1）改写为

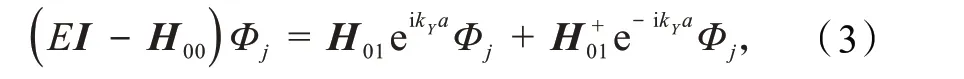
式中a= 0.246 nm 是石墨烯的晶格常数.求解上述等效差分方程可得到双层锯齿型石墨烯纳米带的能带结构和能量本征波函数.

考虑一个含双层锯齿型石墨烯纳米带的量子输运系统，如耦合到左、右导线的含缺陷AB 堆叠双层锯齿型石墨烯带（图2）.在最近邻紧束缚模型近似下，体系的总哈密顿量为

图2 耦合到左、右导线的含缺陷AB 堆叠双层锯齿型石墨烯带

式中：第1 项H中心区表示中心区AB 堆叠含缺陷双层锯齿型石墨烯纳米带哈密顿量，在紧束缚近似下可表示为

在格林函数范式下，双层锯齿型石墨烯纳米带的透射概率为

式中：η→0+，I为单位矩阵，ΣrL和ΣrR分别表示中心区与左、右导线耦合的延迟自能.

体系的局域态密度（ρDOS）为

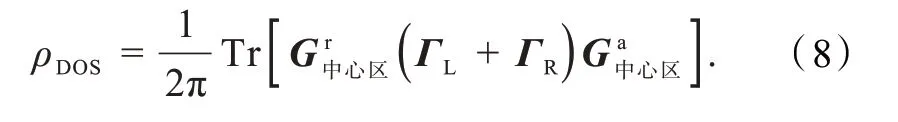
2 计算与讨论

本文研究2 种堆叠类型的双层锯齿型石墨烯纳米带的能带结构、导带底单胞格点波函数、透射概率和局域态密度.

2.1 AA 堆叠双层锯齿型石墨烯纳米带

AA 堆叠双层锯齿型石墨烯纳米带的能带结构如图3 所示.首先分析边界线缺陷对能带结构的影响.由于层间原子A（B）-A（B）之间的跃迁势，打破了单层石墨烯的空间对称性，使得其能带二重简并被解除，能带分裂成4条，能带分裂的程度是上下2 层间A（B）-A（B）之间的跃迁能.tA(tB)表示上（下）边界线缺陷层间跃迁系数，ul，A(ul，B)表示各层上（下）边界线缺陷格点占位能系数.当只改变体系上边界A 子格的层间跃迁系数，且设定tA=−15，则次价带顶和次导带底平带部分的色散关系会改变，在费米面附近打开一个能隙；当改变层间跃迁系数的同时改变边界线缺陷的占位能系数，即设定u1，A=u1，B=−0.3，u2，A=u2，B= 0.3，可知4 条平带的色散关系均可以被改变；当继续增大占位能系数绝对值，即设定u1，A=u1，B=−0.8，u2，A=u2，B= 0.8，导带底和价带顶平带部分更加远离费米面，弯曲程度增大.由此可知，通过改变边界线缺陷的层间跃迁值，能够打开AA 堆叠双层锯齿形石墨烯纳米带的一个能隙，并且如果同时改变合适的占位能，会增大能隙的宽度，能隙的宽度受占位能严格调控.

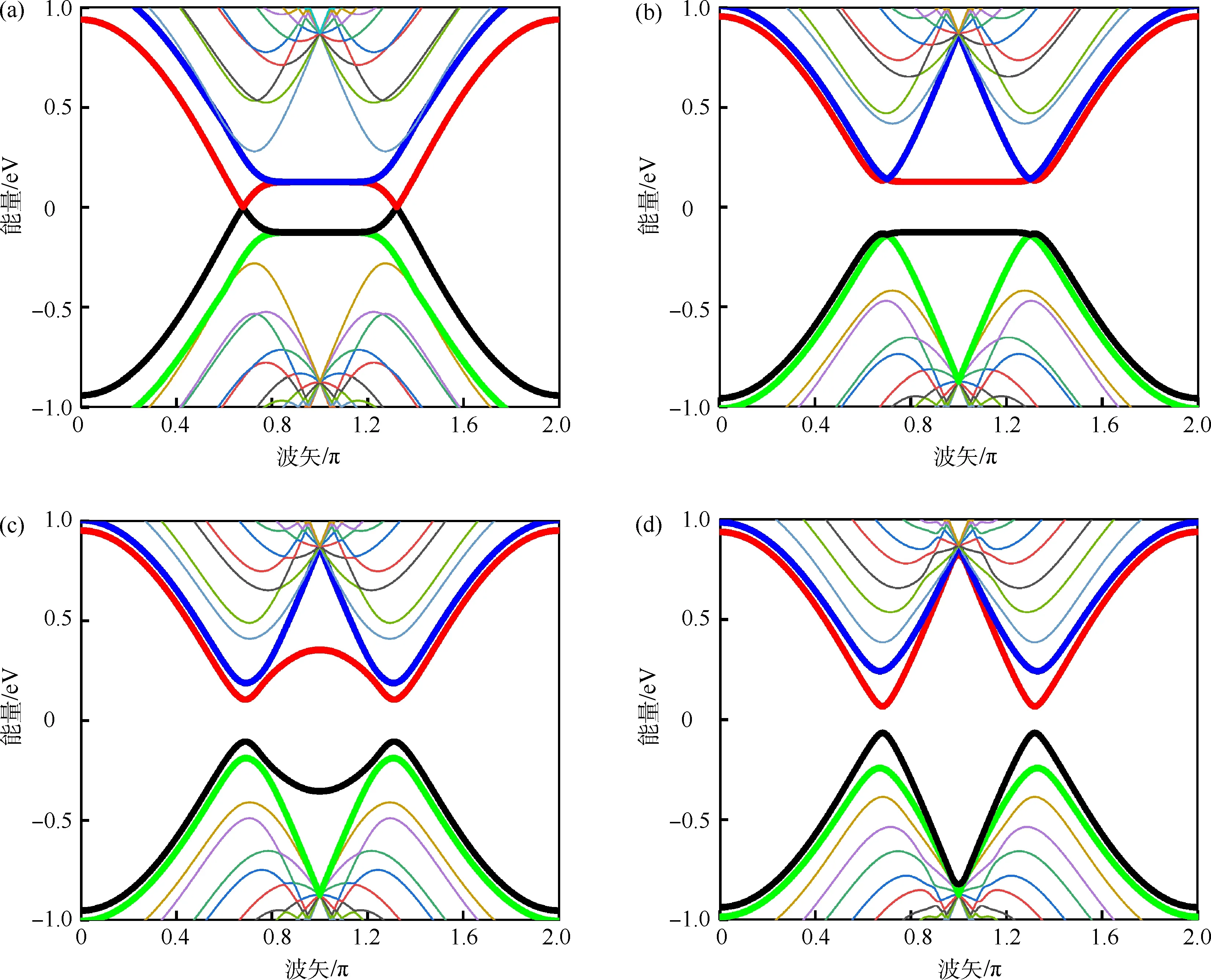
图3 AA 堆叠双层锯齿型石墨烯纳米带的能带结构

AA 堆叠双层锯齿型石墨烯纳米带导带底单胞格点波函数模随纵向波矢的演化如图4所示.本文给出了导带底的单胞格点波函数的模与波矢kY的具体关系，每一种条件展示3 个波矢，每幅图中各小图从上到下依次表示波矢kY= 0.67π、0.80π和0.90π，X轴为单胞格点位置.无缺陷时，当kY从0.67π（Dirac点附近）到π 时，电子逐渐占据边态，当kY=π 时，电子完全占据边态.而如果改变边界层间跃迁值时，会使电子呈现单边占据；当占位能绝对值较大时，电子边态占据不明显，基本呈现均匀分布.并且，本文研究了导带底和价带顶波函数分布情况，显示在无缺陷和只改变边界层间跃迁时，导带底和价带顶的波函数分布情况是一致的，而如果改变占位能后，即设定占位能符号相反时，导带底和价带顶的波函数分布情况会呈现上层和下层相反的特点.由此可知，边界层间跃迁和占位能数值会影响电子边态占据，但当占位能较大时对边态影响不大，同时，占位能还会影响电子在上层或下层的分布情况，这取决于上层或下层占位能的符号.

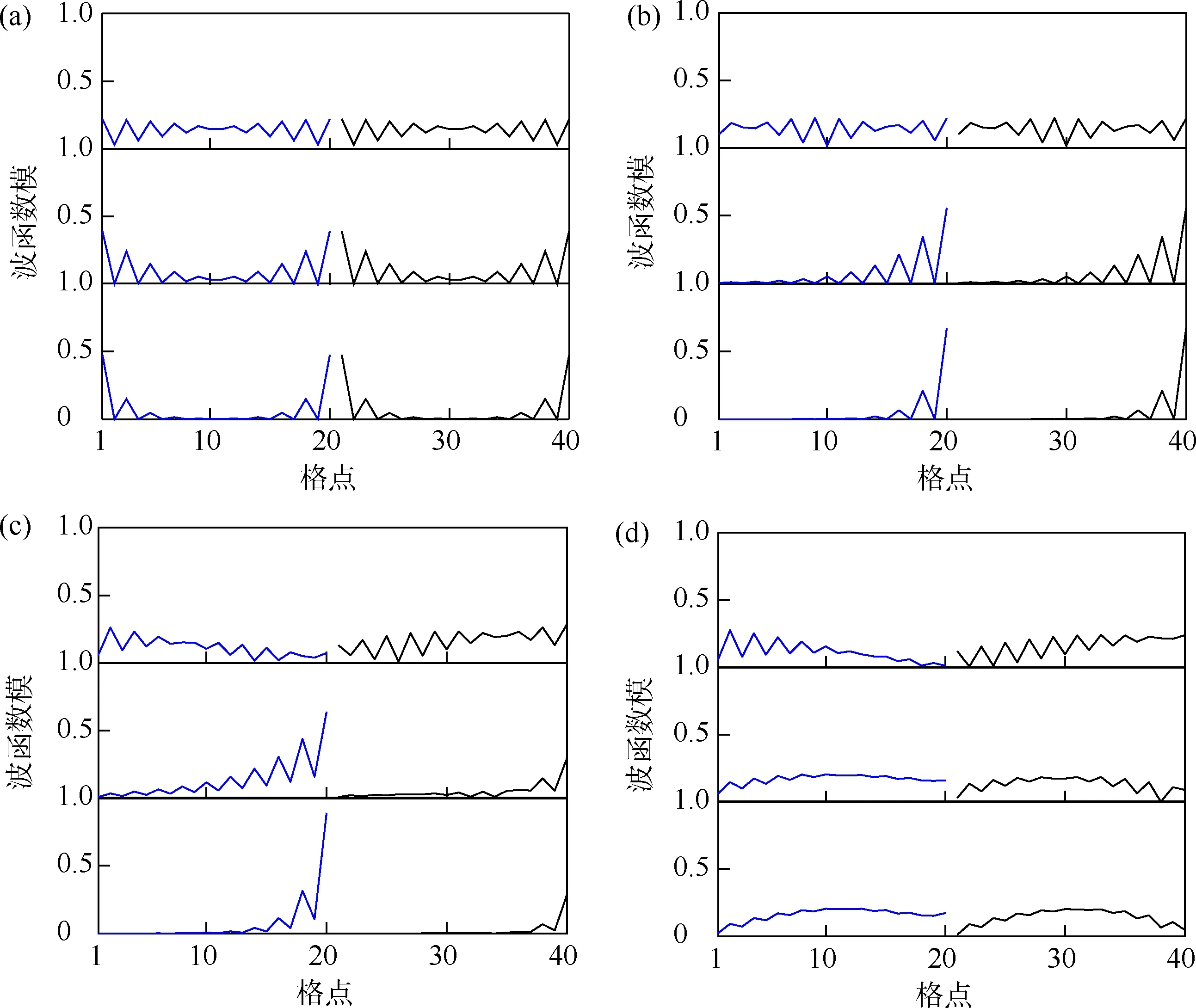
图4 AA 堆叠双层锯齿型石墨烯纳米带导带底单胞格点波函数模随纵向波矢的演化

AA 堆叠双层锯齿型石墨烯纳米带透射概率和局域态密度如图5 所示.对于无缺陷情况而言，AA堆叠双层锯齿型石墨烯纳米带在E=0 附近的局域态密度产生了尖峰，这主要是因为费米面附近平带的作用，因为体系横向子带的受限，可以在透射概率分布图上观察到平台.当改变层间跃迁系数或者同时改变层间跃迁系数和占位能系数，透射概率和局域态密度在E=0 附近的范围内为0，说明此时对应的重合能带被打开.

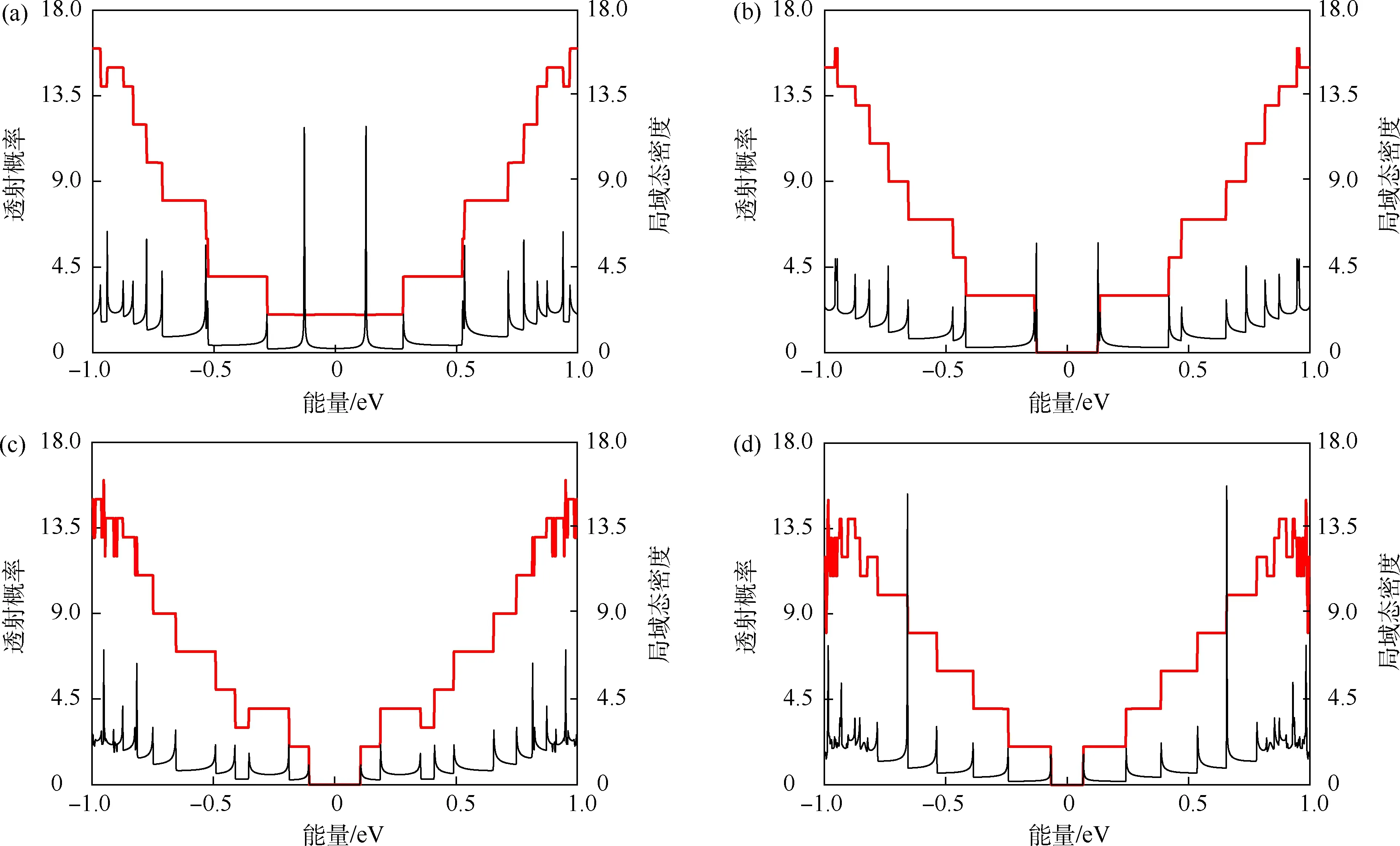
图5 AA 堆叠双层锯齿型石墨烯纳米带透射概率和局域态密度

2.2 AB 堆叠双层锯齿型石墨烯纳米带

AB 堆叠双层锯齿型石墨烯纳米带的能带结构如图6 所示.首先分析边界线缺陷对能带结构的影响，无缺陷AB 堆叠双层锯齿形石墨烯能带结构与单层锯齿型石墨烯纳米带的能带结构相似，只是AB 堆叠的双层锯齿形石墨烯纳米带能带在费米面附近存在4 条无能隙模连接导带和价带，即在费米面附近存在4 条平带；通过改变体系边界占位能，设上层上边界A 子格和下边界B 子格占位能系数为u1，A=u1，B=−0.5，下层上边界A 子格和下边界B 子格占位能系数为u2，A=u2，B= 0.5，在费米面附近打开1 个能隙，但此时能隙的值较小；当上层和下层上边界A 子格线缺陷占位能系数为u1，A=u2，A=−0.3，上层和下层的下边界线缺陷B 子格占位能系数为u1，B=u2，B= 0.3，打开的能隙宽度较之前增大；继续增大占位能系数，当u1，A=u2，A=−0.8，u1，B=u2，B=0.8 时，平带的弯曲程度较之前增大，说明边界线缺陷占位能影响费米面附近平带部分的弯曲程度，且费米面附近打开的能隙宽度也增大.由此可知，边界线缺陷的占位能会改变费米面附近能带的弯曲程度，并且通过改变合适的占位能符号和数值，可以在费米面附近打开能隙，能隙的宽度受占位能绝对值影响.

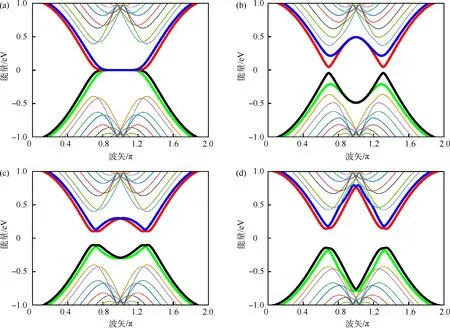
图6 AB 堆叠双层锯齿型石墨烯纳米带的能带结构

AB 堆叠双层锯齿型石墨烯纳米带导带底单胞格点波函数模随纵向波矢的演化如图7 所示.本文给出导带底的单胞格点波函数模与波矢kY的具体关系，每一种条件展示3 个波矢，每幅图中各小图从上到下依次表示波矢kY= 0.67π、0.80π和0.90π，X轴为单胞格点位置.当kY从0.67π（Dirac 点附近）到π时，对于无缺陷情况，电子占据分布较为均匀；随着波矢的增加，当kY= 0.80π 时，改变边界缺陷的占位能，会使电子占据边态的优势增强，通过研究价带顶的电子占据表明，可以通过改变占位能符号来改变电子在上下层的分布情况；继续增大边界占位能绝对值会使边态占据概率降低，当kY= π 时，边态占据优势最明显.由此可知，改变边界线缺陷占位能，可以调控电子分布占据边态优势，从而打开单边量子通道，为双层石墨烯半导体元件的应用提供了基础.

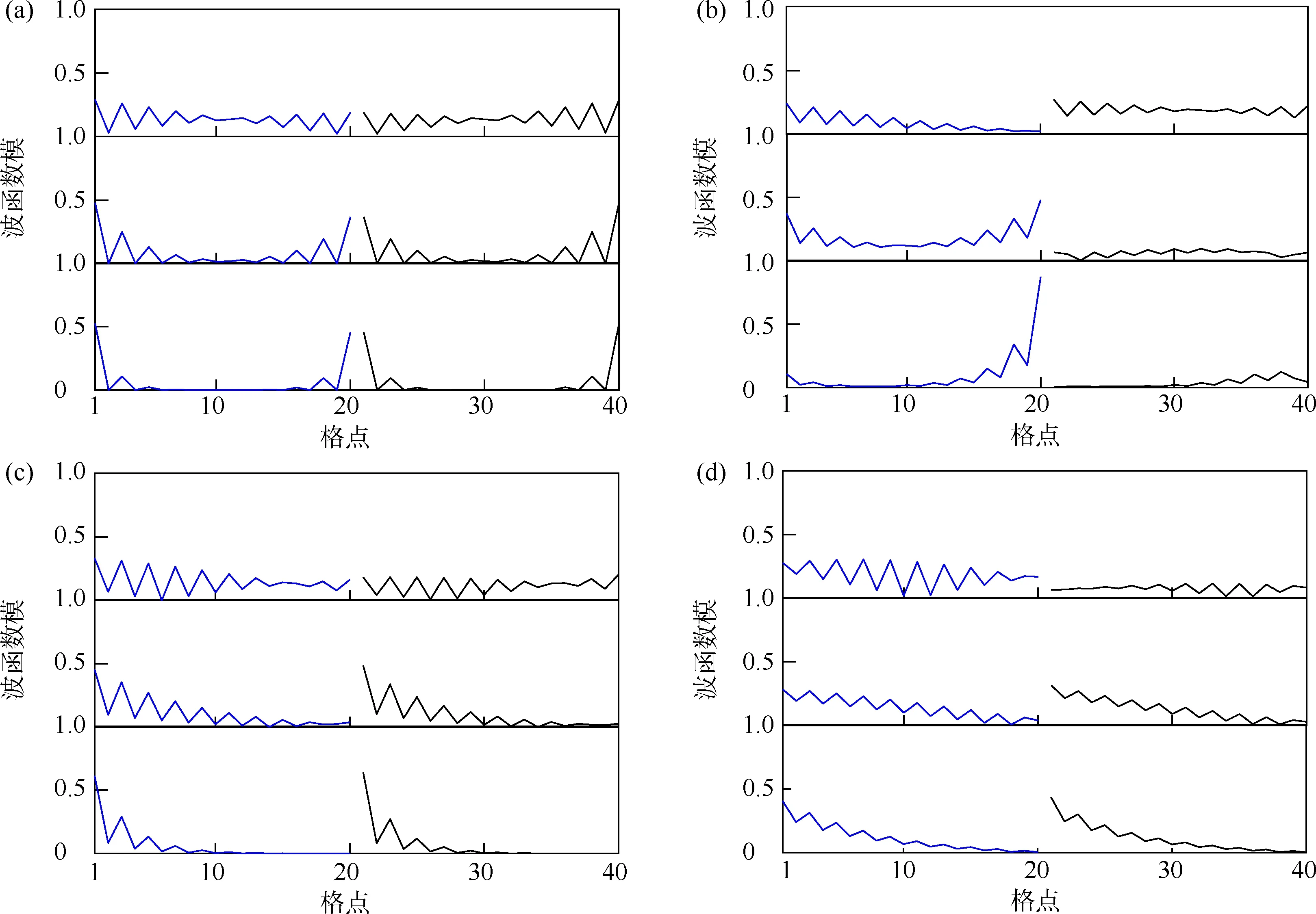
图7 AB 堆叠双层锯齿型石墨烯纳米带导带底单胞格点波函数模随纵向波矢的演化

AB 堆叠双层锯齿型石墨烯纳米带透射概率和局域态密度如图8 所示.对于无缺陷情况而言，AB 堆叠双层锯齿型石墨烯纳米带在E=0 附近的局域态密度也会有尖峰的产生，这依然归因于重合平带的贡献，同样地，可以在透射概率关系图上观察到平台.而改变层间跃迁系数或者同时改变层间跃迁系数和占位能系数时，透射概率和局域态密度在E=0 附近的范围内为0，说明此时能够打开一个能隙.

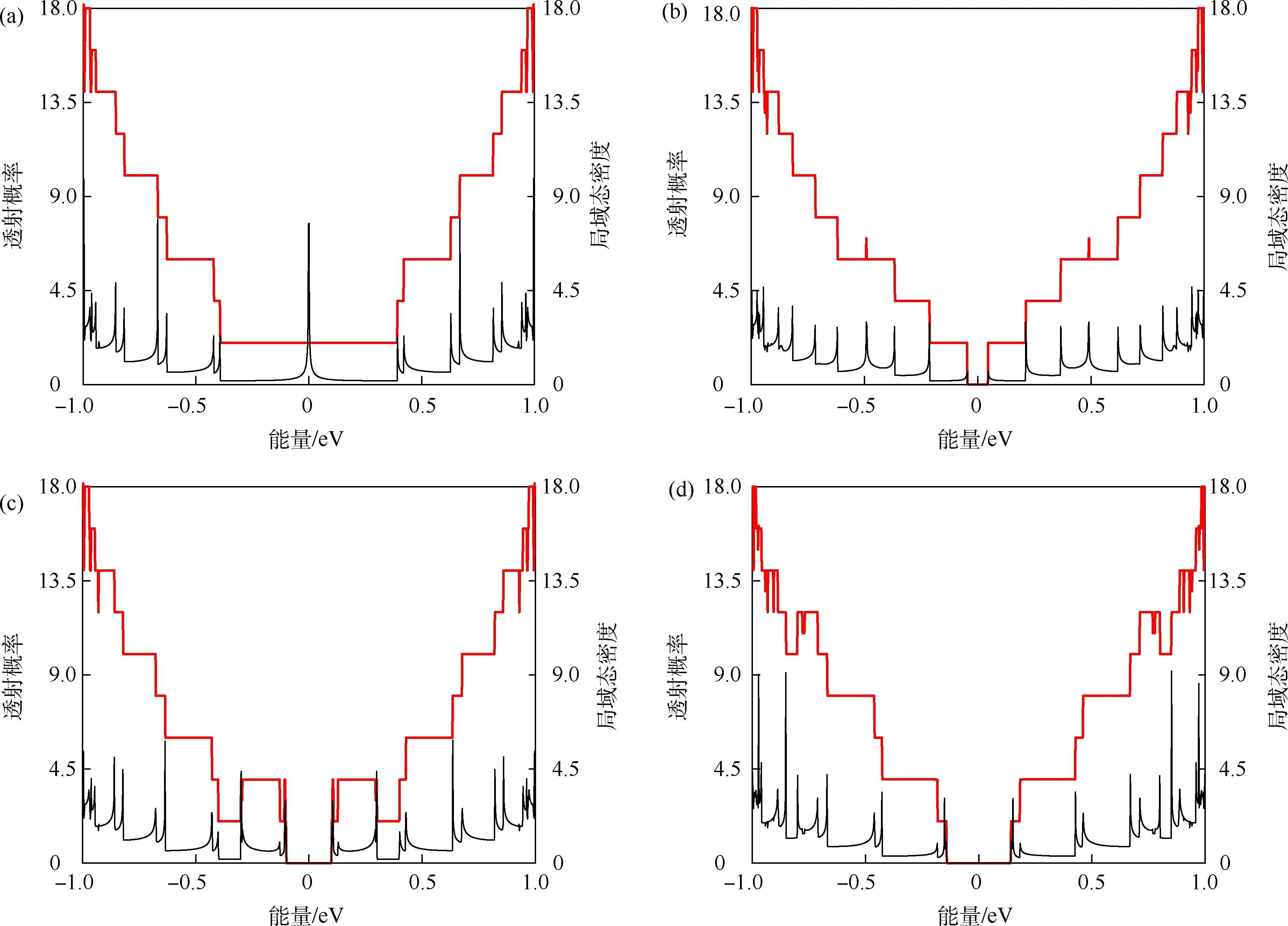
图8 AB 堆叠双层锯齿型石墨烯纳米带透射概率和局域态密度

3 结 论

根据单电子紧束缚近似模型，利用有限差分法，本文不仅计算了不同堆叠类型无限长双层锯齿型石墨烯纳米带的能谱及格点波函数，而且计算了两端口双层锯齿型石墨烯纳米带的局域态密度和透射概率，研究了体系上下2 条边界子格线缺陷的占位能和层间跃迁积分对纳米带能谱和边态的影响.研究表明：对于AA 堆叠，双层上边界A 子格和下边界B 子格缺陷占位能可调控导带底和价带顶平带色散关系，层间跃迁积分可调控次导带底和次价带顶的平带色散关系，打开体能隙，合适的参数能增大能隙；对于AB 堆叠，边缺陷占位能可对费米面周围近乎重合的4 条平带产生影响，从而打开一个能隙，而层间相互作用对平带部分影响不大，无法增大能隙宽度.引入边界线缺陷，对于2 种堆叠情况均会增强边态占据优势，打开边界量子通道，且改变占位能的符号可以调控电子分布在上下层的优势，增大占位能的数值会降低边态占据概率.缺陷格点的占位能可通过栅压调控，缺陷格点的层间跃迁可通过应力或衬底调控，这些都为制作新型双层石墨烯纳米器件提供了有力支撑.