Riesz 表现定理的向量值形式

汪成咏，王序岩

（北京交通大学数学系，北京 100044）

0 引 言

向量值函数积分，是普通（数值的）函数积分在向量值函数空间上的推广［1］.在分析数学的各个不同分支中［2］，由于核函数在不同领域的要求不同，所以需要引入向量值函数或向量值测度的积分［3］.在研究低维向量值函数空间上的有界线性算子的过程中，需要将广义泛函中的Riesz 表现定理推广到向量值函数空间［4］，这便是本文的研究意义.

本文先考虑C0与希尔伯特空间之间的有界线性算子的表现定理［5］，把闭区间上的连续函数空间上的有界线性泛函的Riesz 表现定理推广到局部紧的Hausdorff 空间上［6］，最终得到定义域是Hausdorff空间、值域是Banach 空间的向量值积分的Riesz 表现定理.

1 主体内容

如果σ是有界变差的可数可加H-值向量测度，则

其中

于是

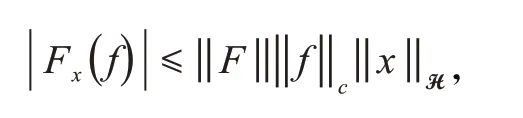
Fx是C0(Ω)上的有界线性泛函，

由Riesz 表现定理，存在Ω上唯一正则标量值的Borel 测度σx使得

且

于是与前一部分的讨论一样，存在Ω上可数可加的H 值向量测度σ，使得对于Ω的任意Borel 可测子集E，有

于是

依H 范数收敛.由此可表示为

故式( 3 )成立.

2 结束语

本文的主要内容包含3 个定理，分别用向量测度和空间同构的方式得到了从C0(Ω，H)到H、从C0(Ω，H)到C、从C0(Ω)到H的3 类有界线性算子的表现定理具体结构，把闭区间上的连续函数空间上的有界线性泛函的Riesz 表现定理推广到局部紧的Hausdorff 空间上，这个结论还是比较重要的.

作者在文［19］中通过引入H值缓增分布的方式，借助其Fourier 变换的特征得到了Banach 空间值的L2到L2空间上的有界线性算子的结构和范数的精确等式，但是在研究Banach 空间值的L1到L1空间上的有界线性算子的结构时，却发现之前的方式走不通，于是开始尝试从向量测度、算子测度以及全变差测度的角度来度量算子结构，在这个问题上将广义泛函上的Riesz 表现定理推广到向量值函数空间上就显得尤为重要了.