基于风电出力概率预测模型的源荷储日前概率优化调度

张紫菁，张 芳，姚文鹏

（天津大学智能电网教育部重点实验室，天津 300072）

0 引言

近年来随着国家对环境保护问题的重视，越来越多的风电机组实现了并网，风电逐渐成为我国第三大电源，然而风力资源本身所具有的波动性与随机性给电力系统安全运行带来了巨大的挑战。

为保证电力系统的安全稳定运行，在调度过程中需要考虑风电出力不确定性的影响，传统调度模式通常以预留一定备用容量的方式来应对风电出力的不确定性。文献［1］按照风电点预测出力的百分比为系统设置正负备用容量，但这种方式难以确定该百分比。文献［2-4］对系统各时段的备用容量大小进行动态设置，然而动态设置备用容量的方法仅能对系统内的总备用容量进行优化，难以实现各机组间备用容量的优化。有学者采用场景法［5］和鲁棒法［6-7］应对风电出力的不确定性。除上述方法外，文献［8］提出一种概率优化方法，单独考虑各时刻系统可能发生的扰动事件及其发生的概率进行优化调度，以应对系统中可能出现的机组故障或线路故障情况，目前尚未有研究将该方法应用于含风电的电力系统调度中。

在电力系统日前调度模型中，通常以风电点预测结果为依据，假设风电点预测误差服从某种特定的概率分布函数，文献［2-3］均采用该方法描述风电出力的不确定性，然而以特定的概率分布函数描述风电出力的不确定性对分布函数形式及其参数的选取具有一定的依赖性。非参数化的风电概率预测能够直接计算出预测误差分布的分布函数或分位点，不存在分布假设不合理的问题，但由于预测结果无法直接用解析式的形式表示，这对其应用造成了一定的困难，目前较少有研究将风电的非参数概率预测结果应用于电力系统日前调度中。

风电并网规模的增大增加了火电机组的调节压力，使储能设备和柔性负荷参与电力系统优化调度是提高系统灵活性、缓解火电机组调节压力的有效途径。文献［9］对用户负荷进行精细分类，并考虑蓄电池和电动汽车的充放电功能，构建智能小区内综合能源日前优化调度模型。文献［10］在优化过程中将储能设备的初始荷电状态SOC（State Of Charge）作为优化变量同时进行优化，并作为上一个调度时刻调整的依据。文献［11］将可中断负荷与储能设备作为灵活性资源，构建计及灵活性的随机优化调度模型。然而上述文献在构建储能设备的调度模型时，均只考虑储能设备最大充放电功率约束及最大、最小SOC 约束，忽略了运行过程中SOC 对储能设备充放电能力的影响。

在上述研究的基础上，本文将风电的非参数概率预测结果应用于电力系统日前调度中，摆脱了特定形式的概率分布函数对参数的依赖，更准确地描述了风电出力的不确定性。本文利用文献［8］中的概率优化调度方法解决风电出力的不确定性，构建含风电电力系统的源荷储日前概率优化调度模型，并根据SOC的变化动态调整储能设备充放电功率的上限值，改进了储能设备的数学模型。与现有调度模型相比，本文构建的日前调度模型具有以下优点：在考虑风电出力概率分布的前提下进行日前调度，避免了调度结果过于保守以及大量场景的生成与缩减过程；考虑风电出力偏离预测值后常规机组的调整情况，实现了备用容量在各机组间的最优分配；对储能调度模型的改进使储能设备的SOC维持在更安全的范围内，降低了储能设备发生过充或过放的风险。采用IEEE 6 节点系统进行算例分析，验证了所建模型的有效性。

1 风电出力概率预测

高精度的风电出力预测是一项提高含风电电力系统安全性的重要技术。点预测是目前最常用的风电出力预测形式，然而由于风资源本身具有随机性，且风电出力预测模型存在一定的固有缺陷，这使得风电出力点预测误差难以避免。风电出力的概率预测是利用气象数据、历史风电预测数据和实际数据，对未来时段风电出力的出力区间或概率密度函数PDF（Probability Density Function）进行预测。非参数概率预测方法不需要预先假设密度函数的表现形式，不存在分布假设不合理的问题，预测效果更好。目前，常用的非参数概率预测方法包括核密度估计法和分位数回归法，其中核密度估计法得到的预测值与观测值之间的匹配程度更高［4］，因此，本文采用该方法进行风电出力概率预测，具体过程如下。

1）获取待预测风电场的历史数据，包括风电出力日前点预测数据和实测数据，计算各时段的标准化出力点预测误差，计算公式为：

2）根据风电场的装机容量对风电出力日前点预测数据进行归一化处理，计算公式为：

3）根据各时段的归一化日前点预测出力对待预测风电场的历史数据进行区间划分。采用核密度估计法对每个区间子集的点预测误差PDF 进行估计，其估计量为：

式中：x为核函数的自变量。

4）对未来t时段的风电出力进行日前点预测，对日前点预测出力进行归一化处理，判断归一化日前点预测出力所处区间，并将步骤3）中对应区间的点预测误差PDF 估计结果作为未来t时段的点预测误差PDF。

2 储能侧及负荷侧调度模型

随着大量风电并网，部分常规电源被清洁能源所取代，这造成电力系统灵活性降低，仅依靠常规电源提供备用的传统调度模式难以有效应对净负荷的波动［11］，因此，本文考虑储能设备及可调度负荷参与电力系统日前调度，以提高电力系统的经济性与灵活性。

2.1 储能设备数学模型

储能设备在运行过程中需满足的约束主要包括最大充放电功率约束，最大、最小SOC约束以及调度周期内充放电功率平衡约束。在现有研究中，储能设备的最大充放电功率约束主要考虑储能并网逆变器容量的限制，忽略了储能设备运行状态的影响，但在实际运行中，储能设备的充放电能力受到其SOC的影响，当SOC 较大时，储能设备充电能力降低，此时应降低储能设备允许的最大充电功率限制，避免其SOC 迅速达到最大值，造成储能设备在日内调整阶段没有充电能力，同理，在SOC 较小时，应尽量降低储能设备允许的最大放电功率，使储能设备为日内调整阶段留有一定的放电空间，因此，本文改进储能设备的数学模型，其在运行过程中需满足的约束如下：

2.2 可调度负荷数学模型

本文主要考虑可转移和可中断2 类负荷参与电力系统日前调度，2 类负荷的价格激励方式参考文献［12-13］进行设置，具体模型如附录A 式（A1）—（A5）所示。

3 日前概率优化调度模型

在应对系统不确定性的方法方面，文献［8］提出一种概率优化方法，单独考虑各时段系统可能发生的扰动事件及其发生的概率进行优化调度，以应对系统内可能出现的机组或线路故障情况。本文将该方法应用于含风电电力系统的调度中，构建日前概率优化调度模型。

3.1 风电出力不确定性的处理

在含风电的电力系统中，系统的扰动事件主要为风电实际出力和负荷实际值偏离预测值的情况。现阶段，负荷预测的精确度远高于风电预测的精确度，因此，本文忽略负荷的不确定性，将风电实际出力偏离预测值视为系统的扰动事件。本文利用风电出力点预测误差PDF的分位点对点预测误差PDF进行分段，并将各段点预测误差的期望转换为风电实际出力的期望，从而建立风电出力的多状态模型，点预测误差PDF的分段数即为风电出力状态数。风电出力的多状态模型如附录B 图B1 所示，图中的分布函数为基于核密度估计法得到的t时段风电场w出力的点预测误差PDF。对于风电出力状态数为NK，w的多状态模型，其在各状态发生的概率及风电出力的期望分别为：

3.2 目标函数

由于储能设备的SOC与各时段的充放电功率密切相关，改变储能设备的充放电功率有可能影响后续时段的充放电能力，日前调度的主要目的是得到各时段储能设备的SOC 参考值，而可转移负荷需在整个调度时段内保持出力平衡，不能单独改变某时段的用电量，因此，在扰动事件发生后，本文不考虑利用储能设备和可转移负荷进行调整，储能设备和可转移负荷的运行状态与扰动事件发生前相同。综上，本文概率优化调度模型的目标函数F为：

3.3 约束条件

日前概率优化调度的约束条件主要包括扰动事件发生前系统的运行约束和扰动事件发生后系统的调整约束。扰动事件发生前系统的运行约束包括火电机组和风电机组的运行约束、系统需满足的功率平衡约束和线路容量约束以及储能设备、可中断负荷和可转移负荷的运行约束。扰动事件发生后系统的调整约束包括火电机组、风电机组和可中断负荷的调整约束以及系统应满足的功率平衡约束和线路容量约束。各约束条件参考文献［1，13］进行设置，具体约束条件如附录A式（A7）—（A20）所示。

4 算例分析

采用IEEE 6 节点系统进行算例分析，验证所建日前概率优化调度模型的有效性，该系统包含7 条线路和3 台火电机组。本文在节点2 接入装机容量为100 MW 的风电机组，在节点4 接入1 台储能设备，节点3—5 为负荷节点，负荷数据参考文献［15］，3个节点的负荷分配比例为1∶2∶2［3］，各负荷节点均包含1 个可中断负荷，节点5 还包含1 个可转移负荷。IEEE 6 节点系统结构如附录B 图B2 所示，火电机组、可转移负荷以及储能设备参数分别如附录B 表B1—B3 所示［12，16］。本文在MATLAB 2019b 平台上采用商业求解器Gurobi 9.1.0 对所建的日前概率优化调度模型进行求解。在无特殊说明的情况下，弃风惩罚项成本系数cW=150$／MW［17］，失负荷惩罚项成本系数cL=1 000$／MW，风电多状态模型的状态数为10，可中断负荷的单位容量成本=10$／MW，单位切负荷容量补偿费用=100$／MW［14］。

4.1 风电非参数概率预测方法验证

本文以比利时国家电网2019 年全年的风电日前点预测数据和实测数据为依据［18］，对风电的非参数概率预测方法进行验证。将归一化日前点预测出力离散为［0，0.2）、［0.2，0.4）、［0.4，0.6）、［0.6，0.8）、［0.8，1.0］5 个区间，以风电的日前点预测出力是否落入对应区间为样本分离条件，形成5 个样本子集，采用核密度估计法求取各子集点预测误差的PDF，如图1 所示（图中点预测误差为标幺值，后同）。以［0.2，0.4）区间的数据为例，分别采用非参数核密度估计模型与正态分布模型对其分布情况进行拟合，得到的结果如图2 所示。核密度估计法的最优窗宽由MATLAB 自带函数ksdensity 根据拇指原则自动选取。

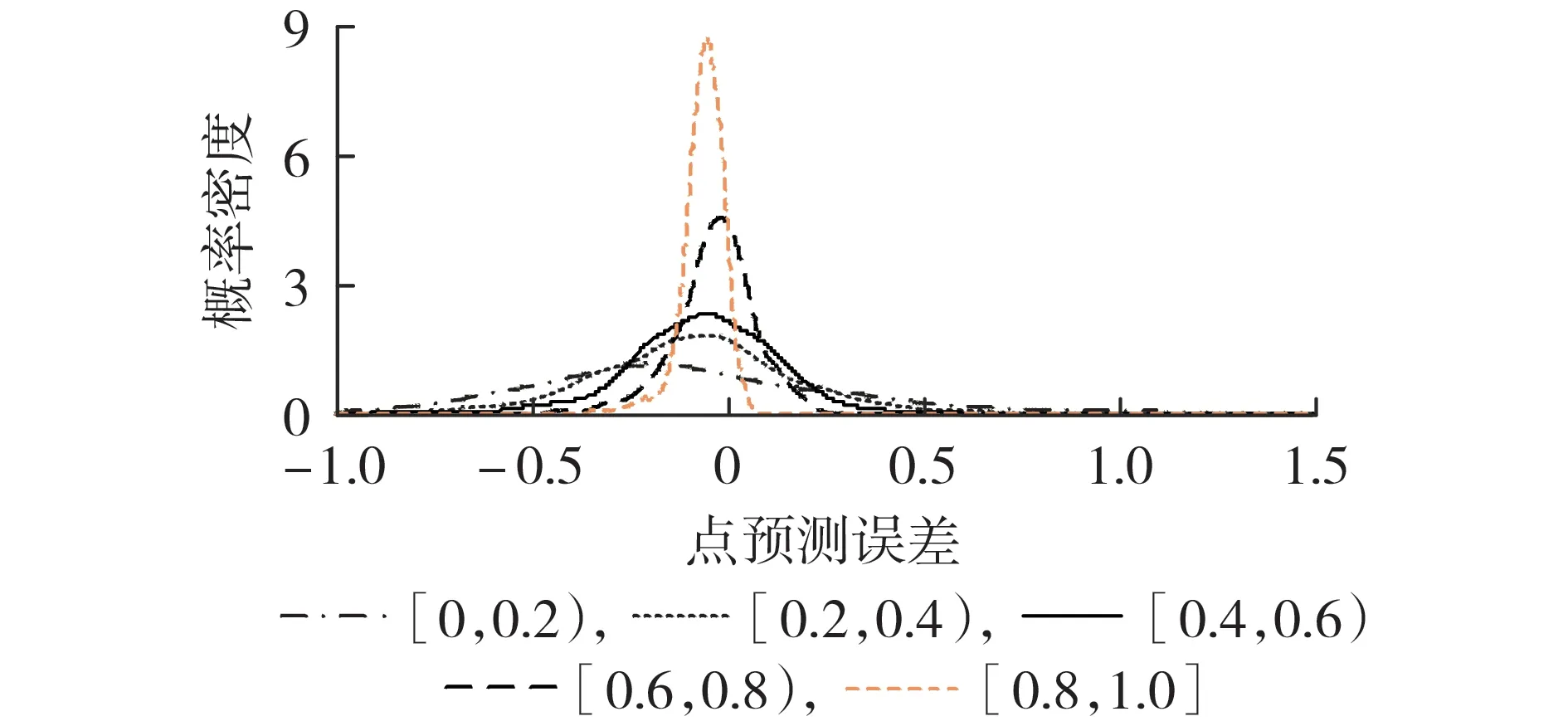
图1 不同区间内点预测误差的PDF预测结果Fig.1 PDF prediction results of point prediction error in different intervals

图2 不同模型下的点预测误差PDF拟合结果Fig.2 PDF fitting results of point prediction error for different models

由图1可见，不同日前点预测出力区间对应的点预测误差PDF存在明显差异。当日前点预测出力较小时，点预测误差的方差较大；当日前点预测出力较大时，点预测误差的方差较小。此外，不同点预测出力区间中产生的预测误差为负值的概率也不同，当日前点预测出力处于［0，0.2）、［0.2，0.4）、［0.8，1.0］区间内时，预测误差为负值的概率高于为正值的概率，当日前点预测出力处于［0.4，0.6）、［0.6，0.8）区间时，预测误差为负值的概率和为正值的概率近似相等。

由图2 可见，风电出力点预测误差的实际分布情况并不明显服从某种特定的概率分布形式，与采用正态分布模型拟合得到的PDF 相比，核密度估计模型因能够摆脱特定形式的概率分布函数对参数的依赖，拟合得到的概率分布结果能够更准确地描述风电出力预测误差的真实分布情况，进一步提高了预测模型的精确度。

4.2 日前概率优化调度模型有效性验证

本节仅考虑火电机组参与日前调度，为验证本文日前概率优化调度模型的有效性，将其与另外3种现有日前调度模型进行对比。通过对比利时国家电网2019 年风电历史数据的分析发现，其总体点预测误差近似服从标准差为0.26 的正态分布，因此各模型设置如下：模型1，确定性日前调度模型［19］，系统各时段的总备用容量设置为风电日前点预测出力的26%；模型2，确定性日前调度模型［19］，系统各时段的总备用容量设置为风电日前点预测出力的52%；模型3，文献［4］中的日前调度模型，利用风电非参数概率预测结果动态设置系统备用，系统各时段的总备用容量根据点预测误差累积概率分布函数的0.05 分位点和0.95 分位点进行设置；模型4，本文构建的日前概率优化调度模型。

采用比利时国家电网2020年1月的风电数据进行仿真，将各时段的风电数据均根据比利时电网风电场装机容量与IEEE 6 节点系统风电场装机容量的比值进行等比缩减。上述4 种模型在某天的备用容量优化情况以及在1 月的系统实际运行情况分别如图3 和表1 所示。图3 中，r（i=1，2，3）分别为火电机组i在t时段提供的正备用容量和负备用容量。

表1 各模型的系统实际运行情况Table 1 Actual system operation situation of different models

图3 各模型的机组备用容量优化结果Fig.3 Optimization results of unit reserve capacity for different models

模型1 和模型2 中均根据风电出力以固定比例设置系统的正负备用容量。由于模型1 中设置的备用容量较小，优化结果过于冒进，系统在实际运行时存在大量的弃风和失负荷现象，尽管系统的运行成本最低，但由弃风和失负荷引起的调整成本和风险成本之和过高，造成系统总成本最高。模型2 中为系统设置了较为充足的备用容量，其弃风量和失负荷量较模型1 明显减少，但在风电日前预测出力较小时，由于风电日前点预测误差较大，该模型仍不能为系统提供充足的备用容量，存在部分不必要的失负荷现象，而在风电日前预测出力较大时，由于风电日前点预测误差较小，该模型为系统提供了大量的备用容量，造成系统的运行成本和总成本过高。

模型3 和模型4 中均以风电出力的概率预测结果为依据进行优化调度，均能实现对系统备用的动态调节，使系统以最合理的机组组合方式运行，在降低系统运行成本的同时减少了系统的弃风量与失负荷量。但在动态调节系统的备用容量时，模型3 中仅能考虑各机组提供的备用总量满足系统备用需求的约束，而模型4 能够考虑各机组的调整成本，优化备用容量在各机组间的分配，使系统的调整成本更低。此外，在风电出力状态数为10 的情况下，与模型3 相比，模型4 中为系统设置了更大的备用容量，系统的弃风量与失负荷量进一步减少。

综上，模型4 的总成本、弃风量和失负荷量均为4 种模型中的最小值，证明了本文所建日前概率优化调度模型的有效性。

4.3 参数变化对日前调度结果的影响

在日前概率优化调度模型中，扰动事件数、弃风惩罚项成本系数及失负荷惩罚项成本系数均会对日前调度结果产生影响，本节分析这3个参数对1月日前调度结果的影响。

1）扰动事件数对日前调度结果的影响。

在本文的调度模型中，扰动事件数主要受到风电出力状态数的影响，风电出力状态数对日前调度结果的影响如图4所示。

由图4 可见，由于选取的弃风惩罚项成本系数及失负荷惩罚项成本系数较大，系统的运行状态主要受到风电多状态模型中端点状态（3.1 节中的第1个和第NK，w个状态）下的出力期望和的影响。随着风电出力状态数的增多，机组提供更大的正负备用容量以保证系统的安全运行，运行成本逐渐增加，系统的弃风量和失负荷量逐渐减少，此外，风电在端点状态下的出力期望和的变化量逐渐减小，系统弃风量和失负荷量减少的趋势以及运行成本增长的趋势均逐渐减缓。通过调整概率优化模型中的风电出力状态数，即扰动事件数，能够实现弃风量和失负荷量与系统运行成本之间的平衡。

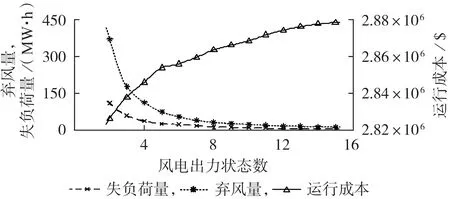
图4 风电出力状态数对日前调度结果的影响Fig.4 Influence of wind power output status number on results of day-ahead dispatching

2）弃风惩罚项成本系数对日前调度结果的影响。

弃风惩罚项成本系数cW对日前调度结果的影响如附录B 图B3 所示。cW的取值体现了系统对风能利用率的重视程度，其值越大表示系统对风能利用率的要求越高，系统需提供的负备用容量越大，运行成本越高，系统的弃风量越少。当cW增至30$／MW后，系统的运行成本和弃风量均不再变化，这意味着此时在优化过程中的各种风电出力状态下，机组均已提供充足的负备用容量以避免弃风现象的发生，但由于实际风电出力仍有极端状态出现，这导致此时的弃风量无法避免。需要说明的是，在本算例中，使系统运行成本和弃风量不再变化的弃风惩罚项成本系数临界值为30$／MW，该临界值受到风电出力状态数NK，w的影响。

3）失负荷惩罚项成本系数对日前调度结果的影响。

失负荷惩罚项成本系数cL对日前调度结果的影响如附录B图B4所示。cL的取值体现了系统对满足负荷需求的重视程度，其值越大表示系统对满足负荷需求的要求越高，因此，随着cL的增大，系统提供的正备用容量越大，运行成本逐渐增加，系统的失负荷量逐渐减少。当cL增至700$／MW 后，系统的运行成本和失负荷量均不再变化，这意味着此时在优化过程中的各种风电出力状态下，机组均已提供充足的正备用容量以避免失负荷现象的发生，但由于实际风电出力仍有极端状态的出现，这导致此时的失负荷量无法避免。

由上述分析可以看出，通过调整日前概率优化调度模型中的风电出力状态数、弃风惩罚项成本系数及失负荷惩罚项成本系数，能够实现弃风量和失负荷量与系统运行成本之间的平衡，进一步验证了本文模型的优越性。

4.4 储能调度模型验证

为验证本文改进的储能设备数学模型的有效性，设置2种调度模型进行对比：模型5，本文日前概率优化调度模型，仅考虑储能设备参与日前调度，储能设备采用传统模型［16］；模型6，本文日前概率优化调度模型，仅考虑储能设备参与日前调度，储能设备采用本文改进的模型。2 种模型中储能设备在某天的SOC情况如图5所示。

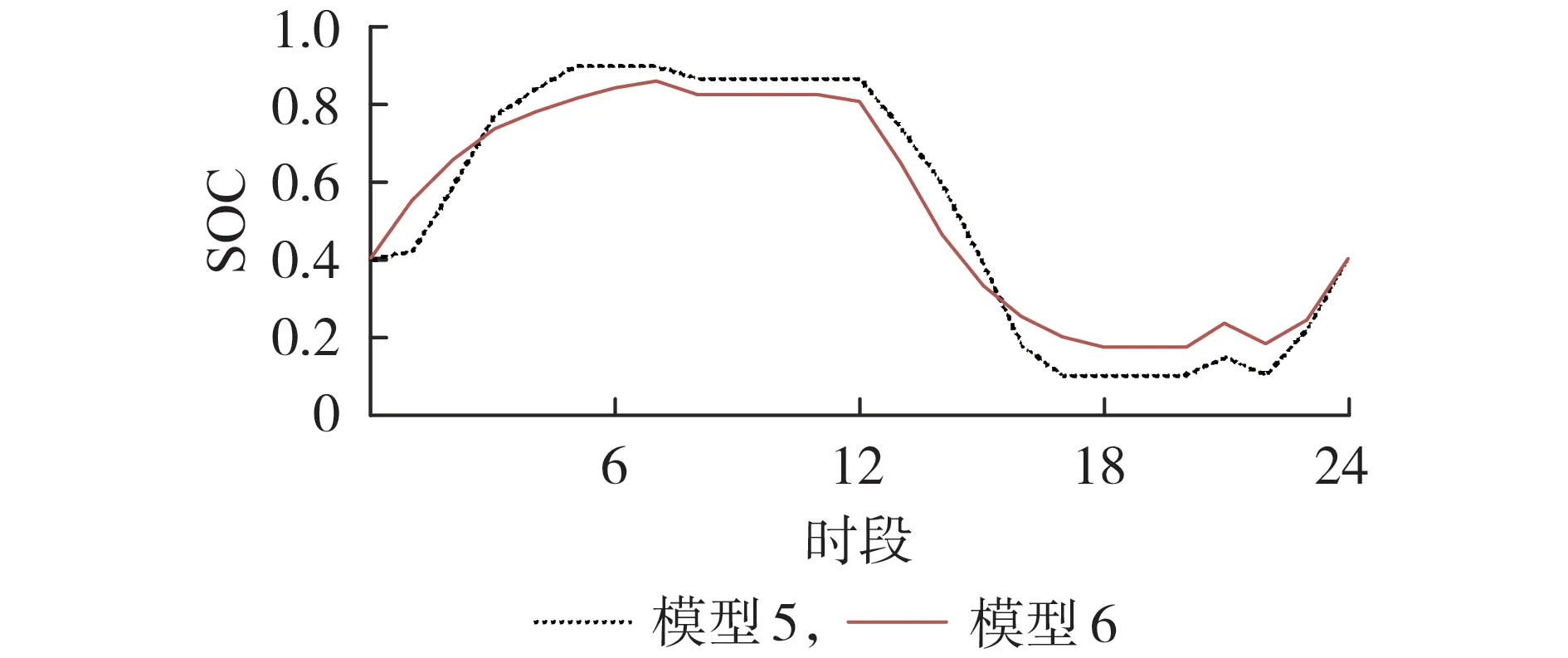
图5 储能设备的SOCFig.5 SOC of energy storage equipment

由图5可见：在时段5—7，模型5中储能设备的SOC 已达到上限值，在日内系统功率发生波动时，SOC 很容易超出上限值，造成储能设备过充，而尽管模型6 中储能设备的SOC 处于较高的水平，但始终维持在SOC 上限值以下，为日内系统功率发生波动时留有了一定的调整空间，降低了储能设备发生过充的风险；在时段17—19，模型5中储能设备的SOC已达到下限值，在日内系统功率发生波动时，SOC 很容易超出下限值，造成储能设备过放，而模型6 中的储能设备仍具有一定的放电空间，降低了日内系统发生波动时储能设备发生过放的风险。综上可见，本文改进的储能设备数学模型能够使储能设备的SOC 尽量处于较为安全的范围内，增大了储能设备的日内调整空间，降低了储能设备发生过充或过放的风险，更有利于储能设备的安全运行。

4.5 源荷储协调调度效果

为了验证储能设备与负荷侧调度对系统灵活性的影响，本节将各时段的负荷功率增大为原来的1.13倍，提高用电高峰时段的负荷量，增大负荷峰谷差，将模型4、模型6 及如下2 种调度模型进行对比：模型7，本文日前概率优化调度模型，仅考虑2 种可调度负荷参与日前调度；模型8，本文日前概率优化调度模型，考虑2 种可调度负荷与储能设备共同参与日前调度。

4 种模型在1 月实际运行时的总成本和失负荷量如附录B 表B4 所示。由表可知：模型4 中仅有火电机组参与日前调度，在用电高峰时段，若风电出力下降，则常规机组出力及爬坡能力的限制将造成系统灵活性不足，系统运行时的失负荷量较大；模型6中的储能设备能够在用电高峰时段放电，在用电低谷时段充电，实现了负荷转移，增强了系统灵活性，减少了系统运行时失负荷现象的发生；模型7 中的可转移负荷起到了与储能设备相同的作用，同时可中断负荷能够在用电高峰时段为系统提供一定的等效正备用容量，增强了系统灵活性，减少了系统运行时的失负荷量；模型8 中协同优化火电机组出力、负荷调度和储能设备出力，能够进一步增强系统灵活性，同时使系统经济性达到最优。

5 结论

本文考虑风电出力的不确定性，将风电的非参数概率预测结果应用于电力系统日前调度中，构建基于概率优化方法的电力系统源荷储日前概率优化调度模型，同时，考虑储能设备SOC对其运行状态的影响，改进储能设备的日前调度模型，最后采用IEEE 6 节点系统进行算例分析，验证了所建模型的有效性，所得结论如下。

1）将风电概率预测结果应用于电力系统日前调度模型中，能够更准确地描述风电出力的概率分布情况，且非参数概率预测方法能摆脱特定形式的概率分布函数对参数的依赖，进一步提高了预测模型的准确度。

2）对现有储能设备的充放电功率约束进行改进，根据SOC 的变化动态调整储能设备充电功率的上限值，能够在降低系统运行成本的同时，使储能设备的SOC 维持在更安全的范围内，增大了储能设备的日内调整空间，降低了储能设备发生过充或过放的风险，更有利于储能设备的安全运行。

3）基于概率优化方法构建的源荷储日前概率优化调度模型能够在考虑风电出力概率分布的同时避免大量场景的生成与缩减过程，动态优化系统备用容量，同时优化备用容量在各机组间的分配，降低机组在风电出力发生偏差后的调整成本。通过调整风电出力状态数、弃风惩罚项成本系数及失负荷惩罚项成本系数，能够实现弃风量和失负荷量与系统运行成本之间的平衡。

附录见本刊网络版（http：//www.epae.cn）。