基于电压灵敏度的配电网DG接纳能力不确定性分析

晋 飞，刘静利，刘晓亮，温国强，董逸超，王守相，赵倩宇

（1. 国网山东省电力公司潍坊供电公司，山东潍坊 261061；2. 天津大学智能电网教育部重点实验室，天津 300072）

0 引言

日趋严重的环境污染和能源危机不断促进世界各国对太阳能、风能等可再生能源的发展利用，我国在《新时代的中国能源发展》［1］中清晰描绘了2060年实现碳中和的“路线图”。在此背景下，受端电网接纳能力的精细化评估分析成为跨省区新能源消纳的核心问题［2］，而大规模分布式电源DG（Distributed Generation）接入配电网也将给间歇性DG 的高效接纳带来挑战。探究“双碳”目标下的新能源消纳场景与DG接纳能力已成为当前的研究热点之一［3］。

目前，国内外学者对配电网DG 接纳能力的分析方法开展了许多研究，数学分析方法主要包括解析法、智能优化方法和随机场景模拟法［4］。解析法和智能优化方法的结果偏于乐观而随机场景模拟法的计算时间过长，如何兼顾分析的准确性与快速性还有待进一步研究。电压灵敏度分析具有有效量化节点电压与注入功率解析关系的特点，为解决该问题提供了思路［5］，但随着配电网中间歇性源荷不确定性的影响愈加凸显，电压灵敏度确定性分析的适用场景将受到一定限制，因此，有必要研究电压灵敏度不确定性分析方法，这将有助于提升多元不确定环境下配电网DG 接纳能力分析的全面性、准确性和快速性。

常用的不确定性分析方法包括概率方法、鲁棒方法和区间方法等。概率方法的典型应用场景是概率机会约束规划：文献［6］以运行指标合格率为机会约束，建立光伏极限接入容量的概率机会约束规划模型，但模型中仅考虑光伏单点接入的情形，场景比较单一；文献［7］考虑风光互补特性，建立风光联合并网的DG 接纳能力概率机会约束规划模型；也有学者采用两阶段线性变换［8］和双层概率优化［9］的方式来提高计算效率。但概率方法的不足在于，不够精确的数据样本无法完全拟合DG 出力和负荷需求的概率密度函数PDF（Probability Density Function），这易使分析结果出现偏差。文献［10］将鲁棒方法引入DG 接纳能力分析中，该方法不依赖于随机变量的PDF，且计算保守性可通过参数调整灵活控制，因而该方法具有更好的求解性能；文献［11］建立DG接纳能力分析的两阶段鲁棒优化模型，可以有效量化多元不确定性影响，同时满足计算的鲁棒性和保守性要求；文献［12］在鲁棒模型的基础上考虑强对偶关系，利用条件风险价值重构方法将模型转换为双线性矩阵不等式问题，提高了计算精度。但鲁棒方法的保守性通常只针对DG 出力和负荷需求的不确定性，而难以量化配电网DG 配置方式潜在的不确定性，因此，由鲁棒方法得到的分析结果往往偏于乐观，与真实接纳能力之间存在一定偏差。相较而言，区间方法易获取不确定变量的上下界，具有模型简单、适用性强、求解快等优势。文献［13］以不确定条件下的能量损失最小为目标，建立网络重构区间优化模型，在量测配置不足时模型的优势更明显。但区间方法难以追踪不确定变量的相关性，通常具有计算偏于保守的缺点。仿射方法通过对多个变量的仿射多项式进行复杂的叠加运算，可以有效追踪多元不确定变量之间的相关性和耦合性［14］，避免“误差爆炸”现象的出现，从而降低计算保守性［15］。某种意义上而言，仿射方法是一种具有更高的计算精度、更快的计算速度和更好的收敛性的改进区间方法［16］，将其与DG 接纳能力分析相结合可有效提升分析计算的合理性与适应性。

综上，本文采用区间数学和仿射数学［17］量化多元不确定性因素与电压灵敏度间的映射关系，推导基于雅可比矩阵的仿射三相电压灵敏度方程，并结合随机场景模拟法［18-19］提出基于雅可比矩阵电压灵敏度的配电网DG 接纳能力不确定性分析方法，兼顾DG 接纳能力分析的准确性与快速性，同时为辅助配电网规划人员进行DG 接纳能力的在线快速分析和全面准确决策提供可能。

1 基于雅可比矩阵的仿射电压灵敏度方程

1.1 经典电压灵敏度方程

由经典雅可比矩阵J可得节点电压对节点有功／无功注入功率的灵敏度方程，如式（1）所示。

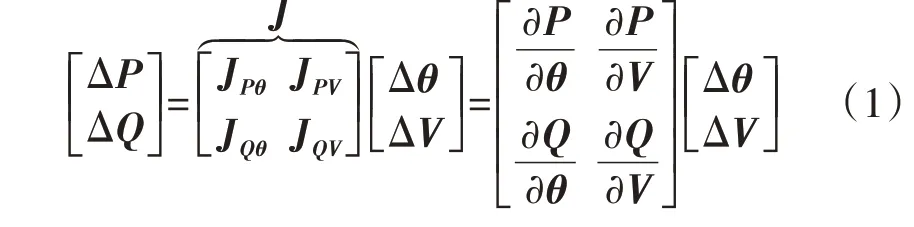
式中：JPθ和JQθ分别为节点电压相角对有功和无功注入功率的灵敏度；JPV和JQV分别为节点电压幅值对有功和无功注入功率的灵敏度；P和Q分别为节点有功和无功注入功率向量；ΔP和ΔQ分别为P和Q的变化量；θ和V分别为节点电压相角和幅值向量；Δθ和ΔV分别为θ和V的变化量。

当所有节点等效为PQ 节点时，JPθ和JQθ均为非奇异矩阵，因此，可将式（1）中的Δθ消去，得到ΔV对ΔP和ΔQ的灵敏度方程，如式（2）所示。

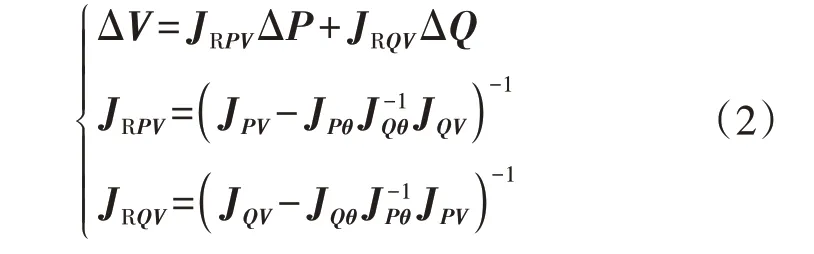
式中：JRPV和JRQV分别为n节点电力系统中ΔP和ΔQ对ΔV的n×n阶灵敏度系数矩阵，当网络拓扑不变时，其值均近似保持不变。

1.2 基于雅可比矩阵的仿射三相电压灵敏度方程

若考虑配电网的三相不平衡特性，同时忽略三相线路互阻抗，则可将式（1）改写为三相电压灵敏度方程，如式（3）所示。

因此，式（2）也可改写为：

进一步采用仿射数学量化节点注入功率的不确定性，可将式（4）所示的确定性三相电压灵敏度方程改写为仿射三相电压灵敏度方程，如式（5）—（7）所示。

进一步推导噪声项灵敏度方程，如式（9）所示。

由此构成仿射三相电压灵敏度方程，可追踪各节点电压幅值对节点注入功率不确定性变化的灵敏度。

2 计及DG 配置方式不确定性的过电压风险分析

本文在文献［20］的基础上考虑DG 配置方式不确定性引起的过电压严重程度，通过过电压场景分类和过电压严重程度修正系数来分析配电网的真实过电压风险IOR（Interval Overvoltage Risk）。

2.1 过电压DG配置场景分类

从而可形成以DG 安装容量PDG为横轴、以为纵轴的PDG-区间分布，包含Ⅰ类和Ⅱ类场景。Ⅰ类场景是必定发生过电压的DG 配置场景，不同时刻存在A 类（完全过电压）、B类（部分过电压）和C类（无过电压）这3 类情形，如图1 所示（图中系统最大电压幅值为标幺值，后同）；Ⅱ类场景是可能发生过电压的DG配置场景，存在B类、C类这2类情形。

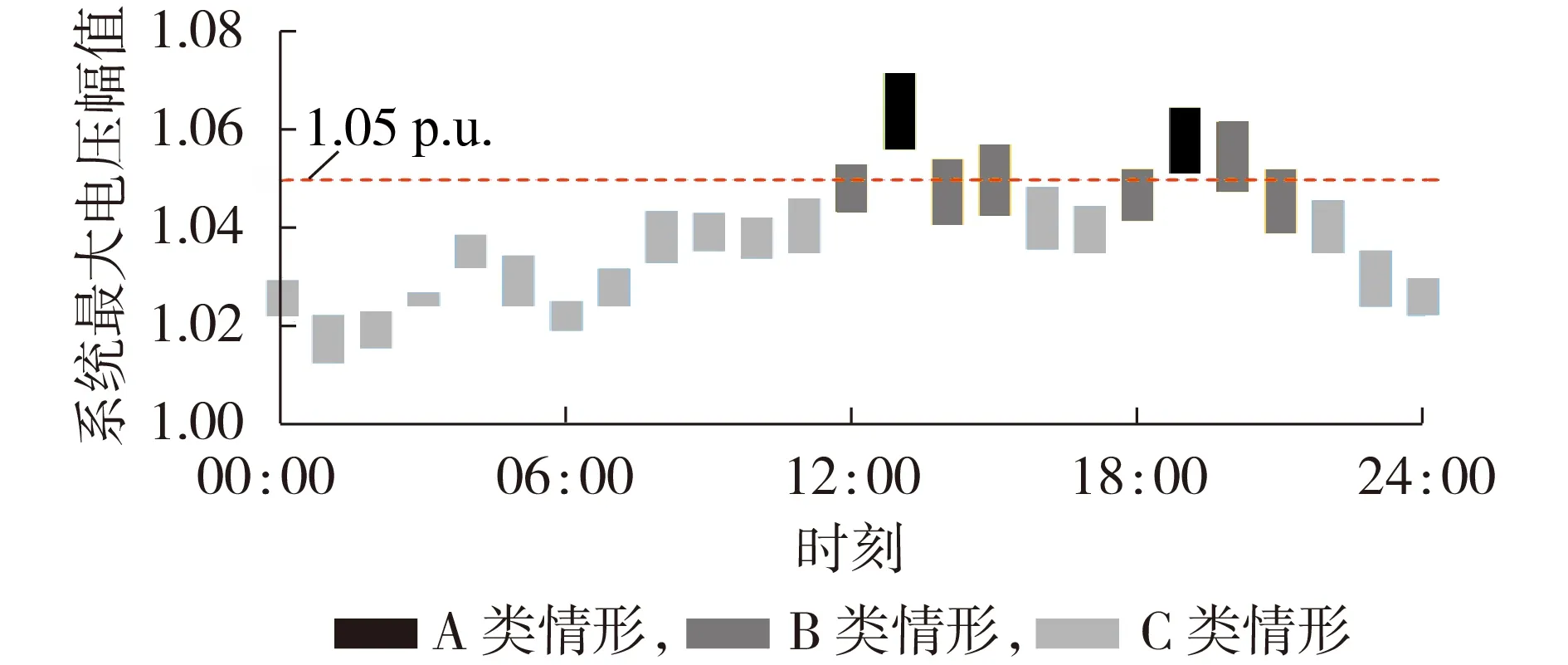
图1 Ⅰ类场景不同时刻3类情形示意图Fig.1 Schematic diagram of three situations at different moments for Scenario Ⅰ

2.2 过电压严重程度修正系数的计算

Ⅰ类和Ⅱ类场景的过电压严重程度不同，需要对这2 类场景的过电压严重程度修正系数进行差异化计算。

1）Ⅰ类场景过电压严重程度修正系数。

若将Ⅰ类场景各时刻的最大仿射电压表示为式（13），则过电压严重程度可由A 类和B 类情形的最大仿射电压幅值的过电压幅度来衡量，如式（14）—（18）所示。在此基础上，Ⅰ类场景过电压严重程度修正系数δⅠm可根据Ⅰ类场景平均过电压幅度进行计算，如式（19）、（20）所示。

2）Ⅱ类场景过电压严重程度修正系数。

若Ⅱ类场景各时刻的最大仿射电压表示为式（21），则过电压严重程度可由B 类情形的最大仿射电压幅值的过电压幅度来衡量，如式（22）、（23）所示。在此基础上，Ⅱ类场景过电压严重程度修正系数δⅡm可根据Ⅱ类场景平均过电压幅度进行计算，如式（24）所示。

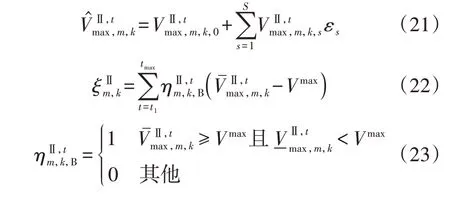
2.3 IOR计算与DG接纳能力分析

3 基于电压灵敏度的DG 接纳能力不确定性分析方法

4 算例分析

采用附录A图A1所示的IEEE 33节点配电网进行仿真，系统基准电压和基准容量分别为12.66 kV和10 MV·A，平衡节点电压幅值为1.00 p.u.，总负荷为3 715+j2 300 kV·A。为简化分析，所有DG 和负荷均采用附录A 图A2所示的区间变化特性，功率因数分别为1和0.9。

由初始时刻t0的1 次潮流计算得到电压灵敏度系数矩阵和，将蒙特卡罗仿真次数设为6 000，即构造1.98×105个DG 配置场景。根据式（8）和式（10）快速计算各场景的仿射电压幅值变化量进而形成PDG-区间分布，如图2 所示。图中，Z点表示在系统最大电压幅值超过1.05 p.u.的所有场景中对应的最小DG安装容量为2600 kW。

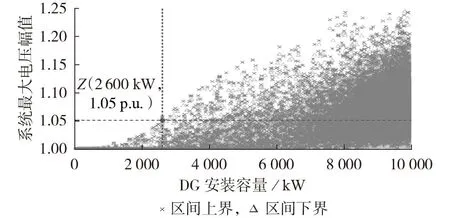
图2 PDG-区间分布图Fig.2 Plot of PDG- interval distribution

若将DGCI 宽度设为100 kW，将mmax设为100，将最大电压幅值上限Vmax设为1.05 p.u.，则可得到各DGCI 中的Ⅰ类和Ⅱ类场景总数和。进一步计算Ⅰ类和Ⅱ类场景的过电压严重程度修正系数δⅠm和δⅡm，当电压变化比例系数CΔV设为5.0 时，各DGCI的IOR区间值变化情况如图3所示。

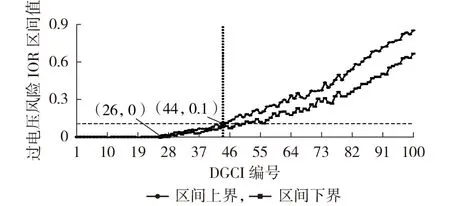
图3 IOR区间值随DGCI的变化情况Fig.3 Variation condition of IOR interval value along with DGCI

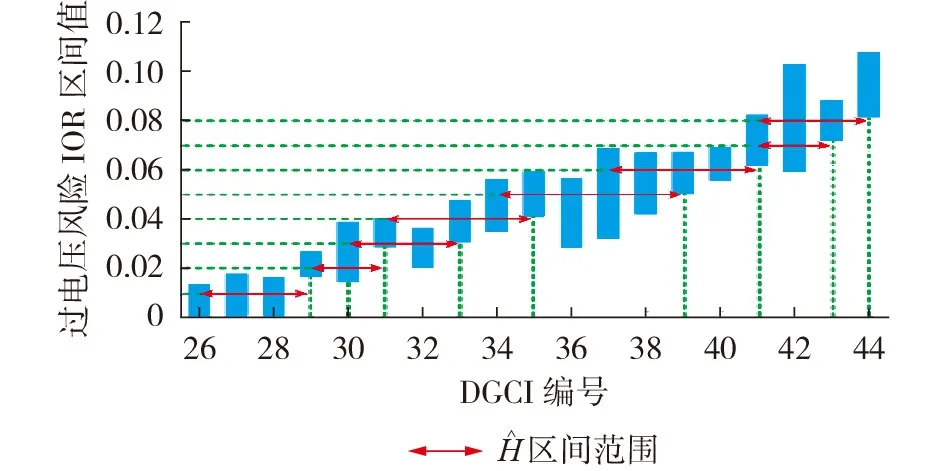
图4 DGCI编号在［26，44］之间时IOR区间值的变化情况Fig.4 Variation condition of IOR interval value when DGCI number is within［26，44］

在此基础上，可得到基于电压灵敏度的配电网DG接纳能力区间值计算结果，如表1所示。

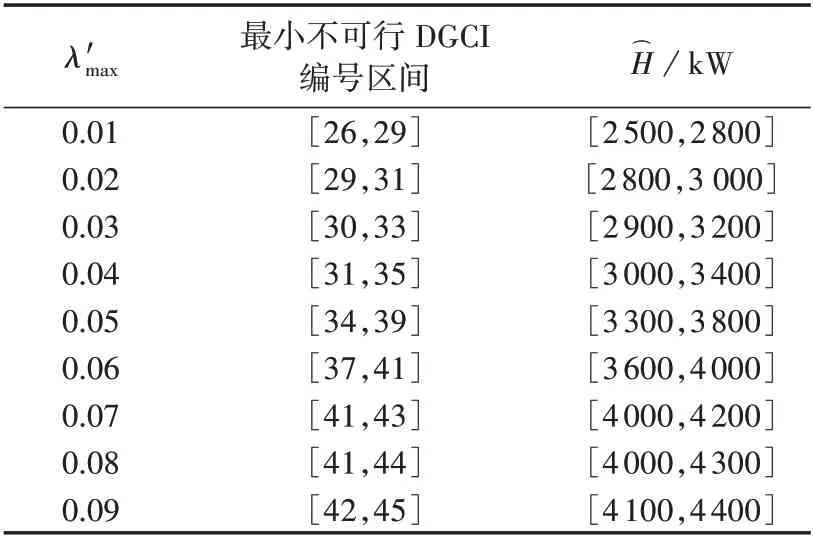
表1 DG接纳能力区间值计算结果Table 1 Calculative results of DG hosting capacity interval value

为验证电压灵敏度方法兼顾DG 接纳能力分析的准确性与快速性的效果，进一步将基于复仿射潮流的DG 接纳能力分析方法（记为方法Ⅰ）与基于电压灵敏度方法的DG 接纳能力分析方法（记为方法Ⅱ）进行对比。对于IEEE 33 节点配电网和湖北55节点配电网，当仿真参数相同时，2 种分析方法的DG 接纳能力区间值计算结果和计算时间对比分别如图5和表2所示。

表2 2种分析方法的计算时间对比Table 2 Calculation time comparison between two analysis methods

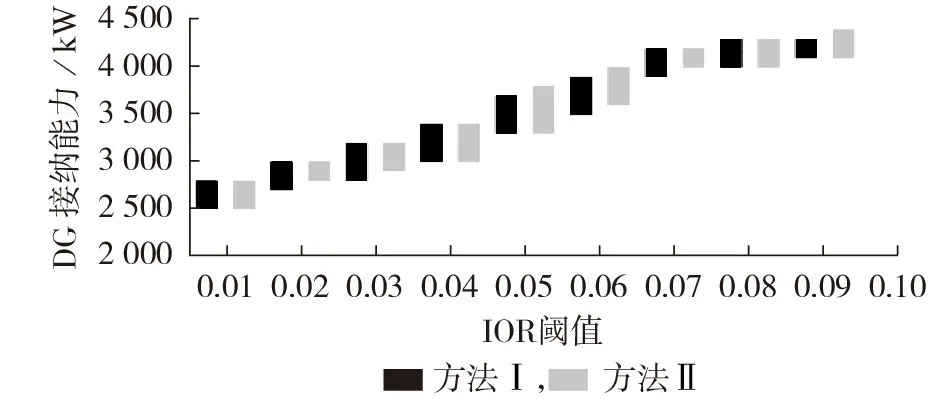
图5 2种分析方法的计算结果对比Fig.5 Result comparison between two analysis methods

由图5 和表2 可见：2 种分析方法计算得到的DG 接纳能力区间值H︵整体上较接近；对于IEEE 33节点配电网，当DG 配置场景总数为1.98×105时，方法Ⅱ相比方法Ⅰ计算时间缩短36.44%；对于湖北55节点配电网，当DG 配置场景总数为3.30×105时，方法Ⅱ相比方法Ⅰ计算时间缩短36.19%。由此验证了所提电压灵敏度方法兼顾DG 接纳能力分析的准确性与快速性的效果。

5 结论

本文基于区间数学和仿射数学进行配电网DG接纳能力的不确定性分析，主要结论如下：

1）采用区间数学和仿射数学量化多元不确定性因素与电压灵敏度间的映射关系，推导基于雅可比矩阵的仿射三相电压灵敏度方程，有效追踪节点电压幅值对节点注入功率不确定性变化的灵敏度；

2）提出基于雅可比矩阵电压灵敏度的配电网DG接纳能力不确定性分析方法，与基于复仿射潮流的DG 接纳能力分析方法相比，所提方法的计算精度能够得到保证，同时在IEEE 33 节点配电网和湖北55 节点配电网中，所提方法的仿真计算时间可分别缩短36.44%和36.19%，由此验证了所提方法兼顾DG接纳能力分析的准确性与快速性的效果。

附录见本刊网络版（http：//www.epae.cn）。