基于自适应学习率萤火虫算法的多能源系统联合优化调度

张荣权，李刚强，卜思齐，刘芳，朱玉祥

（1.南昌交通学院交通运输学院，南昌 330100；2.河南省智能机器人行为优化控制国际联合实验室（黄淮学院），河南驻马店 463000；3.香港理工大学电机工程学系，香港 999077）

0 引言

随着人们对环境气候变化影响的日益关注，许多国家根据经济发展情况制定了相应的减碳目标。为了促进减碳目标的实现，新能源发电在全球范围迅速发展，渗透率逐渐提高并在电力系统中发挥了重要作用［1］。可再生新能源（如风能、太阳能）具有间歇性、随机性的特点，规模化的新能源发电并网运行会对能源利用效率、新能源消纳、多能源管理、电网稳定运行等产生不利影响。为解决以上问题，多能源系统（Multi-energy System，MES）近年来得到了广泛关注，对于推动可再生能源和分布式储能的发展有着重要意义［2］。MES是指利用先进的技术整合一定区域内的风能、光伏、天然气、电能、热能、冷能等多种资源，满足系统内多元化用能需求，同时可借助主电网的双向通信能力与其他发售电商进行电力交易的系统［3］。由于MES包括生产、转换、存储、消费等复杂环节，其经济运行优化必然面临诸多挑战［4］。

针对MES 的运行优化已有许多文献进行了研究，文献［5］采用了2 种电池储能系统（Battery Energy Storages System，BESS）的经营战略对MES 的运行成本进行优化：第1种战略是平衡电力负荷；第2 种战略是在平衡MES 电力负荷的基础上盈利，但此模型并未考虑新能源发电。文献［6］提出了含风光储的MES 优化模型，以最小化MES 的运行成本、主电网的网损和节点电压偏差为目标。结果显示，风光储协调运行方式可以有效减少MES 的运行成本，但所提模型对BESS 的充放电特性及运行成本缺乏考虑。文献［7］构建了风-光-荷不确定性的数据驱动型机组组合模型，但未考虑BESS 的放电损耗成本以及碳排放惩罚成本。文献［8］采用粒子群优化算法对含可再生能源发电的储能模型进行多目标优化求解。文献［9］采用萤火虫算法对冷热电联供（Combined Cooling，Heating and Power，CCHP）系统的多目标优化调度模型进行求解。但粒子群优化算法和萤火虫优化算法存在收敛速度较慢且容易陷入局部最优解等问题［6］。

针对多能源系统的联合运行优化，本文构建了以新能源发电站、BESS 以及CCHP 装置作为承载对象的新型MES 模型。为降低购电成本和系统的碳排放惩罚成本、减少“弃风弃光”、实现价差套利以及保障能源综合利用，分别将新能源发电站、BESS和CCHP接入MES。在此基础上构建MES的经济优化模型，以弃风弃光惩罚成本、BESS放电损耗成本、主电网购售电成本、燃气轮机燃气成本、碳排放惩罚成本等为目标函数，以光伏与风力发电机组的出力特性、BESS 的充放电特性、冷热电平衡等为约束条件对模型进行求解。针对经典萤火虫算法/粒子群优化算法在求解整个MES 的过程中存在收敛速度慢、不能寻找最优解问题，提出了一种自适应学习率萤火虫算法（Adaptive Learning Rate Firefly Algorithm，ALRFA），通过引入自适应学习速率参数，可避免萤火虫算法陷入局部最优、收敛速度慢的问题。试验通过对比经典粒子群优化算法（Particle Swarm Optimization，PSO）［10］、经典萤火虫算法（Firefly Algorithm，FA）［11］、文化基因萤火虫算法（Memetic Firefly Algorithm，MFA）［12］来验证ALRFA的寻优解能力，以某园区夏天某一天的冷热电负荷为例，验证所提模型与优化算法的有效性和可行性。

1 MES优化模型

1.1 MES结构

MES 由新能源发电站、BESS 和CCHP 组成，如图1所示。新能源发电站包括风力发电机组和光伏发电机组，BESS主要是对系统内电能进行充放和储存，CCHP 包括燃气轮机、辅助锅炉、热回收系统、制冷/热设备［13］。在这3 个子系统中，用户的电负荷由新能源发电机组、BESS、燃气轮机以及主电网共同供给。当新能源发电机组、BESS以及燃气轮机不能保证用户的电负荷需求时，则由主电网作为备用电源为用户供电。反之，若新能源发电机组、BESS 以及燃气轮机足够保证用户的电负荷需求，则系统的剩余电量将售卖到主电网［6］，这使得MES 可孤岛运行也可并网运行。用户的冷负荷由电制冷器和吸收式制冷器共同供给；用户的热负荷由加热线圈供给。

图1 多能源系统结构Fig.1 Schematic structure of an MES

1.2 新能源发电站

1.2.1 风力发电机组

风力发电机组的运行成本主要包括设备维护成本、人工成本和弃风惩罚成本［14］。风力发电机组建成后，设备维护成本和人工成本可分摊在风力发电度电成本C11上［15］。

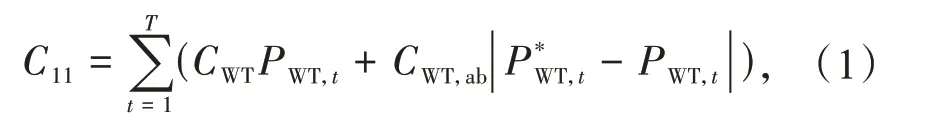
式中：T为次日24 h 的优化调度时间；CWT为风力发电机组的单位发电成本；CWT，ab为风力发电机组的单位弃风惩罚成本；PWT，t为风力发电机组t时刻实际被调用的风电功率；为风力发电机组t时刻的发电功率。

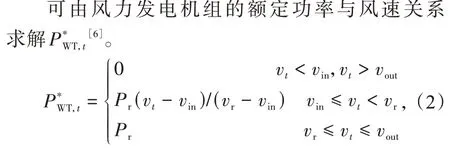
式中：vt，vin，vout，vr，Pr分别为t时刻的实际风速、切入风速、切出风速、额定风速以及风力发电机组的额定功率。

1.2.2 光伏发电机组

光伏发电机组的运行成本主要包括设备维护成本、人工成本以及弃光惩罚成本。类似风力发电机组，设备维护成本和人工成本可分摊到光伏发电度电成本C12上。

式中：SPV，ηPV，It分别为光伏板的面积、光照转化效率以及t时刻的光照强度。

1.3 BESS

BESS 在电价较低时存储MES 的剩余电负荷或购买主电网的电负荷，而在电价高涨时供给MES 的用户或销售给主电网，从而降低了MES 的运行成本。虽然BESS 有助于减小系统的运行成本［16］，但BESS 的运行成本受诸多因素影响，如放电行为（放电损耗成本）、峰值电流、温度、设备维护成本、人工成本等［17］。考虑到放电行为对电池寿命有明显影响，因此需要额外考虑放电损耗成本［18］。其他温度、峰值电流、设备维护成本等影响可折算到充放电成本C2上。

式中：α，β，γ分别为1-SOC，t的二次项系数、一次项系数和常数项系数；SOC，t为t时刻BESS 的SOC；EB为BESS的容量；EB，t为t时刻BESS存储的电量。

从式（5）—（7）可以看出，放电过程中，BESS 的放电功率越大或SOC越小，放电损耗成本越高。

在MES 的优化运行中，BESS 应满足以下约束条件。

（1）假设t时刻BESS 的充电状态为SOC，t，则t+1时刻的SOC为

式中：ηch，ηdis分别为BESS的充、放电效率。

（2）为了保证BESS 处于良好的工作状态，充放电过程中BESS的SOC受到容量限制。

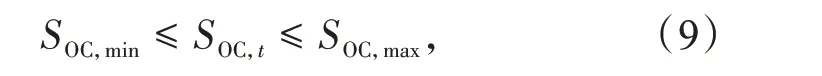
式中：SOC，min，SOC，max分别为BESS的SOC上、下限。

（3）BESS 的充放电功率受最大、最小充放功率限制。

1.4 CCHP装置

MES 的CCHP 主要包括燃气轮机、热回收系统、辅助锅炉、吸收式制冷器、加热线圈等设备。CCHP先通过燃气轮机进行发电，发电剩余热量部分通过热回收系统为用户提供冷热负荷，不足供冷热部分由辅助锅炉补给［20］。

CCHP 的运行成本主要包括燃气轮机燃气成本、辅助锅炉燃气成本、碳排放惩罚成本、从主电网的购电成本、向主电网的售电成本、设备维护成本及人工成本等［13］。设备维护成本、人工成本和其他成本可折算到燃气成本C3。

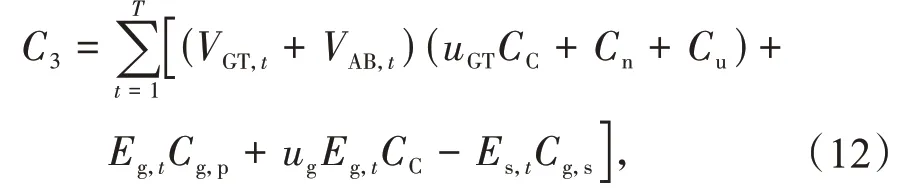
式中：VAB，t，Eg，t，VGT，t，Es，t分别为t时刻辅助锅炉的燃气量、从主电网的购电量、燃气轮机的燃气量及向主电网的售电量；ug，uGT，Cg，p，Cg，s，Cn，CC，Cu分别为从主电网购电的碳排放转化因子、燃气轮机/辅助锅炉的碳排放转化因子、从主电网的购电价格、向主电网的售电价格、天然气价格、碳排放价格及单位折算成本。

燃气轮机的发电/供热量EGT，t主要取决于燃气轮机的燃气消耗量和燃气轮机发电/供热的转化效率。

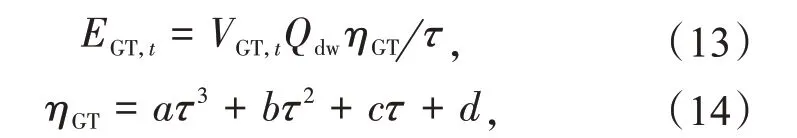
式中：Qdw，ηGT，τ分别为燃气低位热值、燃气轮机发电/供热的转化效率和负载因子；a，b，c，d为常数。

MES 优化运行中，CCHP 包括冷热电平衡约束条件。

（1）电能平衡约束：MES 的电能分别来自从主电网的购电量，风力发电机组、光伏发电机组的发电量，燃气轮机的发电量以及BESS 的放电量；它们的和等于电制冷器的消耗量、用户的电负荷、向主电网的售电量以及BESS的充电量。

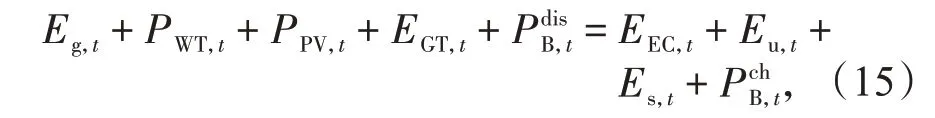
式中：Eu，t，EEC，t分别为t时刻用户的电负荷及t时刻电制冷器的消耗量。

电制冷器的消耗量由电制冷器的冷负荷决定。

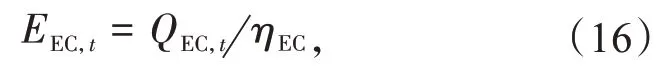
式中：QEC，t及ηEC分别为t时刻电制冷器的冷负荷及电制冷器的转化效率。

（2）热平衡约束：用户的热负荷来自加热线圈

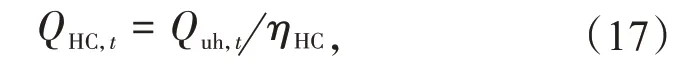
式中：Quh，t，ηHC及QHC，t分别为t时刻用户的热负荷、加热线圈的转化效率及t时刻加热线圈的消耗量。

（3）冷平衡约束：用户的冷负荷来自电制冷器的冷负荷以及吸收式制冷器的冷负荷

式中：Quc，t为t时刻用户的冷负荷；QAC，t为t时刻吸收式制冷器的冷负荷。

吸收式制冷器的消耗量来自辅助锅炉和热回收系统。

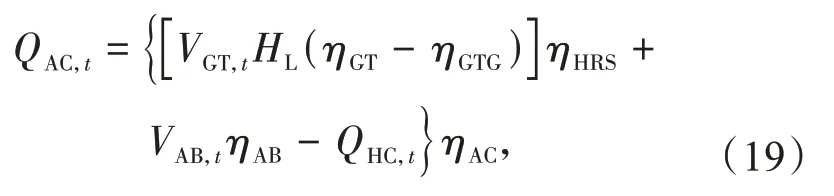
式中：ηGTG，ηHRS，ηAB，ηAC分别为燃气轮机发电的转化效率、热回收系统的转化效率、辅助锅炉的转化效率和吸收式制冷器的转化效率。

CCHP设备的容量约束可参考文献［13］。

1.5 MES的经济优化模型构建

基于以上分析，MES 的运行成本C包括风力发电机组的运行成本、光伏发电机组的运行成本、BESS 的运行成本和BESS 的运行成本；约束条件主要包括光伏与风力发电机组的出力特性、BESS的充放电特性和冷热电平衡。

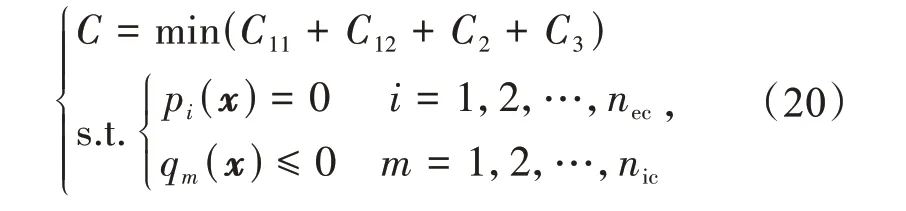
式中：x为决策向量；pi(x)为第i个不等式约束；qm(x)为第m个不等式约束；nec及nic分别为等式约束和不等式约束的个数。等式约束和不等式约束分别对应1.2—1.4节的等式约束和不等式约束。

2 求解算法

考虑到经典萤火虫算法的收敛速度慢、不能寻找到最优解，本文提出了一种ALRFA，以提高寻优速度。

2.1 FA

FA是一种新型启发式优化算法，灵感来自于萤火虫闪烁的行为。每只萤火虫闪烁行为作为一个信号系统，以吸引其他的萤火虫［11］。FA 假设以下4种理想情况：（1）所有的萤火虫不分性别，这就意味着所有的萤火虫都能吸引对方；（2）假如有一只萤火虫的亮度比另一只萤火虫的亮度更大，则亮度更小的会被亮度更大的吸引，此外，随着萤火虫之间距离的增大，吸引强度将呈指数下降［11］；（3）每只萤火虫的亮度可以对应一个目标函数优化值；（4）如果没有比一个给定的萤火虫更亮的萤火虫，它会随机移动。因此，任何2 只萤火虫（xi与xj）在第k+1 次迭代时的移动公式为

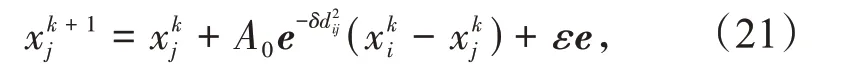
式中：dij为xi和xj之间的距离；δ为吸引系数；A0为dij等于0 时的吸引力；ε为步长因子，在FA 中ε通常设置为0～2；e为一个服从高斯分布的矢量。

2.2 ALRFA

通过式（21）可以看出，FA的搜寻行为是根据萤火虫的亮度以及一个服从高斯分布的矢量进行移动，该算法存在以下缺点：（1）亮度较小的萤火虫受较多亮度较大的萤火虫吸引，而数量巨大的萤火虫吸引不仅导致萤火虫算法的移动速度变慢，还使得可行解在解空间振荡［21］；（2）MES 的优化模型存在高维度以及非线性特性，当萤火虫移动到全局解附近时，萤火虫之间的距离dij逐渐缩小，萤火虫之间的吸引力逐渐增大，将会使萤火虫的移动距离过大而陷入局部解。为了克服以上缺点，本文基于均方根传递（Root Mean Square Prop，RMSProp）算法的思路和灵感［22］，提出了一种ALRFA，通过引入学习速率参数控制收敛速度，然后对移动记忆进行一次指数平滑，以实现自适应控制学习速率参数，使得收敛更加迅速和稳定。请注意，此处提出的ALRFA与自适应步长算法完全不同［23］，尽管它们名字看起来相似。自适应步长算法通过引入荧光因子自适应调整步长，然而本文所提算法先通过引入学习速率参数，再对记忆的一次指数平滑实现自适应学习率。ALRFA的移动可以描述为

从式（23）—（24）可以看出：搜索过程中，dk+1i剧增时W k+1i也增大，相当于减小了学习率，从而通过抑制振荡方式加快收敛速度；反之，dk+1i剧降时W k+1i也降低，相当于增大了学习率，从而通过跳出局部收敛方式提高收敛精度。

3 仿真及结果分析

3.1 参数设定

MES 的运行参数包括风力发电机组、光伏发电机组、BESS 及CCHP。其中：风力发电机组的额定风速以及其他参数（切入风速和切出风速）可参考文献［24］；光伏发电机组的光伏板面积与光照转化效率可参考文献［25］；光照强度及风速按数据驱动方法进行估算［26］（假设预测不存在误差）。BESS 参数ηch，ηdis，SOC，min，SOC，max，，，，分别设置为0.95，0.98，0.10，0.98，0 kW，100 kW，0 kW，100 kW。CCHP 的燃气轮机和电制冷器有功容量分别设置为2 000，1 500 kW；CCHP 转化效率ηEC，ηHC，ηAB，ηAC，ηGTG，ηGT，ηHRS分别设置为1.20，0.80，0.80，0.70，0.29，0.90，0.80，0.13。风力发电机组成本CWT和CWT，ab分别设置为0.200，0.035 元/（kW·h）；光伏发电机组成本CPV和CPV，ab分别设置为0.150，0.035 元/（kW·h）；BESS 成本系数α，β，γ，r，CB分别设置为0.002 0，0.006 0，0.008 5，0.200 0，0.035 0元/（kW·h）；CCHP 的转换因子及成本系数ug，uGT，Cn，CC，Cu分别设置为968 g/（kW·h），220 g/（kW·h），1.6 元/m3，0.000 02 元/（kW·h）和0.3 元/m3。向主电网的售电价格Cg，s可以通过数据驱动方法获得［27-29］。为简化计算，本文引入电力现货市场某一天的节点边际价格进行模型计算。值得注意的是，由于用户的购电价格包含输配电价和政府性基金与附加（本文假设0.15 元/（kW·h）），因此向主电网的购电价格Cg，p需要在向主电网的售电价格的基础上加上输配电价和政府性基金与附加。试验以某园区夏天某一天的冷（Quc，t）、热（Quh，t）以及电（Eu，t）负荷数据为例，验证所提出系统和算法的有效性和可行性。其中，用户向主电网的分时售电价格如图2所示，用户的冷、热、电负荷如图3所示。

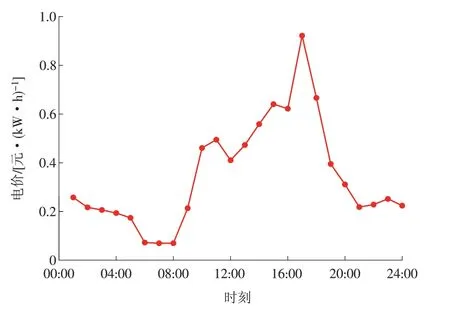
图2 用户向主电网的分时售电价格Fig.2 Time-of-use tariffs from customer side to power grid

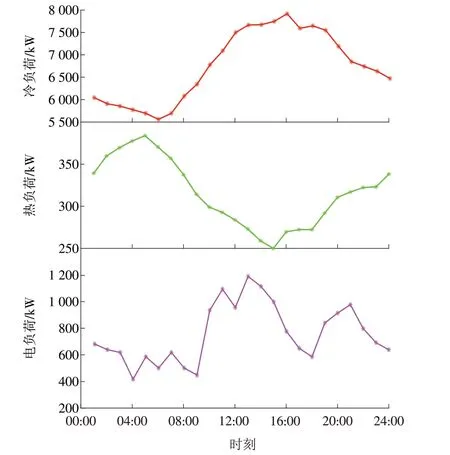
图3 用户一天的冷热电分时负荷Fig.3 Time-of-use tariffs for cooling，heating and electricity loads on a representative day

文中ALRFA 的参数（wk，μ0，NG，np，其中：np为萤火虫的数目；NG为ALRFA 的迭代次数）对于所提优化模型求解至关重要。权重系数wk决定了移动记忆储存的大小：若wk很小，则更久远的移动记忆对当前移动几乎没有影响；若wk很大，则更久远的移动记忆对当前移动存在较大影响。为了保障快速收敛，仿真发现wk为0.80～0.95 时收敛速度相近。10 次迭代后wk设置为0.90，其意义是只计算近10次的移动记忆一次指数平滑值（为了简化，在10 次迭代前wk设置为0）。若初始学习率μ0很小，将会影响算法的收敛速度；若μ0很大，将会提前进入局部收敛。仿真显示，μ0为250～800 时算法趋于收敛，本文设置μ0为500。若萤火虫数目np小于10，相当于萤火虫吸引数目过少，则收敛速度将变慢；若np大于100，表明萤火虫吸引数目过多，则收敛速度将缓慢。经过多次搜索验证，本文设置np为30。若ALRFA 的迭代次数NG很小，将不能保障优化算法的收敛性，仿真发现NG为900～1 000 时算法渐近稳定，本文设置NG为1 000。其他参数ε，A0，δ，ξ分别设置为2.0，1.0，1.0，0.5。

3.2 求解算法分析

以优化MES 的运行成本为目标，选择经典PSO，FA，MFA 算法来验证所提ALRFA 的性能。各算法的收敛性如图4 所示，本文所提ALRFA 算法在迭代500 次后的收敛误差最小，PSO，FA 和MFA 均存在较大误差。这是因为ALRFA 的移动距离如果减小，学习率将增大，会使得收敛时通过跳出局部解的方式提高收敛精度。此外，ALRFA 具有较快的收敛速度，在迭代次数为10～100 时（图4 中椭圆形虚线），ALRFA 的收敛速度和曲线光滑度明显优越于FA，主要原因是10 次迭代后萤火虫的移动记忆被一次指数平滑，相当于对过去10个数做了指数加权。ALRFA 的移动距离如果增大，学习率将减小，使得收敛过程中减小了一些振荡，从而加快了收敛速度。可以看出，对MES 的优化模型进行求解时，相比于其他算法，ALRFA 的收敛速度更快，收敛精度更高。

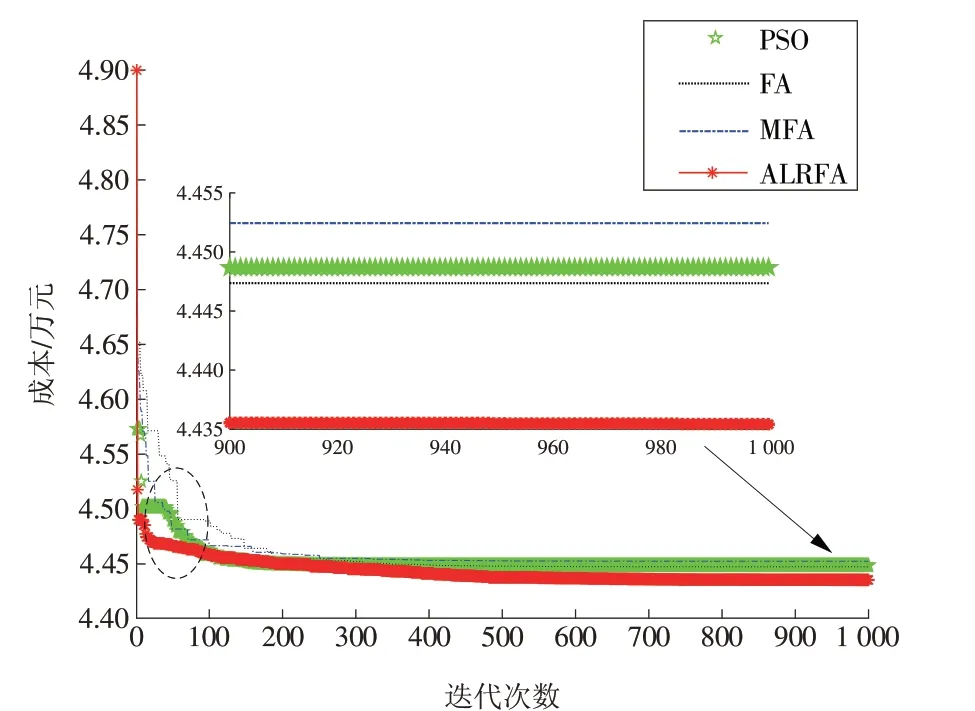
图4 各算法的收敛特性Fig.4 Convergence characteristics of different algorithms

通常情况下，启发式算法的运行结果都会表现出不稳定性，这是由于算法在每次优化运行中对模型的初始化和算法内部结构的随机参数（如高斯分布矢量e）都存在差异。为了验证所提ALRFA 的稳定性，采用4 种优化算法进行了20 次独立试验，各算法的收敛指标见表1。

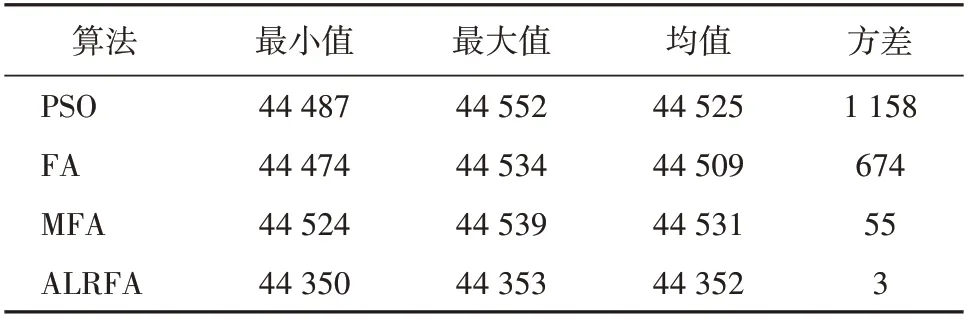
表1 各算法的收敛指标统计结果Table 1 Convergence results of different algorithms元

由表1 可知，相比于其他启发式算法，ALRFA的均值和方差明显更小，这表明ALRFA 不仅提高了算法的收敛精度及收敛速度，而且还提高了稳定性。

3.3 仿真结果分析

为进一步验证所构建MES 联合优化模型的有效性，结合ALRFA 对MES 的优化模型进行进一步分析。风力/光伏发电机组的发电功率以及实际被调用的风电/光电功率如图5所示，BESS的充放电功率（正为充电，负为放电）和SOC如图6所示，从主电网的购电量、向主电网的售电量和燃气轮机的发电量如图7 所示。为了验证MES 的经济性，本文综合对比了不含新能源发电站的多能源系统（Multi-Energy System without Renewable Energy Generation，MESWREG）、不含电池储能装置的多能源系统（Multi-Energy System without Battery Energy Storage System，MESWBESS）和CCHP 的分时运行成本，见表2。

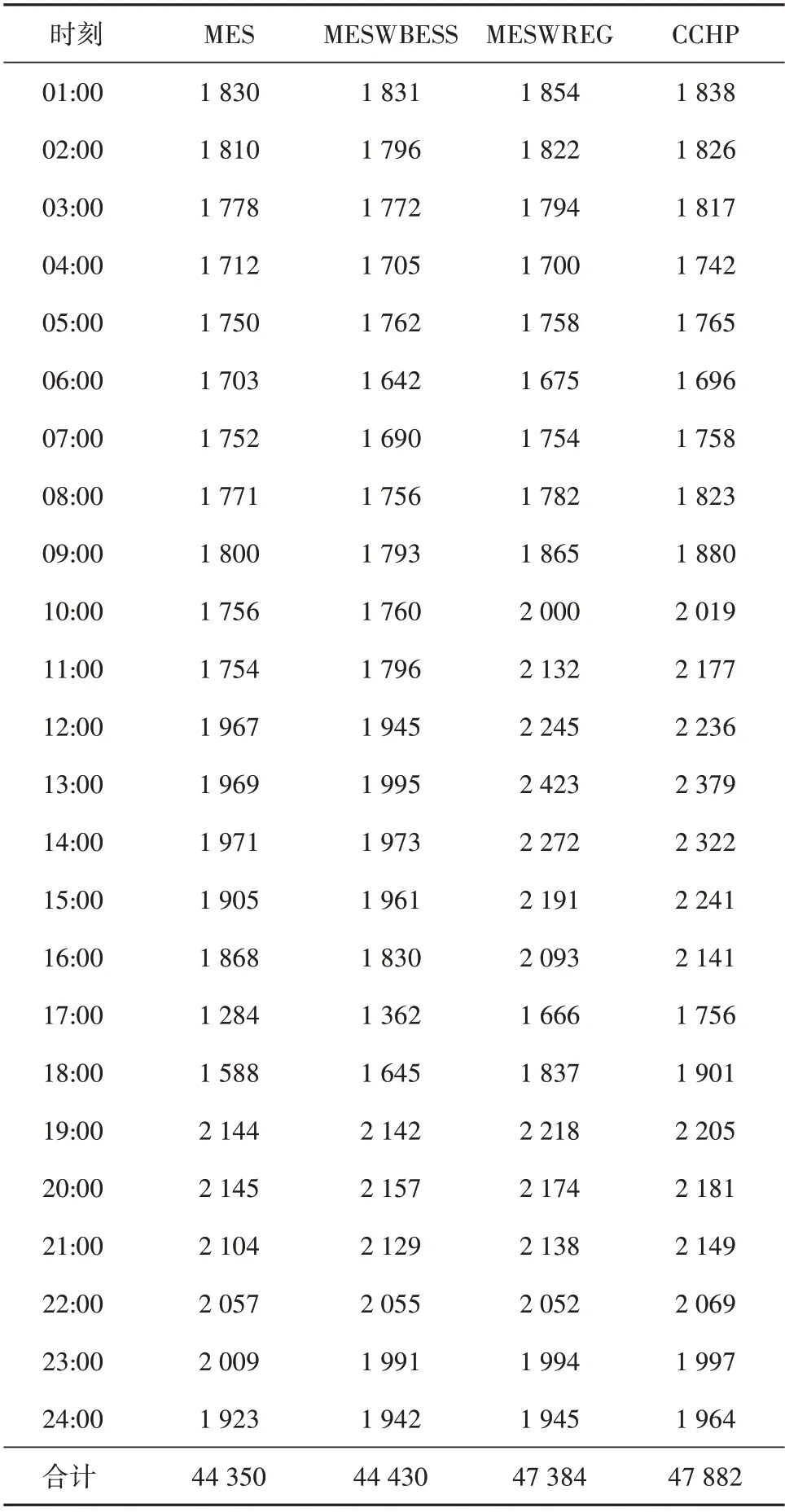
表2 不同系统的分时运行成本Table 2 Hourly operational costs of various systems元

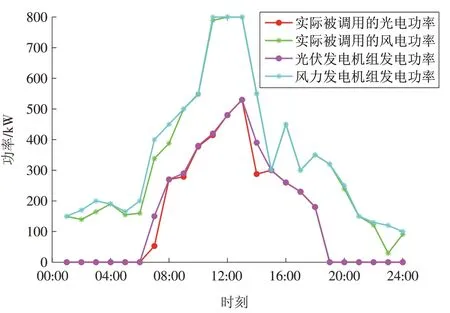
图5 新能源发电站分时发电功率曲线Fig.5 Curves of hourly power outputs from new energy power plants

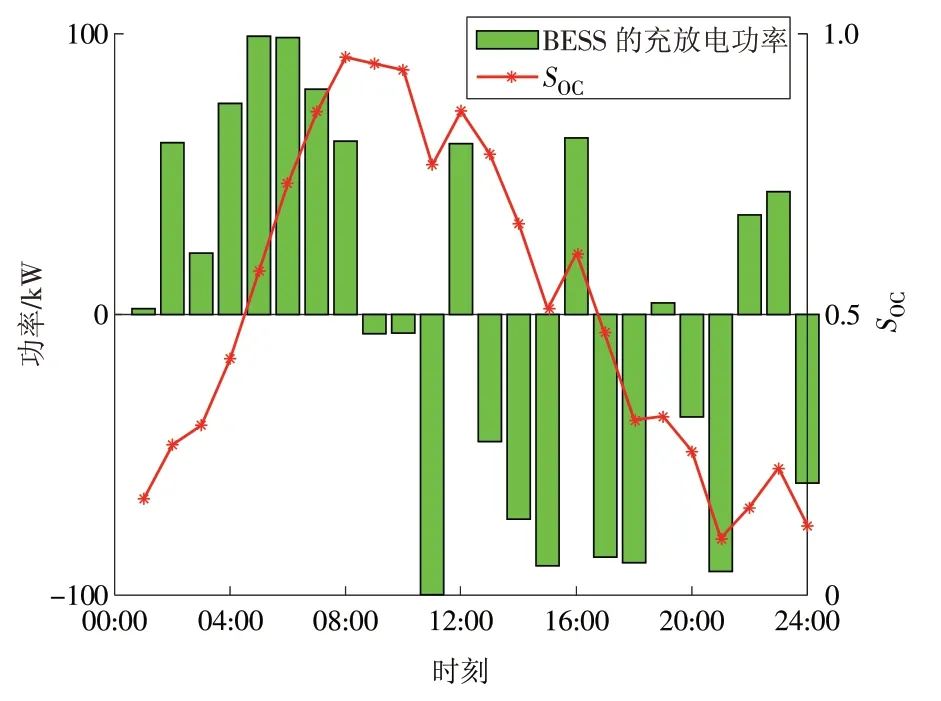
图6 电池储能装置分时充放电功率曲线及充电状态Fig.6 Curves of the hourly charge-discharge power and SOC of a BESS

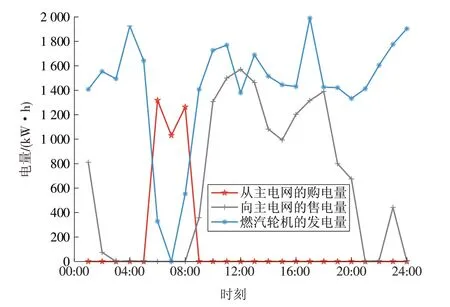
图7 主电网和燃气轮机分时电量曲线Fig.7 Hourly power generations and consumptions of power grid and a gas turbine

由图5 可知：实际被调用的风力/光伏发电总功率分别为8 022，3 662 kW；弃风弃光的总功率（风力/光伏发电机组的总功率-实际被调用的风力/光伏发电总功率）分别为373，218 kW；02：00—08：00弃风弃光功率较大且弃风弃光功率变化趋势接近一致。02：00—08：00 弃风弃光功率较大的主要原因是用户处于低冷/电负荷的条件下（如图3 所示），当向主电网的售电价格比风力/光伏发电机组的单位发电成本低时，MES剩余电量（弃风弃光功率）产生的运行成本将高于向主电网的售电收入，因而MES 出现了较大的弃风弃光功率。弃风弃光功率的变化趋势接近一致是由于风力发电机组的成本系数和光伏发电机组的成本系数接近一致。

由图6可知：08：00前BESS处于充电状态（SOC从0.17 变化到0.96），且06：00—08：00 的充电功率最大，这主要是由于08：00 之前向主电网的售电价格比大部分时刻都低，06：00—08：00 的价格最低。此外，通过图6 还可发现：除12：00，16：00 及19：00外，10：00—21：00，BESS的SOC曲线呈下降趋势，这主要是因为10：00—21：00 向主电网的售电价格比大部分时刻都高，因此BESS 处于放电状态。但受销售电价、最大放电功率、容量、退化成本等因素影响，BESS在12：00，16：00及19：00处于充电状态。

由图7可知：05：00之前，从主电网的购电量、向主电网的售电量和燃气轮机的发电量平均值分别为0，178，1 605 kW·h；06：00—08：00，从主电网的购电量、向主电网的售电量和汽轮机的发电量平均值分别为1 204，0，294 kW·h。对比01：00—05：00与06：00—08：00，从主电网的购电量和向主电网的售电量发生了相反的变化，且燃气轮机的发电量减少了1 301 kW·h，这主要是由于06：00—08：00 的电价变低且低于燃气轮机的燃气成本，主电网、光伏发电机组和风力发电机组承担了主要的电负荷和冷负荷。

值得注意的是，由于存在冷热负荷平衡，若MES 的运行成本小于向主电网的售电成本，为了保证不破坏硬约束（引入高惩罚因子），燃气轮机不会出现满发情况。09：00—20：00，向主电网的售电量平均值为1 138 kW·h，比01：00—08：00 的售电量平均值高了近10 倍，主要原因是09：00—20：00 的电价变高且高于燃气轮机的燃气成本，燃气轮机、BESS、风力发电机组和光伏发电机组可满足MES冷热电负荷需求，MES的剩余电量将售卖到主电网。

通过表2 可知：MES，MESWBESS，MESWREG和CCHP 的运行成本分别为44 350，44 430，47 384，47 882 元，MES 运行成本最低。MES 比MESWBESS的运行成本低的原因为：（1）BESS 根据不同电价信号对电能进行充放，实现峰谷差套利；（2）BESS对弃风弃光进行存储，提高了风电和光伏的使用率。MES 比MESWBESS 运行成本低的原因是：通过使用风力/光伏发电机组，一方面减少了从主电网的购电成本及燃气轮机的燃气成本，另一方面减少了碳排放的惩罚成本。MES比CCHP 的运行成本低的主要原因是新能源发电站、BESS 以及CCHP 之间的相互协调运行，提高了系统的运行效率。

4 结束语

本文构建了以新能源发电站、BESS 及CCHP 为主要承载对象的联合优化模型，提出了一种ALRFA，结合某园区冷热电负荷进行了算例分析，结果显示：（1）ALRFA 通过引入自适应学习速率参数，避免出现陷入局部最优和收敛速度慢问题，从而提高了寻优速度；（2）所构建的多能源系统通过峰谷套利、减少碳排放以及风光消纳方式提高了经济性，验证了所提联合优化模型在未来电力市场的应用潜力。