综合智慧能源系统中抽水蓄能电站两部制电价研究

李华，郑洪纬，周博文*，李广地，杨波

（东北大学a.信息科学与工程学院；b.辽宁省综合能源优化与安全运行重点实验室，沈阳 110819）

0 引言

随着国家“双碳”目标的提出，构建以新能源为主体的综合智慧能源系统是能源电力行业的重要研究方向［1］。新能源高比例、大规模的接入，迫切需要发展储能，以提升电力系统灵活调节能力和电能存储能力［2-3］。抽水蓄能作为目前公认的最安全、稳定、环保的储能方式，发展势头良好，发展潜力巨大［4］。我国当前正处在电力市场改革的初期阶段，两部制电价是国家发展和改革委员会在《关于完善抽水蓄能电站价格形成机制有关问题的通知》中明确提出的电价政策，不仅能促进抽水蓄能健康发展，也是深化电力市场改革的必要手段［5］。

随着国内对低碳减排的逐渐重视以及“双碳”目标的提出，符合减排要求的可再生能源正在大规模接入电网，合理、有效地促进可再生能源消纳成为储能系统的一个重要研究内容。文献［6］对能量与功率混合储能系统参与辅助风电消纳进行了可行性分析。文献［7］进一步归纳了各种储能技术的能量转换效率、功率密度等参数以及其在促进分布式可再生能源消纳方面的应用情况。文献［8］考虑火电和抽水蓄能各自参与风电消纳的边际成本效益，提出了一种基于分段电价的风电消纳方法。文献［9］提出了一种对区域电网风电消纳能力进行有效评估的方法。文献［10］基于园区的优化控制策略逻辑框架,充分考虑储能系统的作用,建立了以经济性和碳排放约束为目标函数、以各种负荷供需平衡和耦合设备运行限制为约束的多时间尺度优化模型。为了充分利用区域电网的新能源消纳能力，文献［11］提出一种基于分布式能量β分布最小置信区间的包括储能、风力发电、光伏发电的主动配电网鲁棒最优运行方法。这些研究大多从提升储能系统参与可再生能源消纳积极性的角度出发，以降低弃风弃光率为目标，没有充分考虑储能作为主体的利益需求。

研究适用于抽水蓄能电站的合理电价机制和电力市场竞价模式对其参与电力市场竞争有着重要意义［12］。文献［13-14］研究了多种形式储能系统参与电力市场竞争的运行策略。文献［15-18］提出了电力市场中储能系统的多级协同规划控制，实现了储能设备的最优化配置运行。文献［19］提出多风电与抽水蓄能电站联合参与现货市场的模式。文献［20］考虑到专项工程输电价格难以核定的问题，提出了面向电力现货市场的两部制电价优化模型。文献［21］在电价优化模型的基础上研究了两部制的最优定价工具并应用于风电场，证实了将能量和容量分开定价的必要性。但上述文献的研究只考虑了储能参与电力市场的收益，并未考虑储能在促进新能源消纳的同时降低对化石能源消耗、促进低碳运行的可行性。

针对以上问题，本文研究可再生能源消纳场景下的抽水蓄能两部制电价机制，通过经营期电价法核定容量电价；考虑“抽水蓄能+风电”联合运行模式，利用风电的峰谷价差求解机组最优运行策略，通过价格需求关系和变动成本补偿得到具有竞争力的电量电价；对各机组的出力进行分析，证明抽水蓄能促进风电消纳的高效性和系统低碳运行的可行性，以保障综合智慧能源系统和抽水蓄能电站健康有序地发展。

1 综合智慧能源系统和两部制电价

1.1 综合智慧能源系统

综合智慧能源系统是一种新型的一体化能源系统，它在一定区域内利用先进的物理信息技术和创新管理模式，整合区域内多种能源，实现子系统之间的优化运行和协同管理，有效提升能源利用效率，促进能源的可持续发展。信息技术控制系统中源、网、荷、储能源供应环节之间的协同和互动是实现综合智慧能源革命的关键部分，其中储能系统凭借削峰填谷和调频调压等能力，成为综合智慧能源系统稳定运行的基石。抽水蓄能作为目前全球最成熟的储能形式，发展面临诸多难题，两部制电价机制的完善和应用为电价机制缺失的难题提供了新的解决思路。

1.2 两部制电价

两部制电价由容量电价和电量电价两部分组成。容量电价主要用来补偿电站的固定成本，包括电站投资、还贷、折旧等多种经济因素，其可按变压器容量计算，也可按最大需求量计算。容量电价的制定有政府定价、市场竞价、协商等几种方式。而电量电价主要用来补偿电站的变动成本，与材料费、人工费等密切相关。电量电费是根据实际用电数计算的电费，电量电价能够体现发电企业一定的竞争力，通常在市场竞争中得以形成。

在综合智慧能源系统中，两部制电价中的容量电价能够适当补偿容量成本，在一定程度上确保收回抽水蓄能电站的建设投资成本，保障机组不会出现较大亏损，故同一抽水蓄能电站的容量电价基本不发生变化；在没有容量成本负担的情况下，电量电价可以更准确地反映抽水蓄能电站的边际成本，保证发电机组在市场中的竞争更加公平充分，有利于其稳定运行。在此基础上，两部制电价能促进发电企业加强内部管理，提高企业运营效率，促使电力行业发电侧电价向完全竞争性电价平稳过渡，因此，在电力市场建设初期对抽水蓄能电站实行两部制电价是深化电力市场改革的必要手段。两部制电价符合改革发展要求，具有降低抽水蓄能电站参与电力市场交易的风险、促进发电侧公平交易、发挥市场机制资源配置优势等优点。

影响两部制电价的因素有很多，包括电能需求关系因素、自然资源的时间因素和季节因素、社会与政策因素等，因此，需要对抽水蓄能电站的用电和发电过程进行深入分析，其中，机组运行策略、可再生能源出力和季节性蓄水量变化均会对两部制电价产生影响。

2 抽水蓄能电站两部制电价制定策略建模

2.1 容量电价核定方法

本文依据经营期定价法确定容量电价［22］，经营期定价法的主要依据是动态经济性评价方法中的净现值法。

抽水蓄能电站建成投产后，每年的净现金流量为

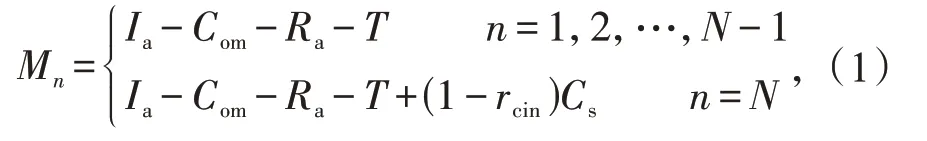
式中：N为抽水蓄能电站运行与使用年限；Ia为含税年售电收入；Com为年运行维护费；Ra为年还贷额；T为年缴税总额；Cs为固定资产残值变卖收入；rcin为企业所得税税率。

含税年售电收入由增值税费和不含税年售电收入组成

式中：I为不含税年售电收入；Tvat为增值税费。

年缴税总额由增值税、销售税和企业所得税组成，各类税费由对应税率计算得到。

式中：rvat为增值税税率；rsal为销售税税率；Tsal为销售税费；Tcin为企业所得税费；Cd为年折旧额。

抽水蓄能电站建设期现金流出量为建设期动态投资总额与贷款额的差值，建设期现金流出量与运行年限内全部现金流入量相等。

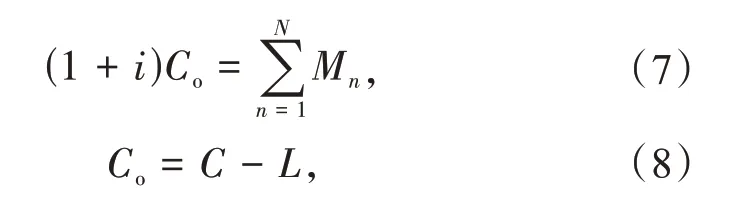
式中：Co为建设期现金流出量；i为内部合理收益率；C为动态投资总额；L为贷款总额。

最后得到单位装机容量的容量电价为

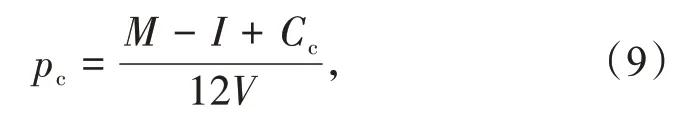
式中：pc为单位装机容量的容量电价；Cc为年抽水成本；V为装机容量；M为经营期内净现金流量总额。

年抽水成本和含税年售电收入在下节进行计算，容量电价具体求解流程如图1所示。

图1 容量电价求解流程Fig.1 Solving process of capacity price

2.2 电量电价制定策略建模

以风电为例，抽水蓄能电站与风电场联合参与电力市场优化调度模型建立在一个风电与燃煤发电系统引入抽水蓄能电站的新系统中。原系统的风力发电侧有一定的弃风率，新系统中抽水蓄能电站在合适的时间对弃风产生的电量进行储存再利用。

本文在研究抽水蓄能电站与风电场联合参与电力市场时抽水蓄能发电电价的问题时，以原电力系统引入抽水蓄能电站之后的新系统发电总成本减少量最大（式10）和抽水蓄能电站抽水成本最小（式11）为优化目标，得到日最优发电策略后，根据变动成本的合理回收原则，制定抽水蓄能的分时电价。

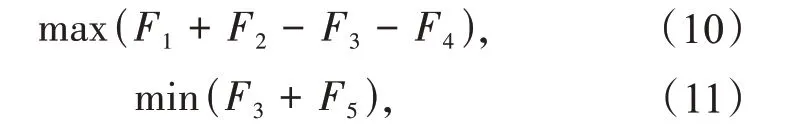
式中：F1为燃煤机组发电成本减少量；F2为原发电系统的弃风惩罚；F3为抽水蓄能机组启停成本；F4为抽水蓄能损耗能量成本增量；F5为抽水蓄能电站抽水成本。

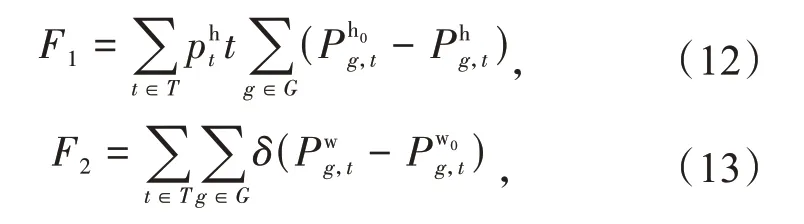
该模型的约束条件主要由抽水蓄能机组、燃煤机组和风电机组的功率平衡和运行特性组成，具体包括抽水蓄能电站的抽发功率约束（式（17）—（18））、抽发功率平衡约束（式（19））和抽发状态约束（式（20））、电站上库容与下库容约束（式（21）—（22））、电站发电电量和抽水电量约束（式（23）—（24））、抽水电价与风电电价相同（式（25））、风电机组出力约束（式（26））、燃煤机组出力约束（式（27））、机组爬坡约束（式（28）—（29））、系统电功率平衡约束（式（30）—（31））。

2.3 求解流程

本文利用在遗传算法基础上提出的NSGA-Ⅱ算法实现该多目标优化问题的求解，具体流程如下。

（1）确定种群规模N和最大迭代次数G，并随机初始化种群。

（2）根据约束违反值分离可行解与不可行解，利用可行解构造非支配解集。

（3）进行非支配排序，计算每个个体p的被支配个数np和该个体支配的解的集合Sp，得到不同Pareto等级下的个体集合，完成种群等级的划分。

（4）根据每个目标函数，对多个Pareto 等级下的个体进行排序，并计算每个等级的个体拥挤度，其中排序边界的拥挤度设为无穷大。

（5）设定交叉概率和变异概率，对个体的所有变量进行N/2 次模拟二项式交叉和N次多项式变异操作，得到子代种群。

（6）将父代种群与子代种群合并，对新种群的个体进行快速非支配排序和拥挤度计算。

（7）根据精英保留策略，将全部个体按Pareto 等级从低到高和个体拥挤度从大到小排列，以种群规模为最大保留值，生成新的父代种群。

（8）判断是否达到最大迭代次数，若满足要求则停止迭代，否则跳转到（5）继续循环。

求解基本流程如图2所示。在可行区域内对算法所得的Pareto 最优解集进行选择，最终得到该多目标问题的Pareto最优解。

图2 电量电价求解流程Fig.2 Solving process of energy price

根据模型求解得到Pareto 最优解所对应的日最优发电策略后，在抽水蓄能的发电时段回收日内抽水时段的购电成本，根据负荷需求量与电价的供需关系制定电量电价，从而引导用户在负荷低谷时段购电，增加风电消纳量，降低储能成本。

价格需求关系近似为一次函数，将最低电价设置为200 元/（MW·h），即k1=200，根据式（32）和式（33）可以计算出k2，从而得到发电时段的电量电价。

式中：k1，k2为价格需求系数；pt为分时段电量电价。

在抽水蓄能的抽水时段，“抽水蓄能+风能”联合系统优先采用风电供电，其次采用火电供电，以补偿变动成本为主要目的制定电量电价。综上，抽水蓄能电量电价为

3 算例分析

3.1 结果分析

为了得到抽水蓄能电站与风电场联合运行的抽发策略，进而求出抽水蓄能电站的容量电价和电量电价并验证该策略的有效性，采用如下算例系统：抽水蓄能电站装机容量为300 MW，上、下水库库容上限为3 000 万m3，水库初始水量为容量上限的50%，平均能量转化效率为75%，水电机组平均耗水率为4 000 m3/（MW·h）；风电装机容量为1 200 MW，风速及发电功率采用国内某风电场数据；火电装机容量为2 000 MW；时间尺度设为1 h，电价数据参考其他文献的相关研究结果。利用NSGA-II 算法对该多目标优化问题进行求解，种群规模设为50，最大迭代次数设为200，交叉概率为0.8，变异概率为1/24。仿真计算在Python 3.8 中进行，最终得到该算例下的抽水蓄能电站日最优抽发策略。

由图3 可以看出：抽水蓄能电站抽水时间主要集中在01：00—07：00，13：00—15：00，而01：00—07：00 时抽水功率达到最大；发电时间主要集中在09：00—11：00 和18：00—22：00，在09：00—11：00，18：00—22：00 达到最大发电功率；11：00—13：00，15：00—18：00 以及22：00—23：00 抽水蓄能机组处于待机状态。得到抽水蓄能合理抽发策略以后，可以得到一天的抽水量和发电量，再根据保证抽水蓄能电站抽水成本合理疏导的原则，可以计算出一天的预计发电总收益，根据总抽水成本和用电负荷供需关系，可以得到联合供电系统分时段电量电价。

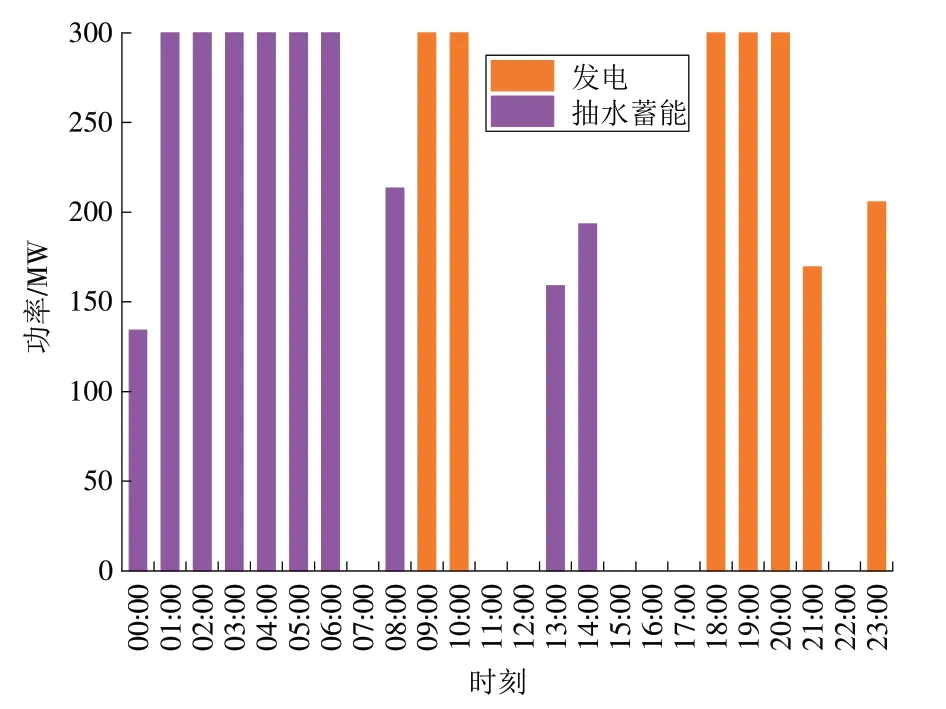
图3 抽水蓄能电站日最优抽发策略Fig.3 Daily optimal pumping and generation strategy of the pumped storage power plant

在不含抽水蓄能电站的原系统以及引入抽水蓄能电站的新系统中，风电、火电和抽水蓄能的出力如图4所示。

如图4a 所示，原系统主要由火电供电，一部分风电参与供电，由于风电的成本和出力不确定等原因，风电消纳量较低。如图4b 所示，在引入抽水蓄能的新系统中，风电消纳量显著增加，这是因为抽水蓄能电站在风电出力较大且利用率低的01：00—07：00 进行抽水蓄能，显著增加了风电的消纳量；与此同时，抽水蓄能电站在用电负荷较大的09：00—11：00 和18：00—22：00 进行发电，降低了火电的高峰期出力，缓解了电力系统用电高峰所带来的一系列风险。由此可见，抽水蓄能电站在消纳风电和降低火电出力方面有着巨大优势，有利于促进综合智慧能源系统低碳运行，实现“双碳”目标。

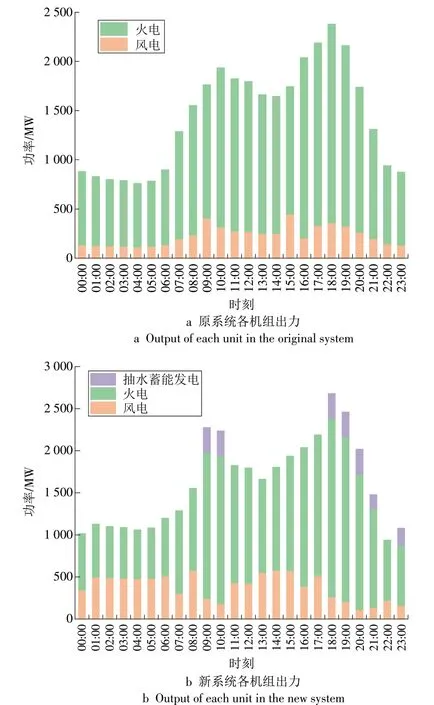
图4 不同系统中各机组出力Fig.4 Outputs of different units in the system

基于上文的抽水蓄能机组抽发策略，可以得到抽水蓄能电站年发电总量，进而得到含税年售电收入。其中抽水蓄能电站运行年限设定为20 a，建设期现金流出量设定为20 亿元，装机容量为300 MW，年运行维护费为7 万元/MW，合理收益率为8%，税率全部按照国家相关标准计算。容量电费采用合约形式以年或月为单位收取，也可以均分到单位小时得到相应的容量电价，计算得抽水蓄能机组的容量电价为2.79 万元/（MW·月），再根据抽水蓄能机组实际运行容量与抽发电量，得到单位电量的容量电价。电量分时电价与容量平均电价在单位调度周期内为加和关系，最终得到单位调度周期内的两部制电价，见表1。

由表1 可见，抽水蓄能电站主要在用电负荷较大且其他发电单位电价较高时发电，傍晚时达到一天内的用电高峰，这期间抽水蓄能电量电价也相应较高，日电量电价曲线有2 个峰值，分别在08：00—10：00 和18：00—20：00。其他阶段用户用电需求减少，抽水蓄能发电量减少，电量电价也相应较低，日电量电价总体在02：00—04：00 和11：00—12：00 时段于低谷。根据求解的日容量电价结果，结合抽水蓄能机组日工作时间以及抽水发电总量，可以确定单位电量的容量电价，最终保证每日的容量电价总收入可以补偿抽水蓄能机组的容量成本。

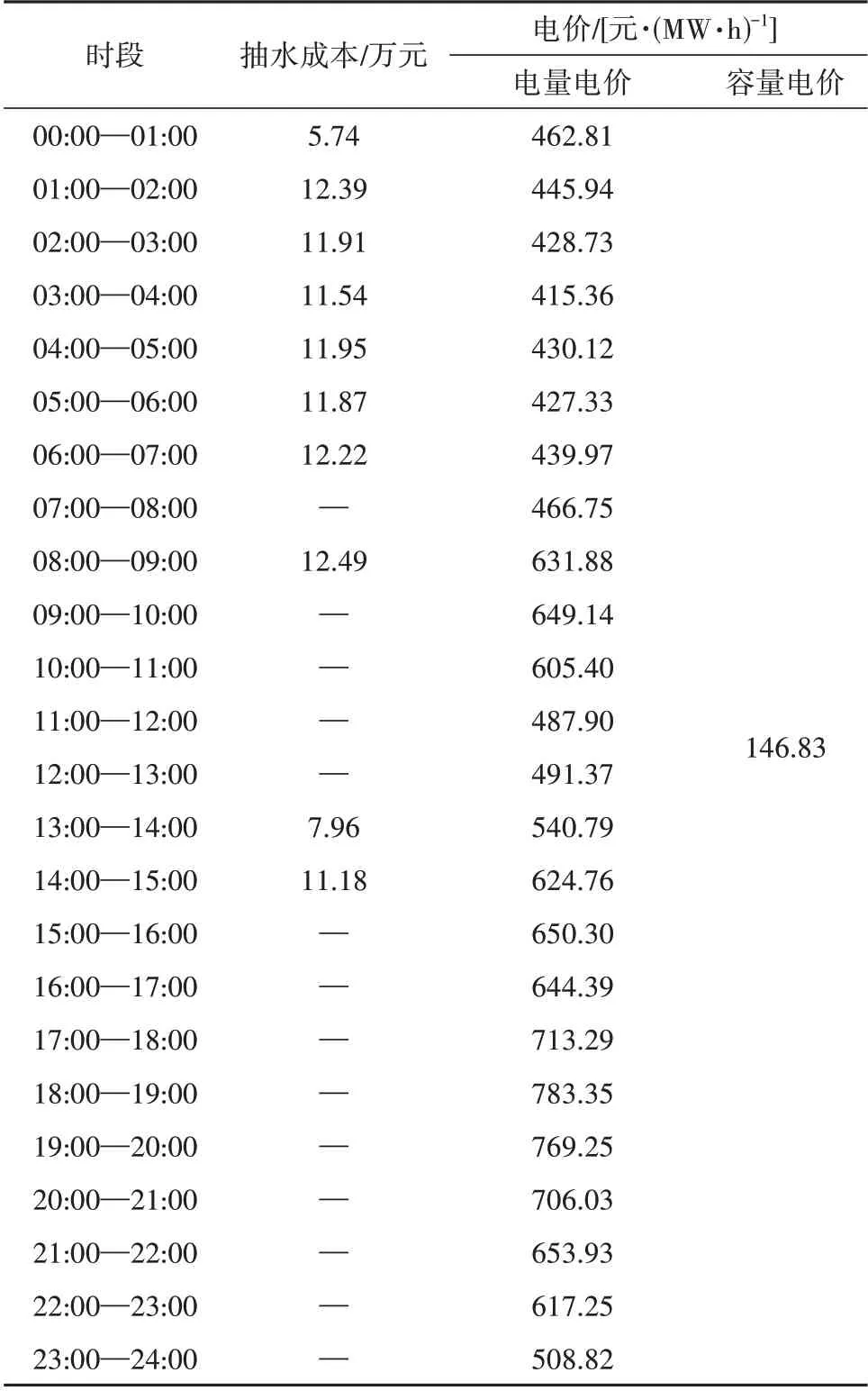
表1 抽水蓄能两部制电价Table 1 Two-part tariff strategy for pumped storage power plants

3.2 两部制电价分析

在该算例系统中，影响抽水蓄能电站电量电价的根本因素是抽水成本。抽水成本取决于风电电价与风电消纳量，为了研究抽水蓄能电价与风电消纳量的关系，本节通过设置4 个算例场景来对比说明风电消纳量对抽水蓄能两部制电价的影响，场景设置见表2。

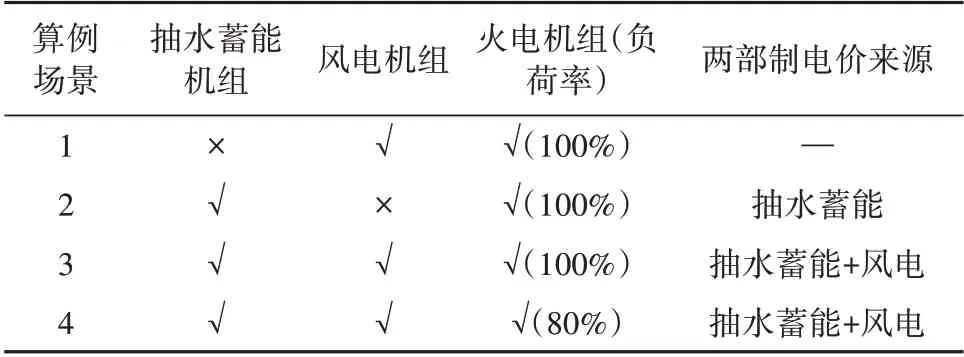
表2 算例场景设置Table 2 Settings under different scenarios

为了比较抽水蓄能独立参与电力市场以及与风电联合参与电力市场的两部制电价定价机制的差别，列出场景2，3，4 的抽水蓄能容量电价和电量电价以及火电、风电价格，如图5所示。

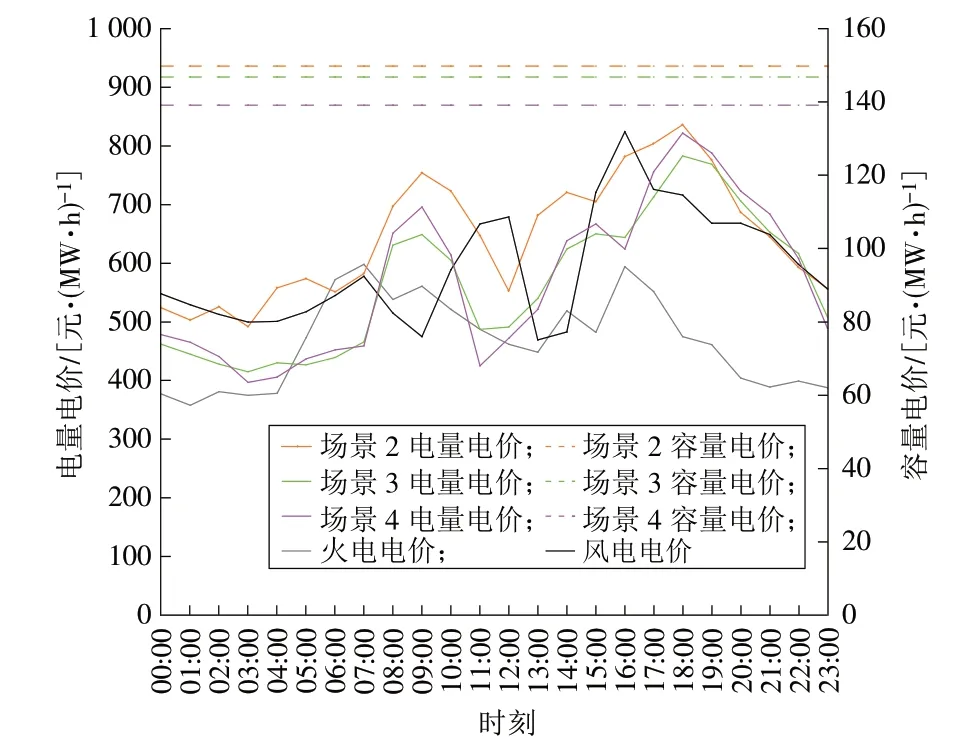
图5 各场景的两部制电价Fig.5 Application scenarios of the two-part tariffs

场景2 中，系统含抽水蓄能机组但不含风电机组，抽水蓄能的抽水电量多来自火电机组，成本较高，导致整体电量电价相对较高；同时，由于火电的峰谷价差（344 元/（MW·h））较小，使得抽水蓄能电量电价峰谷差较小。根据容量电价计算公式计算得出的容量电价相比于其他场景是最高的，这是由于在没有风电机组参与的情况下，抽水蓄能电站的抽水电量主要来自火电机组，抽水成本相对较高。

场景3中抽水蓄能机组与风电机组同时参与电能调度，由于容量电价主要用于补偿抽水蓄能电站的建设投资等固定成本，所以其定价机制不发生变化；而电量电价相比于场景2发生较大变化，这是由于在场景2 和场景3 中，抽水蓄能电站的抽水电量来源分别是风电机组与火电机组，2 个场景下的抽水蓄能抽发策略不同，会使得定价结果有较大不同；场景3中，抽水蓄能可以在风电电价较低的时间段抽水，极大地降低了抽水成本，其容量电价与电量电价相比于场景2 均有所降低，且抽水电量主要由电价波动较大的风电提供，所以电量电价的峰谷差增大，为368 元/（MW·h）。总的来说，相比于抽水蓄能电站单独参与电力市场交易，抽水蓄能电站联合风电参与电力市场交易的容量电价和电量电价都有一定程度的降低，参与电力市场的竞争力更强；同时，由于积极参与了新能源消纳，促进了综合智慧能源系统低碳运行。

场景4中，火电机组出力减少，抽水蓄能的出力增加，相比于场景3，抽水蓄能电量电价的峰谷差进一步拉大，达到425 元/（MW·h），高峰期电量电价最高达到822 元/（MW·h），容量电价相比于场景3 有小幅降低。为了进一步分析不同场景下抽水成本与两部制电价的关系，列出4 个场景下的平均抽水成本、平均容量电价和平均电量电价，如图6所示。

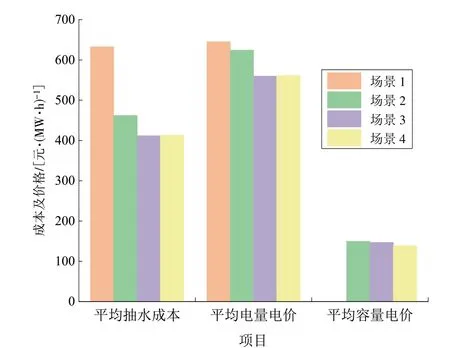
图6 各场景的抽水成本与两部制电价对比Fig.6 Comparison of water pumping cost and two-part tariff under each scenario

由图6 可见，在无抽水蓄能参与的场景1 中，相同抽水电量下，风电的发电成本明显高于其他3 个场景，在考虑损耗的情况下，平均抽水成本（632.64元/（MW·h））与平均电量电价（645.29 元/（MW·h））也是最高的。

场景2 中，系统含抽水蓄能机组但不含风电机组，由于火电价格波动较小，抽水蓄能机组难以实现“低电价抽水、高电价放电”的运行策略，导致其日总抽水成本相较于场景3 高12.61 万元，平均电量电价与平均容量电价分别比场景3 高64.27，2.98 元/（MW·h）；在场景3中，由于抽水蓄能在风电电价低时抽水储能，用户用电负荷高时发电，所以其经济性较好，电站的总抽水成本、平均抽水成本、平均电量电价和平均容量电价均优于场景2。由此可见，“抽水蓄能+风电”的联合运行模式可以显著提高电力系统的经济性。

相比于场景3，场景4 的火电出力降低，负荷侧对风储联合系统的供电需求增大，因此需要适当增大抽水蓄能装机容量。在抽水电量增加的情况下，日总抽水成本增加8.53 万元，平均电量电价也小幅增加了1.49 元/（MW·h），但由于总发电量增加，用以补偿固定成本的容量电价相较于场景3 降低了7.72 元/（MW·h）。显然，抽水蓄能电站的装机容量对抽水成本有一定的影响，由此推测，抽水蓄能电站的自身因素如装机容量、水库库容上限、日初始库容、抽水效率等也可能会对抽水成本产生影响。

4 结论

本文旨在研究“双碳”目标下抽水蓄能电站的两部制电价，建立了抽水蓄能电站与风电场联合运行的优化调度模型，找到抽水蓄能的最优抽发策略并计算出其容量电价与电量电价。通过算例分析其参与新能源消纳的可行性，并验证该策略有利于提高抽水蓄能电站运行的经济性和可靠性，得到以下结论。

（1）引入抽水蓄能电站的系统可以显著增加新能源消纳量，降低化石能源出力，促进综合智慧能源系统低碳运行，助力实现“双碳”目标。

（2）抽水蓄能电站的电量电价主要由抽水成本决定，在抽水蓄能电站与风电场联合运行的系统中，电量电价平均为560.00 元/（MW·h），发电时间主要集中在09：00—11：00和18：00—22：00；容量电价主要由建设期资金投入与总发电量决定，在该系统中，容量电价为146.83 元/（MW·h）。

（3）在不同场景下，抽水蓄能电站的抽水成本与两部制电价会随着风电消纳量和火电供电占比的不同而发生改变，适量风电的消纳会显著降低电价，而火电出力变化对电价的影响较小。

抽水蓄能电站自身因素如装机容量、水库库容上限、日初始库容、抽水效率等也可能影响电价进而对新能源消纳量有影响，后续可以在该方向继续进行数据验证，找出抽水蓄能电站最佳建设容量，提高综合智慧能源系统的经济性。