基于纳什议价的共享储能能源互联网络双目标优化

冶兆年，赵长禄，王永真，2*，韩恺，2，刘超凡，韩俊涛

（1.北京理工大学机械与车辆学院，北京 100081；2.北京理工大学重庆创新中心，重庆 401120）

0 引言

随着碳达峰、碳中和战略的提出，以新能源为主体的“互联网+智慧能源”逐渐实现技术与产业的融合［1］，到2030 年，我国风电、太阳能发电总装机容量将达到1.2 TW 以上［2］。但是，新能源的加入加剧了能源系统供应侧多异质能流的非线性耦合问题以及负荷需求时空不匹配问题；同时，风光不确定性带来了供应侧可再生能源的不确定性［3］。在风电和光伏装机量不断提升的大背景下，发展储能技术是解决供需匹配问题、减小风光波动性对电网冲击的必要途径［4］。

虽然储能是解决上述问题的必经之路，但目前储能电站依靠单一峰谷套利很难获得投资收益。为克服传统储能模式经济效益不佳的缺点，国内外学者提出了“共享储能（Shared Energy Storage，SES）”的商业模式，即利用共享储能为一个区域内的多个用户提供高容量储能系统，而不是为用户设立单独的储能系统，从而消除个人购买、维护、维修和更换电池的成本［5］。王仕俊等［6］针对社区综合能源系统，提出了在拥有共享储能、热电联供以及光伏电源的情况下，居民用户日前调度安排方法，通过协同优化方法对用户用能方式进行优化，并利用改进粒子群算法对所建立模型进行求解；Lombardi等［7］对比了不同电池选型对共享储能系统的影响，得出全钒液流电池适用于长期储存进行季节调峰，锂电池适合频繁充放电系统的结论；潘倩华等［8］阐述了工业园区共享储能配置与运行的双层规划，分析了园区内存在的不确定性问题，基于园区用电日负荷曲线，采用鲁棒优化算法和上下层模型迭代达到利益最大化，并结合实际算例验证了共享储能的可行性和优势；Szabó 等［9］提出了一个市场框架，将储能供应链作为一个独立的经营者，在能源市场上以最佳方式出售储能空间和交易能源；刘敦楠等［10］采用用户跟踪的模式对用户需求侧资源调节进行了研究，相比于参与峰谷分时电价需求响应模式，用户跟踪可再生能源曲线模式更为灵活，具有更多样的选择和电价决策权；Ziegler 等［11］从一次能源利用的视角对比了吸收式制冷机组与电制冷的优劣势。在多个用户之间成本博弈的问题上国内外学者也进行了诸多研究，帅轩越等［12-13］提出了一种多区域综合能源系统互联下的共享储能系统容量优化配置模型，采用双层优化对多个用户间的成本分配进行纳什议价；顾欣等［14］通过纳什议价模型采用用户负荷聚合商的方式实现了碳交易机制下的多微网协同运行。

共享储能项目随着“双碳”目标的确立迅速落地，在国外，美国加州萨克拉门托市政公用事业区(Sacramento Municipal Utility District，SMUD)［15］推出了共享储能计划，这是美国第1个共享储能计划，该计划允许SMUD 的商业客户投资异地储能系统，并在不安装独立储能系统的情况下节省能源成本；在国内，青海省鲁能海西州多能互补储能电站通过双边协商交易和市场竞价交易2 种模式，有效提升了系统调峰能力，增加了新能源发电并网，解决了新能源弃电问题［16］。

可以看出，计及共享储能的能源系统规划优化成为“双碳”愿景下能源系统向能源互联网发展的热点问题［17］。一方面，共享储能有望解决传统能源系统自建储能系统的高投资低回报问题；另一方面可以促进相互独立能源系统间的共享，实现能源的高效利用。目前，共享储能的研究还处于起步阶段，共享储能服务商与能源互联网间的规划调度多采用双层优化、粒子群算法等方式，其对能源互联网络与共享储能系统（Shared Energy Storage System，SESS）的优化不够科学；同时，分布式冷热电能源系统（Multi-Distributed Energy System，MDES）间的利益分配机制还不清晰，如规划与优化方法是SESS建立的关键，需要采取合适的方法确立SESS与分布式MDES 间的收益与成本博弈下的储能系统容量，确定容量下MDES 间的合作博弈也需要进行合理规划。

基于上述问题，本文提出基于纳什议价的共享储能能源互联网络双目标优化，并以1 个SESS 和4个MDES的模式为案例进行分析。为解决现有共享储能存在的储能收益与用户成本相悖的问题，提出基于Pareto 非劣解的双目标优化及调度方法，实现SESS 容量以及MDES 设备容量的优化；针对MDES间能量交互存在的合作博弈现象，采用交互收费和纳什议价2种模式，对MDES交互进行研究。

1 基于共享储能的MDES构型

1.1 SESS概述及模型建立

本文研究对象包含由4 个冷热电MDES 组成的能源互联网络、能源信息调度管控系统、SESS 以及配套的配电网、燃气网，如图1所示。假设用户仅在冬季有热负荷需求（少量的生活热水负荷不计），仅在夏季有冷负荷需求，冬季、夏季以及过渡季均存在电负荷需求，但不同的MDES 各季节需求有所不同。

如图1 所示，本文所述MDES 采用共享储能的建设运行模式，即通过SESS 同时为4 个MDES 提供容量与能量共享的电化学储能服务，共享储能运营商投资建设一定运营周期的储能设备，在不同时间为4 个MDES 分配不同的共享储能容量［7］。共享储能商业模式为：在MDES 向SESS 存储电能或使用SESS 内已储存的电能时收取流量费；同时，通过SESS 可实现MDES 之间的能量交互，此时费用仅在发生交互的2个MDES之间产生。

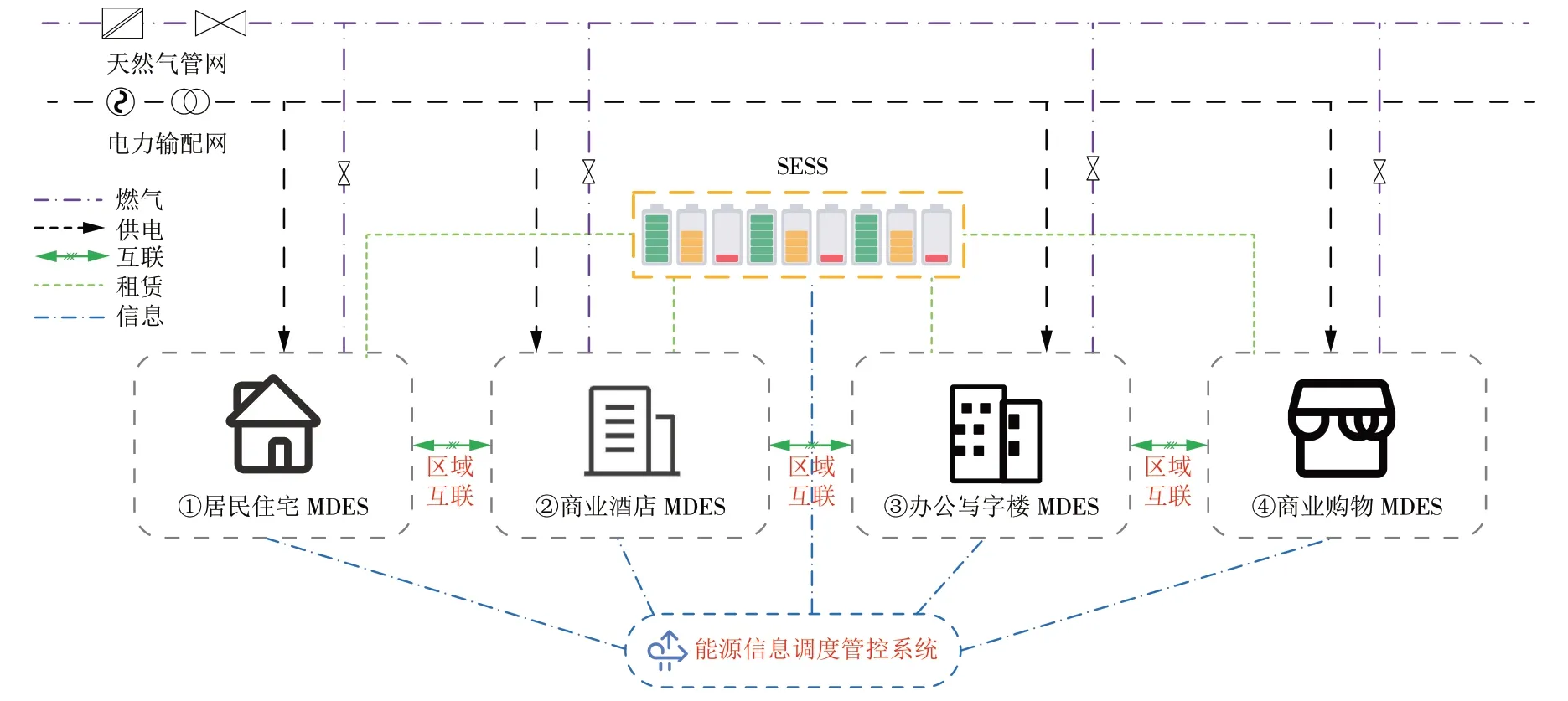
图1 共享储能能源互联网络Fig.1 Energy network with shared energy storage

1.1.1 SESS模型

SESS 为MDES 提供储能容量，在能源信息调度管控系统的调度下，通过收取MDES 利用储能容量进行充放电时的流量费用实现盈利，SESS 的收益GSESS由收入与成本决定［12］。

式中：CSESS1为SESS 收入；CSESS2为SESS 建设成本；CSESS3为SESS维护成本。

运行过程中SESS需满足以下约束

1.1.2 MDES间电能交互模型

MDES 间进行电能交互时，购电方需向售电方支付一定的购电费用

1.2 MDES模型及约束

单个冷热电MDES（以居民住宅MDES 为例）由光伏发电（Photovoltaic，PV）装置、热电联产（Combined Heat and Power，CHP）机组、电锅炉（Electric Boiler，EB）、吸收式制冷（Absorption Refrigeration，AC）机组、电压缩式制冷（Electric Compression Refrigeration，EC）机组等组成，其内部能量流动如图2所示。

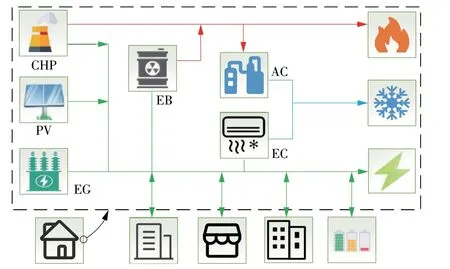
图2 MDES内部能量流动Fig.2 Energy flow in a MDES

在MDES 中，AC，EC 满足冷负荷需求，CHP，EB满足热负荷需求，CHP，PV 满足电负荷需求的同时可将冗余电量向其他系统出售或通过SESS 进行存储，MDES设备约束见表1。

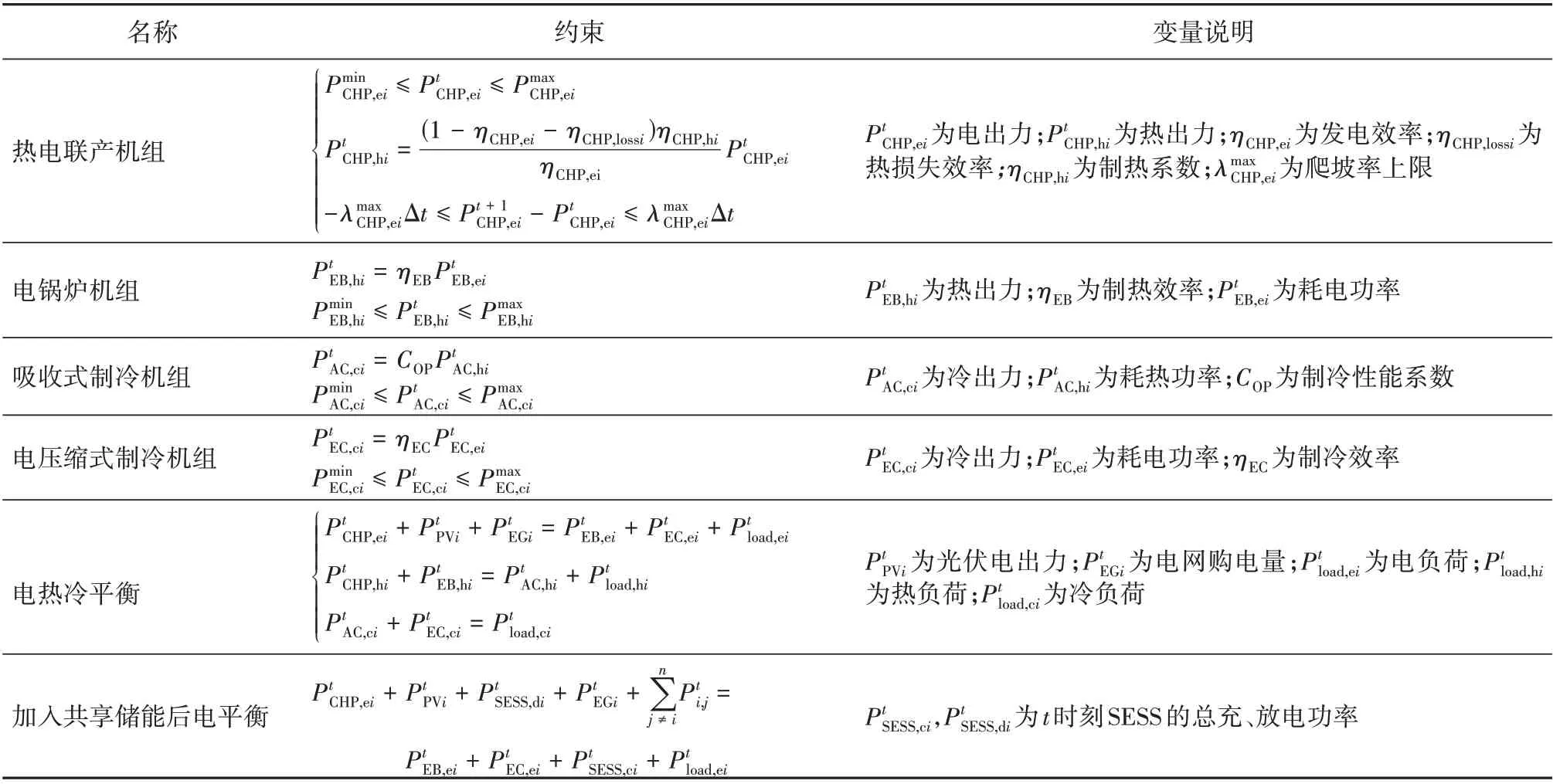
表1 MDES设备约束Table 1 Constraints on equipment of the MDES

在无共享储能的模式下，单个MDES 成本包括设备建设成本Cbi、设备维护成本Cmi、购电成本CEGi和购气成本Cgasi。

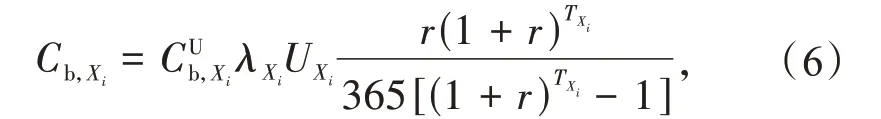
式中：Cb，Xi为第i个MDES 内设备X（CHP，EB，AC，EC，PV）的建设成本；为设备X的单位建设成本；UXi为设备X的装机规模；TXi为设备X的运营周期。

式中：Cm，Xi为设备X的维护成本；fm为维护成本与建设成本的比例系数。

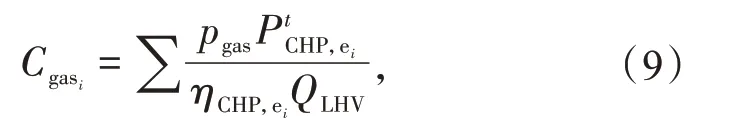
式中：pgas为天然气单价；QLHV为天然气低热值。

假设不计系统的施工、管网、前期规划等成本投入，MDES总成本CMDES_all可由下式求得

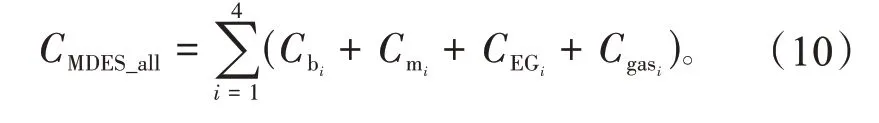
在共享储能接入的情况下，相较无共享储能的系统，第i个MDES 增加了与SESS 的交互成本CSESSi及与其他MDES的交互成本CI。

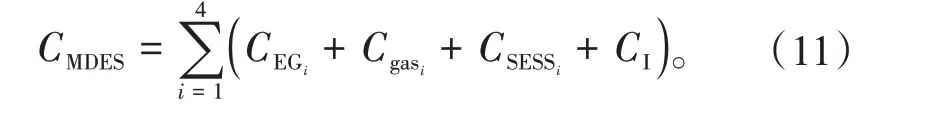
由于优化目标为MDES 的成本之和，可能会出现总成本最优但个别MDES 成本上升的情况，为保证各MDES的利益，需添加成本约束

式中：C'MDESi为无共享储能时第i个MDES 的运行成本；CMDESi为设置共享储能后第i个MDES 的运行成本。

2 多目标优化及求解

2.1 双目标优化及优化指标

共享储能能源互联网的规划和优化，不仅要考虑MDES 的运行成本，还要考虑SESS 的收益。本节采用非劣解的双目标优化进行计及共享储能的MDES 优化。优化的自变量为SESS 容量USESS、对应的设备逐时出力状态PXi以及独立系统的交互功率Pi，j。优化目标分别为MDES日均运行成本CMDES_avg和SESS 日均收益GSESS_avg，对应的约束条件包括等式约束以及不等式约束，见上节。

1.走出课堂，走向社会。大学生创业要脚踏实地，立足实践。对于在学校书本上所学到的知识，要充分发挥到实践当中去，不能闭门造车，做井底之蛙。创业要立足于社会，要敢于暴露自己的弱点，走向社会，付出行动才能发现别人的优点，取长补短。避免盲目自大，只学习书本知识而忽略技术本身。只有真正迈出脚步，虚心请教，敢于直面困难，吸取他人经验，才会成为一个成功的创业者。

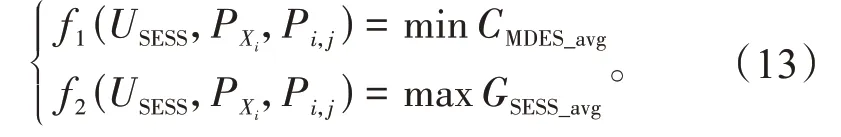
本文采用主目标函数法（ε约束法）将上述多目标问题转化为单目标问题。

主目标函数法是通过设置一个优化目标为主目标函数，把其他约束目标转化为约束，从而将多目标优化转变为可解的单目标优化。本文进行双目标优化时将CMDES_avg作为主目标，对GSESS_avg添加约束，求解CMDES_avg-GSESS_avg的Pareto前沿曲线，进而通过设置不同的约束实现Pareto 曲线求解，其数学表达为

式中：f1（x）为主要优化目标（CMDES_avg）；hu（x）为原约束；v为约束个数；f2（x）为转化为约束的目标（GSESS_avg）；ε2为需满足的约束。

通常将f2（x）划分为n个等间距的点并逐个作为约束

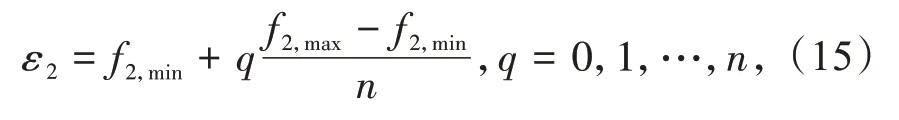
式中：f2，min，f2，max分别为f2（x）的最大值和最小值。

2.2 纳什议价

在以能源互联网络运行总成本最低为优化目标时，获得的最优解可能存在个别MDES 在参与共享储能后成本降低较少或成本持平的情况。为提高各MDES 参与的积极性，需要对其成本进行合理配置。本文采用纳什议价方法［18］对各MDES间的成本进行分配，具体流程为：以各MDES无共享储能下的单日运行成本作为纳什议价的谈判崩裂点，即所有MDES 所能接受的运行成本最大值；经过谈判各方的讨价还价，以各MDES 谈判后的运行成本与不参与共享储能时运行成本之差的乘积最大为目标，得到所有MDES 共同接受的运行成本，即为纳什谈判解。该方法能同时满足对称性、Pareto 最优、独立与无关选择以及线性变换不变性4 个性质，具体表达式为

考虑到式（16）为非凸非线性问题，利用文献［19］的方法将其分解为2 个凸的子问题，采用IPOPT求解器求解，所分解的子问题依次为

2.3 求解流程

在Matlab 软件中使用YALMIP 环境进行建模并利用Cplex 求解器进行求解。多目标优化求解流程如图3所示。

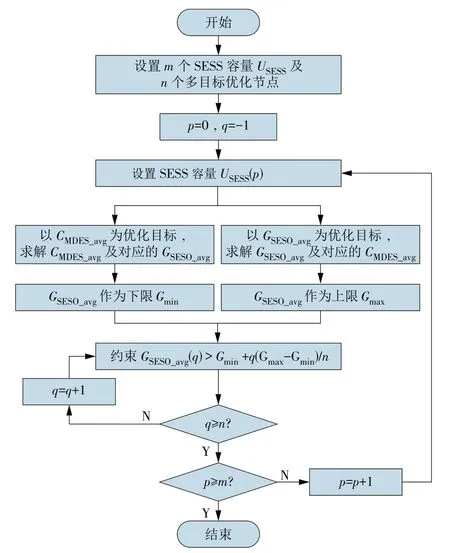
图3 多目标优化求解流程Fig.3 Solving process of multi-objective optimization

首先设置m个SESS 容量以及n个多目标优化节点，在某一容量下分别以GSESS_avg为单目标和以CMDES_avg为单目标进行优化，在得出GSESS_avg的最大、最小值后，将收益的取值区间分成n等份进行以CMDES_avg为目标的单目标优化；将m个SESS 容量进行遍历得到Pareto 前沿曲线后，选取合适的SESS 容量并通过模糊隶属度法求解Pareto最优解。

3 共享储能对MDES的影响

前述共享储能能源互联网络涉及的4 个MDES的冷热电负荷需求如图4—5 所示。根据当地典型日光照、温度以及各能源系统建筑面积规划得出PV机组出力曲线（如图6 所示），电网商业用电价格及居民用电价格如图7 所示［20］。其中：冬季为12 月至次年2月，共90 d；过渡季为3月至5月，9月至次年1月，共183 d；夏季为6月至8月，共92 d。MDES参数见表2。

表2 MDES参数Table 2 Parameters of the MDES

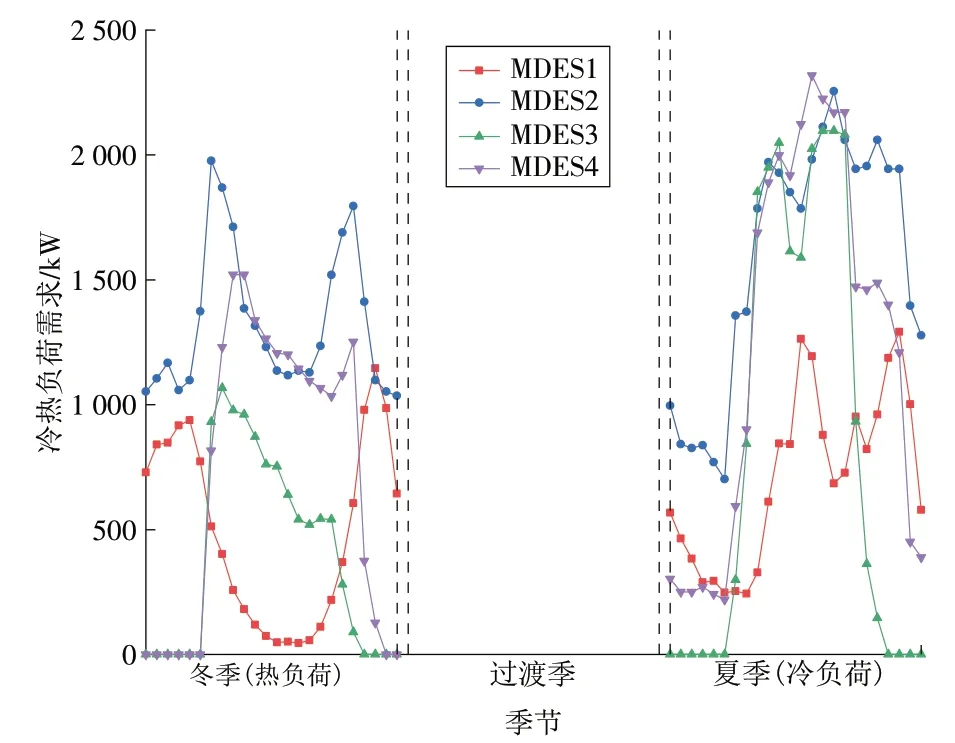
图4 各季节典型日冷热负荷需求Fig.4 Typical daily cooling and heating loads in different season

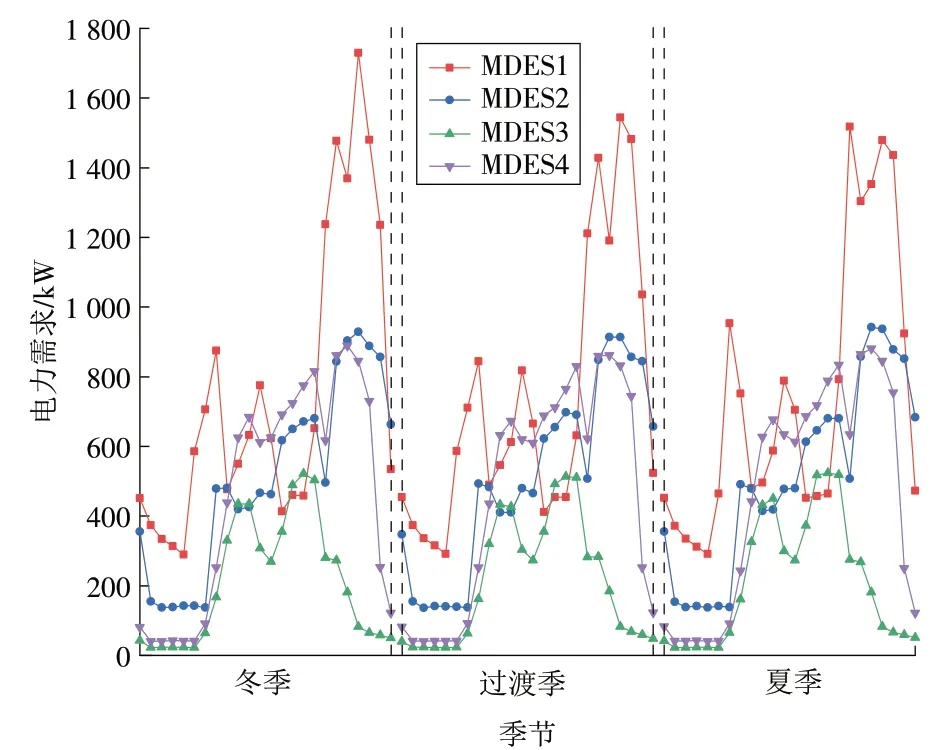
图5 各季节典型日电力需求Fig.5 Typical daily power load in different season

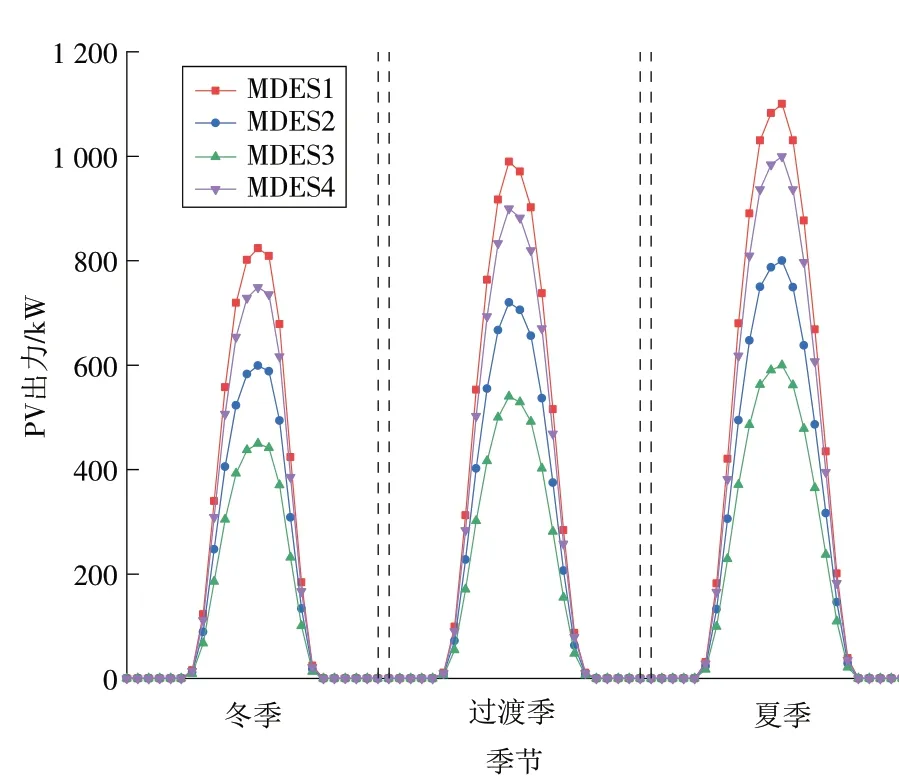
图6 各季节典型日PV出力Fig.6 Typical daily PV output in different season

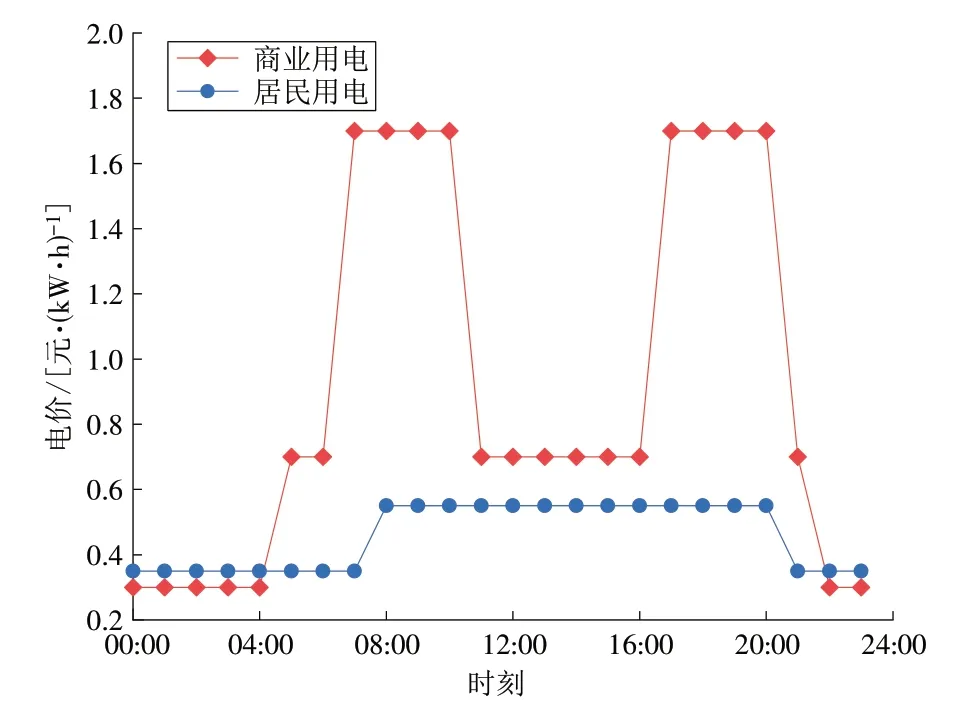
图7 电网商业用电价格及居民用电价格Fig.7 Prices of commercial electricity and residential electricity

此处容量规划是确定无共享储能设备时MDES的最优设备装机容量，为计及共享储能的MDES 优化打基础。MDES 全年总成本由年均建设、维护成本和全年运行成本构成，其中年均建设及维护成本由装机规模决定，全年运行成本为各季节单日运行成本乘以对应天数并求和。此处以MDES全年总成本为优化目标，求解出各MDES的最优装机规模（见表3），该模式下的最低总成本为25 826 元。

表3 MDES最优装机规模Table 3 Optimal installed capacity of the MDES kW·h

上述MDES引入共享储能后会带来运行成本的变化，为了进一步实现SESS 与能源互联网络的共赢，首先需要进行储能容量的敏感性分析。设置优化目标1 为CMDES_avg，优化目标2 为GSESS_avg，研究不同优化目标下SESS 容量变化对CMDES_avg以及GSESS_avg的影响，如图8所示。

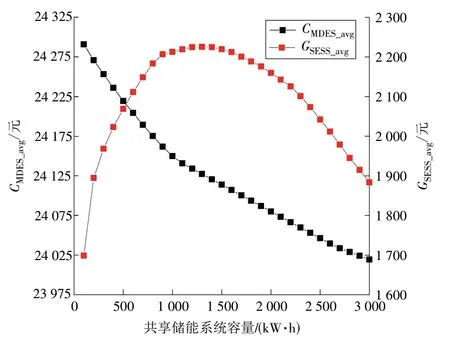
图8 不同优化目标下SESS收益及MDES成本Fig.8 Benefits obtained by the SESS and costs of the MDES under different optimization goals

由图8 可知，在以CMDES_avg为优化目标时，随着SESS 容量的上升，CMDES_avg不断降低，但由于边际效应CMDES_avg降低幅度逐渐减小。在以GSESS_avg为优化目标时，随着SESS 容量的上升，GSESS_avg呈现先上升后下降的趋势，这是由于CMDES_avg需要小于不引入共享储能时的成本，随着SESS 容量的增大，超过一定容量后MDES由于成本限制无法提供与容量上升相平衡的费用，故导致GSESS_avg下降。GSESS_avg与CMDES_avg是相悖的，需要对储能的容量及二者的收益和成本进行合理的规划。

为得到综合考虑GSESS_avg与CMDES_avg最优的共赢结果，通过主目标函数法对交互收费和交互不收费各微能源网之间进行纳什议价来求解CMDES_avg（p，q）-GSESS_avg（p，q）前沿曲线，如图9所示。

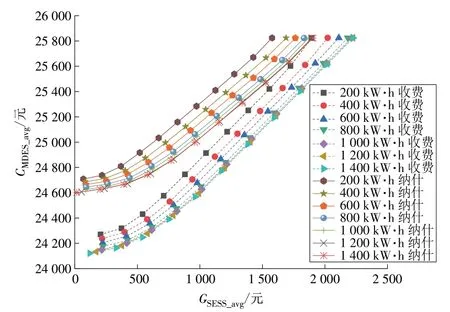
图9 交互收费和纳什议价模式的Pareto前沿曲线对比Fig.9 Pareto frontier curves in two-way charging mode and in Nash bargaining mode

由图9 可以看出，随着SESS 容量的增加，在交互收费模式和纳什议价模式下得到的Pareto 前沿曲线均向最优解靠近，且靠近的趋势随容量的增大而减缓。纳什议价模式下SESS 容量为200 kW·h 时，优化目标为CMDES_avg的结果为24 709 元，优化目标为GSESS_avg的结果为1 578 元；SESS容量为600 kW·h时，优化目标为CMDES_avg的结果为24 664 元，优化目标为GSESS_avg的结果为1 764 元，均优于SESS 容量为200 kW·h 时的结果。但随着SESS 容量的增加，优化效果逐渐减弱，如SESS 容量增加至1 000 kW·h 时，优化目标为CMDES_avg的结果为24 624 元，优化目标为GSESS_avg的结果为1 870 元。各微能源网之间进行交互收费与纳什议价时Pareto 前沿曲线随储能容量变化的趋势相同，但由于进行了多个主体间的利益均衡，能量交互时限制条件增加，导致Pareto 前沿曲线相比交互收费模式向理论最劣点移动。在SESS 容量上升至1 000 kW·h 后，各自的Pareto 曲线近似重合，出于设备投资回收周期的考虑，在SESS 容量为1 000 kW·h 的Pareto 曲线上确定Pareto 最优推荐解。

由于不同目标函数的尺度不同，难以直接从Pareto 前沿获得表征实际目标与最优化目标偏差值的最优解。模糊隶属度方法可以表征实际目标与最优目标的偏差程度，在此通过线性的方法计算目标函数的隶属度。在SESS 容量为1 000 kW·h 的情况下，2 种模式的隶属度曲线如图10 所示。通过仿真计算可得：在交互收费模式下，推荐最优解为CMDES_avg为24 825 元，GSESS_avg为1 214 元；在纳什议价模式下推荐最优解为CMDES_avg为25 043 元，GSESS_avg为977 元。2 种模式下MDES 的成本与无共享储能相比均下降。

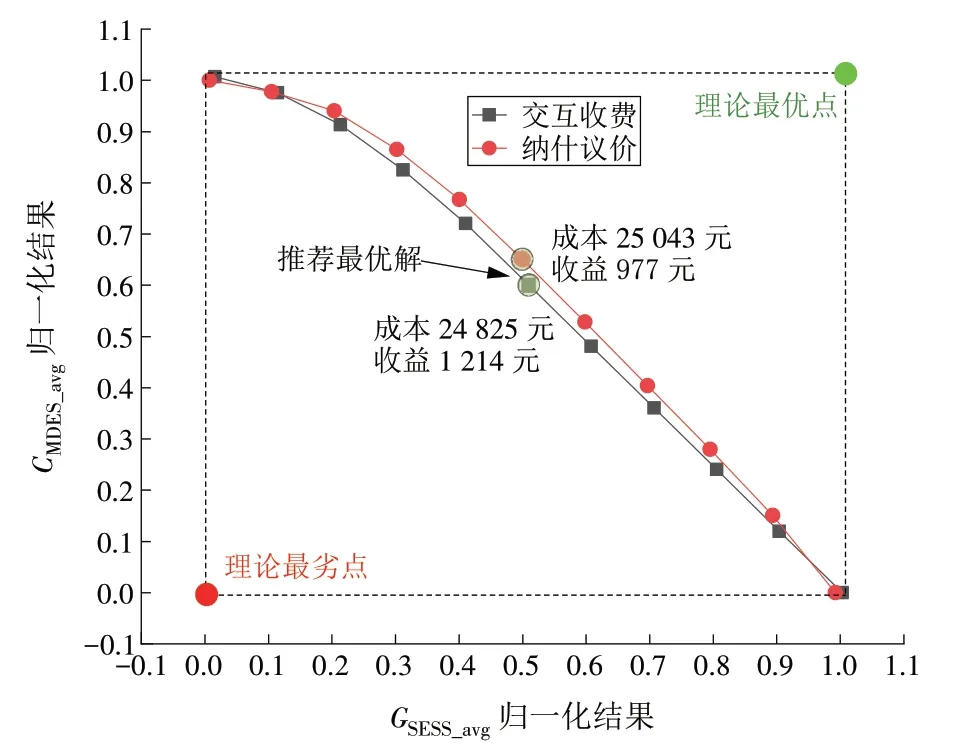
图10 2种模式下的归一化曲线Fig.10 Normalized curve in two modes

由图11—12可以看出，在加入各系统之间运行成本的纳什议价后，单一能源系统交互的输入输出能量差值减小，MDES 通过共享储能获得的效益更加均衡，提高了其参与共享储能的积极性。MDES与SESS的交互电能如图13所示。

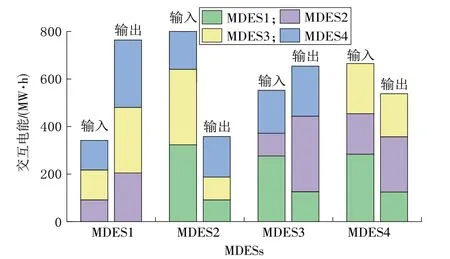
图11 交互收费模式下各系统交互电能Fig.11 Electric energy interaction between different systems in two-way charging mode

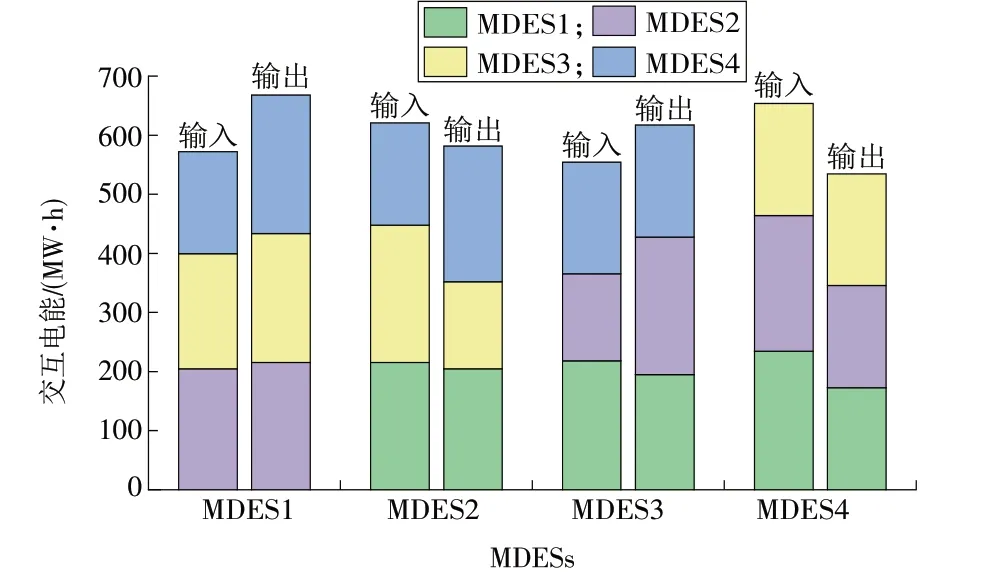
图12 纳什议价模式下各系统交互电能Fig.12 Electric power interaction between different systems in Nash bargaining mode

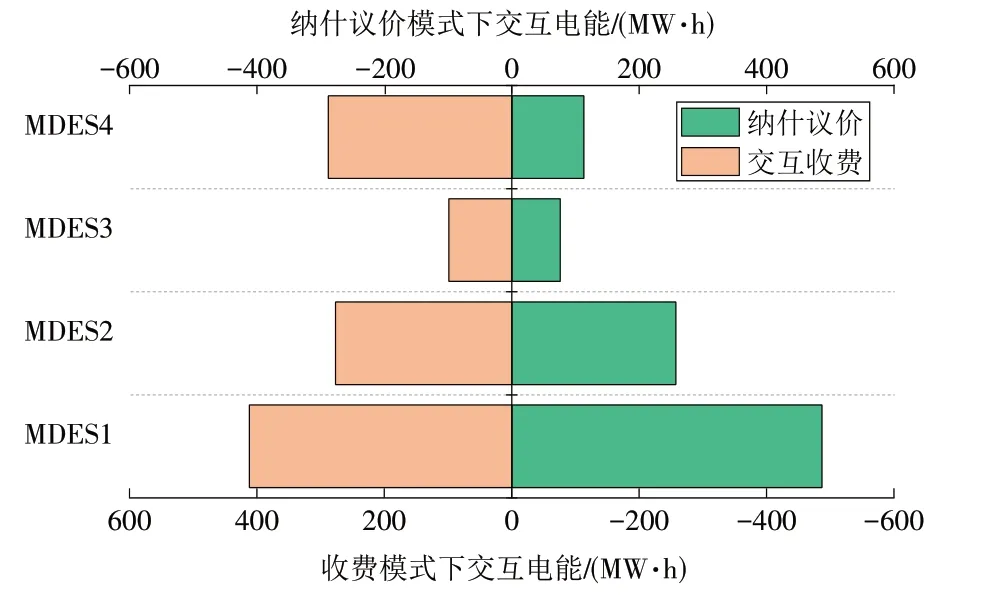
图13 2种模式下MDES与SESS的交互电能Fig.13 Electric power interaction between the MDES and the SESS in two modes

4 结论

本文提出了在考虑公平性下共享储能参与的能源互联网络的双目标规划及优化方法，通过所建立的1 个SESS 和4 个MDES 的算例进行验证。主要结论如下。

（1）随着SESS 容量的增加，CMDES_avg-GSESS_avg的Pareto 前沿曲线更优。在本文的算例下，SESS 容量超过1 000 kW·h时，随着容量的增大，Pareto 前沿曲线变优效果迅速减弱。

（2）加入共享储能后，4 个MDES 的总体成本降低。加入纳什议价对成本进行分配后，MDES 的总成本升高，但4 个MDES 间的利益分配更加公平，提高了能源系统参与共享储能的积极性。