基于散布熵的往复压缩机气阀故障特征提取方法

赵海峰，张家骏，吕建卓

（东北石油大学 机械科学与工程学院，黑龙江大庆 163318）

0 引言

往复压缩机是炼油、化工等流程工业中广泛应用的过程流体机械，而气阀是往复压缩机故障率最高的部件［1］，其工作状态正常与否直接影响压缩机的排气量、功率损耗及运转的可靠性［2］。近年来，国内外学者为保障气阀可靠性运行在模型仿真［3-4］、故障特征提取与诊断［5-6］等方面开展了大量研究工作，取得了较好效果。但由于往复压缩机结构复杂、激励源众多，导致气阀振动信号具有明显的非线性、非平稳、强冲击等特点，传统的基于线性、平稳信号的处理方法难以有效提取故障特征。而近似熵、样本熵、排列熵等基于熵的非线性特征提取方法，因其分类精度高、抗噪能力强、不依赖于先验知识等优点，在机械故障诊断中得到广泛研究［7-11］。但是，近似熵和样本熵计算速度慢，实时性差，且受突变信号影响大，排列熵虽然计算速度快，但未能考虑振幅值之间的差异［12-13］，均难以满足状态监测及故障诊断所需实时性、鲁棒性及准确性的特征提取要求。基于此，ROSTAGHI 等［14］于2016 年提出了散布熵。该算法克服了近似熵、样本熵与排列熵的部分缺陷，具有计算速度快、受突变信号影响较小等优点，在滚动轴承、齿轮箱等旋转机械特征提取及故障诊断中得到较好应用，但在往复机械中研究较少［15-20］。

鉴于散布熵在旋转机械特征提取及故障诊断应用中的良好效果，本文将其引入往复压缩机故障诊断领域，并以2D12 型往复压缩机气阀正常、阀片断裂与弹簧失效3 种状态的实测振动加速度信号为研究对象，进行基于散布熵的故障特征提取研究，从鲁棒性、稳定性方面验证散布熵在往复压缩机气阀故障特征提取的适用性。

（5）对于cm种散布模式πvvvm01...1-，每种散布模式的概率如下：

（6）最后根据香农熵的定义，计算散布熵（DisPEn）的值如下：

1 散布熵算法

散布熵是一种用于评估非线性时间序列不规则性、复杂性的方法。计算一个长度为N 的时间序列x={x1，x2，x3，…，xN}的散布熵，算法如下［14］：

（1）首先，采用正态分布函数：

将非线性时间序列x 映射到y={y1，y2，y3，…，yN}，y（0，1）。式中，σ和 μ 分别表示为标准差和均值。

（2）采用式（2）所示线性变换式将每个yj赋值给［1，2，…，c］的整数，即：

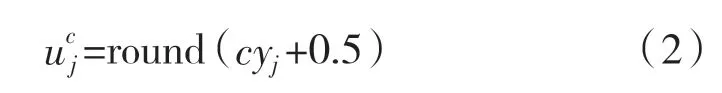
round——取整函数；

c ——类别个数。

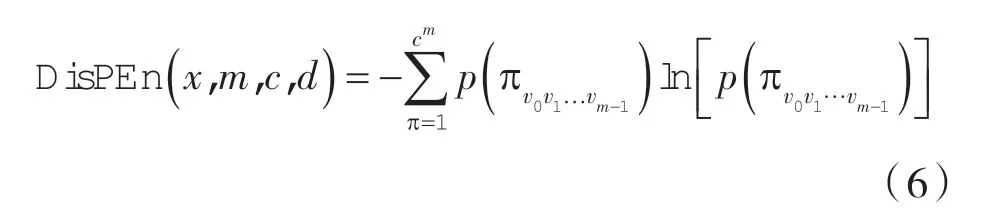
由式（6）可知，与散布熵相关的主要参数为嵌入维数m、类数c和时延d，其相应取值会对散布熵计算结果产生一定影响。根据文献［12］的参数分析，选取m=2、c=8、d=1 作为该研究中的计算参数。

2 往复压缩机气阀故障实例分析

2.1 往复压缩机气阀振动测试

振动测试过程及数据与文献［21］中一致，即以大庆天然气分公司南区压气站2D12 型往复压缩机为试验对象，根据气阀常见故障，在二级盖侧吸气阀分别设置正常、阀片断裂与弹簧失效3 种状态，并进行振动测试。测试中，在该气阀阀盖上布置振动加速度传感器，采用键相器获取气阀振动整周期振动加速度数据，采集系统为INV306U-6660 智能数据采集处理分析仪与INV-1021 程控多功能信号调理仪，采样频率分别为20，50，70 kHz。从状态监测实时性及存储等方面考虑，取采样频率20 kHz 的数据进行分析，每个周期数据长度为2 412 点。

2.2 试验数据分析

往复压缩机信号以多源非线性冲击信号为主［22］，当发生故障时，振动信号波动变得更加复杂，难以像旋转机械那样采用仿真信号进行准确模拟，进而无法验证方法有效性。因此，该项研究以实测气阀振动信号为研究对象，进行散布熵方法的适用性分析。

2.2.1 散布熵鲁棒性分析（1）50 Hz 工频干扰分析。

机械振动信号在采集、转换以及传输的过程中可能会存在50 Hz 工频干扰，从而可能对设备运行状态判断及故障诊断准确性产生影响［23］，尤其是对以状态监测为目的的特征参数影响更大。图1 示出气阀阀片断裂故障时的振动加速度时域波形，图2 示出了其频谱。

图1 阀片断裂振动信号时域波形Fig.1 Vibration signal time domain waveform of valve plate fracture

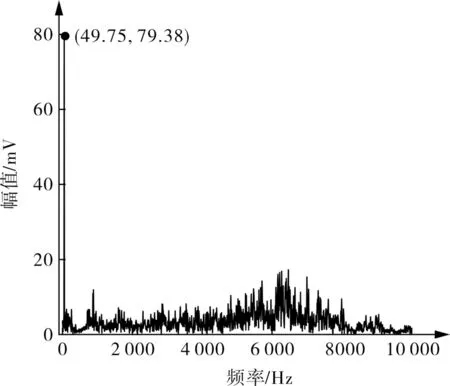
图2 阀片断裂振动信号频谱Fig.2 Vibration frequency spectrum of valve plate fracture

由图1 可知，所测试振动加速度时域波形图中含有明显的周期信号，经频谱分析可知，该周期信号频率为50 Hz（图2 所示为49.75 Hz，主要受频率分辨率影响），且幅值很大，表明测试振动信号受到较严重的工频干扰。

为了分析该干扰是否影响散布熵的特征提取能力，以20 组整周期阀片断裂振动信号为对象，并分别计算采用陷波器消除50 Hz 工频干扰前后的信号散布熵，采用箱线图对比其差异，如图3 所示。其中方框的上中下3 个横线，分别是数据的上四分位数，中分位数和下四分位数，意味着方框包含了大多数的数据。因此，方框的宽度在一定程度上反映了数据的波动程度。同时方框的上方和下方又有两条直线，表示数据集的最大值和最小值。

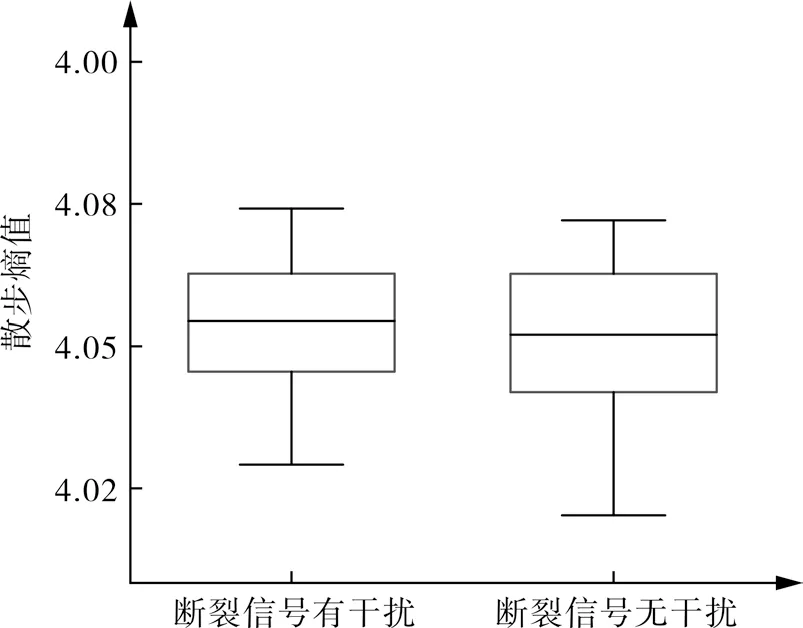
图3 阀片断裂信号干扰前后散布熵箱线Fig.3 Box plot of dispersion entropy before and after power frequency interference of valve plate fracture

由图3 可知，对于50 Hz 工频干扰前后的吸气阀阀片断裂振动信号，其散布熵值的箱线图基本一致，误差变化较小，表明该方法具有克服50 Hz 工频干扰的能力，鲁棒性较好。

（2）不同信噪比分析。

为验证散布熵方法的抗噪能力，以吸气阀正常时整周期振动信号为原信号，通过加入不同信噪比的高斯白噪声，分别计算散布熵与样本熵［24］（其中，m=2，r=0.15×信号标准差），并进行对比。表1 和图4 分别示出散布熵与样本熵随不同信噪比合成信号的熵值及变化率曲线。由表1 中可知，散布熵及样本熵值从信噪比50 dB 开始总体上均随吸气阀正常信号信噪比的降低而增大，而在该信噪比之上时两者均保持不变。由图4 可知，散布熵在信噪比20 dB 以下时开始出现曲线变化，但变化率均在5%以内；样本熵则在信噪比50 dB以下时出现曲线变化，并且随信噪比的继续降低，变化率逐渐增大，当信噪比为0 时，变化率达到34%。由此表明，与样本熵相比，散布熵在分析含高斯白噪声的往复压缩机气阀非线性、强非平稳振动信号时，对噪声鲁棒性较高，表现出了更优的抗噪能力。

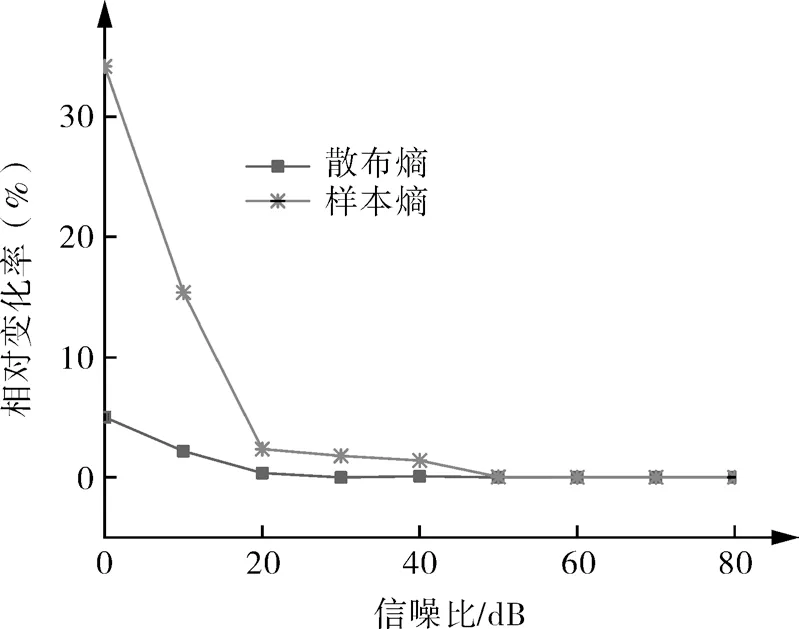
图4 熵值-噪声变化率曲线Fig.4 Curves of change rate between entropy and SNR

表1 不同信噪比熵值Tab.1 Entropy values of different SNR

2.2.2 散布熵稳定性分析

对于采集的往复压缩机振动信号而言，时间序列是非平稳的，可考虑采用序列的变异性大小作为衡量信号稳定性的统计特征，其变异性大小可用变异系数（Coefficient of Variation，简称CV值）来表示，计算公式如下［25］：

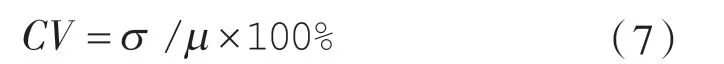
式中 σ ——标准差；

μ ——均值。

首先分别计算吸气阀正常、阀片断裂和弹簧失效3 种状态各20 组整周期振动加速度信号的散布熵值和样本熵值，然后采用式（7）计算相应CV 值，结果见表2。

表2 吸气阀3 种状态的标准差、平均值和CV 值Tab.2 Standard deviation, mean value and CV value of suction valve in three states

由该表可知，气阀3 种状态的散布熵变异系数均很小，且低于1%，而与之相比，样本熵的变异系数则较大，尤其是阀片断裂状态的变异系数达到5.2%。由此表明，散布熵在分析往复压缩机不同状态气阀振动信号的稳定性更佳，且优于样本熵。

2.2.3 散布熵特征提取分析

由前述研究可知，散布熵具有较好的鲁棒性和稳定性，为与样本熵分析结果进行对比，验证散布熵在往复压缩机气阀状态特征提取的有效性，仍采用前述2D12 型往复压缩机二级盖侧吸气阀正常、阀片断裂及弹簧失效3 种状态的各20 组振动加速度信号进行分析。

图5，6 分别示出气阀3 种状态的散布熵曲线与样本熵曲线。由图可知，气阀正常时的散布熵值与样本熵值均与阀片断裂及弹簧失效2 种故障状态的熵值区分明显，且均小于故障状态的熵值，表明气阀故障时的振动加速度信号更加复杂。但由图5 可知，阀片断裂与弹簧失效2 种故障状态的散布熵值几乎没有交叉，而与之相比，图6 示出该2 种气阀故障状态的的样本熵值存在明显交叉，不能有效区分。

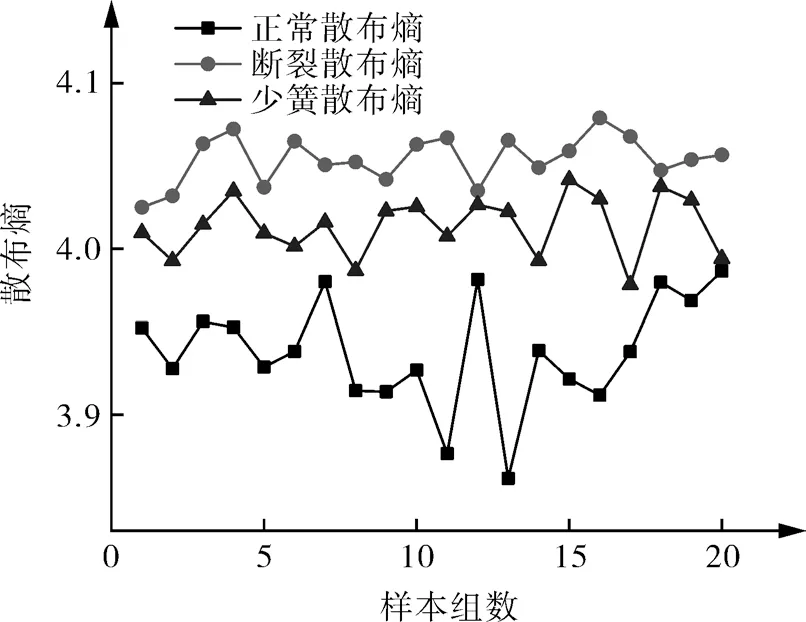
图5 3 种状态散布熵曲线Fig.5 Dispersion entropy curves of three states

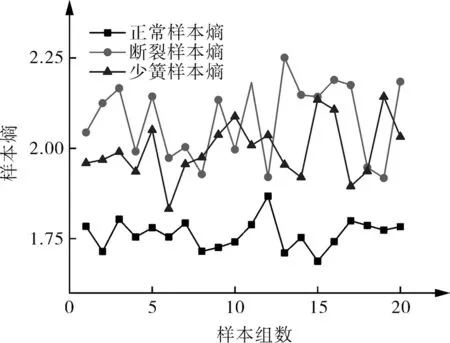
图6 3 种状态样本熵曲线Fig.6 Sample entropy curves of three states

3 结论

（1）气阀振动测试信号中是否存在工频干扰对散布熵影响很小，表明散布熵具有较强的抗工频干扰能力。

（2）与样本熵相比，散布熵在信噪比20 dB 时才发生变化，并且0 dB 时达到最大，但最大变化率不超过5%；而样本熵则在50 dB 时即发生变化，0 dB 时达到最大，最大变化率为34%，表明散布熵具有更佳的抗噪能力。

（3）气阀正常、阀片断裂及弹簧失效3 种状态的散布熵变异系数均低于1%，明显优于样本熵（阀片断裂时变异系数5.2%），表明散布熵具有更佳的稳定性。

（4）提出的基于散布熵的特征参数提取方法，与样本熵相比，可以有效区分气阀正常、阀片断裂及弹簧失效3 种状态，为往复压缩机气阀状态监测及故障诊断提供了一个有效特征。