Python语言在轮胎带束层后处理分析中的应用

任 帅，张永峰，张梦洁，张伟伟

[浦林成山（青岛）工业研究设计有限公司，山东 青岛 266042]

进入21世纪，轮胎行业中有限元仿真方法的应用越来越广泛，已经成为轮胎研究中必不可少的工具[1-5]。带束层作为轮胎的重要骨架结构，也是主要仿真目标之一，而带束层的仿真研究也大量开展。危银涛等[6]通过试验验证带束层帘线张力仿真的准确性，魏领军等[7]研究了径向负荷下的带束层张力的变化，孙鹏飞等[8]研究了侧向力对带束层张力的影响。但大部分带束层仿真研究存在带束层数据不能有效利用的情况，仅关注轮胎接地印痕中心横截面上的张力，不能全面地描述带束层受力。

为了提高数据使用率，全面分析带束层受力情况，本工作通过Python脚本提取Abaqus结果的张力数据，利用Pandas，Numpy和Matplotlib等Python库对数据进行传递、处理和显示，对带束层张力进行多维度分析。

1 分析工具和流程

1.1 工具简介

Python是一种面向对象的编程语言，与有限元仿真软件Abaqus兼容性好，拥有大量数据处理库，在数据分析领域有较高的使用率。

Numpy（Numerical Python）是Python语言的一个扩展程序库，支持大量的维度数组与矩阵运算，针对数组运算提供大量的数学函数库。

Pandas适用于数据操纵和分析，建立在Numpy之上，允许为行和列设定标签，能够将不同的数据集合在一起，方便提取Excel数据。

Matplotlib是Python的数据可视化工具库，与Numpy等数据处理平台联合使用，可非常方便地可视化处理数据，同时依托Python编程，可灵活调整数据显示。

1.2 后处理流程

后处理流程如下：模型导入→数据输出→Pandas数据提取→Numpy数据处理→Matplotlib可视化输出。

Abaqus脚本读取odb文件的分析结果和inp文件中帘线节点路径数据，从横截面和纵截面两个方向输出接触区域的帘线张力，建立x和y方向的网状数据集，输出形成Excel文件。

通过Pandas库解析Excel文件，使用Numpy数据引入程序并转化为array格式后进行数据处理。

使用Matplotlib库将已经处理好的数据进行3D可视化处理，对更关注的截面数据进行切片式2D图形显示。

2 模型建立与数据分析

2.1 有限元模型建立

以295/80R22.5载重子午线轮胎为例，采用标准轮辋，在标准充气压力为930 kPa、单胎额定负荷为3 550 kg下，建立轮胎2D和3D有限元模型，见图1。

图1 轮胎有限元模型

2.2 负荷下的带束层张力分析

以接地印痕中心线为x轴，接地印痕长轴方向为y轴，受负荷区域带束层帘线作为分析对象，将Abaqus输出数据通过Pandas和Numpy处理传递，使用Matplotlib显示带束层张力。轮胎充气及加载后的带束层张力有限元分析结果见图2。

图2 轮胎加载及充气后带束层张力有限元分析结果

结合Numpy数据切面功能，可以显示不同横截面上张力的变化情况，结果如图3所示。

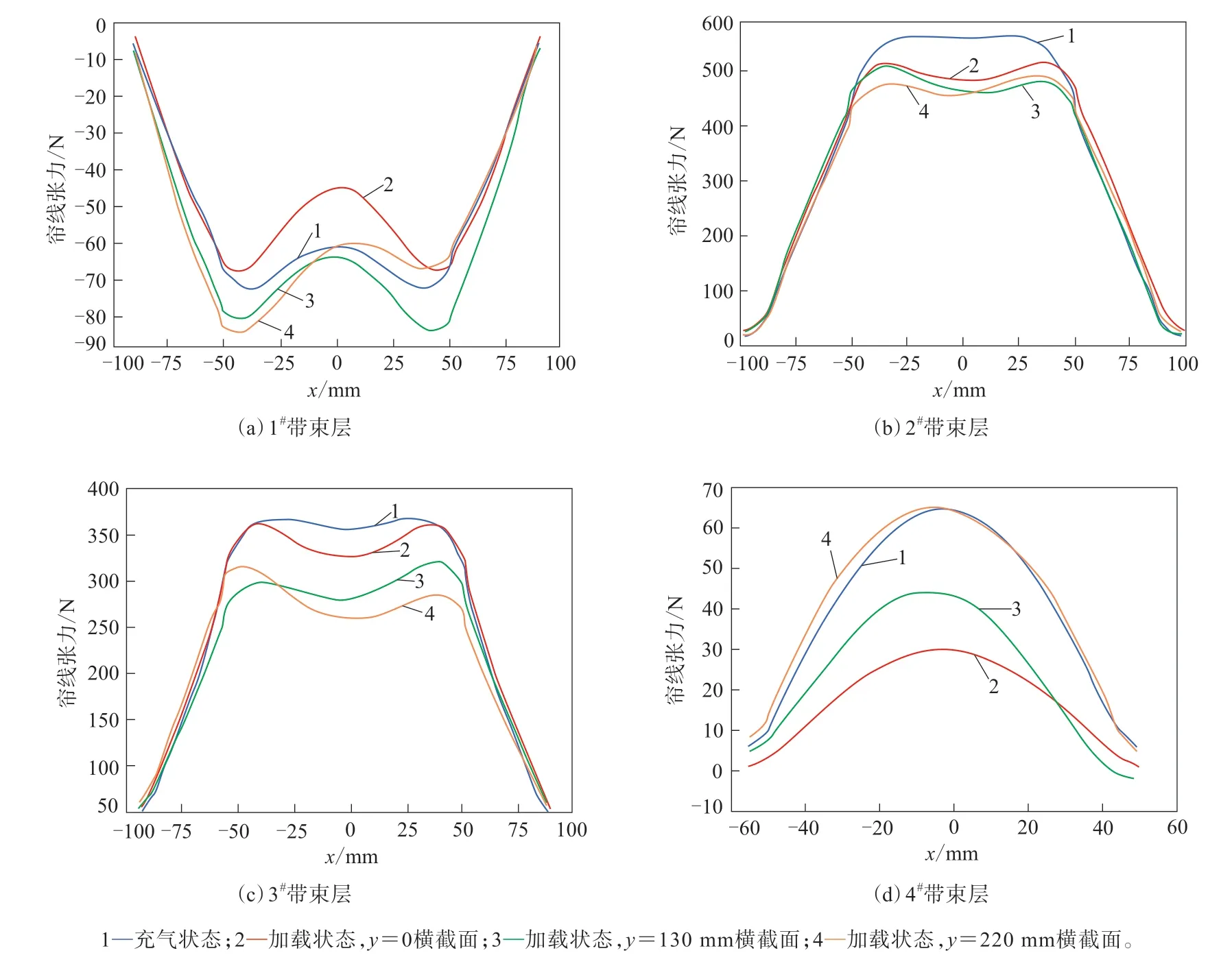
图3 不同横截面带束层张力

由图2和3可见：1#带束层加载后接地印痕中心线横截面上，胎冠中心附近帘线张力明显高于充气状态，远离接地印痕中心线的横截面上的帘线张力低于充气状态；2#带束层加载后胎冠中心附近帘线张力较充气状态下降较多，且区域内张力沿y方向变化较小，负荷较为均匀地作用于各个横截面上；3#带束层加载后胎冠中心张力较充气状态下降较多，远离接地印痕中心线截面张力下降较大，沿y轴呈现中凸外凹的形状；4#带束层加载后在中心横截面上张力较充气状态下降较大，距离接地印痕中心线越远的截面上张力越接近充气状态。

全钢载重子午线轮胎在加载后其带束层帘线张力变化非常复杂，仅仅对接触中心横截面处的张力进行分析，无法全面地体现轮胎带束层帘线受力，而使用本方法可以较为清晰全面地显示帘线张力空间分布情况。

2.3 帘线受力分析

通过收集的张力数据，可以反推得到帘线各部分的受力情况及与帘线接触的胶料受力情况。

在帘线a与b两点之间的张力差[9]（Δf）为帘线与胶料截面沿帘线方向的剪切力从a到b的积分，如下式：

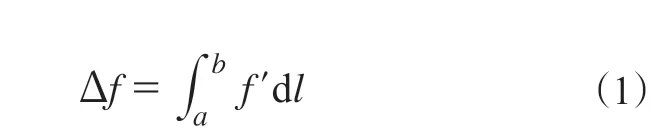
拓展到二维带束层上为

式中，f′为帘线单位长度（l）上所受的帘线方向上的剪切力（帘线张力方向的受力），Δfx和Δfy为x和y方向上的张力差，F为区域内的帘线张力方向受力的总和，Δfx/x和Δfy/y为帘线在x和y方向上的张力梯度。

以2#带束层为例，使用Matplotlib分析负荷下帘线的受力情况，结果如图4所示。

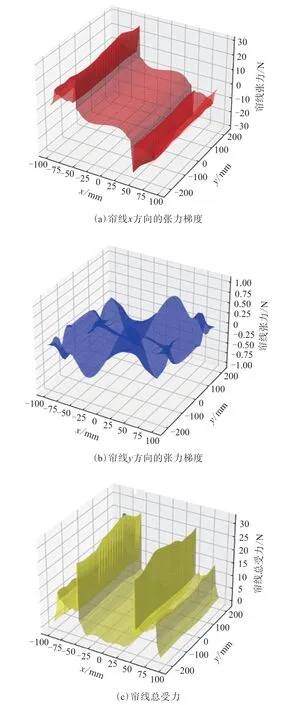
图4 2#带束层受力分析

由图4可见，带束层的x方向张力梯度远大于y方向的张力梯度，胎肩处带束层受力出现峰值，此位置处于2#带束层的边缘位置，由于力学性能产生较大变化，故此位置上2#带束层受力最大，使用Numpy的矩阵最大值函数和Matplotlib的散点函数可以非常方便地捕捉并显示帘线受力最大位置以及帘线受力的最大值，这对设计阶段多方案选择和改进具有参考意义。

3 部分重要程序代码[10]

3.1 负荷区域上的张力提取

u=range（600000，800000，10000）+range（0，210000，10000）#3D旋转模型接触区域#节点基数集合

xianshi（path1，q）#xianshi函数为自定义函数，保存此路径的连线张力

3.2 使用Pandas库将Excel中的数据提取

3.3 3D图显示

ax=fig.add_subplot（111，projection='3D'）

surf=ax.plot_surface（X，Y，R，rstride=1，cstride=1，alpha=0.6，color='blue'，label='加载后连线张力'）#X，Y节坐标集合，R为张力集合

3.4 2D切片显示

plt.plot（X[20]，R[20]，label="加载后，接触面中心横截面"，color="yellow"）

3.5 带束层张力x方向的张力梯度

X1，X2=X.T[：-1]，X.T[1：]

X3=X2-X1

X4=X1.T

R1，R2=R.T[：-1]，R.T[1：]

R3=R2-R1·

RNEW=R3.T/X3.T

Y1=Y.T[：-1].T

surf=ax.plot_surface（X4，Y1，RNEW，rstride=1，cstride=1，alpha=0.6，color='red'，label="2#带束层方向张力梯度"）

4 结论

利用Python的Matplotlib，Pandas和Numpy等数据分析和可视化工具，对带束层张力进行3D可视化和力学分析。结果显示，本方法对径向负荷下的带束层受力变化情况分析较为全面，具有可行性和扩展性。通过此方法可以有效提高带束层仿真数据的利用率，增加仿真在产品设计和改进中的参考依据，更可以利用既有代码挖掘带束层数据更多的应用场景。