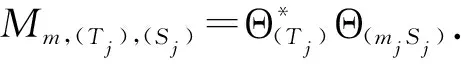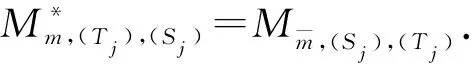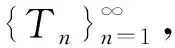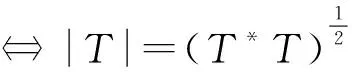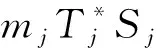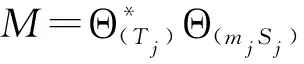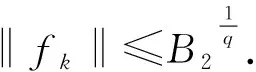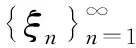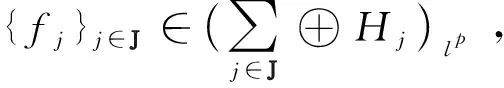Hilbert空间上的算子值 (p,q)-Bessel乘子*
孙 悦, 李鹏同
(南京航空航天大学理学院,210016,江苏省南京市)
0 引 言
1952年,Duffin和Schaeffer[1]在研究非调和Fourier分析时,进一步发展了Gabor 分解信号的方法,提出了Hilbert空间中框架的概念. 特别是受Daubechies等人在1986年的工作[2]的刺激,人们对框架理论及其应用进行了深入研究,产生了一系列重要研究成果.
设H是Hilbert空间,{fj}j∈是H中的序列,是有限或可数指标集. 如果存在常数A,B>0,使得
(1)
则称{fj}j∈是H中的框架,常数A,B分别称为该框架的下界和上界. 如果A=B(=1),则称 {fj}j∈是紧框架(Parseval 框架). 在(1)式中如果只要求右不等式成立,则称{fj}j∈是 Bessel 序列. 关于框架理论的详细知识,可参阅文献[8,10].
框架作为Hilbert空间中Riesz基的推广,具有许多优于Riesz基的优良性质,在传感器、 信号和图像处理、 编码与传输以及无线电通信等领域中一直是一个研究重点. 信号表示在数字信号处理中起着基础性的作用,而表示的有效性可决定信号压缩、去噪和特征提取等相关算法的性能.因为框架有不同于基的冗余性,所以它可以为不同空间中的元素生成灵活的表示.此外,某些学科中的许多对象都可以被描述为框架乘子,例如,信号处理中的时变滤波器和听觉场景分析中的时频滤波器. Balazs 在文献[3]中首次提出了Hilbert空间中的Bessel乘子的概念.
设H1,H2是两个Hilbert空间,{gj}j∈⊆H1,{fj}j∈⊆H2是Bessel 序列,数列m={mj}j∈∈l∞. 称算子
是关于Bessel序列{fj}j∈,{gj}j∈的Bessel乘子,并称数列m为该乘子的符号. 如果 {fj}j∈,{gj}j∈是框架或Riesz序列,则称相应的乘子为框架乘子或Riesz乘子.
随着框架理论研究的不断深入以及应用的需要,出现了框架的各种推广形式. Gasazza在文献[6]中提出了子空间框架的概念,之后又与Kutyniok 和Li合作在文献[7]中 对这类新框架作了进一步研究,并将其重新命名为融合框架. 融合框架在信号传输的分布式处理中具有重要的应用,它是通过加权分布式处理将Hilbert 空间上所有子空间的信号融合到了一起,比较有效地解决了因框架系统太大而难以有效处理相关数据的问题,这也将Hilbert空间中满足框架条件的“向量列”推广到了满足一定条件的“子空间列”. 受此启发,很多学者开始研究满足一定条件的“算子列”. 2006年,Sun 在文献[13,14]中提出了g-框架的概念,并刻画了这类框架的若干性质.g-框架涵盖了框架的很多推广形式,融合框架就是一种特殊的g-框架. 在此基础上,Kaftal,Larson和Zhang在文献[9]中引入了算子值框架的概念,着重从算子理论与算子代数的角度对它进行了深入研究.
设H和H0是Hilbert 空间,{Aj}j∈⊆B(H,H0). 称{Aj}j∈是H上的算子值框架,如果存在常数0 (2) a,b分别称为该框架的下界和上界. 如果a=b,则称{Aj}j∈是算子值紧框架;如果a=b=1,则称{Aj}j∈是算子值Parseval框架;如果(2)右边不等式成立,则称{Aj}j∈是算子值Bessel序列. 受上述这些工作的启发,本文将在Hilbert空间上 引入算子值p-框架、算子值p-Riesz基和算子值(p,q)-Bessel乘子等概念,重点对乘子进行研究. 我们将会看到一个算子值 (p,q)-Bessel乘子是一个有界线性算子,它是由一个算子值p-Bessel序列、一个算子值q-Bessel序列和一个有界数列构成. 主要结果体现在3个方面:一是在一定条件下,证明了当有界数列分别属于c0、l1和l2时,相应的乘子分别是紧算子、迹类算子和Hilbert-Schmidt算子 (定理7);二是当构成乘子的算子值q-Bessel序列换成p-Riesz基时,有界数列与乘子之间的对应是一对一的(定理9);三是在某种意义下,证明了乘子关于其构成元素具有连续依赖性(定理10). 本节最后固定几个本文中使用的记号. 设H,K是Hilbert空间.IH或I表示H上的恒等算子,B(H,K)表示从H到K上的全体有界线性算子,并记B(H):=B(H,H). 对于向量f∈H,g∈K,用g⊗f表示H到K的秩一算子:x|→(x,f)g,x∈H. 若无特别说明,表示某个有限或可数指标集,H和Hj(j∈)是可分的Hilbert空间,常数1 首先给出算子值p-框架等概念. 定义1设Tj∈B(H,Hj),j∈,1 (3) 则称{Tj}j∈是H关于{Hj}j∈的算子值p-框架,常数A,B分别称为框架的下界和上界. 如果A=B,则称{Tj}j∈是算子值紧p-框架;如果A=B=1,则称{Tj}j∈是算子值p-Parseval框架;如果(3)式只有右边不等式成立,则称{Tj}j∈是算子值p-Bessel序列. 对任一如上定义的算子值p-Bessel序列{Tj}j∈,总可定义如下的有界线性算子 称Θ(Tj)是{Tj}j∈的分析算子. 利用Hölder 不等式,不难证明收敛,进而得到 Θ(Tj)的伴随算子具有形式 又设Sj∈B(H,Hj)使得{Sj}j∈是算子值q-框架,如果则称{Tj}j∈是{Sj}j∈的对偶框架. 容易知道,当且仅当这表示如果{Tj}j∈是{Sj}j∈的对偶框架,那么{Sj}j∈也是{Tj}j∈的对偶框架. 此时,有重构公式 根据定义,下面的结论是明显的. 引理2 设Tj∈B(H,Hj),j∈. 如果{Tj}j∈是界为B的算子值p-Bessel序列,那么. 引理3 设Tj,Sj∈B(H,Hj),{Tj}j∈是算子值p-Bessel序列,{Sj}j∈是算子值q-Bessel序列,界分别是B1,B2,m={mj}j∈∈l∞,则算子 是良定义的. 证明不妨设是自然数集. ∀f,g∈H,根据Hölder 不等式,有 定义4称引理3中的算子M=Mm,(Tj),(Sj)是关于序列{Tj}j∈,{Sj}j∈的算子值(p,q)-Bessel乘子,m是该乘子的符号. 如果{Tj}j∈是算子值p-框架,{Sj}j∈是算子值q- 框架,则称M是算子值(p,q)-框架乘子. 命题5 设Tj,Sj∈B(H,Hj),{Tj}j∈是算子值p-Bessel序列,{Sj}j∈是算子值q-Bessel序列,界分别是B1,B2,m={mj}j∈∈l∞,则 (ⅰ) {mjTj}j∈是算子值p-Bessel序列且界为 证明(ⅰ) ∀f∈H, 进而结论成立. (ⅱ) ∀f,g∈H,根据Hölder 不等式和引理3, (ⅲ) ∀f,g∈H, 设T∈B(H),{ej}j∈是H的标准正交基,称T是正算子,如果(Tx,x)≥0,∀x∈H. 称T是Hilbert-Schmidt算子,如果此时称 为算子T的Hilbert-Schmidt范数. 称T是迹类算子,如果存在Hilbert-Schmidt算子A,B使得T=AB;此时称 为T的迹. 下面的引理描述了几个基本的事实. 引理6设T∈B(H),{ej}j∈是H的标准正交基,则 定理7 设 {dimHj}j∈∈l∞,m={mj}j∈∈l∞,Tj,Sj∈B(H,Hj),{Tj}j∈是算子值p-Bessel序列,{Sj}j∈是算子值q-Bessel序列,界分别是B1,B2,M=Mm,(Tj),(Sj),则 (ⅰ) 若m∈c0,则M是紧算子. 证明(ⅰ) 设m={mj}j∈∈c0,记mN:={Nj}j∈={m1,m2,…,mN,0,0,…),则∀ε>0,存在正整数Nε,当N>Nε时有‖m-mN‖∞<ε. 于是,∀f∈H,当N>Nε时,有 从而 ‖Θ(NjSj)-Θ(mjSj)‖→0(N→∞). 又因为 dimHj<∞(∀j∈),有 (ⅱ) 对每个j∈,因为Sj是有限秩算子,故可设其中yk∈H,fk∈Hj,Nj=rankSj. 结合Schmidt正交化过程,不妨设{yk是标准正交序列,则∀k,Sjyk=fk并且 设{ei}i∈是H的标准正交基. 由条件) 是正算子知M也是正算子,从而M=|M| 并且有 定义8设Tj∈B(H,Hj),j∈. 如果{Tj}j∈是完全的,即 {f∈H:Tjf=0,j∈}={0},并且存在常数0 则称{Tj}j∈是算子值p-Riesz基. 定理9设Tj,Sj∈B(H,Hj),m={mj}j∈∈l∞,{Tj}j∈是算子值p-Bessel序列且Tj≠0,∀j∈,{Sj}j∈是算子值p-Riesz基,则 (ⅰ) {Sj}j∈是算子值q-框架. (ⅱ) 映射m|→Mm,(Tj),(Sj)是单射. 证明(ⅰ) 由于{Sj}j∈是算子值p-Riesz基,故存在常数 0 (4) 设f∈H,fj∈Hj,⊆是有限子集,则 (5) 即 {Sj}j∈是算子值q-Bessel序列. 记{Sj}j∈的分析算子为Θ,则 当f∈H使得Θf=0时,有Sjf=0,∀j∈. 而{Sj}j∈是完全的,故f=0,进而Θ是单射. 设则由(4)式的左不等式易知Θ*也是单射. 即Θ 是满射;类似地,Θ*也是满射. 由逆算子定理可得Θ 和 Θ*都具有有界逆. 结合(5)式有 (6) 即{Sj}j∈是算子值q-框架. ∀k∈,由于Tk≠0,故可取f(k)∈H使得Tkf(k)≠0. 于是由(4)式得 从而mk=0,∀k∈,所以m|→Mm,(Tj),(Sj)是单射. 定理10 设Tj,Sj∈B(H,Hj),{Tj}j∈是算子值p-Bessel序列,{Sj}j∈是算子值q-Bessel序列,界分别是B1,B2,m={mj}j∈∈l∞,则M=Mm,(Tj),(Sj)连续依赖于{Tj}j∈,{Sj}j∈和m,亦即 (ⅰ) 若m(k)∈l∞,k=1,2,…, 且 ‖m(k)-m‖∞→0,则‖Mm(k),(Tj),(Sj)-Mm,(Tj),(Sj)‖→0(k→∞). 证明(ⅰ) 由命题5(ⅱ)可得 (7) 从而结论成立. (ⅱ) ∀f,g∈H,利用Hölder不等式得 因此 (8) 由此即知结论成立. (ⅲ)与(ⅱ)的证明类似. (ⅳ)由(7)和(8)可得 因此结论成立.1 算子值(p,q)-Bessel乘子