管道漏磁内检测矩形缺陷解析方法的分析

宁营超，杨理践，耿 浩,，夏 浩，高松巍

(1．沈阳工业大学 信息科学与工程学院，沈阳 110870；2．大连理工大学 工业装备智能控制与优化教育部重点实验室，大连 116024)

石油以及天然气主要采用铁磁性管道进行运输。铁磁性管道经过长时间的使用后，会产生腐蚀、老化等问题，而可能引发管道运输事故，给国家带来巨大的经济损失和环境污染。因此对油气管道进行定期的检测可以确保管道的安全运行[1]。管道漏磁内检测技术是目前管道安全检测最有效的方式，被广泛应用于长输油气管道的安全检测中[2]。漏磁内检测技术利用管道漏磁内检测器对管道进行磁化，使其达到磁饱和或者近磁饱和状态，便于检测器上的磁敏元件采集信号。检测器在管道内部移动时，其上的磁敏元件会采集到管道管壁的漏磁信号，并将采集到的信号进行存储转换。检测人员可通过采集到的漏磁信号特征来分析管道缺陷的大小、形状、位置等信息，为管道的后期维修提供有力的保障[3]。

管道漏磁内检测技术的关键是管道缺陷的尺寸、形状等特征与其漏磁场分布对应数学关系模型的建立，目前常采用的模型是磁偶极子模型和有限元分析模型。ZHANG等[4]基于线性磁荷理论建立了数值分析模型，采用三维微磁传感器检测腐蚀缺陷的泄漏场，为钢铁漏磁检测技术提供了数学理论。吴德会等[5]通过对缺陷不同磁化方向的磁化研究，建立了任意方向内表面缺陷漏磁场分布三维模型，对不同方向缺陷的漏磁场进行了描述。杜志叶等[6]采用有限元方法建立仿真模型，采用静磁场模型对缺陷的漏磁场进行了分析。时朋朋[7]以磁偶极子模型为理论基础，分析得到了梯形缺陷的二维磁偶极子模型，并拓展到矩形和V形缺陷的磁偶极子模型。LI等[8]采用磁偶极子方法，建立了地漏磁场梯度模量空间分布模型，分析了缺陷与梯度模量模型的定量关系。李忠吉等[9]基于现有的漏磁检测方法，建立了缺陷磁荷均匀分布的模型，并得到了磁荷实际分布下的缺陷漏磁场。仲维畅等[10-11]指出了矩形缺陷和圆柱形缺陷的磁荷分布规律，证明了磁偶极子理论对研究缺陷漏磁场分布的重要性。李红梅等[12]研究了三维磁化数值计算模型，推导出双层平面磁荷分布重构的有效算法。

文章在磁化方向与缺陷方向相垂直的条件下，研究了矩形缺陷磁荷在棱线上和侧壁上的分布情况，并对棱线上的磁荷密度和侧壁磁荷密度进行了求解，建立了缺陷漏磁场磁偶极子模型，对棱线磁荷和侧壁磁荷产生的漏磁场进行解算，完善了管道缺陷的磁偶极子模型理论，对管道缺陷识别具有一定的意义。

1 方法论述

1.1 管道漏磁内检测技术的基本原理

漏磁检测技术原理建立在铁磁性材料的高磁导率特性基础之上，通过励磁源对管壁进行充分磁化，使其达到磁饱和或近磁饱和状态，当管道中不存在缺陷时，磁力线平行于管道内部；当管道中存在缺陷时，部分磁力线被其表面或近表面的缺陷阻隔而泄漏到空气中，产生漏磁通。利用磁敏元件检测该漏磁信号，进而判断缺陷的存在性和特征，管道漏磁内检测原理如图1所示。

图1 管道漏磁内检测原理示意

1.2 缺陷磁荷分布

管道缺陷漏磁场解析计算主要以磁荷为纽带，分析缺陷处漏磁场的分布特征。磁荷模型把磁介质中的等量异号分子看作磁偶极子，磁化使磁偶极子之间产生力矩并转向磁场方向。漏磁场源于分布在缺陷两端的正负磁荷。磁介质未被磁化时，磁偶极子的分布是随机的，各个磁偶极子之间的作用力相互抵消，对外不显示磁性。当加入外加磁场H0对磁介质进行磁化时，外加磁场H0会对介质内的每个磁偶极子产生作用力，使磁偶极子向着外加磁场的方向移动。磁介质内部磁偶极子排列的方向与外加磁场的方向相同，内部磁偶极子有序排列。因此，磁介质宏观上对外显示磁性，磁介质被磁化。

由于同种磁荷之间存在相互作用力，随着磁化的进行，端面处的磁偶极子在相互作用力下向着侧面棱线处靠拢，最终聚集在缺陷的侧面棱线上。因此对有缺陷钢板进行磁化时，磁化除瞬间会在与磁化场相垂直的缺陷侧壁上激励出均匀分布的正负磁荷外，还会在缺陷附近的端面上激励出非均匀分布的净磁荷。由于磁荷间库仑力的存在，同种磁荷相互排斥，磁化完全后这些净磁荷会均匀分布在缺陷的棱线上。

磁介质中的磁化状态采用磁极化强度矢量J来表示，用公式表示为

(1)

式中：ΣPm为ΔV(体积)内所有磁偶极分子的磁偶极矩矢量和。

J还可表示为

J=χmμ0H0

(2)

式中：χm为磁介质的磁化率；μ0为真空磁导率。

将式(1)和式(2)联立可得

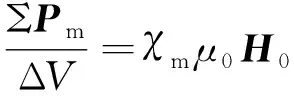
(3)

建立如图2所示的钢板矩形缺陷磁荷分布模型，缺陷的长度为2w，宽度为2b，深度为h，外加磁化场强的方向沿x轴正向。

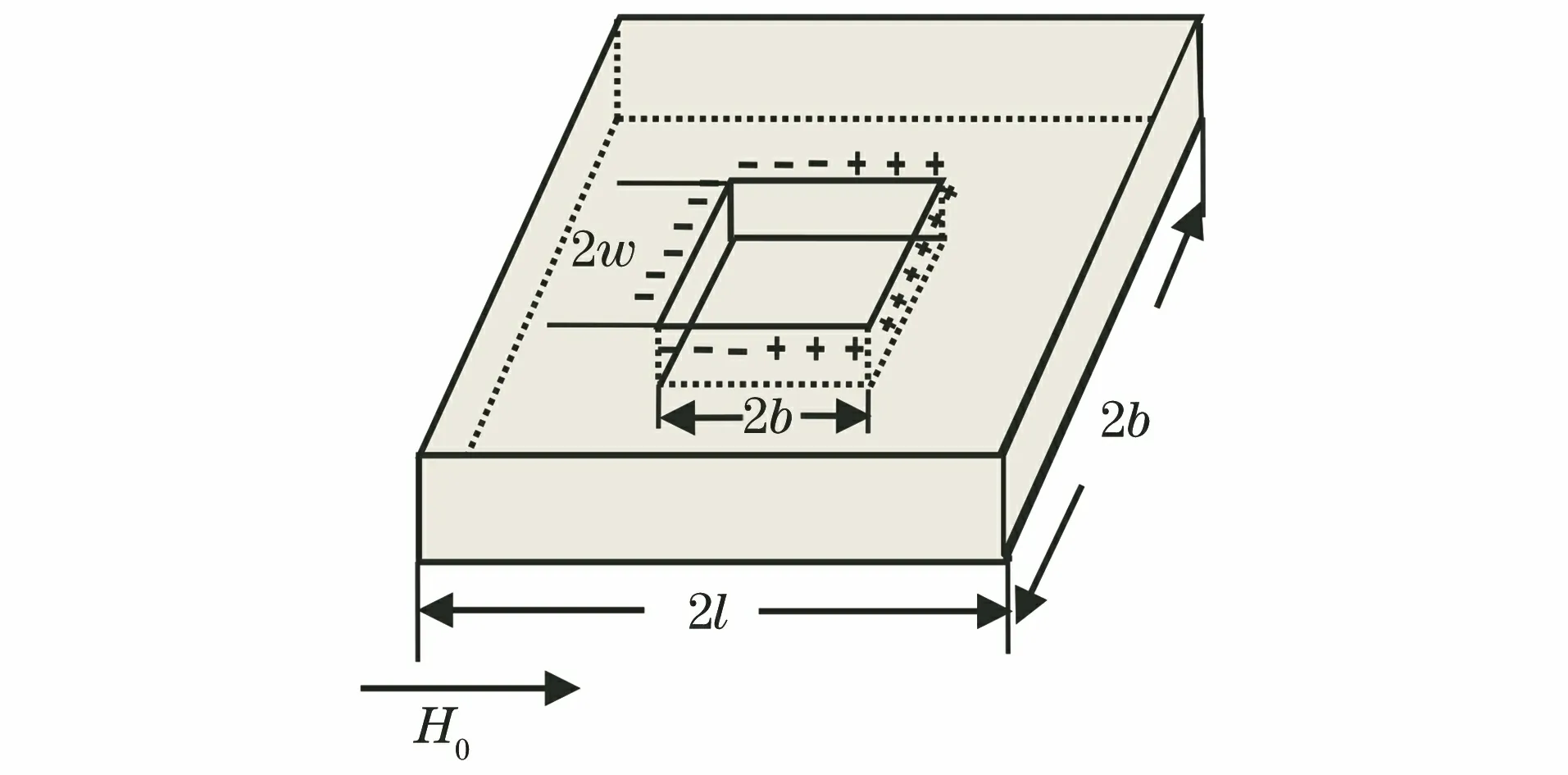
图2 钢板矩形缺陷磁荷分布模型

求得总的磁偶极矩为

P=4σ1(l2+2dl+h1l+b2+wl-wb)

(4)

式中：σ1为棱线磁荷密度，l为钢板宽度的一半，d为钢板长度的一半，h1为钢板厚度，b为缺陷宽度的一半，w为缺陷长度的一半。

联立式(3)和式(4)可得

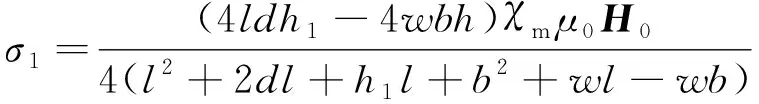
(5)

根据式(5)可知矩形缺陷的棱线处磁荷密度与缺陷的深度呈正比。研究发现，矩形缺陷两侧面的磁偶极子并非是均匀分布的，而是随着缺陷深度的变化而变化[13]。设磁荷在缺陷深度方向的变化率为u，则在每一个单位元dε上的磁荷密度为

dσs=udε

(6)

进一步得到面磁荷密度的表达式为

(7)

式中：μr为缺陷内物质的相对磁导率；σs的大小主要取决于其形状参数；z的取值为0～h。

通过研究磁偶极矩和磁极化矢量，得到矩形缺陷棱线处的磁荷密度以及缺陷侧面磁荷密度的大小，且发现棱线处的磁荷密度与缺陷的深度呈正比，缺陷侧面的磁荷密度随着缺陷深度的增加而减小。这为后文计算矩形缺陷漏磁场提供了依据，完善了缺陷漏磁场的解算模型，丰富了三维磁偶极子模型对矩形缺陷的数学描述。

2 矩形缺陷漏磁场求解

根据推导出来的矩形缺陷处的磁荷分布情况以及磁荷密度的大小，采用磁偶极子模型对矩形缺陷在空间中任意一点产生的磁场强度进行求解。建立三维磁偶极子模型，对矩形缺陷棱线处和缺陷侧壁产生的磁场强度进行计算，分别得到两者产生的漏磁场，并叠加在一起，即为钢板上矩形缺陷产生的总漏磁场的大小。

2.1 棱线漏磁场求解

棱线处的漏磁场采用线磁偶极子模型进行计算，设矩形缺陷的棱线长为2w，对称分布在矩形缺陷的两侧。矩形缺陷棱线磁偶极子模型如图3所示。

图3 矩形缺陷棱线磁偶极子模型

矩形缺陷两侧的棱线分布着正负两种磁荷，假设左侧棱线分布着正磁荷，右侧棱线分布的是负磁荷，左、右两侧的棱线上微元(xm，ym，zm)在p(x，y，z)点产生的磁场强度H1，H2为

(8)

(9)

式中：r1和r2为棱线上对应点到p点的距离，r1和r2为微元到p点的单位向量。

缺陷的棱线长为2w，因此对棱线上每一个小微元求积分，左侧棱线在各方向上产生的磁场强度为

Hx1=

(10)

Hy1=

(11)

Hz1=

(12)

右侧棱线在各方向上产生的磁场强度为

Hx2=

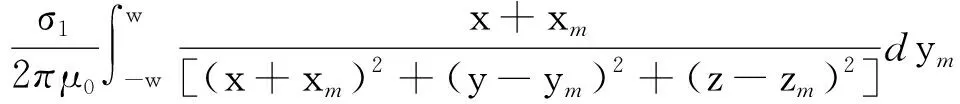
(13)

Hy2=

(14)

Hz2=

(15)

由于矩形缺陷两侧棱线分布着不同极性的磁荷，因此将左棱线和右棱线得到的磁场强度的表达式叠加可得

HX1=Hx2-Hx1

(16)

HY1=Hy2-Hy1

(17)

HZ1=Hz2-Hz1

(18)

由式(16)～(18)可知，在外加磁场H0的作用下，矩形缺陷棱线处建立的磁偶极子模型可以实现对矩形缺陷棱线处产生漏磁场的解算。磁荷非均匀地分布在矩形缺陷侧壁上，为了更加准确地解算矩形缺陷所产生的漏磁场，对缺陷侧壁磁荷产生漏磁场的解算同样重要。

2.2 侧壁漏磁场求解

设钢板上矩形缺陷的两侧壁垂直于磁化场H0的方向，建立矩形缺陷的三维磁偶极子模型如图4所示。

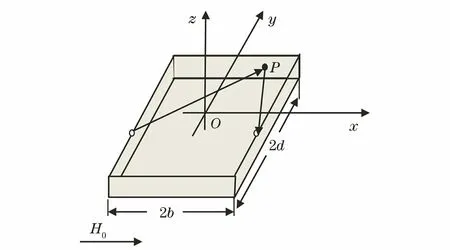
图4 矩形缺陷的三维磁偶极子模型

在缺陷侧壁上一个单位微元(xm，ym，zm)为dε。微元与P点的距离为r，根据点电荷的磁场分布，可以计算出缺陷侧壁单位磁荷在P点处产生的磁场强度dH为

(19)

式中：r3为微元到点P的距离;r3为微元到P点的单位向量;dp为单位面积内的磁荷总量。

dp=σs·dymdzm

(20)

式中：σs为曲线侧壁的表面磁荷密度；dymdzm为单位面积。

通过对单位面积磁荷产生的漏磁场进行积分，可以分别求解得到缺陷两个侧壁产生的漏磁场场强。通过矢量合成，可得到矩形缺陷产生的总漏磁场。缺陷左侧壁在各方向上产生的漏磁场为

(21)

(22)

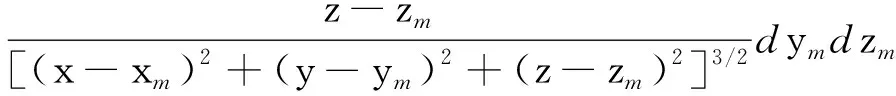
(23)

缺陷右侧壁在各方向上产生的漏磁场为

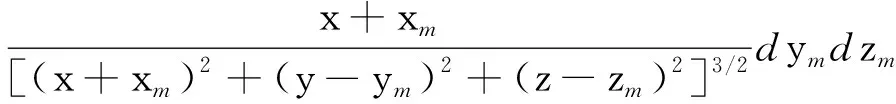
(24)

(25)

(26)

将x，y，z轴方向上的磁场强度进行矢量合成，即得到矩形缺陷两侧面产生的总场强为

HX2=Hx4-Hx3

(27)

HY2=Hy4-Hy3

(28)

HZ2=Hz4-Hz3

(29)

将棱线处产生的漏磁场与两侧壁产生的漏磁场进行矢量相加，即可得到矩形缺陷产生的漏磁场为

Hx=HX2+HX1

(30)

Hy=HY2+HY1

(31)

Hz=HZ2+HZ1

(32)

矩形缺陷的磁荷分布在棱线上和侧壁上，棱线上磁荷的分布是均匀的，侧壁上磁荷的分布是不均匀的。因此采用棱线上产生的漏磁场和侧壁上产生的漏磁场进行叠加，可以得到更加准确的缺陷漏磁场数据。

2.3 缺陷漏磁场模型仿真

缺陷的尺寸对其所产生的漏磁场大小具有直接影响。通过建立的三维磁偶极子数学模型，采用MATLAB数学建模软件对建立的数学模型进行仿真分析。

以所建立的模型为基础，分析矩形缺陷不同深度和宽度的漏磁场分布。设置缺陷长为20 mm，宽为8，10，12，14 mm，深度为1.7 mm。磁化场强度为120 A/m，钢板的相对磁导率为2 000,提离值设置为1 mm，将得到的数学模型用MATLAB软件进行仿真分析，设置x轴扫查位移为-20～20 mm，y轴扫查位移为-20～20 mm。得到不同宽度缺陷的漏磁场分布如图5所示。

图5 不同宽度缺陷的漏磁场分布

由图5可以看出不同宽度的矩形缺陷产生的漏磁场信号基本形态未发生改变，径向分量分布图位于原点两侧的波峰对应的x轴数值与矩形缺陷的宽度大小一致，轴向分量分布图中的波峰对应x轴的数值与矩形缺陷的宽度一致。径向分量漏磁场两峰之间的距离随着矩形缺陷宽度的增加而增加，轴向分量峰值两侧极值之间的距离随着缺陷宽度的增加而增加，轴向分量的幅值略微减小。由此可以看出，缺陷漏磁场的径向分量可以很好地反映出缺陷宽度的大小。

设置矩形缺陷宽度为10 mm，长度为20 mm，深度为1.6，1.8，2.0，2.2 mm，其他保持不变，得到不同深度缺陷的漏磁场分布如图6所示。

图6 不同深度缺陷的漏磁场分布

由图6可知，随着矩形缺陷深度的增加，缺陷漏磁场的径向分量和轴向分量基本形态不发生改变，二者峰值都随着缺陷深度的增大而增大，说明了缺陷深度的增加导致了磁通量泄漏增多。轴向分量两侧峰值的位置没有变化，说明缺陷的宽度没有变化。由此可知，缺陷漏磁场的径向分量和轴向分量可以很好地描述矩形缺陷的深度特征。

3 试验分析

为了验证所建立的缺陷漏磁场数学模型得到的漏磁场特征与工程实践中管道漏磁检测器获得结果的一致性，搭建了漏磁检测试验平台。通过使用外加励磁场对钢板进行磁化，将220 V交流电信号转换为直流电给线圈通电，模拟工程环境对钢板进行磁化。试验所用钢板上缺陷长为20 mm，宽为8，10，12，14 mm，深为1.6，1.8，2.0，2.2 mm。采用频率为2 000 Hz的漏磁检测探头进行缺陷漏磁检测，励磁线圈匝数为1800匝，探头距离缺陷1 mm。将试件匀速通过检测器，采集到的数据经过处理后如图7所示。

图7 试验得到的不同深度和宽度缺陷的漏磁场分布

如图7所示，随着缺陷宽度的增加，其漏磁场信号的峰值也增加。随着缺陷深度的增加，其漏磁场的峰值也随之增加。试验所得缺陷漏磁场的分布曲线与所建立的三维缺陷漏磁场模型所得的结果相符，验证了所建立模型的正确性。由此可以说明文章所提的解析模型(叠加棱线上磁荷与侧壁上磁荷产生的漏磁场)的有效性。

对比管道矩形缺陷棱线磁荷与侧壁磁荷叠加得到的缺陷漏磁场和假设磁荷均匀分布在侧壁得到的缺陷漏磁场，并计算误差，得到表1,2所示的磁荷非均匀分布和均匀分布下的缺陷漏磁场。

由表1，2可知，管道矩形缺陷采用棱线磁荷和侧壁磁荷叠加得到的缺陷漏磁场与工程实际得到的缺陷漏磁场的误差较小，采用磁荷均匀分布在侧壁上得到的缺陷漏磁场与工程实际得到的缺陷漏磁场误差较大。因此采用矩形缺陷棱线磁荷和侧壁磁荷叠加产生的缺陷漏磁场的结果优于假设磁荷均匀分布在侧壁上得到的漏磁场结果。

表1 缺陷磁荷均匀分布和非均匀分布下漏磁场轴向分量对比

表2 缺陷磁荷均匀分布和非均匀分布下漏磁场径向分量对比

4 结语

(1) 采用棱线磁荷与侧壁磁荷叠加得到的漏磁场的空间分布与试验所得数据具有相同形态和趋势。

(2) 管道缺陷漏磁信号与缺陷的深度具有线性关系，漏磁信号的峰值随缺陷深度的增加成比例增加，可根据漏磁信号峰值与峰峰间距确定缺陷的宽度。

(3) 文章所提的解析模型为管道漏磁内检测技术的解析方法研究提供了一种新的思路。