相控阵超声检测用喷水耦合喷嘴的优化设计

郭 猛，班 伟，刘露露，袁豪杨，陈嘉琪，姚 东

(1.宁夏大学 机械工程学院，银川 750021；2.国家管网集团西气东输公司银川输气分公司，银川 750021)

在我国提出“碳中和、碳达峰”的目标下，新能源需求不断增加，风力发电作为一种重要的清洁能源转换方法得到了迅速发展[1]。风机装机容量的提高对风机的寿命、可靠性等服役性能要求更为严苛，叶片作为风机中承受强风载荷的主要部件，其制造过程中的检测要求也不断提高。传统的检测方法如光照观察法、敲击法等，检测精度低，不易检测出叶片玻璃纤维外壳内部的缺陷，如孔洞、夹渣、分层、树脂纤维体积比不当等[2]。相控阵超声检测能灵活地控制声束扫描、偏转和聚焦等特性，在构件形状的适应性、检测参数的调整方面具有更多的自由度，已成为风机叶片等大型构件检测的重要方法。石一飞[3]分析了风电叶片褶皱、脱胶、干丝等多种缺陷的相控阵超声图像,证明了相控阵超声能够有效实现风电叶片的无损检测。ZHANG等[4]利用相控阵超声技术对多种叶片试样进行了缺陷检测，验证了该技术在风电叶片缺陷检测领域的可行性和适用性。

相控阵超声检测方法通常使用水作为耦合剂，可分为水浸式和喷水耦合式两种形式。与水浸式相比，喷水耦合式具有方便、快捷、检测范围大、避免工件长时间浸泡等优点，得到国内外学者的广泛关注。王炳方等[5]对喷水速度、喷水距离和喷水角度等参数对超声检测的影响进行了研究，提出了合理的参数选择范围；DEUTSCH等采用喷水耦合的方法对焊缝进行超声检测，证明了喷水耦合对复杂构件的适用性。目前喷水耦合存在的缺点主要是由射流不稳定而引起的声耦合稳定性较差，因此提高耦合水柱的射流稳定性是该技术得以进一步推广的关键。由于喷嘴内流道能够直接影响到水柱的射流状态[6]，需要对耦合喷嘴的内流道进行设计优化，以提高耦合水柱的射流质量。

为满足超声检测喷水耦合的需求，文章对4种不同结构的喷嘴进行了射流模拟仿真，选择了一种射流最为稳定的喷嘴，并从降低加工成本的角度进行考虑，对喷嘴进行了优化设计。

1 喷水耦合式相控阵超声检测系统

1.1 喷水耦合式相控阵超声检测系统组成

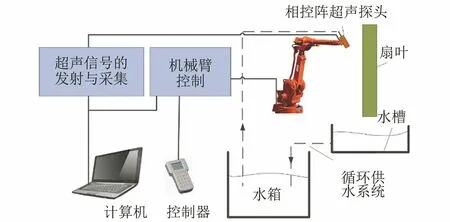
图1 喷水耦合式超声检测系统构成示意

1.2 喷水耦合原理

喷水耦合式相控阵超声检测系统通过超声信号的反馈对工件进行检测，超声信号从探头发出后沿耦合水柱进行传递。为防止水柱射流到工件表面产生剧烈飞溅，射流的速度不宜过大；为保证超声信号能够沿耦合水柱到达探头前方对应的工件检测区域，要求水柱在距工件30 mm的射流距离a内，且偏移量b应小于1 mm(见图2)；为减少超声信号在传递过程中的衰减，保持信号的声耦稳定性，要求耦合水柱状态稳定、集束性好。

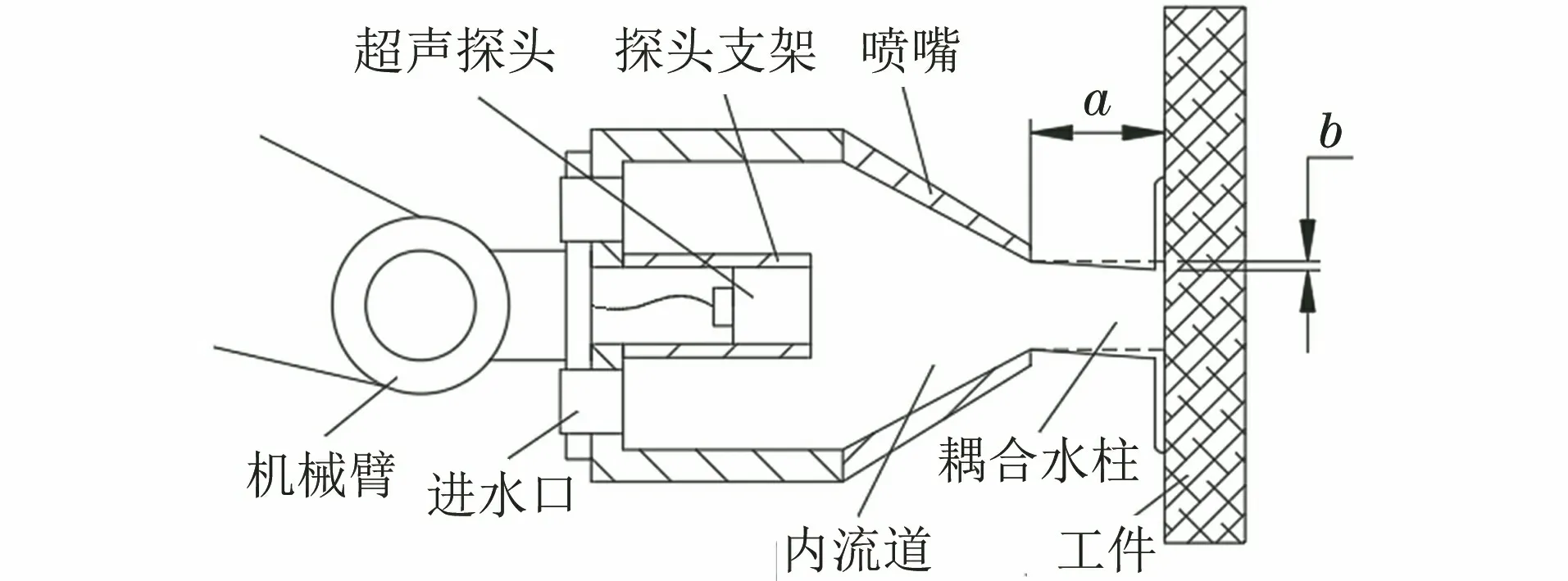
图2 超声喷水耦合原理示意

1.3 相控阵超声探头工作原理

常见的超声阵列有线性、二维阵、环形阵等多种形式，不同的超声阵列适用于不同的检测情况[7]。文章设计从降低成本和适用于大型复杂构件的检测方面来考虑，选用线性相控阵，该类型超声探头内的条形压电晶片呈线性排布，探头的形状为矩形。因为喷水耦合式相控阵超声信号的传播是沿着耦合水柱传播的，所以需要设计合适的矩形出水口喷嘴便于超声探头的喷水耦合。

2 喷嘴的参数及结构设计

2.1 喷嘴的参数设计

相控阵超声探头发出的超声声场理论上覆盖探头的整个前方，但声场边角的检测效果较差，所以将发射范围定义为一个由检测精度确定的有效范围[8]，喷嘴出口的大小应根据此范围进行确定。文章所选用的相控阵超声探头信号发射面的长为66 mm，宽为20 mm，发射超声波有效范围的角度约为100°。从降低喷水耦合过程中超声信号的衰减和降低喷嘴的整体质量方面考虑，应尽量减少超声探头与喷嘴出口截面的距离。为了减少超声探头对喷嘴射流的影响，探头距喷嘴出口截面的距离应略大于喷嘴过渡段的长度。所设计的喷嘴过渡段的长度为90 mm，超声探头距喷嘴出口的距离为95 mm。喷嘴出口处超声检测有效范围的长度为

L=2h·tan(a-90°)+l

(1)

式中：L为喷嘴出口处超声检测有效范围的长度；h为探头距喷嘴出口的距离；a探头发射超声波有效范围的角度；l为探头的长度。

计算可得在距探头信号发射面95 mm的喷嘴出口处，超声检测有效范围的长度约为100 mm，因此所设计喷嘴出口长度为100 mm。

由于探头阵元沿长度方向排列，所以喷嘴出口的宽度在理论上只需要与超声探头的宽度相同即可。考虑到探头安装过程中可能存在一定的角度偏差，在设计中应保有一定的余量。文章设计喷嘴出口的宽度为30 mm。

2.2 喷嘴结构设计

单一进水管道所产生的弯折应力较大，机械臂运动时易产生抖动。为降低机械臂抖动对检测精度的影响，进水端设计为3个均匀布置的进水口，与3条DN 40的管道连接。为减少水流进入喷嘴内腔而产生旋流，喷嘴进水口与出水口采用平行式水路设计。

智慧科研是将信息化理念深入到科学研究、科学应用以及科研项目管理中。通过统一的数据模型，提供与项目相关活动的准确的各角度视图，使科研主管部门能够为项目分配合适的资源，确保项目执行并跟踪项目的成果，从而提升科研院所的科研能力及效率；将科研成果、获奖情况以及日常的科研活动及时记录下来，便于查询统计，并促进专家资源库、专利资源库、学术资源库的建立和完善；对科研活动科研人员进行自动绩效考核，免去人工统计的烦恼，使得工作更加高效、协同。

喷嘴通常设计成锥形收缩结构，其边壁收缩处为转折突变，易产生紊流旋涡区，而使用维多辛斯基曲线设计的喷嘴内腔壁面平滑，能使进入喷嘴收缩处的水流横向压力梯度和径向分速度逐渐减小，得到较为稳定的射流流束。为研究适用于相控阵超声检测的耦合喷嘴内流道结构，设计了3种常见的喷嘴和一种维多辛斯基曲线喷嘴。维多辛斯基曲线如图3所示，曲线计算公式如式(2)所示。不同喷嘴的内腔结构如图4所示。

图3 维多辛斯基曲线

(2)

图4 不同喷嘴的内腔结构示意

式中：h1，h2，y分别为过渡段进口、出口及任意x处截面对应高的一半；L为喷嘴过渡段的总长度。

3 喷嘴射流仿真分析

3.1 流场几何模型的建立

优化设计主要针对喷嘴内流道，在建立喷嘴射流流场模型时暂不考虑喷嘴内部构件。以锥形喷嘴为例，建立起的流场模型如图5所示。

图5 锥形喷嘴流体域模型(半剖图)

3.2 仿真边界条件的设定

喷嘴射流水柱主要受重力影响向下偏移，根据射流水柱在30 mm的射程内，偏差小于1 mm的要求，通过计算可知射流水柱的最低流速为2.1 m·s-1。又知射流速度过大易产生溅射，通常在进行超声检测时，耦合水柱流速为0.8～3 ·s-1，透射信号的波动小，检测效果好。在保有余量的前提下，设计喷嘴出口的流速为2.5 ·s-1，计算得喷嘴入口的流速约为2 ·s-1。对求解器进行设定时，以水流速度入口和速度出口为边界，并将计算所得的流速等系数代入求解器。

3.3 喷嘴射流仿真结果与分析

在进行相控阵超声检测系统射流仿真分析时，由于喷嘴的出口为方形，所以需要对同一喷嘴流体域的xy截面和xz截面的射流情况进行分析，又考虑到射流偏移量的要求，还需对距喷嘴出口30 mm处的yz截面进行速度分布分析。

相同条件下4种喷嘴xy截面和xz截面速度分布的仿真结果如图6所示。

图6 4种喷嘴xy截面和xz截面的速度分布

由图6的射流仿真可知，各喷嘴由于内流道结构不相同，速度分布也不相同，其中锥形喷嘴的速度分布不均匀，存在明显的速度差，易产生紊流，速度发散较快；直角形喷嘴速度衰减较大，水流从3个进水口进入后未能在喷嘴内部得到有效的整流，射流发散明显；锥直形喷嘴射流稳定，但因过渡段较短，仍存在明显的速度差，且整流效果较差，射流发散快；维多辛斯基曲线喷嘴中射流速度变化主要集中在过渡段，由于过渡段为曲线，所以速度变化为柔性变化，无明显速度差，射流较为稳定不易产生紊流，且射流集中，速度发散较为缓慢。

距喷嘴出口30 mm处4种喷嘴yz截面的速度分布如图7所示，图中黑色框线代表喷嘴出口在工件上的对应位置。

图7 距喷嘴出口30 mm处4种喷嘴yz截面的速度分布

由图7的仿真结果可知，锥形喷嘴和锥直型喷嘴的射流覆盖效果较差，均呈现出两边高中间低的情况。直角形喷嘴的射流水柱速度分布面积较广，但存在明显的速度分布差，射流水柱不够稳定。维多辛斯基曲线喷嘴射流水柱稳定，速度分布均匀，向下偏差较小。

通过对喷嘴射流的仿真分析可以发现，锥形、直角形以及锥直型喷嘴的射流均存在一定的缺陷，相比之下维多辛斯基曲线喷嘴过渡良好，射流稳定，射流水柱能较好地覆盖工件上对应的超声检测区域。

4 喷嘴的优化设计

4.1 道格拉斯-普克算法实现喷嘴的近似设计

文章设计的喷嘴存在一定的加工困难，特别是维多辛斯基曲线喷嘴在制造时，要以维多辛斯基曲线作为引导，加工精度难以保证。因此在进行喷嘴设计时，需要采用一种近似方法，对维多辛斯基曲线喷嘴进行近似设计，以达到在降低加工难度的同时，保持较优的射流效果。

道格拉斯-普克算法是线状要素抽稀的经典算法，采用该算法可以保留曲线较大弯曲形态上的特征点，删除较小弯曲上的特征点，有效地保持曲线的形态特征。通过维多辛斯基曲线喷嘴内部压力的分布(见图8)可知，喷嘴内部压力差变化较大的区域主要集中于水流刚进入过渡段处和水流刚进入平缓流道处，与曲线弯曲形态较大的部分相对应。因此可以采用道格拉斯-普克算法得到维多辛斯基曲线的近似折线，对维多辛斯基曲线喷嘴进行近似设计。

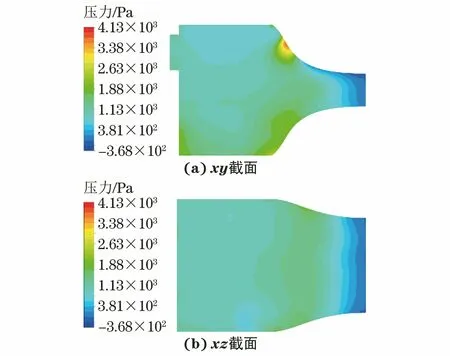
图8 维多辛斯基曲线喷嘴内部压力分布

道格拉斯-普克算法的步骤如下所述。

(1) 连接曲线的首末端点A、B，得到一条直线，找到曲线上所有点与该直线距离最大的点C，最大距离记为d。

(2) 比较该距离d与事先定义的阈值D的大小，若dD，则通过点C把曲线分成两段重复上述步骤。

(3) 当曲线处理完毕时依次连接各分割点形成的折线，即为该曲线的近似折线。

采用道格拉斯-普克算法来实现维多辛斯基曲线的近似时，通常设置的阈值越小、选取的点越多、划分的线段越多、近似效果越好，但较多的分段又会增加加工难度。在进行曲线近似线段划分时，要在消除掉曲线上较为明显的弯曲形态特征点的基础上尽量减少分段。综合考虑后设置曲线的近似折线线段为4段，绘制维多辛斯基曲线的近似折线结果如图9所示。

图9 维多辛斯基曲线的近似折线

文章根据道格拉斯-普克算法实现维多辛斯基曲线的近似分段，在维多辛斯基曲线喷嘴的基础上设计了一种四段式喷嘴。由于喷嘴的出口为长方形，在xy平面上的曲线与xz平面上的曲线并不相同，得出的近似线段的节点也并不相同，无法同时作为放样引导线。分析可知xz平面上维多辛斯基曲线坡度变化较小，对喷嘴射流的影响较小，在设计时可仅在坡度变化较大的xy平面上采用道格拉斯-普克近似线段进行引导。设计出的四段式喷嘴外形如图10所示。

图10 四段式喷嘴外形

4.2 四段式喷嘴的仿真验证

该四段式喷嘴除过渡段轮廓外，其他参数与上述4种喷嘴均相同。对该四段式喷嘴进行仿真分析，得到其流速场分布如图11所示。

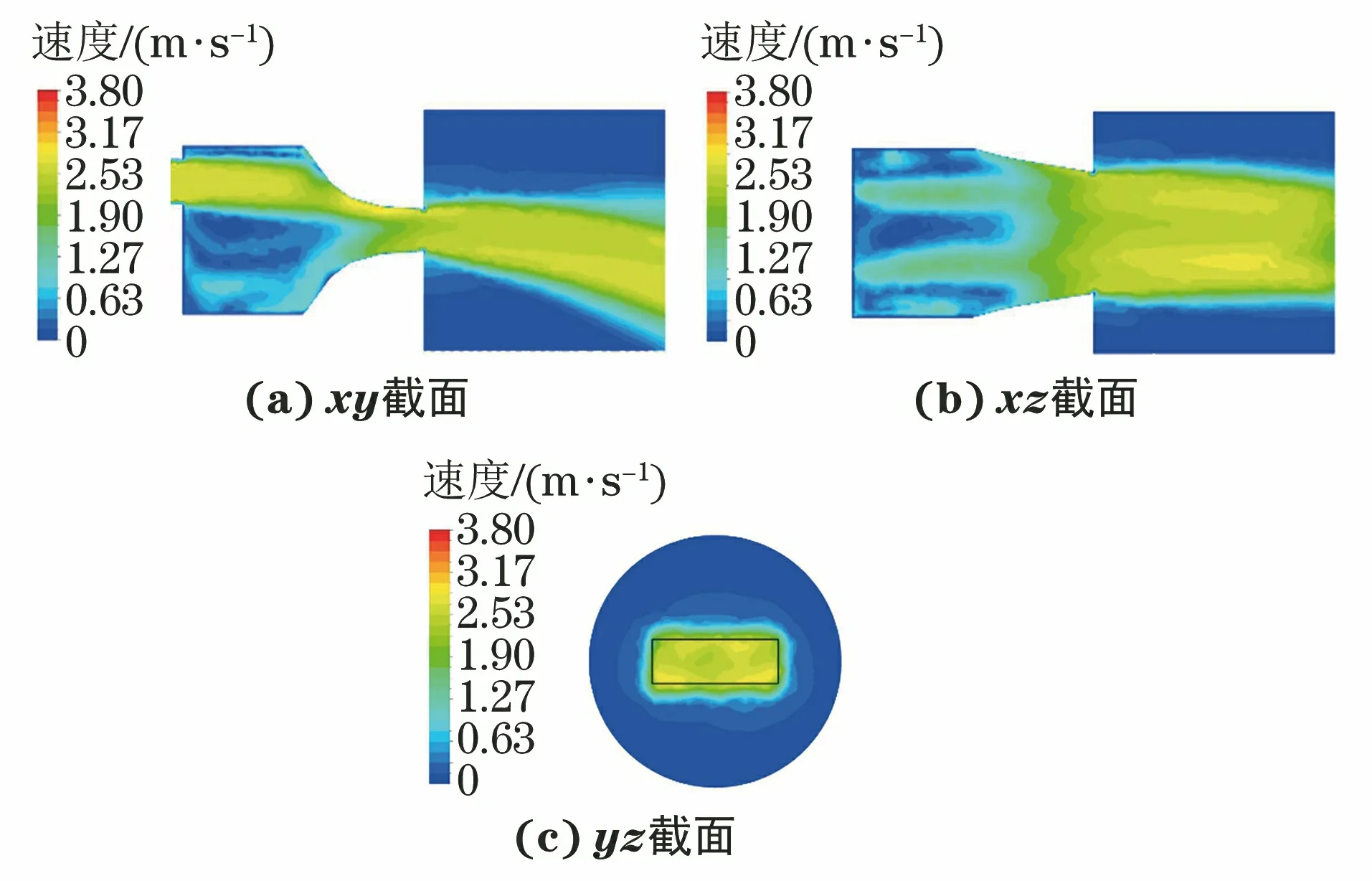
图11 四段式喷嘴速度流场分布

由图11中的仿真分析可知，依据道格拉斯-普克算法近似设计的四段式喷嘴射流速度分布均匀，流束集中，水流能够完全覆盖对应检测的工件区域，且与维多辛斯基曲线喷嘴的射流仿真分析对比，也未发现有明显的射流发散现象。

5 结语

(1) 喷水耦合式相控阵超声检测系统耦合水柱的状况能够直接影响到超声检测信号的传递，喷嘴内流道的轮廓曲线是影响射流的重要因素。

(2) 对比4种喷嘴射流的仿真结果可知，以维多辛斯基曲线作为引导线设计的喷嘴，其射流水柱质量较高，耗散率低。

(3) 维多辛斯基曲线喷嘴加工较为困难，在维多辛斯基曲线喷嘴的基础上，根据道格拉斯-普克算法设计了一种四段式喷嘴，使其在降低加工难度的同时还能保持较好的射流情况，该喷嘴适用于相控阵超声检测系统的喷水耦合。