基于粒子群算法优化的步进电机转速控制方法研究

贾蒙蒙,胡东芳,许启跃,叶树亮

(中国计量大学 计量测试工程学院 工业与商贸计量技术研究所,浙江 杭州 310018)

步进电机是一种将电脉冲信号转变为直线位移或角位移的控制元件,在工业生产、医疗器械、航空航天等方面具有广泛的应用。步进电机具有非线性、强耦合的特点,在开环位置控制下难以得到满意的控制结果。因此,选择一种合适的控制策略,可以有效提高步进电机的控制精度,实现电机的高效控制。林法正[1]介绍了基于数字信号处理器(digital signal processor, DSP)的永磁同步电机驱动系统,利用最小二乘法和实时比例积分位置控制器,实现了电机的基础控制。该方法不依赖于电机的参数模型,但由于电机控制中未使用微分项,控制效果不佳。Rubaai A等[2]提出了一个集成环境的快速原型的鲁棒模糊比例积分微分(proportional integral differential,PID)控制器,该模型在处理非线性和外部干扰方面具有更好的控制性能,缺点是该方法不具有普适性。兰建武等[3]将自适应模糊推理算法运用在电机的旋转控制中,优化其控制参数和性能,提高了电机运行的平稳性,但在使用过程中需要考虑并制定控制过程中的各参数模糊子集的隶属度赋值表和各参数的模糊调整规则模型,使模糊规则的制定更加困难。

本文引入了粒子群算法优化模糊PID(PSO-fuzzy PID)[4-5]控制算法对步进电机进行转速控制,PSO-fuzzy PID控制算法在机器控制、车辆控制、锅炉控制等方面具有突出应用。该控制算法不仅可以实现对步进电机的高效控制,通过粒子群算法还可以实现对模糊控制器的在线迭代寻优,从而弥补了模糊规则难以制定的缺点。通过对模拟与实验结果的分析研究表明,PSO-fuzzy PID的控制算法较之常规模糊PID和PID控制,解决了模糊规则难以制定的缺点并提高了系统控制的平稳性、快速性。

1 步进电机数学模型的建立

建立步进电机控制系统首先要对步进电机进行数学建模[6]。对于两相混合步进电机,以A相为代表,其单相绕组的等效电路图如图1[7]。其中,Ra表示A相绕组的电阻;La表示A相绕组的电感;ea(θ)表示该电机的反电动势;Ua表示A相绕组的电压。

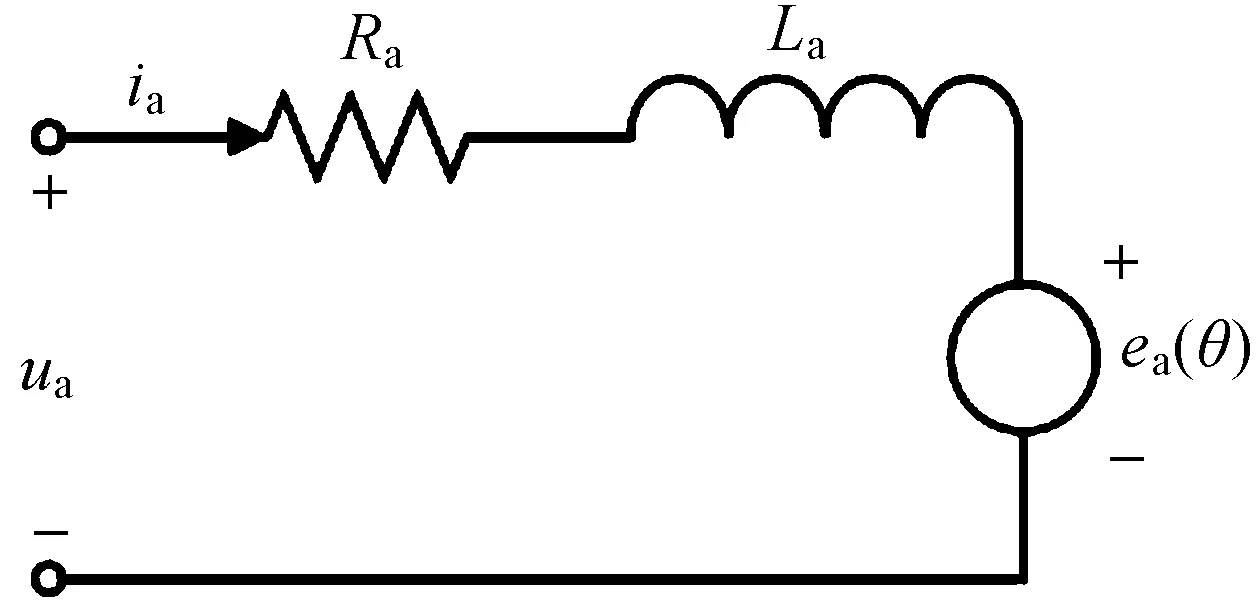
图1 两相混合步进电机单相等效电路

两相混合步进电机的电压平衡方程和电磁转矩分别为式(1)(2)[8]

(1)

(2)

其中,Ua、Ub、ia、ib分别为A、B两相的绕组电压与绕组电流,L0为两相间的互感,Zr为转子齿数,Te为电磁转矩,J为转动惯量,D为粘性系数,TL为负载转矩。当两相励磁处于平衡位置时,即转子稳定在β/2时,平衡位置步进电机通电相的电压方程式为:

(3)

其中,L为自感;M为互感;Kf为永磁体和相绕组的耦合系数。则步进电机的传递函数模型如下:

(4)

以单相励磁为例,假设负载转矩TL=0,可以得到步进电机的运动方程为

(5)

对式(5)作拉式变换处理,得到

(6)

式(6)中,θ0(s)为步进电机的理论转动角度,θi(s)为步进电机的偏差转动角度,Kp为步进电机阻尼系数,ωn为步进电机固有角频率。两相励磁时在平衡位置扰动微小,在s=0时,振荡值应恢复在平衡位置θi上,G(s)=1,两相励磁情况下的传递函数表示为

(7)

式(7)中,Lp=L-M,Kp为步进电机的阻尼系数,ωnp为步进电机固有角频率。本文研究的步进电机参数如表1。

表1 步进电机参数

由步进电机的参数计算得到步进电机两相励磁传递函数为

(8)

2 粒子群算法优化的模糊PID

2.1 粒子群算法

粒子群算法(particle swarm optimization,PSO)[9-10]是通过模拟生物捕食的迭代优化算法。当其初始化后,每个随机粒子为了得到最优目标解,会根据自身的历史最优情况和整个种群的历史最优情况来调整自己的行为模式,即速度更新策略。在经过多次迭代之后,寻找到目标函数的最优解。在每一次迭代[11]过程中,每个粒子的情况都会被评估,因此,速度更新策略[12]对粒子群算法的结果十分重要。粒子群算法的速度更新策略如图2。

图2 粒子速度更新示意图

2.2 适应度函数

PSO优化包括设计优化目标,即适应度函数,然后对要搜索的参数进行编码。PSO算法运行直到满足停止条件。最佳粒子位置给出了优化的参数。时间乘以误差绝对值积分(integrated time and absolute error,ITAE)[13-14]通常是一种评价工程实用性和选择性的指标,因其具有快速、平稳、超调量小等特点,因而被广泛应用于实际工程问题中,其表达式为[15]

(9)

式(9)中,tk是当前仿真的时间;e(t)为给定力矩与实际力矩之间的差值,k为加权系数,E(t)∈e(t),为e(t)中的任意值。

2.3 迭代寻优

粒子群算法最重要的步骤便是迭代寻优过程,在迭代寻优过程中,每个单独的粒子都具有以下特性[16]:n为初始粒子个数,xi为粒子当前位置;yi为当前搜索范围内的最佳位置;vi为粒子的速度;ybest为群体最优位置,通过不断迭代寻找目标的最优解。

式子(10)及(11)描述了粒子的当前最优值和群体最优值的选取,假设粒子群中粒子数为n,i∈n:

(10)

ybest(t)=min{f(y),f(ybest(t))},y∈{y0(t),y1(t),…,yn(t)}。

(11)

在粒子的迭代过程中,其速度和位置更新步骤为:

vi,j(t+1)=ωvi,j(t)+2r1(t)[yi,j(t)-xi,j(t)]+
2r2(t)[ybest(t)-xi,j(t)],

(12)

xi(t+1)=xi(t)+vi(t+1)。

(13)

其中,r1,r2为[0,1]之间的随机数,ω为惯性因子,惯性因子是根据以下方程决定的:

(14)

其中,λ为当前迭代次数,λmax为最大迭代次数。

2.4 粒子群算法优化的模糊PID

本文提出了一种基于粒子群算法优化的模糊PID控制器(PSO-fuzzy PID),结构框图如图3。

图3 PSO-fuzzy PID结构框图

由图3可得,输入步进电机目标转速后,PID控制器输出控制信号至步进电机,得到实际转速,计算得到转速误差e与误差变化率ec,改进的粒子群算法对模糊PID的隶属度和规则库进行优化,经由模糊PID控制器输出增益变化ΔKp、ΔKi、ΔKd,增益变化与PID控制器结合运算得到输出控制信号,完成对步进电机的转速控制。

其中,设置粒子个数30个,学习因子c1=c2=2,维度151,速度最大值为1完成对粒子群算法参数设计的初始化。

粒子群算法的优化分为两个部分:一是隶属度函数,二是模糊控制规则库。最优隶属度函数的迭代寻优,以单个粒子为例,设置隶属度函数的底宽为寻优目标,当初始化完成且粒子完成一次飞行后,更新粒子的速度与位置,将当前得到的隶属度函数用于模糊控制器中。经过不断的飞行迭代可以得到动态隶属度函数并对步进电机进行控制,获得该次迭代所得到的控制指标,例如超调量、转速误差、误差变化率、调节时间等,计算并返回适应值得到并更新局部最优值和全局最优值,完成一次迭代。循环以上步骤直到循环结束得到最优隶属度函数。

对于模糊控制的控制规则,将模糊控制规则表的成员函数{NB,NM,NS,Z,PS,PM,PB}对应十进制索引值数字{1,2,3,4,5,6,7}。反应过程中模糊PID的输出为增益变化ΔKp、ΔKi、ΔKd,其对应十进制的编码长度为3×7×7=147。反应开始的第一个粒子使用专家经验所列写的规则表进行初始化,降低寻优难度,初始化该粒子速度值,并随机生成其余粒子的速度与位置,沿用隶属度函数,将新生成的模糊控制规则与隶属度函数相结合生成模糊PID控制,输出增益变化ΔKp、ΔKi、ΔKd,计算PID参数并返回,输出转速完成转速控制。

根据上文建立的基于两相步进电机的传递函数作为被控对象,将式(7)作为被控对象,进行初步的仿真验证。基于粒子群算法优化的模糊PID控制器仿真模型如图4。

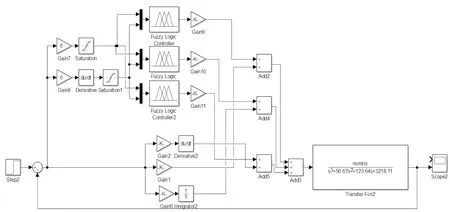
图4 基于粒子群优化模糊PID的两相步进电机控制器仿真模型

3 仿真结果

为测试粒子群算法优化的模糊PID算法的性能,使用MATLAB/Simulink对两相步进电机进行建模,其中,PSO-fuzzy PID的模糊控制器隶属度函数及规则库经过粒子群算法在线迭代优化后粒子群算法的适应值如图5。

图5 粒子群算法适应值Figure 5 Particle swarm optimization algorithm fitness

由图5可知,当迭代次数达到20次左右时,粒子群算法适应值趋于稳定,参数收敛,PSO算法的优化过程中经历了8次迭代最后得到最优解。此时最优个体为优化后得到的模糊控制规则如表2—表4,隶属度函数如图6。

表2 粒子群算法优化后ΔKp规则库

表3 粒子群算法优化后ΔKi规则库

续表3

表4 粒子群算法优化后ΔKd规则库

图6 粒子群算法优化后的隶属度函数

利用Simulink模块进行仿真,以单位阶跃信号作为输入信号,分别在三种控制方法下进行系统仿真,输入PID参数P=0.072 4;I=0.688;D=3.454,三种控制方法均使用此PID参数,仿真结果如图7。分析图7中的仿真曲线可得,PSO-fuzzy PID在三种控制方法的比较下,控制效果最为理想,满足系统的稳态特性。

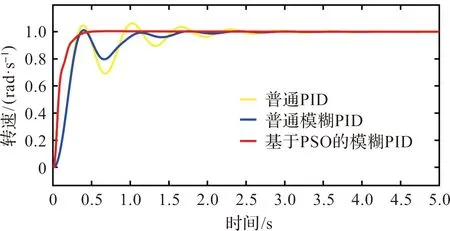
图7 基于PID、模糊PID、粒子群算法优化模糊PID仿真曲线图

4 步进电机转速控制实验

针对两相步进的转速控制要求,选用STM32作为主控芯片,建立一种基于STM32的粒子群算法优化模糊PID的步进电机转速控制系统。系统包括主控模块、驱动模块、启动模块、电源模块、光耦隔离、通讯模块及上位机监控模块,系统框图如图8。

图8 步进电机转速控制系统框图

该控制系统以STM32作为主控芯片,启动模块完成对步进电机的启动,电源模块为步进电机与主控板其余模块提供电压,光耦隔离模块可以防止外部电流倒灌,增强驱动能力,驱动模块连接步进电机驱动器,实现对步进电机的细分控制。编码器为转速反馈元件,将检测到的实际脉冲个数反馈给主控模块,主控模块根据检测到的脉冲个数与目标脉冲个数的数量相比,计算e与ec,将模拟所得控制表存放在软件内,软件根据e与ec的实时更新,进行查表后可以得到实时输出控制信号。STM32根据算法产生的控制信号输出脉冲个数,完成对转速的控制,具体的软件流程如图9。

图9 粒子群优化模糊PID软件控制流程图Figure 9 Flow chart of PSO-fuzzy PID software control

通过硬软件设计以及上位机监控模块,可以对步进电机的转速数据进行实时的读取与保存。输入目标转速为10 rad/s,得到在PID算法、模糊PID算法和PSO-fuzzy PID控制下的步进电机转速控制效果如图10。

图10 电机转速实验图Figure 10 Motor speed experiment diagram

由图10可以看出,在控制目标为10 rad/s的情况下,步进电机在粒子群优化的模糊PID算法的控制下,达到稳定速度的响应时间最短,超调量最小,在速度达到稳定状态后不产生振荡现象。可以证明PSO-fuzzy PID可以实现对两相步进电机速度的高效控制,是一种优异的控制算法。

5 结 语

本文针对两相步进电机的非线性控制,提出了一种基于粒子群算法优化的模糊PID控制器(PSO-fuzzy PID)。采用改进的粒子群算法在线迭代计算模糊PID控制器的隶属度函数和控制规则,直到得到最优解。利用两相步进电机的数学模型在Simulink仿真环境下,建立了电机的转速控制系统,同时设计并搭建了基于STM32的两相步进电机软硬件控制平台,测试了PSO-fuzzy PID的超调量、稳定时间、适应度函数等性能,结果表明,PSO-fuzzy PID的控制性能明显优于其他控制器,该算法有望应用于对步进电机的转速控制精度要求高的场合。