Self-adaptive Bat Algorithm With Genetic Operations
Jing Bi,,, Haitao Yuan,,, Jiahui Zhai,,,MengChu Zhou,,, and H. Vincent Poor,,
Abstract—Swarm intelligence in a bat algorithm (BA) provides social learning. Genetic operations for reproducing individuals in a genetic algorithm (GA) offer global search ability in solving complex optimization problems. Their integration provides an opportunity for improved search performance. However, existing studies adopt only one genetic operation of GA, or design hybrid algorithms that divide the overall population into multiple subpopulations that evolve in parallel with limited interactions only. Differing from them, this work proposes an improved selfadaptive bat algorithm with genetic operations (SBAGO) where GA and BA are combined in a highly integrated way. Specifically,SBAGO performs their genetic operations of GA on previous search information of BA solutions to produce new exemplars that are of high-diversity and high-quality. Guided by these exemplars, SBAGO improves both BA’s efficiency and global search capability. We evaluate this approach by using 29 widelyadopted problems from four test suites. SBAGO is also evaluated by a real-life optimization problem in mobile edge computing systems. Experimental results show that SBAGO outperforms its widely-used and recently proposed peers in terms of effectiveness,search accuracy, local optima avoidance, and robustness.
I. INTRODUCTION
AS a nature-inspired algorithm of meta-heuristic optimization, a bat algorithm (BA) has been adopted to tackle various types of complicated benchmark and engineering optimization problems since its inception [1] in 2010.Simulating their echolocation behaviors of bats, a group of bats interact and cooperate to locate and find their prey/solutions. They also identify distinct types of insects even if they are in complete darkness. BA is easy to implement and exibits high search efficiency. It has been chosen to solve different real-life engineering optimization problems in various areas,e.g., image classification [2], wireless sensor networks [3],autonomous mobile robots [4], economic dispatch [5], and power flow optimization [6].
However, bats in the standard BA maintain learning from the globally best solution obtained so far. Therefore, its finally obtained solutions to many industrial engineering problems may be unsatisfying. To tackle this drawback, many BA variants that use various methods and strategies are proposed.They can be separated into six types: 1) mutation methods [7];2) improved velocity updating methods [8], [9]; 3) hybrid methods [10], [11]; 4) neighborhood search schemes [9], [12];5) parameter adjustment [13], [14]; and 6) multi-objective BAs [15], [16]. Although they can improve the performance of BA, most of them fail to maintain all desired advantages or features like high population diversity, avoidance of premature convergence, fast convergence, and high accuracy over different types of problems. For example, some variants[10] can improve the diversity of population and tackle a premature convergence issue, but their convergence speeds are unsatisfactory. Some variants, e.g., [17], fail to find global optima for some complicated optimization problems with multiple local optima. Thus, it is challenging to universally improve the overall performance of BAs for their various applications.
It has been shown that behaviors of individuals, e.g., bird foraging and migration [18], and bee scouting [19], are significantly affected by their corresponding genotype information. For example, according to [20], foraging behaviors of individuals are primarily determined by their evolutionary processes rather than their foraging environments. On the other hand, skills of individuals obtained from their social activities can influence their selections, and thus, change the genotype information in the current population [21]. Biological experiments have concluded that the genotype information and behavior of individuals affect each other.This provides an opportunity to adopt such relations between them to improve the performance of BA as inspired by the biological models [22].
BAs’ performance can be limited for some real-life problems due to their limited learning ability. The genetic operations of the genetic algorithm (GA) provide a promising way to tackle BA’s drawback. Thus, many techniques have been proposed for increasing BA’s performance by incorporating genetic operations of GAs into BA. They fall into two types. The first type of techniques [23], [24] aim to improve one single genetic operation of BA, e.g., selection, mutation or crossover of GAs. The second type of studies propose hybrid algorithms by integrating BAs and GAs. For example, Xu and Cheng [25] propose a hybrid genetic bat algorithm for minimizing the makespan of scheduling problems by adopting a neighborhood search of a GA’s mutation and hybrid crossover operation. We consider that GAs and BAs can be combined in more cohesive ways. For example, our genetic operation of a GA can yield exemplars from which bats learn,and in turn, pass their results back to GA to guide the evolution of GA’s exemplars. Latifet al. [26 ] propose a hybrid algorithm for overcoming the tendency of BAs toward early trapping into local minima. They apply a GA’s mutation after the construction of updated solutions produced by a BA to improve solution diversity. We can well avoid the premature convergence problem associated with BAs by using highdiversity exemplars produced by GA’s genetic operations.Yue and Zhang [17] present a hybrid BA with a GA’s crossover operation to strengthen local search capability. They apply an adaptive updating method of inertia weight for good balance between exploration and exploitation. We combine GA and BA in a cascade hybrid manner, and jointly adopt selection, crossover and mutation operations of GA to guide a search process of BA. Dizaj and Gharehchopogh [27]combine GA and BA in a sequential manner. Specifically,they first adopt BA to yield the best solution, which is further transferred to GA. Then, they conduct the selection, crossover,and mutation of GA on it to further produce the final best solution. We combine GA and BA with an alternative feedback loop to help bats find the optimum. Hybrid algorithms based on combing GAs with BAs have been adopted to solve such practical problems as image segmentation [17], application placement in clouds [23], knapsack problems [24], job shop scheduling [25], and energy management [26].
A majority of the above-mentioned hybrid algorithms divide the entire population into two subpopulations that evolve in parallel. GA and BA control each subpopulation, and recombine their produced subpopulations. Their relations and interactions are relatively weak and loose. It is difficult to distinguish how individuals in a subpopulation produced by GA affect that by BA. It is challenging to investigate how individuals in a subpopulation produced by BA affect that by GA. In addition, most hybrid algorithms are tested and evaluated with single-type or low-dimensional benchmark optimization problems only. It remains an open problem of how to efficiently combine BA and GA to achieve better performance than all the existing ones.
In most existing hybrid algorithms of GA and BA, two individual subpopulations are controlled by GA and BA separately, and recombined periodically. However, it is difficult to recognize interactions between GA and BA because they are loosely coupled. For instance, it is hard to judge how individuals yielded from GA affect BA population,and how individuals from BA survive in GA population. To address this challenge, we design a self-adaptive bat algorithm with genetic operations (SBAGO) that incorporates GA’s genetic operations into BA. This work aims to make the following innovative contributions:
1) It combines GA and BA together in a highly integrated way, thus leading to a new BA and GA hybrid method called SBAGO. GA produces exemplars with its genetic operations for bats in BA while BA updates its bats by both its best solution and the exemplars from GA. In addition, survived exemplars in GA are diversified with high-quality because of genetic operations. Therefore, they improve BA’s search efficiency and avoid its premature convergence.
2) It passes promising and high-quality genetic information from BA’s search processes back to GA. Therefore, they help GA yield improved exemplars. It well uses such interactions between GA and BA to improve them in an alternate manner in SBAGO.
The rest of this paper is organized as follows. Section II discusses the algorithmic and biological backgrounds. Section III describes the implementation of SBAGO. Section IV presents the setting of experiments and gives the experimental results of SBAGO and recently proposed peers. Section V concludes this work.
II. BACKGROUND
A. Algorithmic Comparison: GA Versus BA
Both GA and BA are bio-inspired algorithms that have been applied to solve various types of optimization problems. The standard GA includes three major operations, i.e., crossover,mutation and selection. The selection operation chooses highquality individuals to breed offspring ones for increasing the fitness of the entire population. The crossover and mutation operations reproduce new offspring individuals, and the population evolves by using the genetic information of selected individuals. On the other hand, all bats in the standard BA adopt their echolocation behaviors to specify distance, and evaluate the distance variation between their prey/food and locations. Each bat randomly flies by following a velocity at a specific position with dynamic wavelength, loudness and frequency to find their prey. All bats dynamically change their frequencies or wavelength and update their pulse emission rates according to the proximity of their preys. BA does not adopt any selection operation, and its evolution is mainly realized by guiding bats towards the currently best positions.The flying processes of bats correspond to the transmission ones of genetic information in GA.
GA and BA differ considerably in terms of their convergence behaviors. The standard GA selects two random individuals to share their genetic information with a crossover operation. Then, GA further randomly changes some genes in the produced offspring individuals with a mutation operation.Consequently, the search process of GA is highly random and tends to be slow. On the contrary, bats in the standard BA move towards the best solution of all bats in the current population. Thus, the search process of BA is directional. As a result, BA shows quicker convergence and but worse global ability of solution exploration than GA.
It has been shown that BA can efficiently converge to the best solutions for unimodal functions because of its efficient search ability and high search accuracy [28]. On the other hand, BA is often trapped into a locally best solution for multimodal functions if the currently obtained solution falls into local optima and fails to jump out of them. Thus, its performance is poor when it has been used to solve multimodal problems. On the other hand, GA has superior a global search capability and a higher chance to find the global optima of multimodal functions than BA. Nevertheless, its evolution is slow because its crossover and mutation operations are time-consuming and highly random due to its directionless searches in solution space. Consequently, GA converges to the best solutions slowly, and its performance for unimodal,multimodal and complicated composite functions is not acceptable in many cases.
In summary, both GA and BA have their own advantages and disadvantages. Can we properly combine them to achieve better performance than them alone and their recent hybrid algorithms? This work intends to answer it.
B. Biological Comparison: Gene–Behavior Interaction
GA has been proposed to update the phenotype information of each individual in a biological manner by dynamically updating such information. Then, its population evolves through the update of all individuals. Alternatively, a BA updates the phenotype information of bats by learning from its locally and globally best solutions obtained so far, and its convergence is faster than a GA’s. According to [29], behavioral characteristics of individuals in nature are controlled by the genetic information. It is a commonsense that the genotype information and a living environment affect most behaviors of individuals [30]. For example, it has been shown that genotype information controls migration behaviors and directions of blackcap [31]. In addition, foraging behaviors of animals can be well analyzed by their evolutionary processes and genotypic differences, rather than the current foraging environments [32].
According to [32], individuals’ learning leads to their evolutionary results. The abilities obtained by them in real-life environments cannot be directly reflected in the corresponding genes. However, the phenotype differences among individuals greatly affect the selection in nature performed on them, and then change genes in the subsequent population in the evolution of generations. For example, some types of woodpeckers start to adopt the corresponding cactus spines to efficiently search food/prey in trees [33]. The selection in nature inclines to maintain some individuals with a beak shape of the current population, which can better adopt spines. In this way, more offspring woodpeckers inherit and own the ability of such beak shapes, and obtain such skill of feeding.Thus, the genotype information controls behaviors and the phenotype information of individuals. Meanwhile, GA selects individuals with some superior skills obtained by learning in real-life environments to breed with high probability. In this way, they transmit their genotype information to their offsprings.
To summarize, the interaction between genes and behaviors of individuals is beneficial to improve the future individual diversity in a population. Similarly, BA belongs a type of nature-inspired and meta-heuristic optimization algorithms. Its search process can be improved by adding some genetic operations into its learning process. This motivates this work.
III. GENETIC OPERATION-BASED BA
A. Original BA and Its Variants
In BA, the locally best position for each particleimeans its best solution obtained so far. The global optimum means the currently obtained best solution of the whole population. Each bat adjusts its position and velocity by using information from its locally best position, and a global optimum in the current population as obtained so far. LetMdenote the number of bats in the current population.videnotes the velocity of bati(1 ≤i≤M).xidenotes a position of bati.piandgdenote the locally best position of batiand a globally best one of all bats.LetDdenote the dimension of the vector representing the position of a bat. Letvi,dandxi,ddenote the values of each elementd(d∈{1,2,...,D} ) of vectorsviandxi, respectively.Letgddenote thedth element of vectorg. Letfidenote the pulse frequency of bati. For each elementd(1 ≤d≤D),xi,dandvi,dare updated as
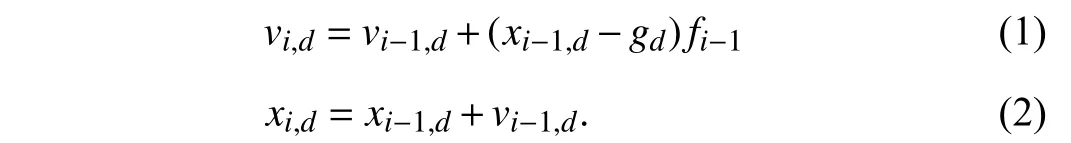
The minimum and maximum frequencies of each bat are denoted byandrespectively. Let βi∈ denote a uniformly distributed random number in [0, 1] for bati. Specifically,according to [15],fiis updated as
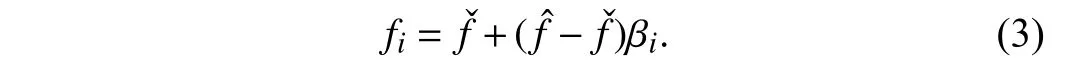
It is worth noting that each bat is guided by bothgandpi,and thus, it might oscillate dramatically if they are located in opposite directions ofxi. On the contrary, bats might trap into local optima ifpiandgare almost the same, thus leading to premature convergence. To address this issue, we propose a new hybrid algorithm that combines BA and GA next.
B. Self-Adaptive Bat Algorithm With Genetic Operations(SBAGO)
It is clear that each exemplarEifor batidetermines the search directions of the latter. Thus, these exemplars significantly affect BA’s search performance. This work integrates the genetic operations of GA into BA such that GA can produce high-diversity and high-quality exemplars for bats. In other words, we intend to use the outstanding global search capability of GA to benefit BA. Consequently, we intend to enhance the diversity of bats with the genetic operations of GA, and thus, avoid the premature convergence of BA. Note that the foraging behaviors of bats by the biological nature are beneficial to the high diversity and continuous survival of bats.
LetEidenote the exemplar for bati, and it is a composite exemplar that is a linear combination ofpiandg. LetEi,ddenote thedth entry ofEi. Thus
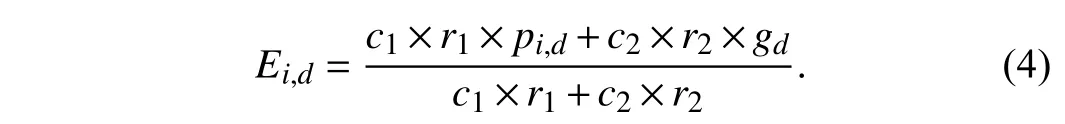
wherec1andc2are cognitive and social acceleration parameters to reflect the effects ofpi,dandgd, respectively in evolution, andr1,r2∈U(0,1).
In generationtof the while loop, there are four major parts,i.e., crossover, mutation, and selection operations for the update of exemplars and bat positions.
1)Crossover:For elementdof bati, the following crossover operation is performed. At first, batk,k∈{1,2,...,M},is randomly selected. Then, the operation of the crossover is applied togandpito produceOi= [Oi,1,Oi,2,...,Oi,D].Specifically
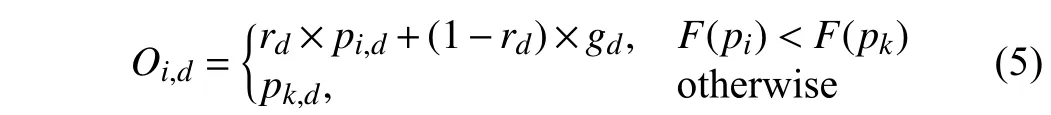
whererd∈U(0,1).
In this way, a crossover operation between a global optimumgand its local optimumpiof batican improve quality ofOi. However, if batiis an individual inferior to the others in the population,Oishould use more entries frompkof a randomly selected batkwith a higher value of fitness.The random selection of two bats in the current population for performing a crossover operation in GA. Our proposed crossover operation adopts previous search experiences of bats to enhance gene quality, thus improving search efficiency.
2)Mutation:This operation is applied toOiwith a probability denoted byζ. For each elementd, ifrd<ζ,Oi,dis changed with a uniformly distributed random number in(,), i.e.,
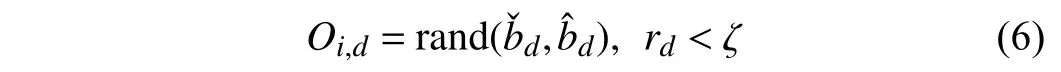
We adopt this operation to increase the diversity of exemplars. Note that any exploratory coordinates in solution spaces can be reached in the theory.
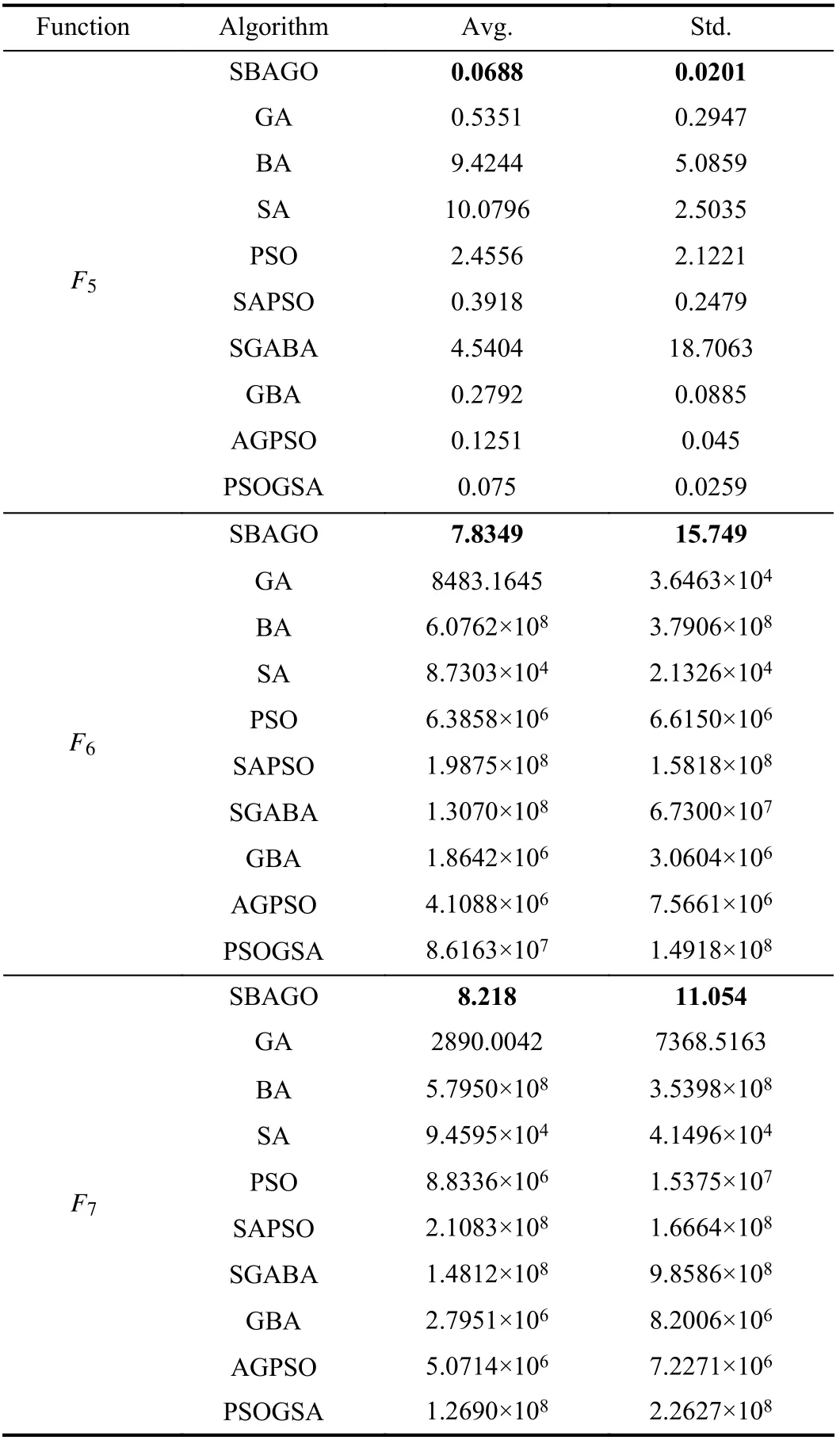
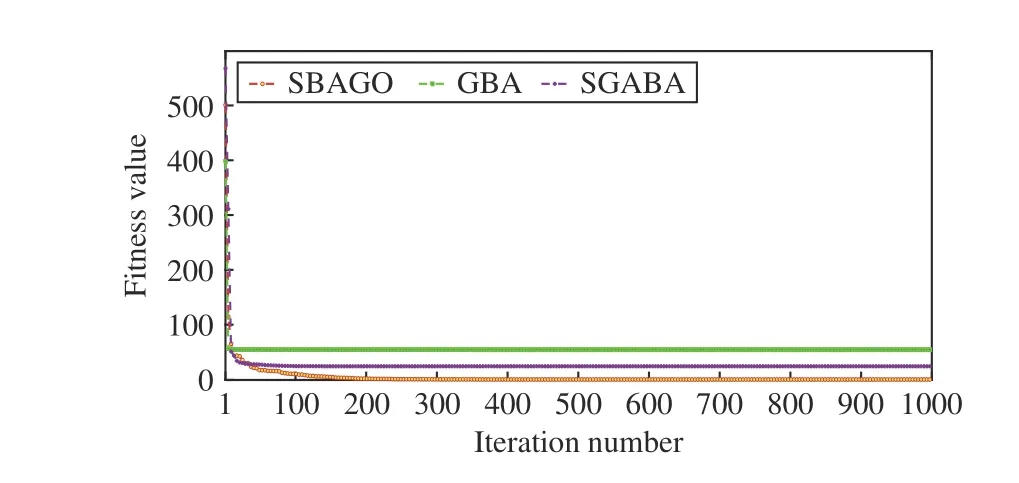
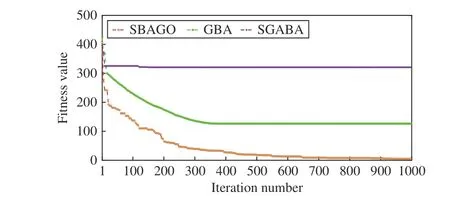
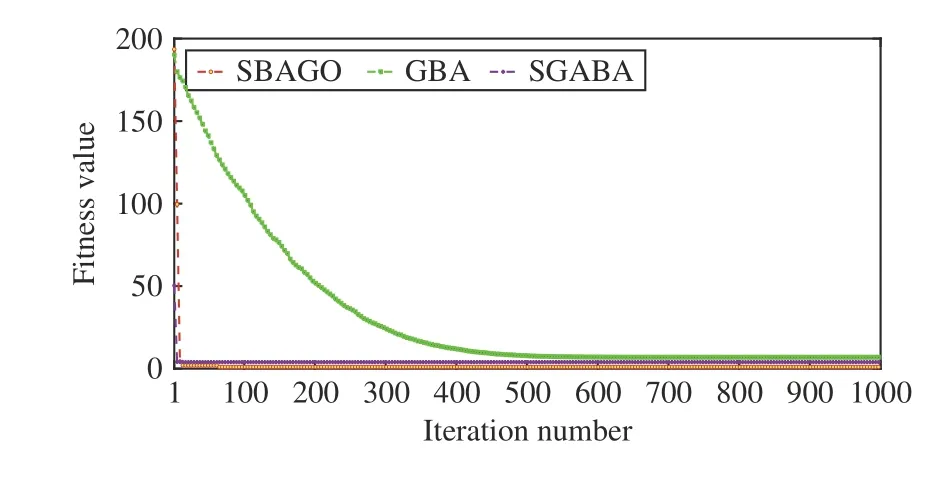
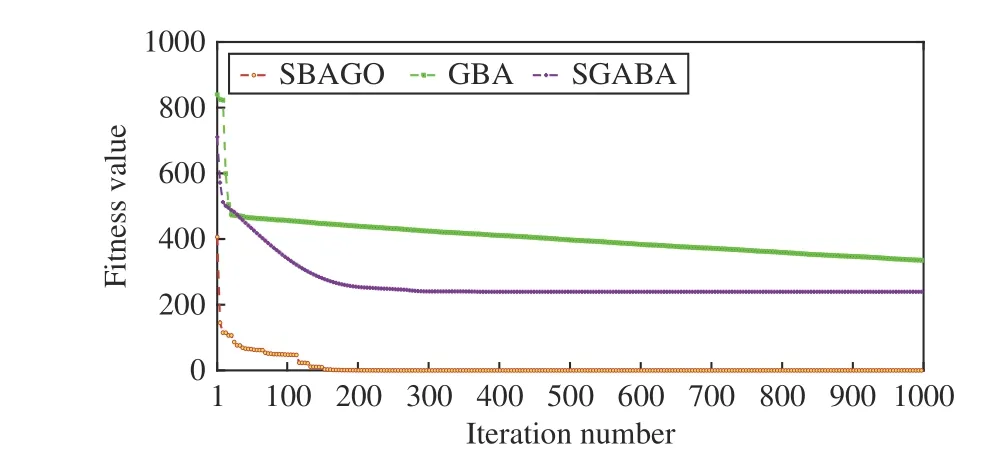
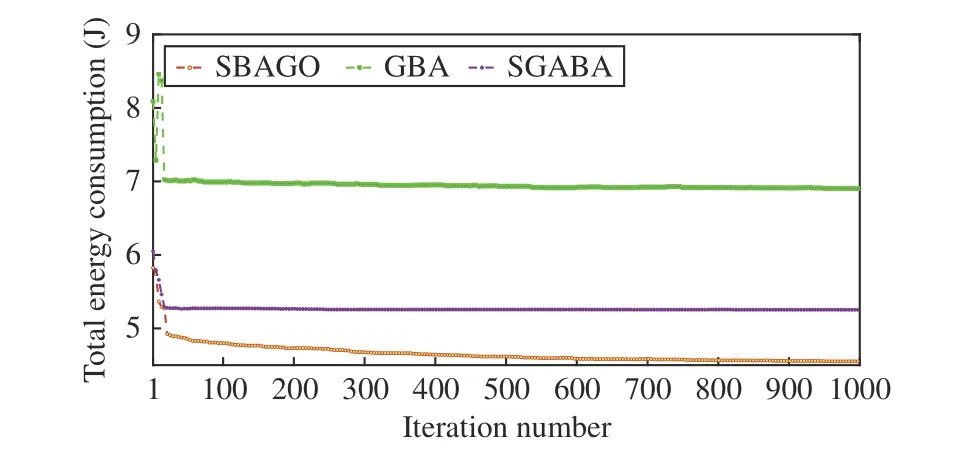
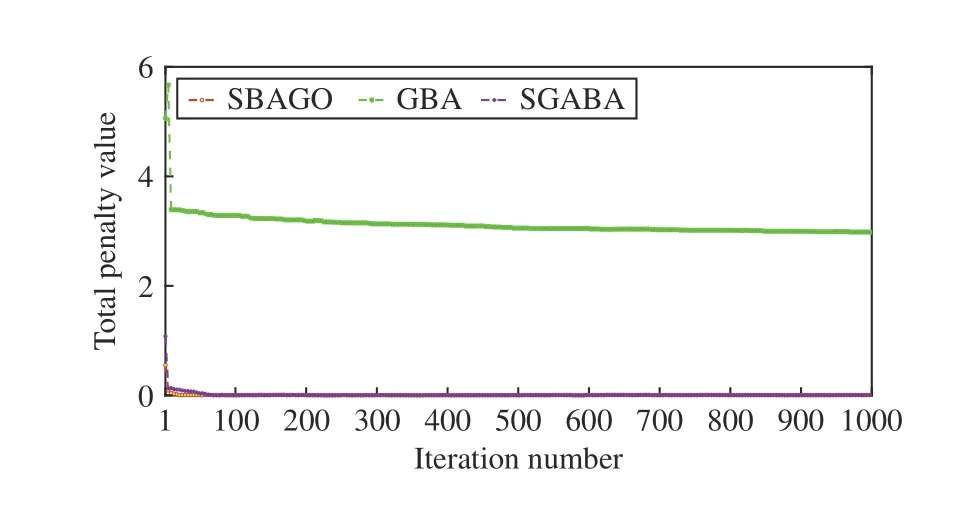
3)Selection:After crossover and mutation operations, we apply the one to specify whetherOiis selected to updateEi.Specifically, ifF(Oi) 4)Update of Bat Positions:tˆ denotes the total number of iterations in SBAGO. ωtdenotes the inertia weight in iterationt(1 ≤t≤tˆ ). ωtlinearly decreases from its maximum valueto its minimum value Letcdenote an acceleration coefficient reflecting the relative importance of the difference betweenxi,dandEi,d. Then,to avoid the premature convergence to local optima,vi,dandxi,dare updated as To mitigate the risk of the early convergence to local optima and increase the diversity of solutions, we perform the following local search, i.e., In each iteration, SBAGO adjusts the loudness and the rate of pulse emission for each single bat according to where ηiis the pulse emission rate of bati,Aiis the loudness of bati, andα( 0<α<1) andγ( 0<γ<1) are two coefficients. In real-life cases, if each bat finds its prey/food, its loudness reduces and its rate of pulse emission grows with the hope that bats move towards the global optima. Algorithm 1 implements SBAGO.F(xi) denotes the objective function value of bati. Line 2 randomly initializesviandxi, and evaluatesF(xi) accordingly. Line 3 randomly initializesfi, ηiandAifor bati. Line 4 updatespiwithxifor each bati. Line 6 setsgto the currently best position of all bats.Line 7 initializesEi,dwith (4) and updatesωwith (7). In iterationtof the while loop, crossover, mutation, and selection operations, and bat position update are performed for each bati. Lines 12–19 apply the operation of crossover forxi,d. Lines 21–25 apply the operation of mutation forxi,d. Lines 27–34 apply the selection forxi,d. Line 36 updatesfifor each batiwith (3). Line 38 updatesvi,dwith (8). Line 39 updatesxi,dwith (9). Lines 41 and 42 select a solution (x˜) among the best solutions currently obtained, and then updatexi,dif rand(0,1)>ηi. Then, Lines 47 and 48 updateAiand ηiifF(xi) Algorithm 1 SBAGO SBAGO mainly consists of three parts including initialization in Lines 1–8, genetic operations in Lines 12–34, and BA procedure in Lines 36–50. The complexity of Line 2 is 3Dand that of Line 7 is 3D. Thus, the complexity of initialization isD(4M+1). Let ϖGdenote the complexity of genetic operations for batiin each iteration. Let ϖBdenote the complexity of BA for batiin each iteration. So are those of Lines 12–19,Lines 21–25, and Line 27. The complexity of Lines 28–30 isD. The complexity of Lines 31–34 is ξM+D. Thus,ϖG=5D+ξM. The complexity of Lines 36–50 is 6D, i.e.,ϖB=6D. Thus, the complexity of SBAGO isD(4M+1)+(ϖG+ϖB)Mtˆ,i.e.,D(4M+1)+(11D+ξM)Mtˆ.Hence,its complexityisO(ξM2tˆ),whichismainlydeterminedby genetic operations of SBAGO. However, its complexity is lower than other algorithms [17], [35], [36] that integrate genetic operations into BA. The reason is that they use typical crossover operations, e.g., simulated binary crossover, partiallymapped crossover,K-point crossover, shuffle crossover, and cycle crossover, which require more iterations. They also adopt roulette wheel selection. To evaluate the performance of SBAGO, we adopt four types of widely used test suites including total 29 benchmark functions, which are adopted by many researchers [37]. In addition, we apply SBAGO to solve a real-life optimization problem in mobile edge computing systems [38]. A list of these functions and the details are given in Tables I–III in the Supplementary File (in the online version of this paper).Dmeans the number of decision variables, Range shows the boundaries of the solution space of each function, andmeans the minimum of a function. InF11(x) andF12(x),u(xi,a,k,m)is calculated as follows: This section groups these benchmark functions into multiple groups including unimodal, multimodal, fixed-dimension multimodal, and composite functions, which are given in Table I.The first test suite (F1–F7) consists of all the scalable functions widely tested in [39]. For example,F6is a base function named Elliptic and seen in many continuous optimization test suites [40], [41].F7is a large-scale shifted Elliptic function that is unimodal, fully-separable, shifted, smooth, illconditioned and has local irregularities. The second suite (F8–F13) includes multimodal functions with different shapes. For example,F13is a large-scale shifted Rastrigin’s function,which is multimodal, fully-separable, shifted, smooth, illconditioned and has local irregularities. The third suite (F14–F23) consists of fixed-dimension multimodal benchmark functions [42]. The last test suite (F24–F29) consists of six composite functions that are composite variants of typical benchmark functions. TABLE I UNIMODAL BENCHMARK FUNCTIONS (F1–F7) We execute SBAGO for 30 times on each function. Tables II and III show the statistical results ofF1–F7with respect to the average and standard deviations. Tables IV–VII in the Supplementary File give the statistical results ofF8–F29in the Supplementary File. We then verify and compare the efficiency and effectiveness of SBAGO with GA [43], BA [44], simulated annealing (SA) [45], [46], SA-based particle swarm optimization (SAPSO) [47], and particle swarm optimization(PSO) [48], [49], autonomous groups PSO (AGPSO) [50],hybrid PSO and gravitational search algorithm (PSOGSA)[35], genetic bat algorithm (GBA) [36], and SGABA [17]. In addition, the GBA[36]firstadoptsGAtoinitializea population ofsolutions, and toobtain thebest solution (xg∗)by searchingthe solutionspace.Then,the GBAadopts BAto furthersearch aroundxg∗andfinallyyields afinal solution(x∗). It is worth noting that GA and BA are executed sequentially in the GBA, and they do not interact with each other in each iteration. SBAGO integrates GA and BA in a cohesive manner, and they affect each other in each iteration. Besides,the SGABA [17] adopts a smart inertia weight to balance its exploitation and exploration based on fitness values. It yields a new solution by combining the globally best solution and the best one in each iteration to strengthen the local search in (10).In addition, it adopts a beta distribution to produce βiin (3),and changes the frequency of each bat smartly. Differently from the SGABA, our proposed SBAGO designs novel crossover, mutation, and selection operations to yield a highquality exemplar for each bat in each iteration. The exemplars further guide the search process of bats in the population. The SAPSO is a hybrid algorithm combining the SA and the PSO. In it, each particle changes its position with the Metropolis acceptance rule of the SA. It compares a fitness value of each current particle and a newly produced one. It selects better particles directly and conditionally chooses worse ones with the objective of jumping from local optima and obtaining global ones. Specifically, the parameter setting of SBAGO is given as follows.M=20,=1000,Ai∈[1,2],ηi∈[1,2],=0,=0.9,δ=7,γ=0.9 ,α=0.9,ωˆ=1, ωˇ=0.74,ζ=0.02,c1=c2=0.5,c=1.1, ξ=0.2 and ϵ=0.001. All these algorithms are implemented in a computer with an Intel(R)Core(TM) i7 CPU 6600U at 2.60 GHz with 16 GB of RAM. TABLE II RESULTS OF UNIMODAL BENCHMARK FUNCTIONS (F1–F4) According to [42], unimodal functions can well benchmark the exploitation ability of meta-heuristic algorithms. Tables II and III show results with all ten tested algorithms. SBAGO provides very competitive results in comparison with its nine peers. It outperforms them in terms of average and standarddeviations in all functions (F1–F7) in the first test suite. Thus,SBAGO owns high exploitation ability. This is caused by the integration of the proposed crossover, mutation and selection operations into BA. Figs. 1 and 2 in the Supplementary File illustrate the 2D shapes, search histories, trajectories, fitness histories and convergence curves with SBAGO. For example,forF1, its first subfigure shows its 2D shape. The second and third ones show the search history of its first two dimensions,and the trajectory in the first dimension in each iteration,respectively. Its fourth and fifth subfigures show fitness history and convergence curve as iterations proceed, respectively. Note that the fitness history curve means the fitness value of the first bat, while the convergence curve gives the globally best fitness value as iterations proceed. TABLE III RESULTS OF UNIMODAL BENCHMARK FUNCTIONS (F5–F7) To verify the exploration ability of SBAGO, this work adoptsF8–F13, which consist of six multimodal functions.Differently from unimodal functions, multimodal ones own multiple local optima whose count increases exponentially with dimensions of optimization problems. They are suitable to evaluate the exploration ability of meta-heuristic algorithms. Table IV in the Supplementary File shows the results of ten algorithms. It is observed that SBAGO provides better results than its peers, i.e., it owns higher exploration ability than its peers. Fig. 1 in the Supplementary File shows 2D shapes, search histories, trajectories, fitness histories and convergence curves ofF7–F12with SBAGO. Tables V and VI in the Supplementary File show the results of fixed-dimension multimodal benchmark functionsF14–F23.SBAGO outperforms its peers in terms of the search ability.Figs. 3 and 4 in the Supplementary File show 2D shapes,search histories, trajectories, fitness histories and convergence curves ofF13–F23with SBAGO. To show the behaviors of SBAGO in the avoidance of local optima, we adopt the last test suit of benchmark functions[42]. They are composite ones and very difficult for metaheuristic algorithms. Here, we adopt six composite functions that have been widely used to evaluate performance of these algorithms to find the global optima [51]. Table III in the Supplementary File shows their details. For example,F24(x), combines ten simple functions, each of which is a sphere one [52]. These composite functions can well evaluate both exploitation and exploration of SBAGO. Importantly, they can evaluate the avoidance ability of local optima of metaheuristic algorithms because they contain many local optima.As shown in Table VII in the Supplementary File, SBAGO outperforms its peers on them. Fig. 5 in the Supplementary File shows 2D shapes, search histories, trajectories, fitness histories and convergence curves ofF24–F29with SBAGO.The result proves that SBAGO well balances exploitation and exploration, and can well avoid the early trapping into local optima. This is due to its integration of genetic operations of GA into BA in an optimization process. Specially, GA produces excellent exemplars with its genetic operations for more diverse bats, and provides high search ability to BA for quickly finding the optima. Thus, SBAGO owns the great ability to escape from local optima to exploit and explore solution space. Following [53], significant changes are needed in the changes of individuals over beginning steps of optimization. It is helpful to guide a meta-heuristic algorithm to extensively explore solution spaces of optimization problems. However,these changes have to be small enough to strengthen and stress exploitation at final stages of optimization. To illustrate the convergence behavior of SBAGO, Figs. 1–5 in the Supplementary File present the trajectory and search history of the first bat in the first dimension (x1) ofx. For example, the second subfigure of Fig. 1 in the Supplementary File presents the history of each bat’s search. It is shown that bats of SBAGO extensively find high-quality areas of solution spaces and investigate the most promising ones. Besides, the third subfigure of Fig. 1 in the Supplementary File presents the trajectory of the first bat whose changes in the first dimension(x1) are given. Clearly, several significant changes exist in the beginning stage of iterations, which are reduced gradually as iterations proceed. According to [53], this convergence behavior guarantees that SBAGO finally converges to a highquality solution in solution spaces. Fig. 1. Fitness values of F3 and F8 with respect to α, γ, and ζ. We now present a sensitivity analysis of the main parameters of SBAGO. Here, we take a unimodal function (F3) and a multimodal one (F8) as examples, and investigate the sensitivity of SBAGO to two coefficients, i.e.,αandγ, and mutation probability (ζ). Fig. 1 shows fitness values ofF3andF8with respect toα,γ, andζ, where the horizontal axis shows parameter values and the vertical axis shows their corresponding fitness values. Specifically, in Fig. 1 (a), SBAGO is compared with α= 0.1, 0.2, ..., 0.9, respectively while keeping the other parameters unchanged as those presented in Section IV-A. As shown in Fig. 1(a), fitness values ofF3andF8vary with different settings ofα, and it is the least when α= 0.9. Similarly, as shown in Fig. 1(b), fitness values ofF3andF8vary with different settings ofγ, and it is the least when γ= 0.9. At last, as shown in Fig. 1(c), fitness values ofF3andF8vary with different settings ofζ, and it is the least whenζ=0.02. The results show that the results of SBAGO are dependent on different settings of these three main parameters. For example, a largerζperturbs a stable search of bats and leads to undesired convergence, whereas a smallerζfails to avoid premature convergence. When ζ= 0.02, SBAGO achieves satisfying search results for both unimodal and multimodal problems. To summarize, α = 0.9, γ = 0.9, and ζ = 0.02 are recommended in this work. Self-adaptation of these parameters to different problems should be an important research direction. This work analyzes the convergence curves of the proposed SBAGO, GBA and SGABA on some representative benchmark functions (e.g.,F2,F8,F14andF24), and a reallife optimization problem in mobile edge computing systems[38]. Figs. 2−5 show the convergence curves of SBAGO,GBA and SGABA onF2,F8,F14, andF24, respectively. GBA and SGABA are two representative algorithms that also combine GA and BA. It is worth noting thatF2,F8,F14andF24are selected from four types of test suites, and they can well demonstrate the convergence performance of SBAGO. It is shown that the fitness value of each of them with SBAGO is the least among SBAGO, GBA and SGABA. For example, forF24, the final fitness value of SBAGO is 8.88 × 10−6, which is much lower than that (3.35 × 102) of GBA, and that (2.39 ×102) of SGABA, respectively. In addition, the real-life optimization problem [38] aims to minimize the total energy consumption of all mobile devices and edge servers. The decision variables include the task offloading ratio, CPU speeds of mobile devices, the bandwidth allocation of network channels, and the data transmission power of mobile devices. The problem considers limits of response time of tasks, the maximum CPU running speeds,the maximum transmission power, the maximum energy of each mobile device, and the maximum resources of CPU and memories in edge servers. We integrate the constraints into a constrained mixed-integer nonlinear program, and its complexity of solutions is NP-hard. This problem has an issue of exponential explosion, and there are no polynomial-time algorithms. We adopt a penalty function method to handle the constraints, each of which is transformed into a positive penalty. Then, Fig. 6 shows the total energy consumption of SBAGO, the GBA and the SGABA when they are adopted to solve the real-life optimization problem, respectively. It is shown that the total energy consumption of SBAGO is the least among three algorithms. Specifically, the final total energy consumption of SBAGO is 4.55 J, which is lower than that 6.90 J of the GBA, and that 5.52 J of the SGABA,respectively. In addition, SBAGO only needs 952 iterations to converge to its final fitness value while the GBA and the SGABA need 971 and 973 iterations to converge to their final ones, respectively. Furthermore, Fig. 7 shows the comparison of the total penalty values of SBAGO, the GBA and the SGABA, respectively. It is shown that the total penalty value of SBAGO is zero at the end of its search process, and this demonstrates that SBAGO yields a high-quality and close-tooptimal solution meeting all constraints of the real-life optimization problem. This is because GA yields promising and diversified exemplars for bats in BA, and BA updates its bats by learning the exemplars. In addition, bats transmit promising search information back to GA to yield improved exemplars. In this way, SBAGO improves the search efficiency of BA and avoids its premature convergence. Fig. 2. Convergence curves of SBAGO, GBA and SGABA on F 2. Fig. 3. Convergence curves of SBAGO, GBA and SGABA on F8. Fig. 4. Convergence curves of SBAGO, GBA and SGABA on F 14. Fig. 5. Convergence curves of SBAGO, GBA and SGABA on F 24. This work has proposed a self-adaptive bat algorithm with genetic operations (SBAGO). It well integrates the crossover,mutation, and selection operations of the genetic algorithm(GA) into the bat algorithm (BA) to produce exemplars to guide latter’s bats. SBAGO performs the genetic operations on historical search information of bats of BA to reproduce high-quality and diverse exemplars. SBAGO’s selection chooses high-quality bats to breed offspring ones, and uses crossover and mutation operations for the global exploration.Guided by the bred exemplars, the entire population evolves towards the global optima generation by generation. We conduct the experiments to evaluate the performance of SBAGO by using 29 benchmark functions in four test suites,and a real-life optimization problem from mobile edge computing. We compare SBAGO with nine meta-heuristic optimiza-tion algorithms including variants of GA, the simulated annealing, particle swarm optimization and BA. The experimental results show that SBAGO outperforms its peers in terms of global exploration, the local exploitation, and the local optima avoidance. Fig. 6. Total energy consumption of SBAGO, GBA and SGABA. Fig. 7. Total penalty values of SBAGO, GBA and SGABA. Our proposed SBAGO cannot well handle high-dimensional optimization problems, and its convergence speeds for solving them tend to be slow. Our future work aims to further extend it in the following directions. First, it is of interest to extend it to its multi-objective versions for high-dimensional constrained optimization problems [54], [55]. Second, we can adopt deep learning methods, e.g., stacked sparse auto-encoders, to capture distribution features of solutions obtained from the first several generations for guiding the search process of SBAGO in a more efficient manner. Third, we can apply it to more real-life optimization problems in other fields, e.g.,Internet of Things and image segmentation [38], [56]–[59].
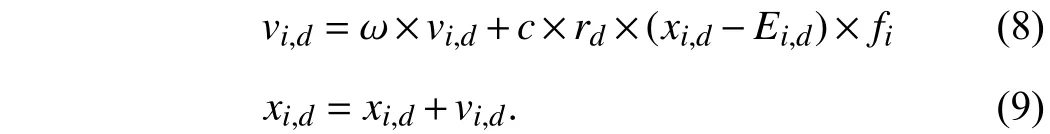
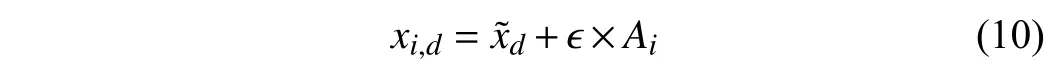
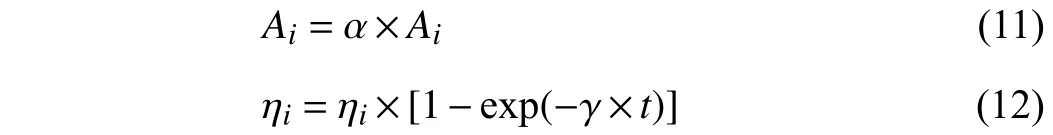

C. Complexity Analysis of SBAGO
IV. EXPERIMENTAL RESULTS AND DISCUSSION
A. Experimental Setup
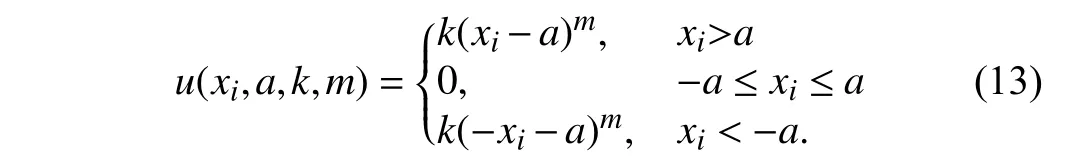

B. First Test Suite ( F1– F7)
C. Second Test Suite ( F8– F13)
D. Third Test Suite ( F14– F23)
E. Fourth Test Suite ( F24– F29)
F. Convergence Behavior Analysis

G. Sensitivity Analysis of Main SBAGO Parameters
H. Convergence Comparison of SBAGO, GBA and SGABA
V. CONCLUSIONS
 IEEE/CAA Journal of Automatica Sinica2022年7期
IEEE/CAA Journal of Automatica Sinica2022年7期
