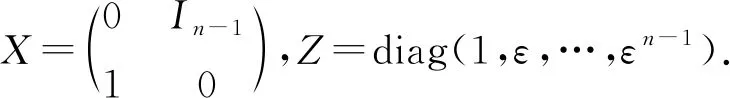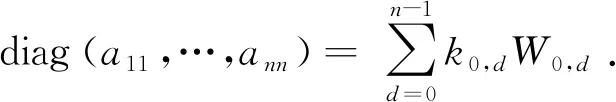关于广义Pauli矩阵的研究

任芳国， 申 明

(陕西师范大学 数学与统计学院，陕西 西安 710119)

作为一类重要的正规矩阵，酉矩阵具有良好的性质，在量子信息理论及控制理论中有重要应用，其中广义Pauli矩阵是一类重要的酉矩阵，它是解决量子信息问题的重要工具之一.Pauli矩阵是一种特殊的广义Pauli矩阵，文献[1]中指出量子力学中任意密度矩阵都可由Pauli矩阵表示，并为判断量子态为纯态或混合态提供了简便方法，文献[2—4]中给出了Pauli矩阵与量子逻辑门及量子运算之间的密切关系.同时，由广义Pauli矩阵构造出的Weyl信道在量子信息理论中扮演着重要角色.文献[5]给出了广义Pauli矩阵的部分性质和可用于构造MUBS的完备集，文献[6]通过广义Pauli矩阵构造出完全保迹映射，文献[7]中主要研究的广义Bell态与广义Pauli矩阵有密切联系.文献[8]研究了由广义Pauli矩阵构成的Pauli群的性质.基于此，本文从矩阵理论出发对广义Pauli矩阵进行深入研究.

1 符号说明与预备知识

1.1 符号说明

1.2 预备知识

定义1[1]Pauli矩阵是指4个常用矩阵：

定义2[1]称迹为1且为半正定的矩阵为密度矩阵.

定义3[9]设A∈Mn.若A*A=In，则称A是酉矩阵.

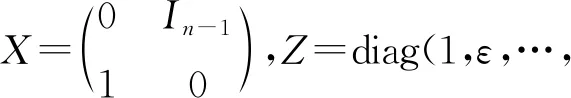
注1W0,0=Wn,n=In.

定义5Δ,Ω分别表示矩阵空间Mn上的两个变换:

Δ(A)=diag(a11,…,ann),∀A=(aij)n∈Mn;

引理1[1]设A,B是矩阵空间Mn上的任意两个矩阵，函数(A,B)=tr(A*B)是Mn上的一个内积函数.

2 主要结论

下面先讨论两个特殊的酉矩阵及其关系.

定理1设n是给定的正整数，令Z=diag(1,ε,…,εn-1)是n阶矩阵，其中ε为n次基本单位根，则下列结论成立：

(ⅲ)令GZ={In,Z,…,Zn-1}，GZ关于矩阵的普通乘法是n阶循环群；

(ⅴ)GZ={In,Z,…,Zn-1}是Mn中对角矩阵子空间的一组正交基；

(ⅵ)设∀A=(aij)n∈Mn，则

即Z是n阶酉矩阵，再由ε为n次单位根知Zn=diag(1,εn,…,εn(n-1))=In.∀k∈Z，由带余除法知存在整数q,r，使得k=nq+r，其中0≤r≤n-1，则由Z是酉矩阵及Zn=In可知Zk=Znq+r=ZnqZr=(Zn)qZr=Zr是酉矩阵.

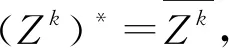
(ⅴ)显然GZ={In,Z,…,Zn-1}中元素全为对角酉矩阵且当0≤j,k≤n-1,j≠k时，0<|j-k|≤n-1.因此，由引理1可得

(Zj,Zk)=tr((Zj)*Zk)=tr(Z-jZk)=

从而GZ中元素两两正交，再由Mn中对角矩阵子空间的维数为n知GZ={In,Z,…,Zn-1}是Mn中对角矩阵子空间的一组正交基.

于是

diag(a11,…,ann).

综上所述，定理1证毕.

k

(ⅱ)GX={X0,X,…,Xn-1}是n阶酉群中的一个n阶循环子群.

(ⅵ)GX={In,X,…,Xn-1}是Mn中循环矩阵组成的子空间的一组正交基.

X2=X(en,e1,…,en-1)=

(Xen,Xe1,…,Xen-1)=(en-1,en,…,en-2)=

假设结论对k成立，即

现在讨论k+1的情况，由于

Xk+1=XXk=X(en-k+1,…,en,e1,…,en-k)=

(Xen-k+1,…,Xen,Xe1,…,Xen-k)=

(en-k,…,en-1,en,e1,…,en-k-1)=

(ⅱ)由X是酉矩阵及(ⅰ)知，∀m∈Z，由带余除法知，存在整数q,r，使得m=nq+r，其中0≤r≤n-1，则由X是酉矩阵及Xn=In可得Xm=Xnq+r=XnqXr=(Xn)qXr=Xr；∀s,t∈{0,1,…,n-1}，XsXt=Xs+t∈GX，(Xs)-1=(Xs)*=(X*)s=(Xn-1)s=Xs(n-1)∈GX.再由(ⅰ)知，对整数s,t，当0≤s,t≤n-1,s≠t时Xs≠Xt，则GX={X0,X,…,Xn-1}是n阶酉群中以X为生成元的n阶循环子群.

XkA(Xk)*=

则由(ⅳ)知

(ⅵ)GX={In,X,…,Xn-1}中元素全为非零循环矩阵，再由(ⅲ)知j,k∈{0,…,n-1}，

(Xj,Xk)=tr((Xj)*Xk)=

则(ⅵ)得证.

综上所述，定理2证毕.

(ⅰ)存在酉矩阵U∈Mn，使得X=U*ZU.

(ⅱ)XZ=εZX，XkZ=εkZXk,XZj=εjZjX，XkZj=εjkZjXk，其中j,k是任意给定的非负整数.

(ⅲ)XkZj=εjkZjXk，其中j,k是任意给定的整数.

(ⅳ)设j,k是任意给定的整数，则XkZj=In当且仅当n|k且n|j.

(ⅴ)设j,k是任意给定的整数，则XkZj是对角矩阵当且仅当n|k.

证明(ⅰ)由于fX(λ)=|λIn-X|=λn-1，X的特征值是全体n次单位根，再由酉矩阵是正规矩阵知，存在酉矩阵U∈Mn，使得X=U*ZU.

(ⅱ)由定理2(ⅴ)知XZX*=diag(ε,…,εn-1,1)=diag(ε,…,εn-1,εn)=εZ，再由X是酉矩阵知XZ=εZX；对k做数学归纳证明XkZ=εkZXk.如果k=0结论显然成立，下面只考虑k是正整数的情形. 由于X2Z=X(XZ)=X(εZX)=ε(XZ)X=ε2(ZX)X=ε2ZX2，假设XkZ=εkZXk，则

Xk+1Z=X(XkZ)=εkX(ZXk)=

εk(XZ)Xk=εk(εZX)Xk=εk+1ZXk+1，

所以XkZ=εkZX成立.同理可证对任意非负整数j,k，XZj=εjZjX，XkZj=εjkZjXk成立.

(ⅲ)由带余除法知，存在整数q1,q2,r,s，使得k=nq1+r，j=nq2+s，其中0≤r,s≤n-1，则由X,Z的周期都是n知XkZj=XrZs=εrsZsXr，再由ε的周期为n知

εrsZsXr=εrsεn(nq1q2+q2r+q1s)Znq2ZsXnq1Xr=

εrs+n(nq1q2+q2r+q1s)Znq2+sXnq1+r=εkjZjXk，

从而XkZj=εkjZjXk.

(ⅵ)充分性：由带余除法知，存在整数q1,q2,r,s，使得k=nq1+r，j=nq2+s，其中0≤r,s≤n-1，则由X,Z的周期都是n知XkZj=XrZs.

显然tr(XkZj)=0；

下面讨论广义Pauli矩阵的性质.

定理4(ⅰ)Wa,b是酉矩阵且

(ⅴ)集合{Wa,b|a,b∈Z}={Wa,b|a,b∈{0,1,…,n-1}}的势为n2.

(ⅵ){Wa,b|a,b∈{0,1,…,n-1}}是矩阵空间Mn的一组正交基.

证明(ⅰ)由于Xa,Zb都是酉矩阵，由酉矩阵关于乘法封闭知Wa,b是酉矩阵.由定理3知

ZbX-a=εabX-aZb=εabW-a,b，

Z-bX-a=ε-abX-aZ-b=ε-abW-a,-b.

(ⅲ)Wa,bWc,d=(XaZb)(XcZd)=Xa(ZbXc)Zd=

ε-bcXaXcZbZd=ε-bcXcXaZdZb=

εad-bcXcZdXaZb=εad-bcWc,dWa,b,

(ⅳ)设α是Wa,b的属于特征值eiθ(θ∈R)的特征向量，即Wa,bα=eiθα，那么

εad-bc(Wa,bα)*Wc,dWa,bα=

εad-bc(eiθα)*Wc,d(eiθα)=

εad-bce-iθeiθα*Wc,dα=εad-bcα*Wc,dα，

(ⅴ)由带余除法知，对任意的整数a,b，存在整数q1,q2,r,s，使得a=nq1+r，b=nq2+s，其中0≤r,s≤n-1，则由X,Z的周期都是n知

Wa,b=XaZb=Xnq1+rZnq2+s=Xnq1XrZnq2Zs=XrZs，

{Wa,b|a,b∈Z}={Wa,b|a,b∈{0,1,…,n-1}}.

下证∀a,b,c,d∈{0,1,…,n-1}，若(a,b)≠(c,d)，则Wa,b≠Wc,d.假设(a,b)≠(c,d)，但Wa,b=Wc,d，即XaZb=XcZd，于是Xa-c=Zd-b，由于Zd-b是对角矩阵，从而Xa-c是对角矩阵，因此Xa-c=In.于是由X的周期是n知n|(a-c)，此时由Zd-b=In及Z的周期是n知n|(b-d)，由(a,b)≠(c,d)知a≠c，b≠d至少有一个满足.不妨设a≠c，由a,c∈{0,1,…,n-1}可知0<|a-c|

(ⅵ)由定理3知

tr(Z-bX-aXcZd)=tr(Xc-aZd-b)=

再由Wa,b是酉矩阵显然非零及dim(Mn)=n2知{Wa,b|a,b∈{0,1,…,n-1}}是矩阵空间Mn的一组正交基.

注2①对广义Pauli矩阵Wa,b,若无特别说明，一般a,b∈{0,1,…,n-1}.

下面给出广义Pauli矩阵的一个应用.

定理5设A=(aij)n∈Mn，则

从而

所以(ⅰ)成立.

(ⅱ)由定理4(ⅲ)知

从而

即(ⅱ)成立.

(ⅲ)由定义5及(ⅰ)～(ⅱ)的证明即得.

综上所述，定理5得证.

注3设A=(aij)n∈Mn，则

①存在A的酉相似的凸组合为diag(a11,…,ann)；