Rasch 模型在初等教育阶段试卷质量分析领域的应用
李静璇,王秋红,何壮,袁淑莉
(1.贵阳学院 教育科学学院,贵州 贵阳 550005;2.贵阳市民族中学,贵州 贵阳 550025)
2021 年7 月,中共中央办公厅、国务院办公厅颁布的《进一步减轻义务教育阶段学生作业负担和校外培训负担》[1]文件中明确提出“提高作业设计质量”“提升课堂教学质量”等要求,以推动双减政策的实施,减轻义务教育阶段学生学业负担。
要“提高作业设计质量”“提升课堂教学质量”,就要做到对每次测验评价合理、对学生能力评估准确,才能避免无意义的机械重复作业设计和课堂教学。同时,还应根据学生的实际表现做到科学评价、精准反馈。
教育领域中,能力评估的工具多为试卷或量表。所谓量表是指具有确定测量单位和参照点的测量工具。因此教育测量中,按照标准化程序命制的试卷即是教育测量的一种量表[2]。由高水平量表或题目组成的题库是实现学生能力准确评估的基础。初等教育阶段严格限定教育考试的强度,因此,学校对教育测评的效率提出了更高的要求。高质量题库在中小学阶段显得更加珍贵。
高质量题目和试卷的筛选要对试卷难度、题目难度、学生能力等进行分析和比较,需要用到以Rasch 模型为代表的现代教育测量理论。Rasch模型可以将被试能力水平和试题难度转换为相同单位并放在同一把标尺上进行比较,能够真实客观地测量被试与试题的关系,在教育考试数据分析中具备独特的优势,故本研究拟使用Rasch 模型进行初等教育阶段试卷质量分析。
一、研究现状评述
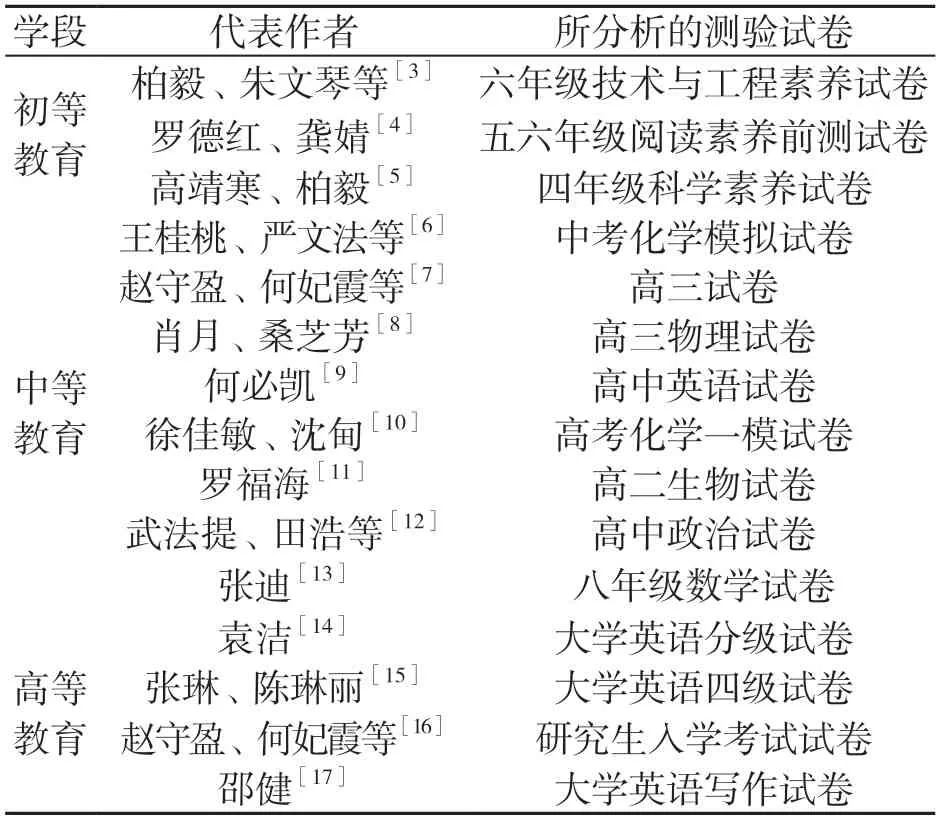
表1 不同阶段的相关文献
将有关Rasch 模型在试卷质量分析领域文献的作者和学段进行汇总分析,可以发现运用Rasch模型进行试卷质量分析最多的是中等教育阶段,其次是高等教育阶段。Rasch 模型在我国初等教育的应用研究最少,模型应用尚存巨大的发展空间。
二、方法与工具
(一)研究对象
以小学六年级数学考试成绩数据为研究对象,共收集325 名学生的成绩,根据教育测评的非速度型假设,删除2 名未答完试卷学生,有效数据323 名。
(二)研究工具
本次测验试卷共有29 道题,分为客观题和主观题。其中客观题共19 道分别为选择题和判断题,主观题共9 道大题包括计算题、操作题和应用题,其中每道大题分别包括2~8 个小题,各题型所对应的题目如表2。

表2 试卷题型说明
(三)数据分析
运用SPSS21.0 对数据进行分析以及单维性检验,运用Rasch 模型的分析软件Facets 对数据进行参数估计,包括试题难度、被试能力水平、数据与模型拟合值、主观题的阈值参数等。
三、结果与分析
(一)单维性检验
单维性是Rasch 模型分析的前提条件,在本次研究中,单维性是指测评过程学生的数学能力特质对其作答表现起决定作用。即便存在部分能力对评价结果产生影响,这种影响也不是决定性的。对数据单维性的检验可以通过原始数据的主成分分析、模型分析的残差分析等多种方法实现。
本次测验试卷的主成分分析结果如表3。使用该方法对原始数据进行单维性检验时,如果主成分数量为多个,则要求第一主成分特征根与第二主成分特征根的比值大于或接近3 且第一主成分解释率要大于20 %[18]42。数据显示KMO 和Bartlett 球形度检验结果均满足相关学者建议的标准,可以进行主成分分析。测验的主成分数量为9个,第一主成分解释率大于20%,但第一主成分特征根与第二主成分特征根的比值为2.909。

表3 原始数据主成分分析
对Rasch 模型分析的残差进行主成分分析,结果如表4。测量解释方差的比例为96.04 %,远远高于所要求的40 %[18]44,说明测试满足单维性假设。

表4 残差主成分分析
(二)怀特图分析
Rasch 模型可以通过对数转换将被试能力水平与试题难度之间的关系分布情况放在同一单位为“Logit”的标尺上进行比较和分析。这个表示被试能力与试题难度之间关系的图叫作怀特图(如图1 所示),一般用于对试卷的测量学特点的分析。位于中间的竖线叫作Logit 量尺,它是比较被试能力与试题难度的统一量尺,图中的一个“*”表示9 名被试,一个“·”表示8 名及以下被试,Measr(即Measure)对应的是量尺的“Logit”数值,Students 对应的是被试能力水平分布,Item对应的是试题难度分布。Logit 刻度尺从上往下,相对应被试的能力水平逐渐降低,试题的难度也逐渐减小,刻度尺的0 点为所有试题的平均难度。被试与被试间的间隔表示不同被试间能力水平的差异,试题与试题的间隔表示不同试题间难度的差异,距离越远,差异越大;反之,则越小。如果被试能力与试题难度越接近,那测验所获得的被试信息量越大,对被试能力水平的估计就越精确[19]。Rasch 模型中,当题目难度与被试能力相等时,被试答对该题的概率为50%,随着被试能力的提高,其答对该题的概率也将逐渐增加。
从图1 被试能力水平和试题难度的分布来看,被试能力分布集中在[1,5]之间,呈负偏态分布;试题难度分布集中在[-2,1.5]之间,呈正偏态分布。被试能力水平的平均值为3.4 左右,试题难度的平均值为0,所有试题中O16 最难,只有能力在5.86 的被试才有较高概率答对,O04、O02、O01 这几道题最简单,所有被试都有较高概率答对。结合图1 和各题目的得分率、正确率,整套测验试卷的难度对于被试来说略低,高难度的试题较少,且能力水平分布在[1.6,4.27]之间的被试,没有与之能力相匹配的试题。这部分学生,除难度最大的O16 之外,他们有可能答对所有题目。难度最大的O16 的难度值为4.57,部分被试能力达到了5.86,对于他们而言有可能答对所有试题。题目简单,导致本次考试出现了“天花板效应”。

图1 怀特图
(三)题目特点分析
对测验试卷的整体检测,使本研究对测验试卷的质量有了初步的了解,但这只是从宏观层面来判断试卷质量,并未具体到各道试题。一份测验试卷质量的高低是由组成该试卷的各试题共同决定的,因此,还需深入到具体试题,明确质量偏低的试题,进行原因分析,选择优化策略,作出调整,以提高测验试卷的整体质量。
表5 为此次试卷所有试题的基本参数。其中Measure 表示试题的难度;Model S.E.即Rasch模型标准误,指试题难度估计误差;Infit MNSQ指的是原始数据与Rasch 模型的拟合值;Coor.PtBis 是相关系数,即试题与试卷测量目标(总分)的相关,系数越高,试题与试卷测量目标越相近,试题对测量的贡献越大。

表5 题目参数估计结果
试卷的所有试题Infit MNSQ 的数值均在[0.5,1.5]之间,达到了相关学者建议的范围,表明数据与模型之间的拟合度良好。Rasch 模型标准误的大小直接影响了参数估计的稳定程度,误差越大,估计的结果越不稳定。从表3 中得出,S2021、S23、S24、S25、S27 和S29 这 几 道题 的标准误都小于0.1,表明这几道试题在估计被试能力水平时较稳定,O01、O02 和O04 这三道题的标准误是所有试题中最大的,均在0.5 以上,表明在整套试卷中这三道题在估计被试能力水平时最不稳定。图1 显示这三道题是所有试题中难度最低的,没有能力与之相匹配的被试,即所有被试均有可能答对,出现了“天花板效应”,因此,很难对题目参数作准确估计。观察各题的相关系数可以发现,O05、O06、O15、O16、O17、O18 这几个试题的相关系数较低(均低于0.2),表明这几道题与试卷测量目标关联度不高,对本次测量的贡献较小,除此之外,其余试题的相关系数均处于可接受的范围内。
四、对策与建议
(一)测验试题改进对策
1.提高试题整体难度
上述分析表明,试卷的整体难度低于被试能力水平,而且试题分布也没有覆盖不同能力水平的被试,这会影响测量结果的准确性。对此,在接下来试卷质量优化的过程中,可以适当删减难度较低的试题,或者提升这部分试题考查的认知能力,以提高试题或试卷的总体难度。
2.合理分配试题数量
数学的课程内容包括了数与代数、图形与几何、统计与概率、综合与实践四部分,测验试卷的编制也覆盖了这四个内容,但是在试题数量的分配上综合与实践部分仅有两题。对于不同层次认知能力方面的试题分配也主要集中在应用层次,对知识点掌握要求更高的分析层次较少。
分析层次要求被试将所提供的试题信息进行再组织,弄清信息间的关系以及构成这些信息的基础知识,以这些知识为基础进行分析,从而得出结论。这是本次考试被试得分率最低的部分,理应加强被试分析能力的训练,但是由于试题较少,无法准确判断被试是因为分析能力较差还是对基础知识掌握不到位导致失分,所以应当增加针对这一内容的试题,以便作出正确判断。
3.提高试卷区分度
整套试卷部分试题的相关系数不太理想,O05、O06、O15、O16、O17、O18 这几道试题的相关系数均低于相关学者建议的范围。这代表试卷和试题区分度不高,对测量的贡献较低。在改进过程中,应参考怀特图,调整题目内容和难度分布,提高试卷区分不同能力水平学生的能力,使试卷整体难度适中,增强试题与测量目标之间的关系。
(二)学生学业评价建议
1.积累评价数据建立高质量题库
对学生能力的准确评估需要以高质量题库为基础。教育信息化的发展,阅卷系统、教育考试数据分析软件等的普及为建设高质量题库提供了条件。学校应当发挥教育信息化的优势,以Rasch模型为指导,不断积累高质量题目资源,形成题库,为学生能力评价提供支持。
2.量化与质性相结合
教育评价要从侧重量化评价转向量化、质性相结合。对于学生学业成就的评价不应只是单纯地呈现量化结果,还应伴随有关学生的进步情况、掌握情况、能力情况、学习不足等质性的评价,这样将更有利于促进学生的发展。Rasch 模型可以直观地展现学生能力及其变化的情况,在未来的成绩报告中,教师应当用好怀特图,结合双向细目表,作好成绩的分析及反馈。
(三)教师教学实施建议
1.试卷点评兼顾及时性和针对性
测验结束后,教师应当及时对知识点进行点评、讲解,同时注意以数据分析结果为依据,切忌一讲到底。因此,试卷点评应当在取得考试数据分析报告之后,针对数据中反映出的问题,有所取舍。
2.试卷讲解注重全面性和特殊性
对于试卷中的易错题、难度较大的题,教师在讲解时应考虑到不同能力水平的学生,因材施教。对于学生在测验中普遍存在的问题,教师要针对这些问题从题目难度、考查知识点、失分原因等多方面进行深度分析,帮助学生理解相应的知识点,提高能力。对重点关注的学生,应当基于其个人数据,在不占用课堂时间的前提下作个别辅导。
3.教学实施注重学生双基的训练
对基础知识和基本技能的学习和把握是促进学生发展的基础,教学活动要让学生获得基础性发展。Rasch 模型对题目特征的分析,为题目所考查的知识和技能培养提供了重要线索。教师在实施教学时应当在知识和能力掌握难度适度的基础上,开展合理的教学和训练。杜绝无数据依据的机械刷题训练、题海战术。
4.教学实施注重多样化组织形式
教师在实施教学活动时可根据评价结果调整教学内容及其组织形式。统一教学是传统教学模式下最常见的组织形式,适用于知识、能力的初步学习和训练。但在开展测评并获得学生知识掌握和能力发展状态之后,可根据实际情况选择不同的教学方式,如个别辅导、分组教学、翻转课堂,预习或课后复习等。
教育大数据的技术与方法是提高教育评价质量的重要抓手,是实施教育评价改革的主要举措之一。以Rasch 模型为代表的现代教育测量理论在教育数据挖掘中体现了独特的优势,应当在实践中不断发展和普及。

