基于NAR邻近基坑开挖建筑位移预测模型

安 月,宁 欣,芮勇勤

(1.东北大学 资源与土木工程学院,辽宁 沈阳 110819;2.东北财经大学 投资工程管理学院,辽宁 大连 116025)

基坑开挖施工会导致土体卸荷,邻近地表、建筑受侧向土压力作用,向基坑开挖方向倾移。变形过大不仅影响建筑安全,甚至造成更大的人身、财产损失[1]。建筑竖向位移能够表征建筑由于基坑开挖施工引起的稳定性变化,是评估建筑安全的有效指标[2]。因此,能够准确预测建筑竖向位移值,及时采取相应的有效控制措施是保证建筑安全的关键[3,4]。

对于此类工程变形的预测问题,神经网络突破了普通数学模型的不足和有限元模型的低效,特别适用于具有强非线性的位移变化预测研究,使预测过程更高效、更准确[5,6]。李昂[7]、孟江[8]等采用BP(Back Propagation)模型对邻近基坑开挖桥墩的变形进行预测研究,表明BP对短期与中长期位移预测结果都具有很好的适用性。郑秋怡等[9]建立基于LSTM(Long Short-Term Memory)大跨拱桥的温度-位移预测模型,考虑位移时滞效应和非线性,降低预测误差。因为建筑位移变形常受基坑开挖施工、架设支撑、注浆加固等多种因素影响,变形规律分布具有非线性、时序动态性[10]。经过学者进一步研究表明,BP，LSTM神经网络对于动态问题的预测往往存在一定误差[11]。而NAR(Nonlinear Auto Regressive)模型兼具时间序列回归模型和非线性动态神经网络的优点,非常适合结构复杂的非线性、时变系统的时间序列预测问题。黄慧[12]、Cheng[13]等将NAR神经网络模型应用于动态非线性问题研究,Sunayana,Farhan Mohammad Khan[14,15]基于NAR神经网络进行时间序列预测模型的研究,表明NAR对动态非线性时序预测问题具有很好的精准性及适用性。NAR神经网络日益在工程风险预测领域中的非线性动态预测问题中应用广泛[16]。部分学者将NAR动态神经网络应用于隧洞围岩变形、桥梁结构的应变、大坝变形、基坑位移等预测模型研究,比较分析预测值与实测值,通过平均绝对方差和平均相对方差验证模型精度,结果表明NAR预测模型具有泛化性能好、精度高的优势[18]。因此NAR神经网络具有高度自学习和自适应能力,是建立建筑位移预测模型的有效方法[19]。

当前对基坑开挖引起的建筑变形研究主要是直接采用建筑的历史监测数据进行预测模型研究。然而基坑开挖施工具有灾害连锁反应关系,且地表塌陷与建筑物坍塌有直接传递关系[20]。尚缺乏通过地表沉降与建筑位移的非线性相关性进行建筑位移预测模型研究,此模型能够减少时滞效应带来的误差。本文以具有时序动态性能的NAR神经网络模型为基础,基于施工现场的实际监测数据,建立地表-建筑位移预测模型。经过多轮参数优化,训练高预测精度模型。以某基坑开挖邻近地表、建筑位移实测数据进行预测模型研究,利用地表沉降数据动态地实时预测邻近建筑沉降,并根据其预测结果判断预警程度,为保持基坑开挖施工过程中建筑稳定性提供理论保障。

1 NAR神经网络原理及步骤

1.1 NAR神经网络原理

NAR神经网络是一种用于描述非线性动态递归神经网络[21]。其表达式见式(1)。

y(t)=f{r(t-Du),…,r(t-1),r(t),c(t-Dc),…,c(t-1)}

(1)

式中：f( )为训练拟合的非线性函数；r(t),c(t)为t时刻的输入与输出；Du,Dc为输入与输出时延最大阶数；r(t-Du),…,r(t-1)、c(t-Dc),…,c(t-1)为相对t时刻的历史输入、输出。

NAR动态神经网络具有输入层、输出层、隐含层与输入与输出的延时。NAR网络通过加入延时和反馈机制增加网络模型对历史数据的记忆能力,以历史状态值预测下一时刻的状态值,适用于时间序列预测分析,被广泛应用于非线性动态序列预测研究,其结构模型见图1。

图1 NAR结构示意

如图1所示,Y(t)为网络的输入与输出,d为网络输入延时阶数,w为连接权重,b为阈值。

1.2 NAR神经网络参数确定

隐含层神经元个数和延时阶数是影响预测精度的关键参数,NAR神经网络的参数确定方法如下：

(1)隐含层神经元个数S由输入、输出层神经元个数L，H,以及常数a共同决定,其中常数a属于[0,10],表达见式(2)。

(2)

(2)输入、输出延时阶数d采用AIC准则确定,准则AIC由损失函数lnA,输入、输出阶数和d,预测数据序列长度N拟合运算形成,表达见式(3)。

AIC(d)=2d/N-2InA

(3)

当准则AIC函数值达最小时,NAR得最理想延时阶数d值[22]。

1.3 基于NAR邻近建筑位移预警

通过建立基于NAR神经网络的基坑开挖邻近建筑位移预测模型,对建筑稳定性进行预警。邻近地表变形与建筑变形具有连锁反应关系,地表的变形易引发建筑物变形,并且建筑物变形常具有一定时滞效应。本次建立的NAR神经网络预测模型,将与建筑监测点位移变化高相关性的地表监测竖向位移作为NAR网络模型的输入,将建筑监测点竖向位移值作为NAR网络模型输出,这样能够准确、及时判断建筑物的位移趋势,避免单以建筑物历史位移值预测下一时刻位移值的方式,误判基坑开挖深度增加导致位移突然加大或对基坑进行注浆加固位移突然减小等情况邻近建筑变形趋势,不能对建筑做好预防加固措施,从而导致人员经济损失。建立基于NAR网络的预警流程见图2。

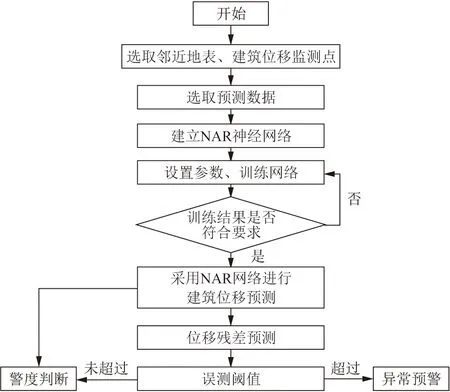
图2 基于NAR网络预警流程

由图2知,预测流程如下：

(1)综合考虑选取与建筑监测点位移变化高相关性邻近地表监测点位移值,预处理原始监测数据；

(2)建立由输入层、隐含层、输出层与输出延时层组成的基坑开挖邻近地表-建筑位移NAR神经网络。

(3)以地表位移变量作为输入，建筑位移变量作为输出,设置合理参数初始化，训练网络；采用自适应矩估计方法进行梯度下降迭代训练,不断更新权重和偏置矩阵；

(4)采用均方根误差RMSE、平均绝对误差MAE评价NAR网络预测效果,若误差控制在预设阈值内可结束训练,进行建筑位移值预测,否则重设参数进行训练；

(5)通过预测得到的建筑位移值与实际监测位移值取残差δ初步判断预测结果准确性,见式(4)。

(4)

式中：Wfre为预测值；Wact为实测值。

设定合理残差阈值能判断邻近建筑物位移是否异常,结合专家研究,设置预警误差阈值δ为10%。若未超过阈值,根据预测结果判断警度,及时采取相应措施。查找地铁设计规范、相关文献,结合地铁站工程实际情况确定地表、周边建筑沉降控制标准值见表1。

表1 监测控制标准 mm

参考海因里希的事故划分原则,将指标阈内各警度划分为4种,分别是重警、中警、轻警、无警。综合已有文献资料及工程实际设置警度值见表2。

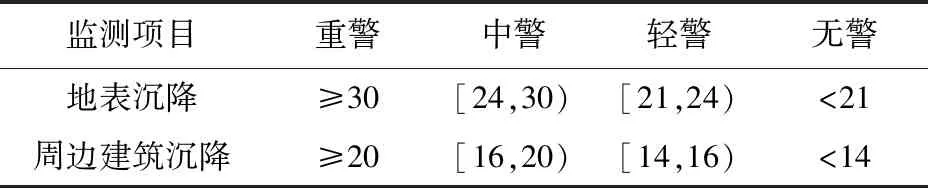
表2 预警值 mm

若超过阈值,进行异常预警,进一步分析异常原因。双线保证预警有效性,从而采取合理控制措施,为基坑邻近建筑保持稳定提供保障。

1.4 NAR神经网络评价指标

采用均方根误差RMSE、平均绝对误差MAE对模型预测能力进行定量评价,评价公式见式(5)，(6)。

(5)

(6)

式中：n为样本数；y为样本数据;yt为预测值。

通过均方根误差RMSE、平均绝对误差MAE值判断预测模型的拟合能力及泛化能力。

2 算例分析

以某明挖地铁站基坑开挖施工邻近地表位移和建筑位移监测数据为例进行分析研究,采用NAR神经网络建立地表-建筑位移预测模型,并与仅以建筑历史时刻位移值预测方式进行比较分析。

2.1 同步监测方案布置

建筑位于车站主体基坑西侧,为地上七层砖混结构建筑,浅基础,重要性分类为一般设施。该建筑位于车站西侧,距主体结构最近距离20.1 m,距离关系属接近。相邻基坑主要位于素填土、全风化板岩及中风化板岩,采用钻孔桩+内支撑支护。

图3 基坑-建筑位置

在实际工程中,为预测随着基坑开挖施工建筑沉降变化情况,利用相关性筛选后的邻近地表沉降数据对建筑沉降情况进行预测。根据该建筑现设监测点的位移数据,选取该建筑竖向位移监测点累计值最大的JGC035进行研究分析,该监测点位于建筑外墙转角处。以该监测点为中心,初步筛选合理影响范围内的地表沉降监测点：DBC1101，DBC1102，DBC1103，DBC1201，DBC1202，DBC1203，DBC1301，DBC1302，DBC1303进行相关性分析,该9个地表监测点延基坑等距布置,具体布置见图4。

图4 基坑-建筑监测点布置

2.2 地表-建筑位移相关性及预测数据选取

Spearman相关系数(记为P值)绝对值越大意味着相关性越强。正P值对应正相关,负P值表示负相关。其相关系数求解方法见式(7)：

(7)

式中：x为独立变量；y为依赖变量。

应用Spearman相关系数筛选相关性强的邻近地表沉降监测值为输入值,各地表监测变量与建筑转角监测点位移变化相关系数情况见图5。

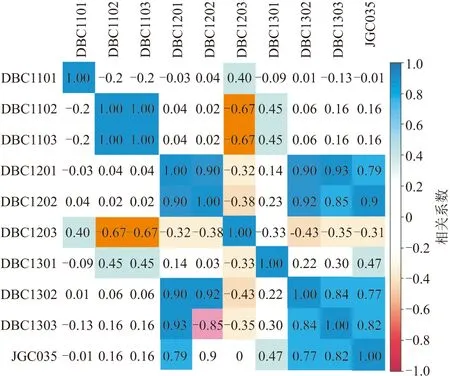
图5 不同监测点的相关系数

由图5知,与建筑物监测点JGC035相关性最强的地表监测点为DBC1202,两点呈显著非线性相关,相关系数为0.9。以两点监测位移数据进一步进行分析,其关系见图6。

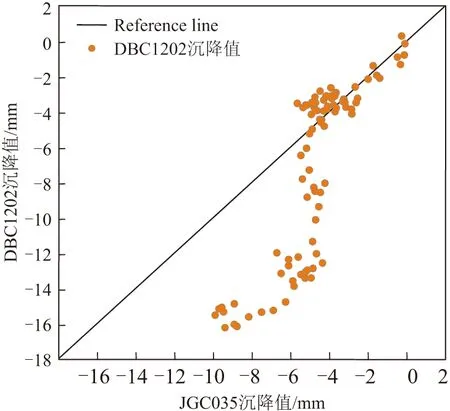
图6 DBC1202与JGC035相关性

由图6知,JGC035的竖向位移随地表竖向位移的增大而增大,具有相关性。以JGC035竖向位移为输入建立NAR模型进行建筑竖向位移预测模型研究。统计分析地表监测点DBC1202、建筑物监测点JGC035的竖向位移时程图,见图7。

图7 地表-建筑竖向位移时程曲线

由图7知,虽建筑位移与地表变化波动不完全一致,但整体趋势相似,并且地表竖向位移产生趋势变化的时间节点早于建筑竖向位移变化。

2.3 NAR参数设置及网络结构训练

构造的NAR神经网络包含2个输入层、1个隐藏层、1个输出层。根据式(2)，(3)确定神经网络参数。其中隐含层为包含12个神经元,输入与输出延时阶数为2。共采集到基坑开挖施工期间监测点竖向位移数据422个,将各序列数据75%划分为训练集，10%划分为验证集，15%划分为测试集。采用开环结构训练NAR网络,训练精度为10-3。NAR预测训练集、验证集、测试集的拟合优度见图8。

图8 拟合优度

由图8知,各数据集的拟合优度值R都在0.99以上,说明训练的NAR模型具有较高预测精度和适用性。进一步分析NAR网络的预测误差,自相关情况见图9。

图9 预测误差图自相关

预测相关系数值在延时阶数为0时最大,且在其他延时阶数不超过95%的置信区间为佳。由图9知,该训练后模型在0时达最大,其余均未超过置信区间,说明该训练后模型预测性能较好。NAR网络预测效果误差情况见图10。

由图10知,预测值与实测值相差不超过0.5,说明此NAR动态神经网络的预测精度较高。可以采用该网络模型对邻近建筑的竖向位移进行预测及进行警度判断。

图10 预测误差

2.4 预测结果分析

选取基坑开挖过程中监测点地表DBC1202、建筑JGC035产生的211 d竖向位移实测数据进行神经网络预测模型研究。以数据的75%进行模型训练,保存训练好的预测模型进行建筑位移预测。采用多步预测法,以前八天实测数据作为输入,其对应的目标输出为后一天的预测值,再将得到的预测值与其前七天共同作为输入。通过多步循环预测,能够得到未来八天的预测值,将预测值与实测值进行误差分析。采用NAR动态神经网络、BP前馈神经网络、LSTM长短期记忆神经网络建立地表-建筑、历史时刻两种方法的预测模型,预测值与实测值比较结果见表3。

表3 预测值与实测值比较 mm

采用均方根误差RMSE、平均绝对误差MSE对三种神经网络建立的地表-建筑模型、历史时刻模型的预测结果进行精度评定,预测精度值见表4。

表4 预测精度 mm

由表4知,对于地表-建筑和历史时刻两种预测方法,与BP，LSTM两种神经网络模型相比,NAR预测模型的RMSE和MAE均最低。表明NAR预测模型对于基坑开挖施工过程中,邻近建筑产生位移变化的动态时序问题,其预测模型具有更佳的拟合能力和更优良的泛化能力。

进一步分析NAR预测模型对于地表-建筑和历史时刻方法之间的精度差异。通过地表-建筑法预测的均方根误差和绝对误差较仅用建筑历史时刻数据预测法的误差值均小。通过地表-建筑预测的均方根误差为0.198,平均绝对误差为0.372,通过仅用历史时刻预测的均方根误差和平均绝对误差分别为0.693，0.787。

通过比较两种方法的误差(预测值与实测值的差值绝对值)确定更合适的邻近建筑位移预测方法,统计两种方法的误差范围及残差大小,对误差波动范围进行比较分析,见表5。

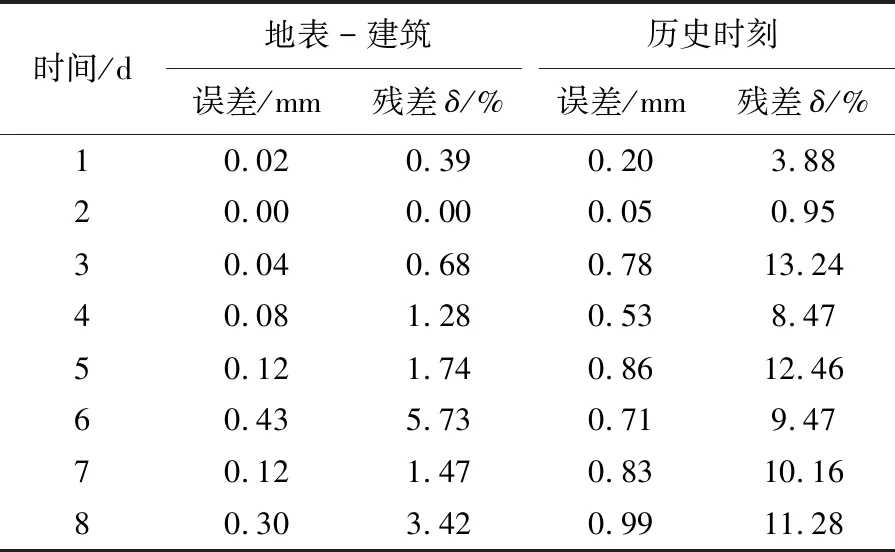
表5 预测误差值范围

地表-建筑法误差在0～0.43 mm区间,通过建筑历史时刻预测误差在0.05～0.99 mm区间。综合分析,NAR模型采用建筑-位移法预测误差波动更小,其预警结果与实际情况一致。地表-建筑法的残差δ在0.00%～5.73%之间,历史时刻法的残差δ在0.95%～12.46%之间,且4次超过预警阈值,发生异常预警。但在基坑开挖过程,预测期间的建筑位移变化处于无警状态,此时应用建筑位移历史时刻数据对其后期位移变形进行预测的结果预警出现误判现象。

为清晰对比NAR模型对两种预测方法的建筑竖向位移的预测性能,对各模型预测值与实测值进行比较分析,预测值与实测值对比见图11。

图11 预测误差图

由图11知,在建筑竖向位移趋势发生转变时段,地表-建筑法预测位移预测拟合效果更加优良,变化趋势转变迅速,模型适应性强。而仅通过历史时刻值预测变形的曲线变化趋势平缓,预测结果产生较大误差。这是由于神经网络以实测数据进行模型训练,对监测得到的历史数据的变化规律进行拟合,当基坑开挖过程中受基坑开挖施工、架设支撑、注浆加固等多种因素影响时,变形规律发生突然变化,对建筑位移变化规律的捕捉出现滞后性,产生预测误差,从而引起警度误判。

应用NAR以地表竖向位移来预测建筑竖向位移的效果展现更加明显的优势,同时表明NAR神经网络模型对施工中建筑竖向位移这类随时间动态波动的非线性数据具有更高的预测精度和适用性,更能满足工程需求。

3 结 论

基坑开挖过程中,紧邻建筑难免会受其影响发生变形,依据NAR神经网络建立地表-位移预测模型,能够避免邻近建筑位移的时滞性导致预测产生误差。能够根据预测结果准确判断建筑位移预警程度,从而采取合理有效措施。主要结论有：

(1)应用Spearman相关系数进行分析,选定建筑监测点紧邻地表监测点的位移值具有显著非线性相关性,相关系数值在0.79～0.90之间。对经过相关性筛选的地表监测点位移值与建筑位移值进行分析,虽建筑与地表位移变化波动不完全一致,但整体趋势相似,并且地表竖向位移产生趋势变化的时间节点早于建筑竖向位移变化。

(2)NAR动态神经网络能够准确预测非线性时序问题。在两种方法中,NAR的预测误差值均在0.5 mm以下,对于解决基坑开挖邻近建筑预测问题具有高精度和低误差的优势。

(3)在受基坑开挖影响,建筑沉降速率突然加大时,地表-建筑法预测位移预测拟合效果更加优良,变化趋势转变迅速,模型适应性强。而通过历史时刻值预测变形趋势平缓,出现较大误差,在预测过程中产生多次异常预警,影响预警程度判断。