基于MATLAB的小波去噪的研究
张 静,陶彬彬
基于MATLAB的小波去噪的研究
张 静,陶彬彬
(皖江工学院 电气信息工程学院,安徽 马鞍山 243031)
小波分析法去噪是当前广泛应用的信号去噪方法,为研究小波分析去噪效果,本文首先对小波分析的基本理论进行介绍,然后介绍了小波去噪原理,最后通过MATLAB对小波去噪效果及影响因素进行实验仿真。仿真结果通过波形、信噪比SNR和最小均方误差MSE进行分析。
小波去噪;小波基;阈值;小波包去噪;去噪效果
近些年来,小波分析理论发展得十分迅速,良好的时域和频域特性使得其广泛地被应用于实际。在现实中,搜集到的信号往往都是含有噪声的,噪声的存在常常会将原始信号所要表达的信息掩盖掉,所以,在实际对信号的处理过程中,降噪是首先要进行的,并且是非常重要的一个步骤。
小波分析法去噪是当前广泛应用的信号去噪方法,小波分析法源于傅里叶变换,却相比传统的傅里叶分析去噪而言,更适合于对非平稳信号的去噪问题。傅里叶分析去噪适合于平稳信号去噪,可是生活中非平稳信号是绝大部分的,因此使用傅里叶分析法来去噪就存在着局限性[1]。多分辨率分析是小波分析的特点,并且无论在时域还是频域内,均具有表征信号局部特征的能力[2]。因此,在去噪领域中,小波理论受到了广泛的关注,并取得了不错的效果[1-7]。
小波分析去噪的核心环节包括小波基函数的选择,阈值函数的选择、分解的层数等,小波包相对于小波分析对于高频的刻画更为精细,小波包去噪也被用于信号的去噪[8-11]。本文主要研究小波去噪,以及影响最终去噪效果的因素,并通过MATLAB进行仿真实验。去噪实验包括3部分:一是研究小波基选择、阈值选取、分解层数对小波分析去噪效果的影响,二是通过对非平稳信号去噪,比较小波去噪与傅里叶分析去噪的效果,三是小波包去噪效果的研究。
1 小波理论
1.1 小波变换


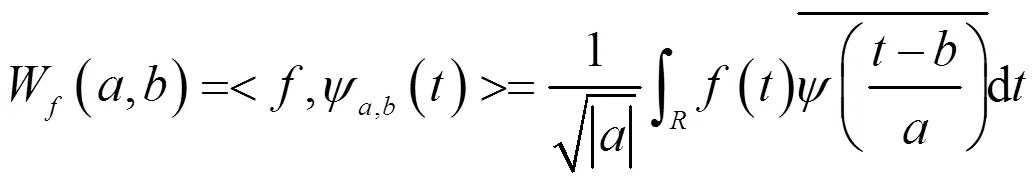
其重构公式(即小波逆变换)为:

1.2 几种常见的小波基
小波基选取是小波分析去噪的关键环节之一,选择合适的小波基作为小波分析的基函数,能够使小波去噪取得不错的效果。以下为几种常见的小波基函数。
(1)Haar小波系
Haar小波的定义为:
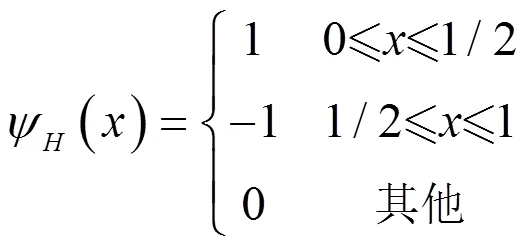

Haar小波系为A. Haar提出的一种正交的函数系,此小波系具备紧支撑性,并且在正交的函数系中是属于最简单的一种[12]。
(2)Daubechies(db)小波系
Daubechies(db)小波函数也是由Daubechies构造的小波函数,是从两尺度方程系数{h}出发而设计的离散正交小波函数[12]。简便起见,往往记作为db,为小波的阶数。db也为具备紧支撑正交特性的小波基系列,但是,db(≠1)不具备对称性的特征,也无显示表达式。但是,{h}的传递函数的模的平方却具备着显式表达式。
(3)SymletsA(sym)小波系
SymletsA函数为一种近似对称的,紧支集、双正交特性小波函数系,为db小波函数的一种改进,此SymletsA函数一般表示为sym的形式,其中=2,3,4,5,6,7,8[12]。
(4)Coiflet(coif)小波系
Coiflet小波基具有紧支撑正交特性,是由Daubechies构造的小波函数,函数有coif(=1,2,3,4,5)这一系列,Coiflet小波基比db小波基对称性更好,而且coif与db3、sym3具有相同的支撑长度,与db2、sym2具有相同的消失矩数目[12]。
虽然小波系有很多种,但是在小波分析中,对于小波基函数的选取并没有固定的准则,通常按照染噪信号的特征以及小波基函数本身的属性来进行选取[11]。
1.3 小波包理论
小波变换是一种将时域分析、频域分析联系在一起的分析方法,多分辨率分析法是将信号分解为高频部分和低频部分的分析方法,可是,通常是将低频部分保留下来,而对于高频部分的分析处理往往不知所措[13]。
小波包分析与小波分析相比,突出优势在于,不仅可以对低频部分进行分解,而且可以对高频部分也实施了分解,(如图1所示为3层小波包分解图),因此,局部分析能力更加精确。
2 小波去噪原理
2.1 小波分析去噪原理
小波去噪一般分为染噪信号的分解、阈值的处理、信号的重构3个步骤。
(1)信号的分解:选取小波基对染噪的信号进行小波变换。
(2)阈值的处理:事先设定一个阈值,然后将比设定阈值低的小波系数去掉,保留比设定阈值高的小波系数,从而可以将噪声去除,保留住有用信号的信息。
(3)信号的重构:用处理后的小波系数进行信号重构。
2.2 阈值去噪
模极大值法、空域相关法、小波阈值法是小波滤波去噪的3种主要的方法,相比较于前2种滤波方法,小波阈值法滤波具有算法简单、计算量小、滤波效果好等特点,对于信噪比低的信号的处理也比较适用[13],因此,关于小波阈值法信号滤波的研究及应用较为广泛[14-16]。
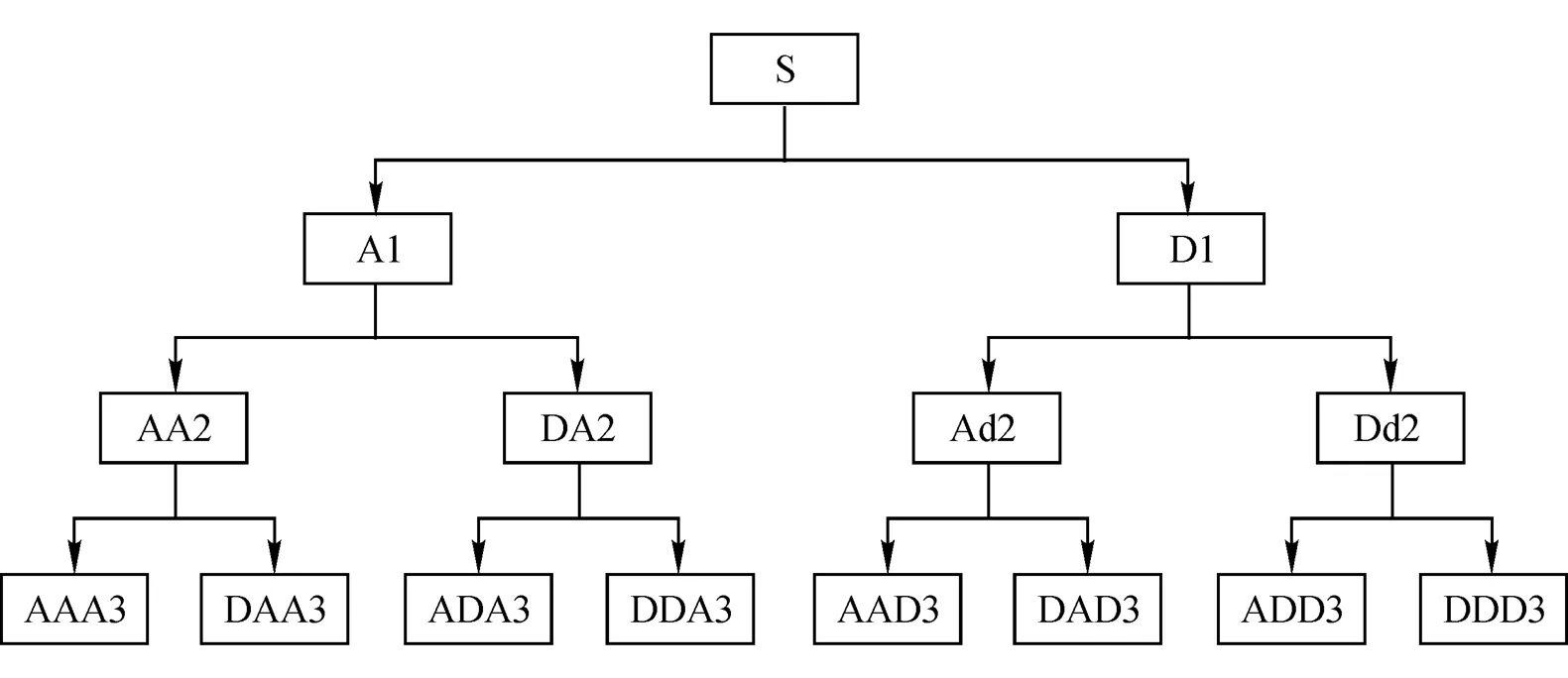
图1 3层小波包分解图
小波阈值去噪通常可以分为硬阈值去噪及软阈值去噪2种。
Donoho提出的硬阈值函数的数学表达式为:

软阈值的数学表达式为:

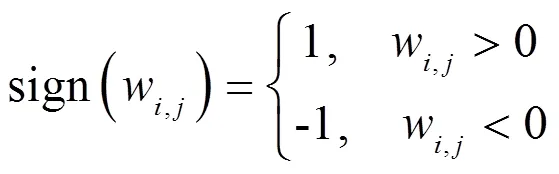
常见的阈值选择规则有以下4种:①固定阈值sqtwolog规则,阈值=2In();②启发式阈值Heursure规则,为最优预测变量阈值选择;③自适应阈值选择Rigruse规则,此种规则是基于无偏估计;④极大极小阈值Minmaxi规则,此规则也是一种固定的阈值选择规则[13]。其中,Rigruse、Minmaxi阈值选取规则在处理噪声时较为保守,仅将部分系数置零,而sqtwolog、Heursure阈值选取规则则将所有系数处理掉,前者可能会造成去噪不足,后者可能会造成有用信号的高频部分被当成噪声而去除掉[11]。
阈值函数以及阈值选取规则是最终对小波滤波去噪效果产生影响的关键性因素。
2.3 小波包去噪
与小波分析去噪相比,小波包对信号的分解以及重构愈加精细,对低频部分以及高频部分均实施分解,因而具有更强、更精确的局部分析能力[11]。
小波包阈值去噪的基本步骤如下:①对信号进行小波包分解;②选择最优小波基;③小波包分解系数的阈值化;④信号的小波包重构。
3 去噪实验仿真
3.1 不同小波基下信号去噪
本实验为仿真小波基函数选取、分解的层数、阈值选取对小波分析最终去噪效果的影响。如图2为原始信号以及加噪信号。
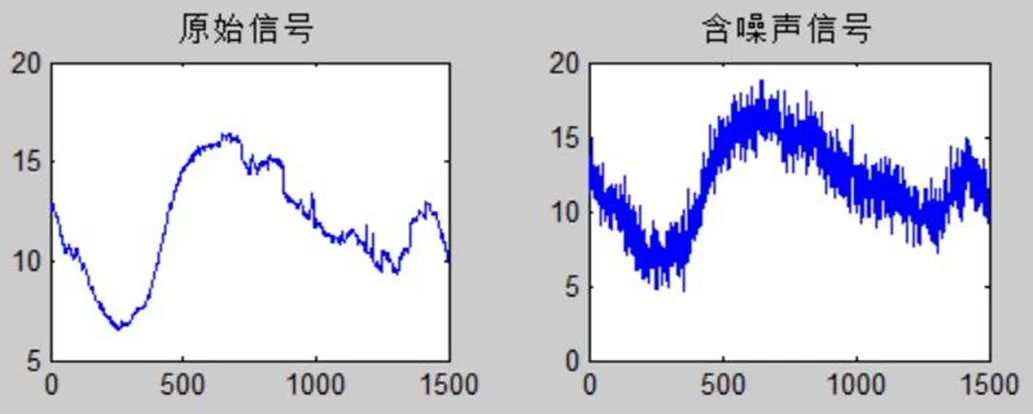
图2 原始信号及加噪信号

表1 3层分解的小波分析去噪
coif3sym5db4haar 软阈值MSE0.14190.13520.13120.1601 硬阈值MSE0.23750.23760.27100.2555 软阈值SNR30.130330.338830.471129.6059 硬阈值SNR27.893727.890727.320227.5752 加噪SNR21.440921.440921.440921.4409
表2 5层分解的小波分析去噪
coif3sym5db4haar 软阈值MSE0.05620.05760.05820.1155 硬阈值MSE0.15280.17050.19460.2143 软阈值SNR34.151934.047633.997331.0237 硬阈值SNR29.807629.334028.758128.3400 加噪SNR21.440921.440921.440921.4409
由表1、表2可得,同一种小波基下,5层分解与3层分解相比,具有更高的信噪比SNR,更低的最小均方根误差MSE。实验结果表明,分解的层数越多,去噪效果就越好,同时也增大了计算量。
通过表1和表2的数据,可以发现软阈值情况下,具有更高的信噪比SNR,更小最小均方误差MSE,说明噪声更小,去噪后的信号与原始信号更为接近。
通过4种小波基去噪结果的数据对比可以发现,coif3、sym5、db4 3种小波基情况下的滤波效果要好于haar小波基情况。coif3小波基、sym5小波基处理噪声效果比db4小波基略好。因此,小波基的选择不唯一,没有一种小波基对任何一种信号去噪都能取得最优的效果。所以,实际去噪时,应根据具体情况来选择适合的小波基函数对小波进行分解。
图3~图6分别为不同小波基情况下的去噪波形图,从中可以发现coif3、sym5、db4 3种小波基下的去噪效果要好于haar小波基情况。软阈值去噪效果好于硬阈值,去噪之后跟原信号更接近。但是haar小波基特更适合于连续性较差的信号的小波去噪,比如block信号。coif3、sym5更适合于连续性较好的信号的去噪,比如Doppler信号的去噪。
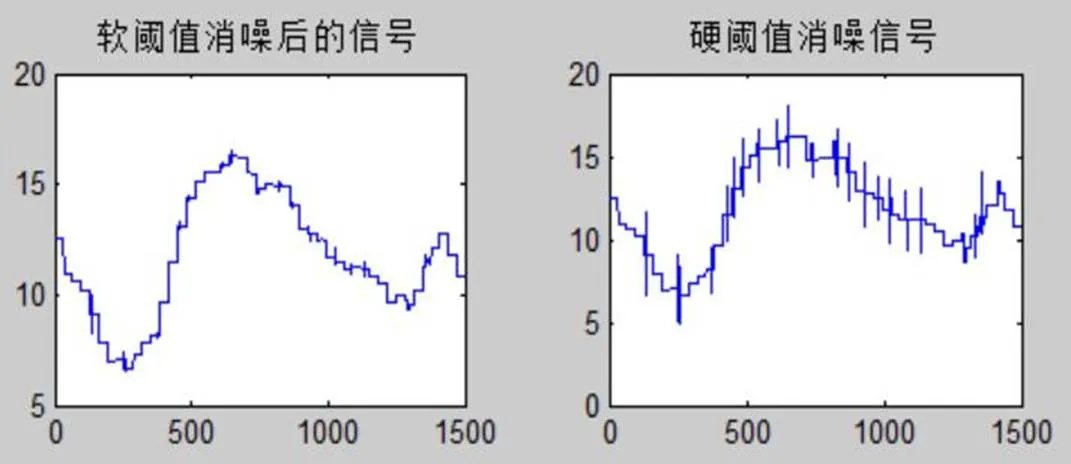
图3 haar小波基分解的小波去噪

图4 coif3小波基分解的小波去噪
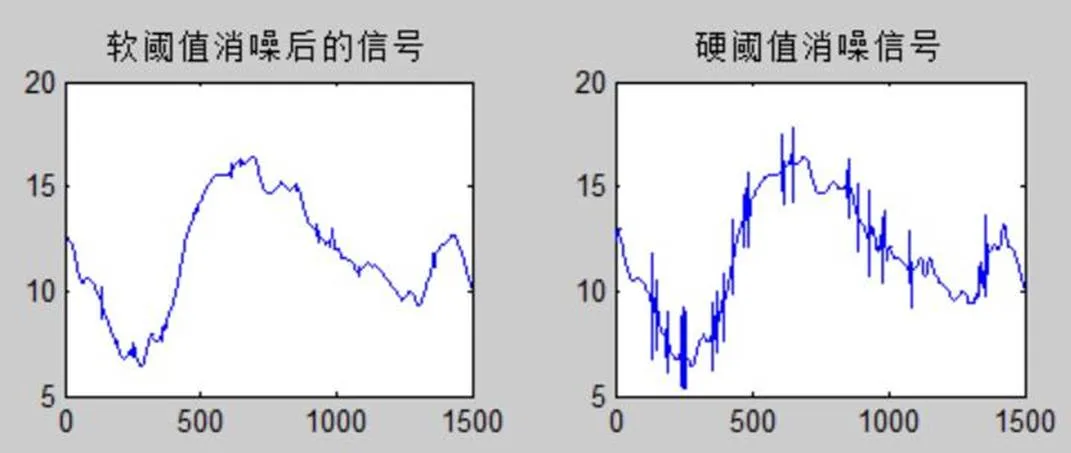
图5 sym5小波基分解的小波去噪
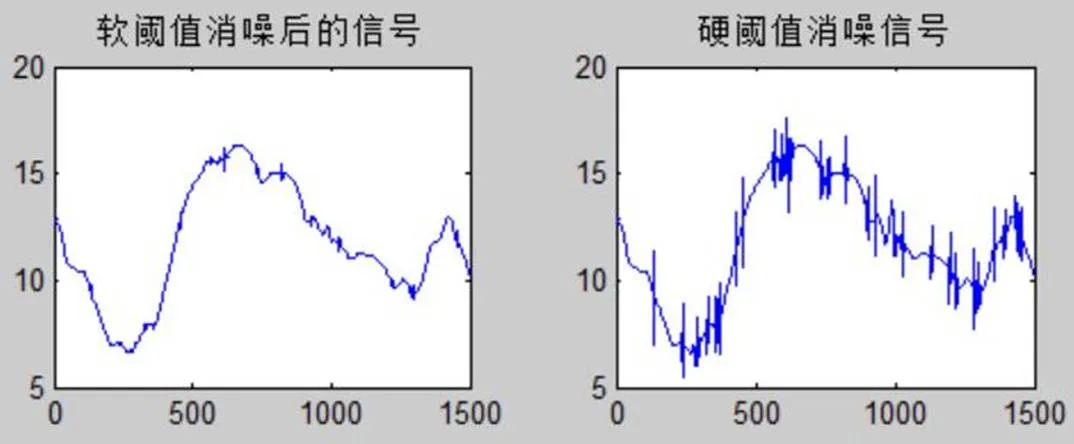
图6 db4小波基下的小波去噪
3.2 小波去噪与傅里叶分析去噪效果比较
首先,产生测试信号—Doppler信号,Doppler信号为一种非平稳信号,加入白噪声,得到原始信号和染噪信号如图7所示。然后通过小波分析和傅里叶分析分别对加噪的非平稳信号进行去噪。其中,小波分析法选取sym4小波基对加噪信号进行4层分解,阈值选择采用最优预测变量阈值heursure,软阈值去噪。
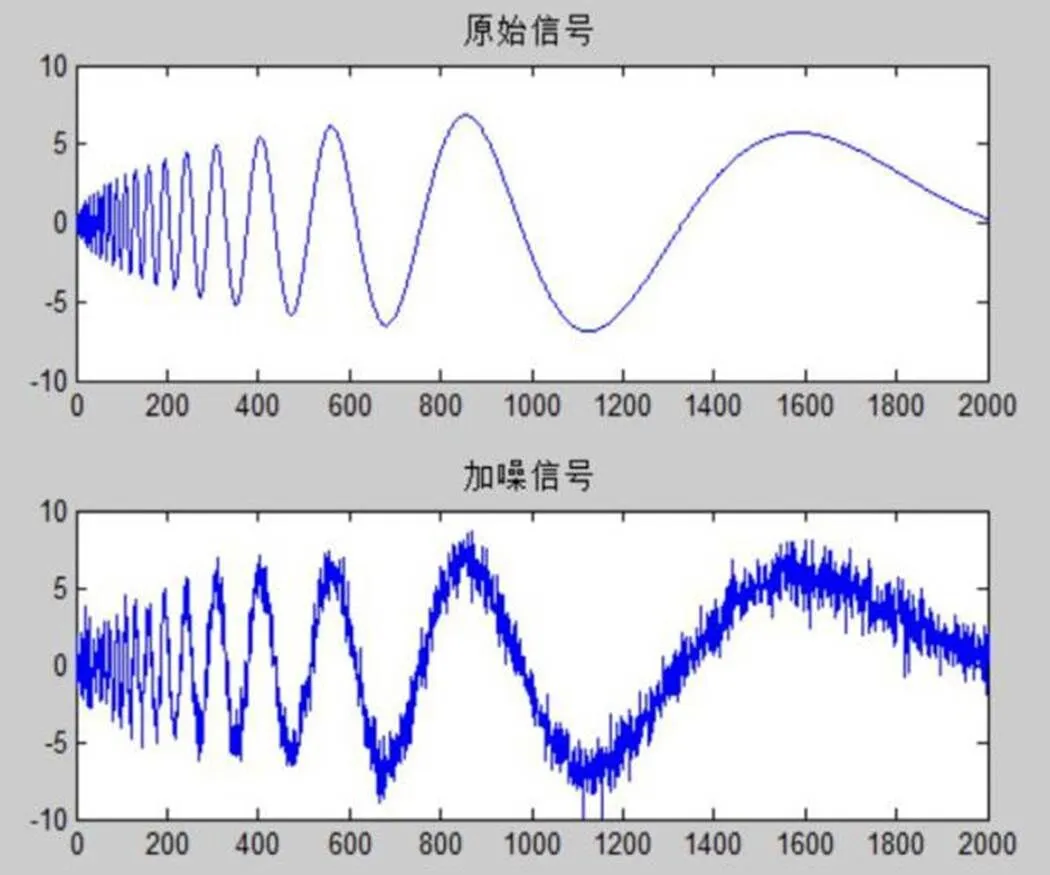
图7 原始信号及加噪信号
由图8可知小波分析去噪结果好于傅里叶分析去噪。在非平稳信号的去噪方面,小波分析去噪相对于傅里叶分析具有很大的优势,并且在实际工程应用中,大多数的信号也都为非平稳信号。
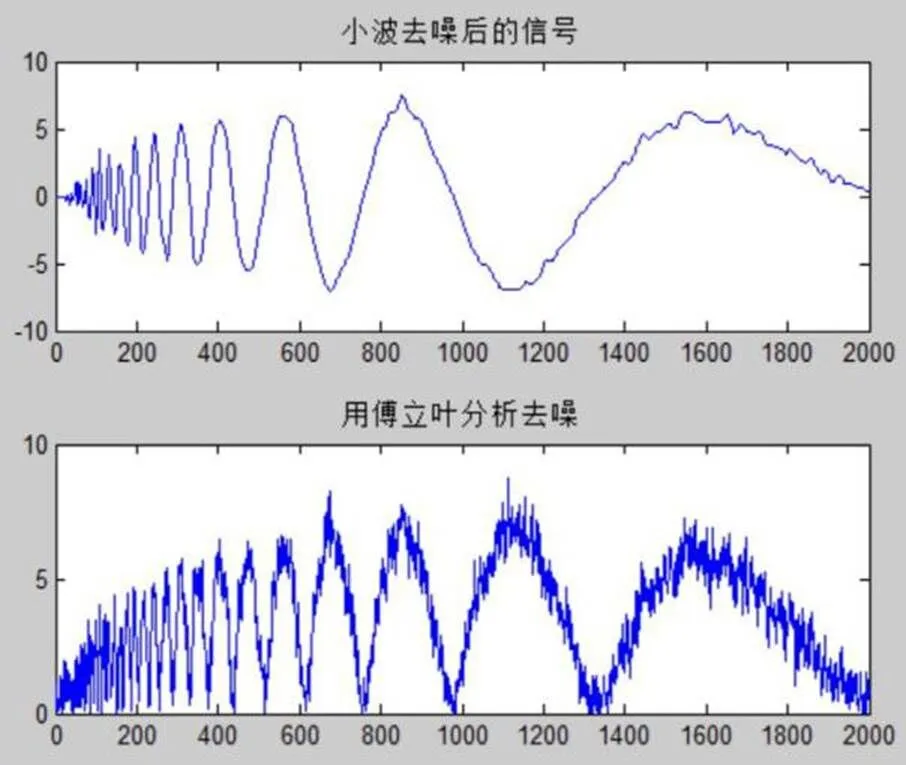
图8 小波去噪及傅里叶分析去噪比较
3.3 小波包去噪
3.3.1 分解层数对去噪效果的影响
先产生bumps测试信号,然后高斯白噪声加入bumps信号,得到原始信号及加噪信号如图9所示。然后运用小波包分析对染噪信号进行去噪处理,实验中,小波包分解层数分别设置为2层、4层、5层、8层,得到去噪后信号波形如图10所示。
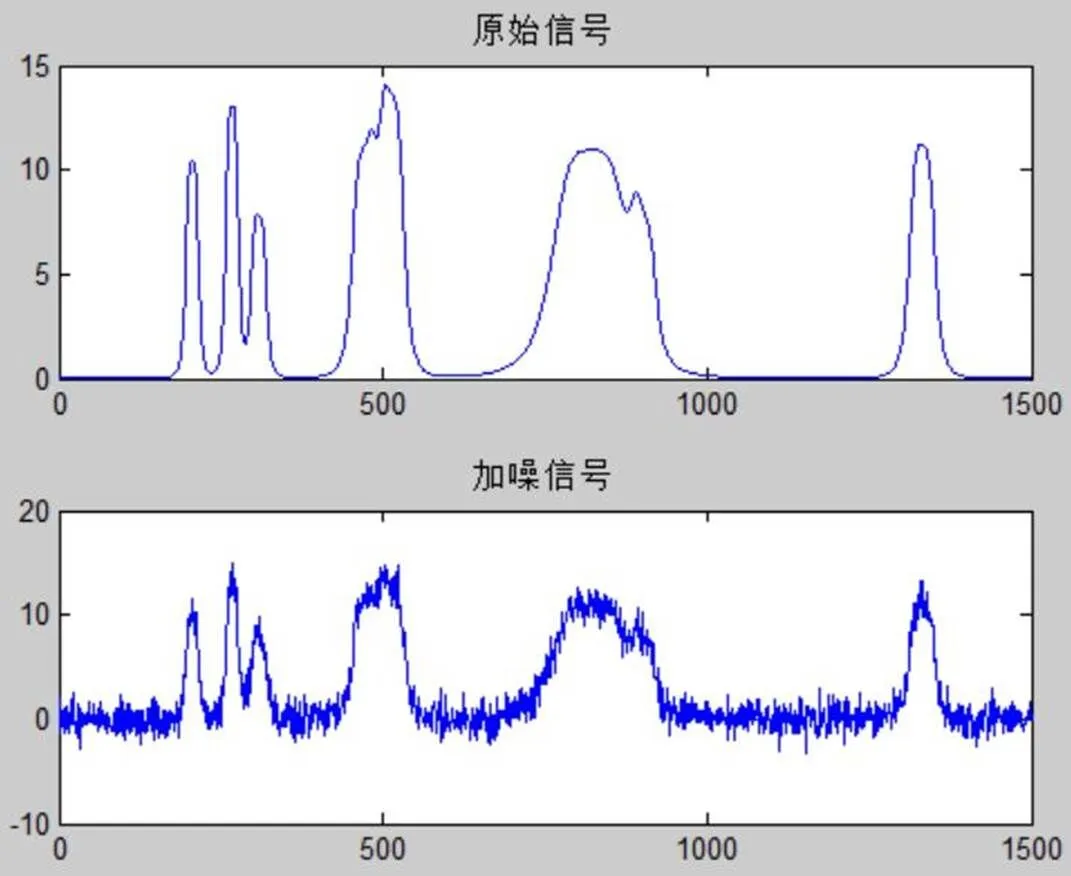
图9 bumps信号及加噪信号
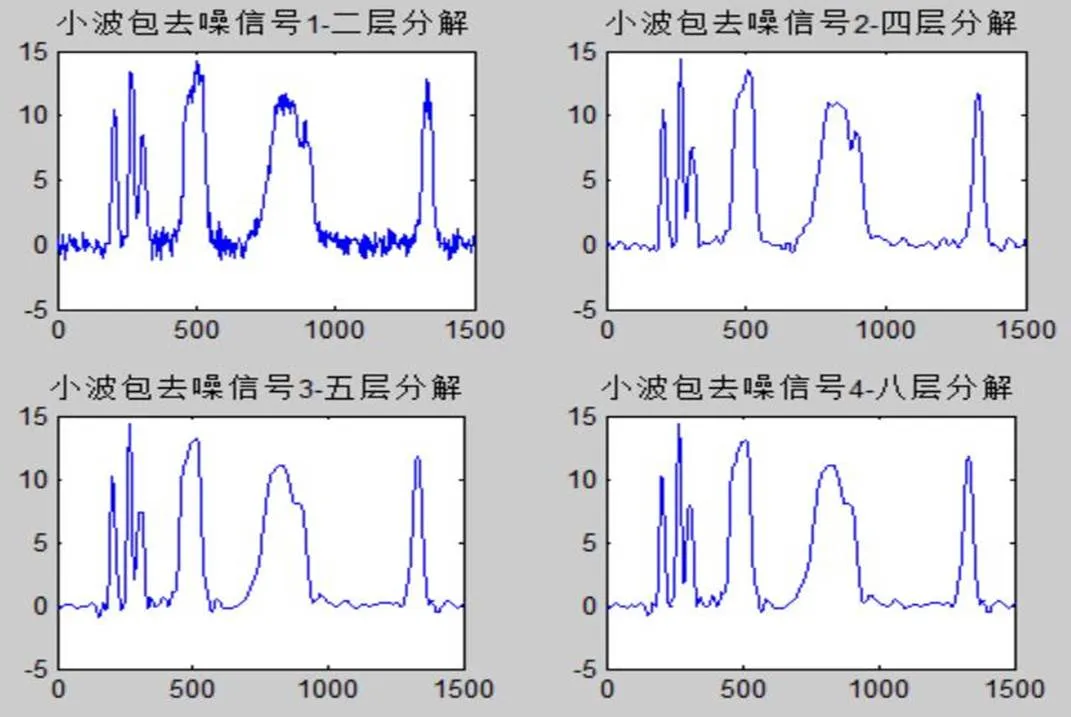
图10 不同分解层数的小波包去噪比较
从图10可以发现,分解的层数越多,信号的去噪效果就越好,但是,超过4层分解之后,去噪效果改善并不明显,而更高层的分解反而会增大计算量,因此,小波包分析去噪通常采用4层分解即可。
3.3.2 小波包与小波分析去噪比较
先产生quadchirp测试信号,然后将高斯白噪声加入quadchirp,得到原始信号及加噪信号的波形如图11所示。对加噪的quadchirp信号分别采用小波包和小波分析进行去噪处理。

图11 quadchirp信号及加噪信号
小波包去噪方法采用软阈值去噪,4层分解;小波分析去噪,阈值选择采用最优预测变量阈值heursure,分别采用软阈值和硬阈值2种方式,分解层数为4层。实验分别选用coif3、sym5、db4、haar 4种小波基作为小波分解的基函数。仿真结果如图12所示。

图12 小波包去噪与小波去噪比较
图12为小波包去噪与小波分析软阈值去噪以及小波硬阈值去噪比较。从图12可以发现,对于quadchirp信号而言,小波包去噪的效果明显好于小波去噪,因为小波包去噪更灵活,对低频部分和高频部分同时进行分解,局部分析能力更为精确。
表3为小波包去噪和小波去噪的结果数据,通过表3可以发现,小波包去噪相比较小波硬阈值去噪、小波软阈值去噪具有更高的信噪比SNR和更低的最小均方误差MSE,表明对于quadchirp信号而言,小波包去噪的效果要优于小波分析去噪。
表3 小波包去噪和小波去噪的比较
heursurecoif3sym5db4haar 软阈值MSE1.39811.64271.47958.5560 硬阈值MSE1.03871.07561.04287.5115 小波包MSE0.54090.56130.72221.7632 软阈值SNR10.52139.821010.27542.6539 硬阈值SNR11.811911.660111.79483.2194 小波包SNR14.645714.484513.38989.5135 染噪信号SNR12.154512.154512.154512.1545
仿真实验中原始信号的获取采用MATLAB中自带的小波去噪测试信号:信号Bumps、Doppler和Quad-chirp等,信号Block、Bumps、Heavysine、Doppler以及Quad-chirp,这些信号基本已经涵盖了地震、图像、光谱以及其他科学各领域中所涉及的信号特征[10]。
4 结束语
小波基、阈值、分解层数都影响着小波分析去噪的效果优劣,因此,根据实际情况选择适合小波基、分解层数、阈值可以提高去噪质量。在对于非平稳信号去噪方面,小波分析更适合。实际上,小波包去噪是一种更为精细的去噪方法,对于高频部分也能够细致地刻画,使得去噪后的信号更接近原始信号。
[1] 曹银萍. 基于MATLAB的小波分析在信号去噪中的应用[J]. 信息记录材料, 2018, 19(7): 85-87.
[2] 王勇, 王梨英, 魏丽娟, 等. 基于db4小波基阈值的GPR信号去噪尺度分析[J]. 数学的实践与认知, 2018, 42(22): 114-119.
[3] 朱文斌, 雷秉山, 雷志勇. 基于小波变换的红外探测系统信号去噪[J]. 红外技术, 2018, 40(11): 1047-1051.
[4] 杨敬松, 王晗, 姚振静. 一种小波综合阈值地震信号降噪方法[J]. 震灾防御技术, 2018, 13(2): 439-446.
[5] 史荣珍. 不同小波基函数下的语音信号去噪研究[J]. 现代电子技术, 2014, 37(3): 49-51.
[6] 黄娇, 袁正午, 田增山. 一种小波阈值函数的CDMA信号去噪研究[J]. 电视技术, 2013, 37(7): 75-78.
[7] 曾敬枫. 基于MATLAB不同小波基的小波阈值图像去噪算法[J]. 智能计算机与应用, 2016, 6(4): 75-77.
[8] 胡明宇, 王先培, 肖伟. 基于UHF的局部放电信号小波包去噪与模式识别研究[J]. 仪表技术与传感, 2016, (7): 93-96.
[9] 沈鑫, 束洪春, 曹敏, 等. 基于奇异值的小波包去噪研究[J]. 电测与仪表, 2018, 55(15): 1-3.
[10] 王志斌, 曹红伟, 刘佳佳. 基于小波包去噪与EMD的故障电弧检测算法研究[J]. 电测与仪表, 2019, 56(6): 117-121.
[11] 冯安安, 岳建海, 郑义, 等. 思维进化算法优化小波包去噪仿真分析[J]. 计算机仿真, 2020, (7): 285-290.
[12] 沈再阳. MATLAB信号处理[M]. 北京: 清华大学出版社, 2019: 318-319.
[13] 孔玲军. MATLAB小波分析超级学习手册[M]. 北京: 人民邮电出版社, 2014: 235-304.
[14] 刘霞, 潘洪屏, 高晓春, 等. 基于小波阈值的地震信号去噪处理[J]. 科学技术与工程, 2010, 10(29): 7251-7254.
[15] 曾亮, 刘祖润. 一种新的小波阈值去噪算法及仿真[J]. 青岛科技大学学报: 自然科学版, 2014, 35(1): 67-72.
[16] 赵银善. 一种改进的小波阈值函数去噪方法[J]. 计算机工程与应用, 2013, 46(1): 212-214.
Research on Wavelet Denoising Based on MATLAB
ZHANG Jing, TAO Bin-bin
(School of Electrical and Information Engineering, Wanjiang University of Technology, Ma'anshan 243031, China)
Wavelet analysis denoising is a widely used signal denoising method at present. In order to study the denoising effect of wavelet analysis, this paper first introduces the basic theory of wavelet analysis, then introduces the principle of wavelet denoising, and finally carries out experimental simulation on the effect and influencing factors of wavelet denoising through MATLAB. The simulation results were analyzed by waveform, SNR and MSE.
wavelet denoising; wavelet basis; threshold; wavelet packet denoising; denoising effect
10.15916/j.issn1674-3261.2022.03.008
TP391
A
1674-3261(2022)03-0177-06
2021-03-17
张静(1984-),女,江苏徐州人,副教授,硕士。
责任编辑:孙 林

